Regularization property of linear interference cancellation detectors

Abstract

In this article, we unveil a new property of linear interference cancellation detectors. Particularly, we focus in this study on the linear parallel interference cancellation (LPIC) detector and show that it exhibits a semi-convergence property. The roots of the semi-convergence behavior of the LPIC detector are clarified and the necessary conditions for its occurrence are determined. In addition, we show that the LPIC detector is in fact a regularization scheme and that the stage index and the weighting factor are the regularization parameters. Consequently, a stopping criterion based on the Morozov discrepancy rule is investigated and tested. Simulation results are presented to support our theoretical findings.

Introduction

Multi access interference (MAI) is the main limiting factor for the capacity of the third generation cellular system employing Code Division Multiple Access (CDMA) scheme [1]. Similarly, MAI is also limiting the capacity of optical networks using optical CDMA (OCDMA) technology. Other types of interference exist in other systems and may reduce capacity if not mitigated properly, i.e., the inter-carrier interference (ICI) in orthogonal frequency division multiple access (OFDMA) and inter-antenna interference (IAI) in multi input multi output (MIMO) systems, just to name a few [1].

The effect of interference on wireless systems such as 4G and beyond is expected to be more severe due to the fact that the cells are expected to become more condensed (i.e.,femto-cells) and the dimension of wireless technologies keeps increasing from one generation to another. For example, large MIMO systems with tens to hundreds of transmit/receive antennas are proposed for 4G and beyond in order to achieve high spectral efficiencies [2, 3]. To combat these different types of interferences, multiuser detectors (MUDs) have been developed [1]. MUDs are used mainly to reduce the effect of interference in wireless/wired systems and hence to increase system capacity and throughput. A large variety of MUDs was developed in the literature [1]. Typically, they range from simple but poor performance MUDs to complex but excellent performance MUDs. The challenge is usually to devise MUDs that tradeoff between low complexity and good performance. Applications of MUDs are diverse and in fact they have been applied to various wireless/wired systems such as MIMO-OFDM, SFBC-OFDM, OCDMA, just to name a few [4–6].

The decorrelating and the linear minimum mean square error (LMMSE) detectors are effective MUDs to eliminate MAI. They are also important for nonlinear multistage detectors (decorrelating decision feedback detector, LMMSE decision feedback detector, etc.) because the latter usually take their initial estimates from the decorrelator/LMMSE detector. Hence, reducing the computational complexity of the decorrelator/LMMSE detector reduces the total computational complexity of these nonlinear multistage detectors.

One constraint that limits the implementation of the decorrelator/LMMSE detector is its computational complexity which is in the order of O(N³) [1], where N is the dimension of the system’s cross-correlation matrix. For example, N in mobile WIMAX (IEEE 802.16Wireless MAN standard) [7] can reach up to 2048,and therefore to implement the decorrelator or the LMMSE detector, an inversion of a 2048-by-2048 system’s cross-correlation matrix is needed which imposes real challenges for its practical implementation. To overcome this problem, linear interference cancellation (IC) structures such as the linear successive interference cancellation (LSIC) and the linear parallel interference cancellation (LPIC) detectors, are introduced to approximate the decorrelator/LMMSE detector but with much less computational complexity O(N²) [8–10].

An important phenomenon that was noticed in the literature of linear IC detectors is their semi-convergence behavior, i.e., the best Bit Error Rate (BER) is obtained prior to convergence. This phenomenon was noticed first in [11–15], and recently in [16], and it seems to be a common feature in most linear IC’s if some conditions are met. However, no study has been yet carried out to explain the roots of this phenomenon and to devise necessary conditions for its occurrence. This study is needed to facilitate the development of appropriate stopping rules for terminating the linear IC detector’s iterations at the best BER performance before noise enhancement gets pronounced due to convergence to the decorrelator detector’s solution.

The contributions of this study are twofold: first we explain the rationale behind the semi-convergence behavior of the LPIC detector and derive necessary conditions for the occurrence of such a behavior. Specifically, we show that the LPIC detector exhibits a spectral filtering property where it attenuates solution components pertaining to small singular values of the system matrix and retains solution components pertaining to large singular values of the system matrix. Second, we exploit this property for the purpose of avoiding noise enhancement by early stopping the LPIC detector’s iterations. Towards that objective, we investigate a stopping rule based on the Morozov discrepancy principle [17]. The effectiveness of the proposed stopping rule is examined and extensively tested through simulations.

This article is organized as follows: in Section 2, the system model used in this study is briefly described. In Section 3, the naïve solution is analyzed and the common approaches used to overcome the effect of noise enhancement are detailed. Section 4 describes the structure of the LPIC detector, presents the proof for its spectral filtering property, analyzes its semi-convergence behavior and finally details the Morozov discrepancy rule for early stopping of its iterations. Finally, Section 5 supports the theoretical findings by a number of simulations and Section 6 concludes the article with some recommendations and possible future extensions of this study.

Notations

Throughout this article, the following notations are used.

•  ∘ denotes the Schur product.

•  ⊗ denotes the Kronecker product.

•  ${\mathbf{1}}_N$ denotes a 1-by-N vector of ones.

•  diag. denotes the diagonal operator.

•  ${.}^T$ denotes the transpose operator.

•  ${.}^H$ denotes the hermitian operator.

•  ${‖.‖}_2$ denotes the norm-2 operator.

•  |.| denotes the absolute value.

•  ${.}^{†}$ denotes the pseudo inverse.

•  lim. denotes the limit operator.

•  tr. denotes the trace operator.

•  max. denotes the maximum operator.

System model

A generic communication system is expressed in vector–matrix form as

$$\mathbf{r}\left(m\right)=\tilde{\tilde{\Psi }}\left(m\right)\mathbf{b}\left(m\right)+\mathbf{n}\left(m\right)$$

(1)

where r is the received signal vector and $\widetilde{\tilde{\mathbf{\Psi }}}$ is the system matrix and b is the vector of transmitted data symbols, and finally n is the vector of independently and identicallydistributed additive white Gaussian noise (AWGN) samples with zero-mean and variance ρ².

The system matrix $\widetilde{\tilde{\mathbf{\Psi }}}$ differs from one communication system to another, i.e., in a CDMA system it represents the matrix of the spreading codes whereas in a MIMO-OFDM system, the matrix $\widetilde{\tilde{\mathbf{\Psi }}}$ is in fact a combination of two matrices: the matrix of channel coefficients and the matrix of orthogonal IFFT subcarriers.

For illustration purposes, we consider the LPIC detector in the context of mitigating the ICI due to the misalignment of the carrier frequencies and the Doppler shifts of different users in an OFDMA system. Specifically, we consider a scenario of an uplink OFDMA system where K users transmit simultaneously over a synchronous Rayleigh fading channel using Quadrature Phase Shift Keying. We consider in this study the effect of ICI due to the misalignment of the carrier frequencies and the Doppler shifts of different users and we neglect the effect of ICI due to inter-symbol interference and inter-block interference. This is justified by assuming a flat fading channel for each subcarrier of each user and assuming that the users transmit synchronously; therefore, it is reasonable to omit the cyclic prefix operation. This is illustrated in Figure 1.

Figure 1

Typical uplink OFDMA channel.

Two main subcarrier allocation schemes are commonly used in the literature. In the first one, known as the block subcarrier allocation scheme, each user is assigned a block of adjacent subcarriers whereas in the second one, known as interleaved subcarrier allocation scheme, the total subcarriers are uniformly interleaved across all users. In this study, and since we are dealing with ICI, we consider the interleaved subcarrier allocation scheme because it is well known that this scheme suffers more from ICI compared to the block subcarrier allocation scheme [18].

An OFDM symbol consisting of N _u samples with sampling time T _u where N _u is the total number of data samples is transmitted using N orthogonal subcarriers. Without loss of generality, we assume that the total number of subcarriers of the IFFT matrix Ψ with elements ${\mathbf{\Psi }}_{n_u,n}=\frac{1}{\sqrt{N_u}}{e}^{\frac{j2\pi n_{u}n}{N_u}}$, 1 ≤ n _u  ≤ N _u and 1 ≤ n ≤ N is divided equally among all users; therefore, the total number of subcarriers per user is N _k  = N/K.

The received signal is expressed in vector–matrix form as

$$\begin{array}{ll}\mathbf{r}\left(m\right)& =\tilde{\mathbf{\Psi }}H\left(m\right)\mathbf{A}\mathbf{b}\left(m\right)+\mathbf{n}\left(m\right)\\ =\widetilde{\tilde{\mathbf{\Psi }}}\left(m\right)\mathbf{b}\left(m\right)+\mathbf{n}\left(m\right)\text{,}\end{array}$$

(2)

where$\tilde{\mathbf{\Psi }}$ isa combination of the IFFT and normalized carrier frequency offset (NCFO) matrices as follows: $\tilde{\mathbf{\Psi }}=\mathbf{\Psi }\circ \left({\mathbf{1}}_{N_k}\otimes \mathbf{{\rm E}}\right)$ where Ε is the NCFO matrix. The NCFO matrix is obtained as $\mathbf{{\rm E}}=\left[\begin{array}{cccc}\hfill {\mathbf{\varepsilon }}_1\hfill & \hfill {\mathbf{\varepsilon }}_2\hfill & \hfill \cdots \hfill & \hfill \begin{array}{cc}\hfill {\mathbf{\varepsilon }}_k\hfill & \hfill \begin{array}{cc}\hfill \cdots \hfill & \hfill {\mathbf{\varepsilon }}_K\hfill \end{array}\hfill \end{array}\hfill \end{array}\right]$where ${\mathbf{\varepsilon }}_k$ is given by ${\mathbf{\varepsilon }}_k={\left[\begin{array}{cccc}\hfill e^{\frac{j2\pi {\varepsilon }_k}{N_u}}\hfill & \hfill e^{\frac{j2\pi 2{\varepsilon }_k}{N_u}}\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill e^{\frac{j2\pi n_u{\varepsilon }_k}{N_u}}\hfill & \hfill \cdots \hfill & \hfill e^{\frac{j2\pi N_u{\varepsilon }_k}{N_u}}\hfill \end{array}\hfill \end{array}\right]}^T$ and ɛ _k is the NCFO of user k obtained as ${\varepsilon }_k=\Delta f_k/\mathit{\Delta f}$ where $\mathit{\Delta f}$is the subcarrier spacing. H(m) is the matrix of Rayleigh fading coefficients at the m thOFDM symbol where 1 < m < M, and it is given by$\mathbf{H}\left(m\right)=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\begin{array}{cccc}\hfill {\mathbf{H}}_1\left(m\right)\hfill & \hfill {\mathbf{H}}_2\left(m\right)\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill {\mathbf{H}}_{n_k}\left(m\right)\hfill & \hfill \cdots \hfill & \hfill {\mathbf{H}}_{N_k}\left(m\right)\hfill \end{array}\hfill \end{array}\right)$ where ${\mathbf{H}}_{n_k}\left(m\right)=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\begin{array}{cccc}\hfill h_{1,n_k}\left(m\right)\hfill & \hfill h_{2,n_k}\left(m\right)\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill h_{k,n_k}\left(m\right)\hfill & \hfill \cdots \hfill & \hfill h_{K,n_k}\left(m\right)\hfill \end{array}\hfill \end{array}\right)$. Channel fading coefficients are obtained in practice through channel estimation. Without loss of generality, we assume throughout this article perfect knowledge of the channel state information. A is the power weighting matrix and it is used to scale the signals of different users with different powers to simulate near–far scenarios. It can be even used to weight the subcarriers of the same user differently if needed. This matrix is given by $\mathbf{A}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\begin{array}{cccc}\hfill {\mathbf{A}}_1\hfill & \hfill {\mathbf{A}}_2\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill {\mathbf{A}}_{n_k}\hfill & \hfill \cdots \hfill & \hfill {\mathbf{A}}_{N_k}\hfill \end{array}\hfill \end{array}\right)$where${\mathbf{A}}_{n_k}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\begin{array}{cccc}\hfill a_{1,n_k}\hfill & \hfill a_{2,n_k}\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill a_{k,n_k}\hfill & \hfill \cdots \hfill & \hfill a_{K,n_k}\hfill \end{array}\hfill \end{array}\right)$.b(m) is the vector of transmitted symbols and it is formed as $\mathbf{b}\left(m\right)={\left[\begin{array}{cccc}\hfill {\mathbf{b}}_1\left(m\right)\hfill & \hfill {\mathbf{b}}_2\left(m\right)\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill {\mathbf{b}}_{n_k}\left(m\right)\hfill & \hfill \cdots \hfill & \hfill {\mathbf{b}}_{N_k}\left(m\right)\hfill \end{array}\hfill \end{array}\right]}^T$ where ${\mathbf{b}}_k\left(m\right)=\left[\begin{array}{cccc}\hfill b_{1,n_k}\left(m\right)\hfill & \hfill b_{2,n_k}\left(m\right)\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill b_{k,n_k}\left(m\right)\hfill & \hfill \cdots \hfill & \hfill b_{K,n_k}\left(m\right)\hfill \end{array}\hfill \end{array}\right]$. n(m) is an N-length vector of independently and identically distributed additive white Gaussian distributed samples with zero-mean and variance ρ²,and finally $\widetilde{\tilde{\mathbf{\Psi }}}\left(m\right)=\tilde{\mathbf{\Psi }}H\left(m\right)\mathbf{A}$ is a combination of the IFFT, the NCFO, the channel gain and power weighting matrices, respectively. This matrix can be decomposed as $\widetilde{\tilde{\mathbf{\Psi }}}\left(m\right)=\left[\begin{array}{cccc}\hfill {\widetilde{\tilde{\mathbf{\Psi }}}}_1\left(m\right)\hfill & \hfill {\widetilde{\tilde{\mathbf{\Psi }}}}_2\left(m\right)\hfill & \hfill \cdots \hfill & \hfill \begin{array}{ccc}\hfill {\widetilde{\tilde{\mathbf{\Psi }}}}_n\left(m\right)\hfill & \hfill \cdots \hfill & \hfill {\widetilde{\tilde{\mathbf{\Psi }}}}_N\left(m\right)\hfill \end{array}\hfill \end{array}\right]$ where ${\widetilde{\tilde{\mathbf{\Psi }}}}_n\left(m\right)$ is the n th column of the matrix $\widetilde{\tilde{\mathbf{\Psi }}}\left(m\right)$. For simplicity and conciseness we drop the OFDM symbol index m in all subsequent equations.

The naïve solution and the noise enhancement effect

The naïve solution or the decorrelator detector (sometimes known also as the zero forcing detector) is one of the basic detectors that completely eliminates the interference and it can be formulated as a least square minimization problem:

$$\underset{\mathbf{b}\in {ℂ}^K}{min}{‖\mathbf{r}-\widetilde{\tilde{\mathbf{\Psi }}}b‖}_2^2$$

(3)

The solution to this optimization problem is the decorrelator detector’s solution and it is given by

$${\mathbf{y}}^{\mathit{D}\mathit{E}\mathit{C}}={\widetilde{\tilde{\mathbf{\Psi }}}}^{†}\mathbf{r}\text{=}{\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{-1}{\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}$$

(4)

The naïve solution for ill-conditioned systems tends to amplify noise. To get more insight let us examine the singular value decomposition (SVD) of the decorrelator detector’s solution. Using the SVD, the system matrix $\widetilde{\tilde{\mathbf{\Psi }}}$ can be factorized as

$$\widetilde{\tilde{\mathbf{\Psi }}}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^H$$

(5)

where U and V are both the N-by-N unitary matrices, respectively, and Σ is an N-by-N diagonal matrix with elements ${\sigma }_n$, 1 ≤ n ≤ N. The N columns of U represent the left singular vectors of $\widetilde{\tilde{\mathbf{\Psi }}}$ and the N columns of V represent the right singular vectors of $\widetilde{\tilde{\mathbf{\Psi }}}$ and the N diagonal entries of Σ represent the singular values of $\widetilde{\tilde{\mathbf{\Psi }}}$. We assume without loss of generality that the singular values are ordered from the largest to the smallest with indices ranging from 1 to N. Consequently, the decorrelator detector’s solution can be written in terms of the SVD of $\widetilde{\tilde{\mathbf{\Psi }}}$ as

$${\mathbf{y}}^{\mathit{D}\mathit{E}\mathit{C}}={\widetilde{\tilde{\mathbf{\Psi }}}}^{†}\mathbf{r}=\mathbf{V}{\mathbf{\Sigma }}^{-1}{\mathbf{U}}^H\mathbf{r}=\sum _{n=1}^N\frac{{\mathbf{u}}_n^H\mathbf{r}}{{\sigma }_n}{\mathbf{v}}_n$$

(6)

and its norm is given by

$${‖{\mathbf{y}}^{\mathit{D}\mathit{E}\mathit{C}}‖}_2=\sqrt{{\sum }_{n=1}^N{\left(\frac{{\mathbf{u}}_n^H\mathbf{r}}{{\sigma }_n}\right)}^2}$$

(7)

As it can be seen from the equation above, the norm of y^DEC will not be too large as long as $\left|{\mathbf{u}}_n^H\mathbf{r}\right|<{\sigma }_n$ for large n. This is known as the discrete Picard condition [19].

Discrete picard condition

A meaningful solution is obtained if the Fourier coefficients ${\mathbf{u}}_n^H\mathbf{r}$ decay to zero on average faster than the singular values ${\sigma }_n$.

It can be seen that if the discrete Picard condition is not satisfied, the decorrelator’s solution goes unbounded. This is specifically true for ill-conditioned system matrices that tend to have many small singular values near zero. Moreover, since the noise tends to reside in the space spanned by singular vectors corresponding to singular values that are equal or less than the noise level, then noise components corresponding to singular values not satisfying the discrete Picard condition are magnified and consequently result in the noise enhancement effect observed in the decorrelator detector’s solution.

A typical scenario where an OFDMA system matrix gets ill-conditioned is the case of large frequency offsets. To illustrate this, the singular values of a system matrix with 128 subcarriers and 64 users are plotted in Figure 2. It can be seen that due to large values of the NCFO, many singular values are close to zero and therefore, for these singular values, there is a large chance that the discrete Picard condition will not be satisfied. This is illustrated in Figure 2 where the singular values, Fourier coefficients, and their ratio are plotted.

Figure 2

Discrete Picard condition for N = 128, K = 64, SNR = 10, and NCFO randomly generated from a uniform distribution between –0.5 and 0.5.

By virtue of Figure 2, it is evident that the norm of the decorrelator’s solution gets amplified if the singular values are below a certain threshold [19] (<0.7 in our case). All singular values below this threshold do not satisfy the discrete Picard condition and therefore contribute to the noise enhancement effect.

To combat this phenomenon, several regularization techniques have been developed. The main idea behind regularization is to filter out solution components pertaining to small singular values, that is

$${\mathbf{y}}^{\mathtt{R}\mathtt{E}\mathtt{G}}={\sum }_{n=1}^N{f}_n\frac{{\mathbf{u}}_n^H\mathbf{r}}{{\sigma }_n}{\mathbf{v}}_n=\mathbf{V}\mathbf{F}{\mathbf{\Sigma }}^{-1}{\mathbf{U}}^H\mathbf{r}$$

(8)

where F is an N-by-N diagonal matrix with elements $f_n$, known as filtering factors and should satisfy

$$f_n\simeq \{\begin{array}{l}1\text{if}{\sigma }_n\text{is large}\\ 0\text{if}{\sigma }_n\text{is small}\end{array}\text{, 1}\le n\le N$$

(9)

Hence, these factors tend to discard small singular values of the system matrix $\widetilde{\tilde{\mathbf{\Psi }}}$ and retain large ones.

Many regularization techniques exist in the literature such as the truncated SVD, Tikhonov, etc.; however, due to space limitation we refer the readers to [20] for more information on these techniques. In the next section, we show after a brief description of the LPIC detector that it can be used as a regularization scheme with two regularization parameters.

The LPICdetector

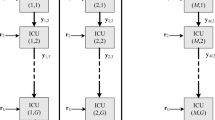
The LPIC detector is an effective scheme for the approximation of the decorrelator/LMMSE detector and it consists of IC units arranged in a multistage structure as shown in Figure 3. The internal structure of each IC unit is illustrated in Figure 4. The vector of decision variables of the p^th stage, n^th branch y_p,n is first multiplied with ${\widetilde{\tilde{\mathbf{\Psi }}}}_n$,added to the vectors of decision variables of the other branches, and then subtracted from the received signal r to obtain a cleaned version of the received signal $\left(\mathbf{r}-{\sum }_{j=1}^N{\widetilde{\tilde{\mathbf{\Psi }}}}_j{y}_{p,j}\right)$where all users exhibit less mutual interference. The vector of decision variables of the (p + 1)^th stage, n^th branch y_{p+ 1,n} is obtained by matched filtering the cleaned signal with ${\widetilde{\tilde{\mathbf{\Psi }}}}_n$, multiplying the result by a weighting factor ω and finally adding the result to the vector of decision variables of the previous stage, that is

$$y_{p+1,n}=y_{p,n}+\omega {\widetilde{\tilde{\mathbf{\Psi }}}}_n^H\left(\mathbf{r}-{\sum }_{j=1}^N{\widetilde{\tilde{\mathbf{\Psi }}}}_j{y}_{p,j}\right)$$

(10)

Figure 3

Multi-stage structure of the LPIC detector.

Figure 4

The p ^th stage IC unit of the LPIC detector.

The weighting factor ω is used to ensure convergence of the LPIC detector. This process is repeated in a multistage structure as shown in Figure 3.

If all N branches of the LPIC detector are considered, then Equation (10) becomes

$${\mathbf{y}}_{p+1}={\mathbf{y}}_p+\omega {\mathbf{e}}_p$$

(11)

where ${\mathbf{e}}_p={\widetilde{\tilde{\mathbf{\Psi }}}}^H\left(\mathbf{r}-\widetilde{\tilde{\mathbf{\Psi }}}{\mathbf{y}}_p\right)$ is the residual error. Therefore, the vector of decision variables and residual error signal can be written in closed form as [21]

$${\mathbf{y}}_{p+1}=\omega \sum _{i=0}^p{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i{\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}={\mathbf{G}}_p^H\mathbf{r}$$

(12)

and

$${\mathbf{e}}_p={\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^p{\mathbf{e}}_0$$

(13)

respectively, where ${\mathbf{e}}_0={\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}$and ${\mathbf{G}}_p=\left[{\mathbf{g}}_{p,1}{\mathbf{g}}_{p,2}\cdots \cdots {\mathbf{g}}_{p,n}\cdots {\mathbf{g}}_{p,N}\right]$. This allows obtaining the average BER at the p^th stage as [21]

$$P_b(p)=\frac{1}{N}{\sum }_{n=1}^N\frac{1}{2^{N-1}}{\sum }_{\underset{b_n=1}{\text{all}\mathbf{b}}}Q\left(\frac{{\mathbf{g}}_{p,n}^H\widetilde{\tilde{\mathbf{\Psi }}}b}{\sigma \sqrt{{\mathbf{g}}_{p,n}^H{\mathbf{g}}_{p,n}}}\right)$$

(14)

where Q(.) denotes the Q- function. Moreover, the LPIC detector converges if

$$\underset{p\to \infty }{lim}{\mathbf{e}}_p\to \mathbf{0}$$

(15)

which translates to the following condition

$$0<\omega <\frac{2}{max{\lambda }_n\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}\text{, 1}\le n\le N$$

(16)

where λ _n is the n^th eigenvalue of the system cross-correlation matrix ${\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}$.

Furthermore, it is easy to show that as the number of stages tends to infinity the LPIC detector converges to the decorrelator detector’s solution, that is

$$\begin{array}{l}\underset{p\to \infty }{lim}{\mathbf{y}}_{p+1}=\underset{p\to \infty }{lim}\omega {\sum }_{i=0}^P{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i{\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}\\ =\omega {\left(\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{-1}{\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}\\ ={\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{-1}{\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}\\ ={\widetilde{\tilde{\mathbf{\Psi }}}}^{†}\mathbf{r}\end{array}$$

(17)

Therefore, if the LPIC detector converges, it converges to the decorrelator detector’s solution that suffers from noise enhancement.

Spectral filtering property of the LPIC detector

In the following, we show that the LPIC detector exhibits a spectral filtering property in the sense that it filters some components of the solution while it retains others. This important property can be exploited to develop a new regularization scheme. To get more insight, we use the SVD of the system matrix $\widetilde{\tilde{\mathbf{\Psi }}}$ to analyze the convergence behavior of the LPIC detector. After some algebraic manipulations, Equation (12) can be written as (see the Appendix for the proof):

$$\begin{array}{l}{\mathbf{y}}_{p+1}=\mathbf{V}\mathbf{F}\left(p+1,\omega \right){\mathbf{\Sigma }}^{-1}{\mathbf{U}}^H\mathbf{r}\\ ={\sum }_{n=1}^N{f}_n\left(p+1,\omega \right)\frac{{\mathbf{u}}_n^H\mathbf{r}}{{\sigma }_n}{\mathbf{v}}_n\end{array}$$

(18)

where F(p + 1,ω) is a K-by-K diagonal matrix with elements f _n (p + 1,ω), known as filtering factors and are given by

$$f_n\left(p+1,\omega \right)=1-{\left(1-\omega {\sigma }_n^2\right)}^{p+1}\text{,}1\le n\le N$$

(19)

These factors tend to attenuate small singular values of the matrix $\widetilde{\tilde{\mathbf{\Psi }}}$ and retain large ones. Moreover, it is clear from Equation (19) that the amount of filtering introduced by the filtering matrix F(p + 1,ω) can be controlled through the stage index p and the weighting factor ω; thus, the stage index and the weighting factor act as regularization parameters for the LPIC detector. Figure 5 depicts the filtering factor f _n (p + 1,ω) as a function of the singular value σ _n for different values of ω and p.

Figure 5

Filter factors of the LPIC detector.

It is clear that as the number of stages p gets larger, more small singular values are included in the reconstruction of the solution y_p+1. However, if small singular values that are below the noise level are involved and the discrete Picard condition is not satisfied, the noise enhancement effect starts dominating the solution. Therefore, the performance of the LPIC detector is expected to improve at early stages but after a certain number of stages the noise starts dominating the solution and deteriorating the performance of the LPIC detector. This explains the phenomenon pointed out in [11–16], which we call here the semi-convergence property of the LPIC detector.

Similar to the stage index p, the weighting factor ω also acts as a regularization factor where the performance of the LPIC detector is expected to improve for small values of ω, but after a certain threshold the noise enhancement effect starts taking place and the performance of the LPIC detector worsens. However, in addition to its regularization effect, the weighting factor ω controls the convergence speed of the LPIC detector, and therefore, the optimal value for this parameter has to balance between high convergence speed and low noise enhancement.

Nevertheless, in practice, the role of the weighting factor is confined to maximize the convergence speed and not to control the amount of noise enhancement introduced into the solution. Consequently, we also restrict the role of the weighting factor to maximize the convergence speed of the LPIC detector and use only the stage index p as a regularization parameter.

Semi-convergence property of the LPIC detector

As mentioned earlier, the LPIC detector exhibits a semi-convergence property where it reaches an average BER that is better than that achieved at final convergence. To get more insight, let us consider the error between y_p+1 and the vector of the transmitted data symbols b, that is

$$\begin{array}{l}\text{b}-{\text{y}}_{p+1}=\text{b}-\text{VF}\left(p+1,\omega \right){\Sigma }^{-1}{\text{U}}^H\text{r}\hfill \\ =\text{b}-\text{VF}\left(p+1,\omega \right){\Sigma }^{-1}{\text{U}}^H\left(\stackrel{\approx }{\mathbf{\Psi }}\text{b+n}\right)\hfill \\ =\text{b}-\text{VF}\left(p+1,\omega \right){\text{V}}^H\text{b}+\text{VF}\left(p+1,\omega \right){\Sigma }^{-1}{\text{U}}^H\text{n}\hfill \\ =\underset{\text{data\hspace{0.5em}error}}{\underbrace{V\left(\text{I}-\text{F}\left(p+1,\omega \right)\right)V^{H}b}}\hfill \\ +\underset{\text{noise\hspace{0.5em}error}}{\underbrace{\text{VF}\left(p+1,\omega \right){\Sigma }^{-1}{U}^{H}n}}\end{array}$$

(20)

It can be seen that the error between y_p+1 (which is an estimate of the vector of the transmitted symbols b) and the vector of the transmitted symbols b consists of two components: the data error and the noise error. The data error is caused by using a modified inverse of the system cross-correlation matrix ${\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}$ instead of the true inverse, whereas the noise error is caused by the magnified/filtered noise. Depending on the filtering matrix F(p + 1,ω), two cases can be distinguished:

•  If F(p + 1,ω) ⋍ I, the data error is small but the noise error is large due to the noise enhancement effect. The solution y_p+1 is under-smoothed.

•  If F(p + 1,ω) ⋍ 0, the noise error is small but the data error is large, and as a result the solution is heavily damped. The solution y_p+1 is over-smoothed.

So, a proper choice of the filtering matrix F(p + 1,ω)should balance between the data and noise errors. And since the amount of filtering introduced by the filtering matrix is proportional to the stage index p and the weighting factor ω, a proper stopping rule needs to be devised. The semi-convergence behavior of the LPIC detector with respect to the stage index p is illustrated in Figure 6 where the norm of the relative error defined by$\frac{{‖\mathbf{b}-{\mathbf{y}}_{p+1}‖}_2}{{‖\mathbf{b}‖}_2}$ is plotted against the stage index p for several values of ω. Since $0<\omega <\frac{2}{max{\lambda }_n\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}$, and $max{\lambda }_n\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)\le tr\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)$, we vary ω as$\omega =\beta \frac{2}{tr\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}$for β = 2, 5, 7, 10, 14.

Figure 6

Norm of the relative error of the LPIC detector vis-à-vis the stage index p.

Similarly, the semi-convergence behavior of the LPIC detector with respect to the weighting factor ω is illustrated in Figure 7 where the norm of the relative error is plotted against the weighting factor ω for several values of p, that is p = 10, 20, 50, 100, and 500.

Figure 7

Norm of the relative error of the LPIC detector vis-à-vis the weighting factor ω.

It is clear from Figure 6 that with increasing values of the weighting factor ω, the convergence speed increases as well and the norm of the relative error exhibits a bowl-shaped curve with a sharp curvature towards the minimum. However, with decreasing values of the weighting factor, the convergence speed decreases and more importantly the bowl-shaped curve exhibits a flat minimum. Similar conclusion can be derived for Figure 7 for the stage index p.

As it will be shown in the simulation results, the average BER of the LPIC detector exhibits the same semi-convergence behavior as for the norm of the relative error in Figures 6 and 7.

Stopping rule for the LPIC detector

In this section, we investigate the possible use of the Morozov discrepancy rule [17, 22] to develop a proper criterion for stopping the iterations of the LPIC detector before the noise enhancement effect starts dominating the solution.

Morozov discrepancy rule for the LPIC detector

The accuracy of the regularized solution y _p cannot exceed that of the received data vector r .

Therefore, if we have an LPIC detector in which the only regularization parameter is the stage index p (the weighting factor is set to one), the best regularized solution y _p is obtained by iterating till the residual error is equal to the noise level, that is

$${‖{\widetilde{\tilde{\mathbf{\Psi }}}}^H\left(\mathbf{r}-\widetilde{\tilde{\mathbf{\Psi }}}{\mathbf{y}}_p\right)‖}_2=\rho$$

(21)

However, due to the fact that the regularization parameter (stage index p) is an integer, the discrepancy principle defined by Equation (21) may not be satisfied exactly; therefore, we reformulate the definition to

$$p_{\mathit{o}\mathit{p}\mathit{t}}=\underset{1\le p\le P}{argmin}\left\{p\right\}\text{s.t.}{‖{\widetilde{\tilde{\mathbf{\Psi }}}}^H\left(\mathbf{r}-\widetilde{\tilde{\mathbf{\Psi }}}{\mathbf{y}}_p\right)‖}_2\le \rho$$

(22)

This condition is illustrated in Figure 8 where at each stage the norm of the residual error ‖e _p ‖₂ of the LPIC detector is evaluated and compared to the noise level ρ. If the residual error becomes less than the noise level then the LPIC detector’s iterations should be stopped. The difference between the norm of the residual error and the noise level is termed the discrepancy error δ and it quantifies the amount of discrepancy resulting from using the modified Morozov discrepancy rule of Equation (22) instead of the exact one described by Equation (21).

Figure 8

Illustration of the Morozov discrepancy rule.

But since we do not have only one regularization parameter (i.e., the stage index p) but we have two instead, that is, p and ω, direct application of Equation (22) is not possible. Therefore, the Morozov discrepancy rule of Equation (22) is modified using the following theorem.

Theorem:

The optimal stage index for the linear PIC detector with regularization parameters p and ω using the Morozov discrepancy rule can be approximated as

$$\begin{array}{l}p{\prime }_{\mathit{o}\mathit{p}\mathit{t}}\simeq \frac{\underset{1\le p\le P}{argmin}\left\{p\right\}\text{s.t.}{‖{\widetilde{\tilde{\mathbf{\Psi }}}}^H\left(\mathbf{r}-\widetilde{\tilde{\mathbf{\Psi }}}{\mathbf{y}}_p\right)‖}_2\le \rho }{\omega }\\ \simeq \frac{p_{\mathit{o}\mathit{p}\mathit{t}}}{\omega },\text{if}\omega \ll \frac{1}{{\sigma }_n^2}\text{,}1\le n\le N\end{array}$$

(23)

Proof:

Two regularization schemes are equivalent if they have the same filter factors. Therefore, an LPIC scheme with only one regularization parameter p is equivalent to another LPIC scheme with two regularization parameters p′ and ω if their filter factors are equal, that is$f_n\left(p\prime ,\omega \right)=f_n\left(p\right)\text{,}1\le n\le N$. As shown in[20, 23], the following approximation can be made

$$\{\begin{array}{l}{f}_n\left(p,\omega \right)\simeq p\omega {\sigma }_n^2\text{if}{\sigma }_n\text{is small}\left(\text{more specifically:}{\sigma }_n^2\ll \frac{1}{\omega }\right)\\ f_n\left(p,\omega \right)\simeq 1\text{if}{\sigma }_n\text{is large}\end{array}$$

Thus, $p\prime \omega {\sigma }_n^2=p{\sigma }_n^2$ and consequently $p=p\prime \omega$ . Hence, Equation ( 23 ) is obtained.

Lemma

$$p{\prime }_{\mathit{o}\mathit{p}\mathit{t}}\simeq \frac{p_{\mathit{o}\mathit{p}\mathit{t}}}{\omega },\text{if}\omega \ll \frac{1}{tr\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}$$

(24)

Proof:

Since${\sigma }_n^2$is upper bounded by$max\left({\sigma }_n^2\right)$and$tr\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)$, that is${\sigma }_n^2\le max\left({\sigma }_n^2\right)\le tr\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)$, hence Equation ( 24 ) is obtained.

Moreover, the discrepancy error δ due to not satisfying the Morozov discrepancy rule is given by

$$\delta =\rho -{‖{\mathbf{e}}_{p_{\mathit{o}\mathit{p}\mathit{t}}}‖}_2$$

(25)

As shown in Figure 8, the discrepancy error δ is a function of two parameters: the initial residual error e ₀ and the weighting factor ω. Obviously, in order to minimize the discrepancy error δ, one should better estimate the noise level ρ using the residual error e _p , that is, making ${‖{\mathbf{e}}_{p_{\mathit{o}\mathit{p}\mathit{t}}}‖}_2$ as close as possible to ρ. This can be realized by reducing the difference between the successive residual errors ${‖{\mathbf{e}}_p‖}_2-{‖{\mathbf{e}}_{p+1}‖}_2$ through employing smaller values of the weighting factor ω[15]. But, unfortunately this will lead to slower convergence of the LPIC detector. Therefore, the weighting factor should be adjusted to realize two conflicting goals: fast convergence and low discrepancy error. A possible solution is to use a stage-dependent weighting factor that exhibits large values in the initial stages where the main goal is improving the convergence speed and small values at later stages where the main goal is reducing the discrepancy error. This subject is outside the scope of this study and it is a research topic by itself and therefore will be treated independently in future study.

Simulation results

This section presents results illustrating the semi-convergence behavior of the linear PIC detector and showing the performance of the LPIC detector equipped with the Morozov discrepancy principle. Figures 9 and 10 depict the average BER of the LPIC detector plotted against the stage index p and the weighting factor ω at SNR = 10 and 20 dB, respectively, with N = 32, K = 4 and the frequency offsets of the four users set to (ɛ₁ = –0.35, ɛ₂ = 0.38, ɛ₃ = 0.36, ɛ₄ = –0.39). The following remarks can be stated.

•  It can be seen that the average BER for both cases (a) and (b) with increasing values of both/either p and/or ω starts initially large, decreases until it reaches the LMMSE detector’s performance and then increases again resulting in an L-shaped valley that illustrates clearly the semi-convergence behavior of the LPIC detector.

•  For varying p, the smaller the value of ω, the more the average BER curve becomes flat around its minimum, and hence the less the sensitivity of the solution to the accuracy of the stopping criterion employed. Note that this reduction in sensitivity is achieved at the expense of slow convergence speed. However, larger values of the weighting factor are needed for faster convergence, but unfortunately this requires a highly reliable stopping criterion to determine the stage index minimizing the average BER. Therefore, the challenge is to develop efficient stopping rules that can be used with high values of the weighting factor so that we can gain both high convergence speed and low average BER.

Figure 9

Semi-convergence behavior of linear LPIC detector with respect to the stage index p and the weighting factor ω for SNR = 10 dB.

Figure 10

Semi-convergence behavior of linear LPIC detector with respect to the stage index p and the weighting factor ω for SNR = 20 dB.

In the following, we evaluate the performance of the LPIC detector equipped with the Morozov discrepancy principle, that we call here Morozov-LPIC detector for brevity. First, we evaluate its convergence behavior by varying the stage index p and assessing its average BER performance for different values of $\omega =\beta \frac{2}{tr\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}$.We set β to 2, 4, 5, 7, 10, SNR = 20 dB, N = 32 and K = 4 with frequency offsets of the four user set to (ɛ₁ = –0.35, ɛ₂ = 0.38, ɛ₃ = 0.36, ɛ₄ = –0.39). Figure 11 shows the results for the four detectors: Morozov-LPIC, LMMSE, Matched Filter (MF), and Decorrelator (DEC).

Figure 11

Convergence behavior of the Morozov-LPIC detector in AWGN channel.

As expected, it is clear that the average BER of the Morozov-LPIC detector gets better and closer to that of the LMMSE detector for smaller values of the weighting factor ω at the expense of slower convergence. Larger values of the weighting factor ω result in faster convergence but unfortunately, with a larger discrepancy error and bad average BER as well.

In Figure 12, the average stopping stage index for each Morozov-LPIC stage is obtained simply by summing up the stopping stage indices determined by the Morozov discrepancy rule for M OFDM symbols and then dividing by M. The average stopping stage index is plotted versus the number of Morozov-LPIC stages. Obviously, as the weighting factor gets smaller (i.e., β = 2) the residual error decreases slower as well and therefore needs more stages to satisfy the Morozov discrepancy rule and hence the average stopping stage index increases with decreasing values of ω as depicted in Figure 12.

Figure 12

Average stopping stage index versus the number of Morozov-LPIC stages in AWGN channel.

Figure 13 illustrates the average BER performance versus the SNR of the Morozov-LPIC and the other three detectors for different values of the weighting factor ω. The maximum number of stages P is fixed to 1000, we set β to 2, 4, 5, 7, 10, N to 32 and K to 4 with frequency offsets as follows (ɛ₁ = –0.35, ɛ₂ = 0.38, ɛ₃ = 0.36, ɛ₄ = –0.39).

Figure 13

Average BER versus SNR performance of the Morozov-LPIC detector in AWGN channel.

As expected, the Morozov-LPIC detector exhibits the best average BER performance for small values of the weighting factor (β = 2). This is clear at high SNRs where the radius of the circle determined by the noise level in Figure 8 gets smaller with increasing SNRs. Hence, for large values of the weighting factor the discrepancy error becomes large as well and consequently the average BER of the Morozov-LPIC detector becomes large too.

In Figure 14, the average stopping stage index for each SNR is obtained simply by summing up the stopping stage indices determined by the Morozov discrepancy rule for M OFDM symbols and then dividing by M. The averaged stopping stage index is plotted versus the SNR.

Figure 14

Average stopping stage index versus SNR of the Morozov-LPIC detector in AWGN channel.

Obviously, the average stopping stage index increases with the SNR because high SNRs translates into smaller noise-level circles as illustrated in Figure 8; therefore, the Morozov-LPIC detector needs more stages to satisfy the Morozov discrepancy rule.

Figure 15 depicts the condition number of the system cross-correlation matrix ${\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}$ for both AWGN channel and Rayleigh fading channels. The different simulation parameters for the AWGN case are set to: N = 32 and K = 4 with frequency offsets set to (ɛ₁ = –0.35,₂ = 0.38, ɛ₃ = 0.36, ɛ₄ = –0.39). For the Rayleigh fading channel case, in addition to the aforementioned simulation parameters, we set the carrier frequency to 3.5 GHz and the speed of different users to, 80, 120, 90, and 100 km/h, respectively. The main difference between the two cases is that the system matrix in a Rayleigh fading channel is time variant and severely ill-conditioned due to the nature of the time-varying fading channel. This imposes some challenges to the performance of the Morozov-LPIC detector where due to the time varying nature of the condition number a fixed weighting factor that might be optimal for one ODFM symbol might result in bad performance for another symbol. In order to overcome this problem, a reasonably small value of the weighting factor should be selected to achieve good performance at the expense of slow convergence rate.

Figure 15

Condition number of the system cross-correlation matrix in case of AWGN and Rayleigh fading channels.

The average BER performance versus the SNR for a Rayleigh fading channel of the Morozov-LPIC detector for different values of the weighting factor ω is plotted in Figure 16. The figure also shows the performance of the DEC, LMMSE, and MF. The maximum number of stages P is fixed to 1000. The remaining parameters are set as follows: β to 2, 4, 6, 12, N to 32, and K to 4 with frequency offsets of the four users are set to (ɛ₁ = –0.35,₂ = 0.38, ɛ₃ = 0.36, ɛ₄ = –0.39). The carrier frequency is set to 3.5 GHz and the speed of different users is set to, 80, 120, 90, and 100 km/h, respectively. Similar to the AWGN channel, using relatively small values of the weighting factor enhances the performance of the Morozov-LPIC detector, however, this results in a very slow convergence rate. For this case, the best performance is achieved for β = 2, and it is expected that for smaller values of β the performance of the Morozov-LPIC detector would improve further.

Figure 16

Average BER versus SNR performance of the Morozov-LPIC detector in Rayleigh fading channel.

In Figure 17, the average stopping stage index is plotted versus the SNR. Similar to Figure 14, the average stopping stage index increases with the SNR and the rate of increase becomes larger for decreasing values of β.

Figure 17

Average stopping stage index versus SNR of the Morozov-LPIC detector in Rayleigh fading channel.

Conclusion

In this study,we unveiled a new property of linear IC detectors. Specifically, we proved that the LPIC detector exhibits a semi-convergence behavior if the discrete Picard condition is not satisfied. Moreover, we showed that this phenomenon can be circumvented if the iterations are stopped before final convergence using a suitable stopping rule. Consequently, we investigated the possible use of the Morozov discrepancy principle to derive a proper stopping condition for the LPIC iterations. Performance analyzes of the LPIC detector using the Morozov discrepancy principle showed that the value of the weighting factor should tradeoff between two conflicting goals: convergence speed and small discrepancy error. Simulation results coincide well with our theoretical findings. Future study includes extending these results to other linear IC detectors such as the SIC, hybrid SIC/PIC, etc., use of stage-dependent weighting factors to compromise between convergence speed and small discrepancy error and finally exploring other stopping rules.

Appendix

Recall that the vector of decision variables is given by

$${\mathbf{y}}_{p+1}=\omega {\sum }_{i=0}^p{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i{\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}={\mathbf{G}}_p^H\mathbf{r}$$

(26)

By expanding the summation in (26) we obtain

$$\begin{array}{l}\sum _{i=0}^p{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i=\mathbf{I}+\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)+\cdots \\ +{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^p\end{array}$$

(27)

Multiplying both terms by $\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)$ and adding the identity matrix I, we obtain:

$$\begin{array}{l}\mathbf{I}+\left(\mathbf{I}-\omega \widetilde{\tilde{\mathbf{\Psi }}}{\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)\sum _{i=0}^p{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i\\ =\mathbf{I}+\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)+\cdots +{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^p\\ +{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{p+1}\\ =\sum _{i=0}^p{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i+{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{p+1}\end{array}$$

(28)

Therefore, the summation in (27) can be expressed as

$$\begin{array}{l}\sum _{i=0}^p{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^i={\omega }^{-1}{\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{-1}\\ x\left(\mathbf{I}-{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{p+1}\right)\end{array}$$

(29)

Hence,

$${\mathbf{y}}_{p+1}={\left({\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{-1}\left(\mathbf{I}-{\left(\mathbf{I}-\omega {\widetilde{\tilde{\mathbf{\Psi }}}}^H\widetilde{\tilde{\mathbf{\Psi }}}\right)}^{p+1}\right){\widetilde{\tilde{\mathbf{\Psi }}}}^H\mathbf{r}$$

(30)

Using the SVD of H defined in (4), Equation (30) can be expressed as

$$\begin{array}{l}{\mathbf{y}}_{p+1}={\left(\mathbf{V}{\mathbf{\Sigma }}^H\mathbf{\Sigma }{\mathbf{V}}^H\right)}^{-1}\left(\mathbf{I}-{\left(\mathbf{I}-\omega \mathbf{V}{\mathbf{\Sigma }}^H\mathbf{\Sigma }{\mathbf{V}}^H\right)}^{p+1}\right)\\ x\mathbf{V}\mathbf{\Sigma }{\mathbf{U}}^H\mathbf{r}\end{array}$$

(31)

which finally can be written as

$$\begin{array}{l}{\mathbf{y}}_{p+1}=\mathbf{V}\left(\mathbf{I}-{\left(\mathbf{I}-\omega {\mathbf{\Sigma }}^H\mathbf{\Sigma }\right)}^{p+1}\right){\mathbf{\Sigma }}^{-1}{\mathbf{U}}^H\mathbf{r}\\ =\mathbf{V}{\mathbf{F}}_{p+1}{\mathbf{\Sigma }}^{-1}{\mathbf{U}}^H\mathbf{r}\end{array}$$

(32)

where ${\mathbf{F}}_{p+1}=\mathbf{I}-{\left(\mathbf{I}-\omega {\mathbf{\Sigma }}^H\mathbf{\Sigma }\right)}^{p+1}$.

This concludes the proof.