Novel two-dimensional DOA estimation with L-shaped array

Abstract

Two-dimensional (2D) direction-of-arrival (DOA) estimation has played an important role in array signal processing. In this article, we address a problem of bind 2D-DOA estimation with L-shaped array. This article links the 2D-DOA estimation problem to the trilinear model. To exploit this link, we derive a trilinear decomposition-based 2D-DOA estimation algorithm in L-shaped array. Without spectral peak searching and pairing, the proposed algorithm employs well. Moreover, our algorithm has much better 2D-DOA estimation performance than the estimation of signal parameters via rotational invariance technique algorithms and propagator method. Simulation results illustrate validity of the algorithm.

1. Introduction

Antenna arrays have been used in many fields, such as radar, sonar, communications, seismic data processing, and so on. The direction-of-arrival (DOA) estimation of signals impinging on an array of sensors is a fundamental problem in array processing, and many DOA estimation methods have been proposed for its solution [1–10]. Uniform linear arrays for estimation of wave arrival have extensively been studied. Compared with uniform linear array, L-shaped array can identify two-dimensional (2D) DOA. 2D-DOA estimation with L-shaped array has been received considerable attention in the field of array signal processing [5–13], and it contains estimation of signal parameters via rotational invariance techniques (ESPRIT) algorithms [5–7], multiple signal classification (MUSIC) algorithm [8], matrix pencil methods [9, 10], propagator methods [11–13], and high-order cumulant method [14].

High-order cumulant method requires the signal statistical properties, and it needs a heavy computation load. MUSIC algorithm is based on the noise subspace, and has a good DOA estimation performance. However, MUSIC requires spectral peak searching, which is computationally expensive. Propagator method has low complexity, but its 2D-DOA estimation performance is less than ESPRIT algorithm. ESPRIT produces signal parameter estimates directly in terms of (generalized) eigenvalues, and the primary computational advantage of ESPRIT is that it eliminates the search procedure inherent. Authors of [5, 6] used ESPRIT method for 2D-DOA estimation with L-shaped array, and Zhang et al. [7] proposed the improved ESPRIT algorithm for 2D-DOA estimation, which had better 2D-DOA estimation performance than that of [5, 6]. The algorithms in [5–7] require an extra paring within 2D-DOA estimation. Paring usually fails to work in the condition of low signal-to-noise ratio (SNR) and the large number of sources.

This study links 2D-DOA estimation problem of L-shaped array to trilinear model, and derives a novel blind 2D-DOA algorithm whose performance is better DOA estimation than ESPRIT algorithms and propagator method. Furthermore, our algorithm employs well without spectral peak searching and pairing. Bro et al. [15] proposed a 2D-DOA algorithm for uniform squares array using trilinear decomposition. There are some differences between this study and that of [15] in some aspects. First, Bro et al. [15] proposed a 2D-DOA algorithm for uniform squares array, while this study is to estimate 2D-DOA for L-shaped array. Second, the received signal of uniform squares array can be modeled directly with trilinear model, and then that of [15] proposed joint azimuth-elevation estimation using trilinear decomposition in uniform squares array. This article is to estimate 2D-DOA estimation in L-shaped array, and the received signal of L-shaped array cannot be modeled directly with trilinear model. We use the cross correlation of received signal for constructing the trilinear model.

The rest of the article is structured as follows. Section 2 develops a data model. Section 3 deals with algorithmic issues. Section 4 presents simulation results, and Section 5 provides conclusions.

2. Data model

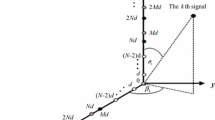
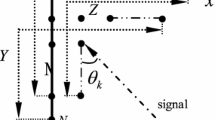
We consider an L-shaped array with 2M - 1 sensors at different locations as shown in Figure 1. A uniform linear array containing M elements is located in y-axis, and the other uniform linear array containing M elements is located in x-axis. We suppose that there are K sources impinge on the L-shaped array with (θ _k ,ϕ _k ), k = 1,2,...,K, where θ _k ,ϕ _k are the elevation and the azimuth angles of the k th source, respectively. The received signal of M elements in x-axis is

Figure 1

The structure of L-shaped array.

$$x\left(t\right)=A_{x}s\left(t\right)+n_x\left(t\right)$$

(1)

where $s\left(t\right)\in {ℂ}^K$ is the source matrix, $n_x\left(t\right)\in {ℂ}^M$ is an M × 1 Gaussian white noise vector of zeros mean and covariance matrix σ²I _M , and $A_x\in {ℂ}^{M\times K}$ is

$$A_x=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill e^{-j{\alpha }_1}\hfill & \hfill e^{-j{\alpha }_2}\hfill & \hfill \cdots \hfill & \hfill e^{-j{\alpha }_K}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{-j\left(M-1\right){\alpha }_1}\hfill & \hfill e^{-j\left(M-1\right){\alpha }_2}\hfill & \hfill \cdots \hfill & \hfill e^{-j\left(M-1\right){\alpha }_K}\hfill \end{array}\right]$$

(2)

where α _k = 2πd cosθ _k sin ϕ _k / λ (k = 1, ..., K), d is the element spacing, and λ is the wavelength. d ≤ λ/2 is required in the array.

The received signal of M elements in y-axis is denoted as

$$y\left(t\right)=A_{y}s\left(t\right)+n_y\left(t\right)$$

(3)

where n _y (t) is an M × 1 Gaussian white noise vector of zeros mean and covariance matrix σ²I _M , and $A_y\in {ℂ}^{M\times K}$ is

$$A_y=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill e^{-j{\beta }_1}\hfill & \hfill e^{-j{\beta }_2}\hfill & \hfill \cdots \hfill & \hfill e^{-j{\beta }_K}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill e^{-j\left(M-1\right){\beta }_1}\hfill & \hfill e^{-j\left(M-1\right){\beta }_2}\hfill & \hfill \cdots \hfill & \hfill e^{-j\left(M-1\right){\beta }_K}\hfill \end{array}\right]$$

(4)

where β _k = 2πd sinθ _k sin ϕ _k / λ, k = 1, ..., K. A _x and A _y are Vandermonde matrices. $x\left(t\right)\in {ℂ}^M$, $y\left(t\right)\in {ℂ}^M$, $A_x\in {ℂ}^{M\times K}$ and $A_y\in {ℂ}^{M\times K}$ are denoted as

$$x\left(t\right)=\left[\begin{array}{c}\hfill x_1\left(t\right)\hfill \\ \hfill x_M\hfill \end{array}\right]=\left[\begin{array}{c}\hfill x_1\hfill \\ \hfill x_2\left(t\right)\hfill \end{array}\right]$$

(5)

$$y\left(t\right)=\left[\begin{array}{c}\hfill y_1\left(t\right)\hfill \\ \hfill y_M\hfill \end{array}\right]=\left[\begin{array}{c}\hfill y_1\hfill \\ \hfill y_2\left(t\right)\hfill \end{array}\right]$$

(6)

$$A_x=\left[\begin{array}{c}\hfill {A_x}_1\hfill \\ \hfill a_{xM}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill a_{x1}\hfill \\ \hfill {A_x}_2\hfill \end{array}\right]$$

(7)

$$A_y=\left[\begin{array}{c}\hfill {A_y}_1\hfill \\ \hfill a_{yM}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill a_{y1}\hfill \\ \hfill {A_y}_2\hfill \end{array}\right]$$

(8)

where x₁ and x _M are first and last rows of x(t), respectively. y₁ and y _M are first and last rows of the y(t), respectively. a_{x 1}and a _xM are first and last rows of the matrix A _x , respectively. a_{y 1}and a _yM are first and last rows of the matrix A _y , respectively.

According to Equations 5-8, we construct the following matrices

$$C_1=E\left\{x_1\left(t\right)y_1{\left(t\right)}^H\right\}={A_x}_1{R}_S{A}_{y_1}^H+N_1$$

(9)

$$C_2=E\left\{x_2\left(t\right)y_1{\left(t\right)}^H\right\}={A_x}_1{\Phi }_x{R}_S{A}_{y_1}^H+N_2$$

(10)

$$C_3=E\left\{x_1\left(t\right)y_2{\left(t\right)}^H\right\}={A_x}_1{R}_S{\Phi }_y^H{A}_{y_1}^H+N_3$$

(11)

$$C_4=E\left\{x_2\left(t\right)y_2{\left(t\right)}^H\right\}={A_x}_1{\Phi }_x{R}_S{\Phi }_y^H{A}_{y_1}^H+N_4$$

(12)

where ${\Phi }_x=\mathsf{\text{diag}}\left(e^{-j{\alpha }_1},e^{-j{\alpha }_2},\dots ,e^{-j{\alpha }_K}\right),$E{.} is the expectation, ${\Phi }_y=\mathsf{\text{diag}}\left(e^{-j{\beta }_1},e^{-j{\beta }_2},\dots ,e^{-j{\beta }_K}\right),$R _S = E{s(t)s(t) ^H } is the source correlation matrix. For independent sources, R _S should be a diagonal matrix with main diagonal vector r = [r₁r₂ ... r _K ]. N₁, N₂, and N₄ are shown as follows.

$$N_1=\left[\begin{array}{cccc}\hfill {\sigma }^2\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right]\in {ℝ}^{K\times K}$$

$$N_2=N_3=N_4=\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right]\in {ℝ}^{K\times K}$$

We define the matrix Ω as

$$\Omega =\left[\begin{array}{c}\hfill r_1\hfill \\ \hfill r_1{e}^{-j{\alpha }_1}\hfill \\ \hfill r_1{e}^{j{\beta }_1}\hfill \\ \hfill r_1{e}^{-j\left({\alpha }_1-{\beta }_1\right)}\hfill \end{array}\right.\begin{array}{c}\hfill r_2\hfill \\ \hfill r_2{e}^{-j{\alpha }_2}\hfill \\ \hfill r_2{e}^{j{\beta }_2}\hfill \\ \hfill r_2{e}^{-j\left({\alpha }_2-{\beta }_2\right)}\hfill \end{array}\begin{array}{c}\hfill \cdots \hfill \\ \hfill \cdots \hfill \\ \hfill \cdots \hfill \\ \hfill \cdots \hfill \end{array}\left.\begin{array}{c}\hfill r_K\hfill \\ \hfill r_K{e}^{-j{\alpha }_K}\hfill \\ \hfill r_K{e}^{j{\beta }_K}\hfill \\ \hfill r_K{e}^{j\left({\alpha }_K-{\beta }_K\right)}\hfill \end{array}\right]$$

(13)

Equations 9-12 can be denoted by

$$C_l={A_x}_1{D}_l\left(\Omega \right)A_{y_1}^H+N_l,l=1,2,...,4$$

(14)

where D _l (.) is to extract the l th row of its matrix and construct a diagonal matrix out of it. Now, the noiseless signal in (14) can be denoted as a trilinear model [16–20], which is shown as

$$x_{m,n,l}={\sum }_{k=1}^K{a}_{m,k}{b}_{n,k}{h}_{l,k},m=1,\dots ,M-1,n=1,\dots ,M-1,l=1,\dots ,4$$

(15)

where a _{m, k} is the (m,k) element of the matrix A_{x 1}, h _{l, k} stands for the (l,k) element of the matrix Ω, b _{n, k} represents the (n,k) element of the matrix $A_{y_1}^{*}$. We hereby consider the signal in (15) as slicing the trilinear model along a direction, within which the symmetry characteristics allow other matrix system rearrangements

$$Y_m=A_{y_1}^{*}{D}_m\left({A_x}_1\right){\Omega }^{\mathsf{\text{T}}},m=\mathsf{\text{1}},\dots ,M-\mathsf{\text{1}}$$

(16)

$$Z_n=\Omega D_n\left(A_{y_1}^{*}\right)A_{x_1}^{\mathsf{\text{T}}}n=\mathsf{\text{1}},\dots ,M-\mathsf{\text{1}}$$

(17)

3. Blind 2D DOA estimation

In this section, we utilize the trilinear decomposition for blind 2D-DOA estimation in L-shaped array, where the received signal has been reconstructed with trilinear model. We use trilinear decomposition for obtaining the direction matrices ${\widehat{A}}_{x1}$ and ${\widehat{A}}_{y1}$, and then DOAs are estimated according to least square (LS) principle.

3.1 Trilinear decomposition

Since trilinear alternating LS (TALS) algorithm is a common data detection method for trilinear model [19], it can be discussed in detail as follows. According to (14), we construct the following matrix in this form

$$C=\left[\begin{array}{c}\hfill C_1\hfill \\ \hfill C_2\hfill \\ \hfill C_3\hfill \\ \hfill C_4\hfill \end{array}\right]=\left[\Omega \odot {A_x}_1\right]A_{y_1}^H+\left[\begin{array}{c}\hfill N_1\hfill \\ \hfill N_2\hfill \\ \hfill N_3\hfill \\ \hfill N_4\hfill \end{array}\right]$$

(18)

where ⊙ stands for Khatri-Rao product. LS fitting is given by

$$\underset{\Omega ,{A_x}_1,{A_y}_1}{min}{∥C-\left[\Omega \odot {A_x}_1\right]A_{y_1}^H∥}_F$$

(19)

LS update for A_{y 1}can be shown as

$${\widehat{A}}_{y_1}^H={\left[\Omega \odot {A_x}_1\right]}^{+}C$$

(20)

Similarly, from the second way of slicing, we have $Y_m=A_{y_1}^{*}{D}_m\left({A_x}_1\right){\Omega }^{\mathsf{\text{T}}},m=\mathsf{\text{1}},\dots ,M-\mathsf{\text{1}}$, which can be rewritten as

$$Y=\left[\begin{array}{c}\hfill Y_1\hfill \\ \hfill Y_2\hfill \\ \hfill ⋮\hfill \\ \hfill Y_{M-1}\hfill \end{array}\right]=\left[{A_x}_1\odot A_{y_1}^{*}\right]{\Omega }^{\mathsf{\text{T}}}$$

(21)

and the LS update for Ω is

$${\widehat{\Omega }}^{\mathsf{\text{T}}}={\left[{A_x}_1\odot A_{y_1}^{*}\right]}^{+}\tilde{Y}$$

(22)

where $\tilde{Y}$ is the noisy signal. Finally, from the third way of slicing, we have $Z_n=\Omega D_n\left(A_{y_1}^{*}\right)A_{x_1}^{\mathsf{\text{T}}},n=\mathsf{\text{1}},\dots ,M-\mathsf{\text{1}}$, which can be rewritten as

$$Z=\left[\begin{array}{c}\hfill Z_1\hfill \\ \hfill Z_2\hfill \\ \hfill ⋮\hfill \\ \hfill Z_{M-1}\hfill \end{array}\right]=\left[A_{y_1}^{*}\odot \Omega \right]A_{x1}^{\mathsf{\text{T}}}$$

(23)

and the LS update for A_{x 1}is

$$A_{x1}^{\mathsf{\text{T}}}={\left[A_{y_1}^{*}\odot \Omega \right]}^{+}\tilde{Z}$$

(24)

where $\tilde{Z}$ is the noisy signal.

According to (20), (22), and (24), the matrices A_{y 1}, Ω, and A_{x 1}are continually updated with conditional LSs, respectively, until convergence. TALS algorithm has several advantages: it is quite easy to implement, guarantee to converge, and comparatively simple to be expanded to the higher-order data. In this article, we use the complex-valued parallel factor analysis model (COMFAC) algorithm [17] for trilinear decomposition. COMFAC algorithm is essentially a fast implementation of TALS, and it can speed up the LS fitting.

For the blind 2D-DOA estimation algorithm that we have investigated, trilinear decomposition has been adopted for obtaining the estimated matrices, and then 2D-DOA estimation is correspondingly shown.

3.2 Identifiablity

In this section, we discuss the sufficient and necessary conditions for uniqueness of trilinear decomposition.

Theorem 1 [19]: Considering $C_l={A_x}_1{D}_l\left(\Omega \right)A_{y_1}^H+N_l$, l = 1,2, ...,4, where ${A_x}_1\in {ℂ}^{\left(M-1\right)\times K}$, ${A_y}_1\in {ℂ}^{\left(M-1\right)\times K}$, and $\Omega \in {ℂ}^{4\times K}$. Concerning that matrix, A_{x 1}and A_{y 1}have been provided with Vandermonde characteristics that the identifiability condition satisfies

$$k_{\Omega }+2\left(M-1\right)\ge 2K+2$$

(25)

where k_Ω is the k th rank [18] of the matrix Ω, the matrices A_{y 1}, Ω, and A_{x 1}are unique up to permutation and scaling of columns.

When the matrix $\Omega \in {ℂ}^{4\times K}$ is full k th rank, Equation 25 becomes

$$min\left(4,K\right)+2\left(M-1\right)\ge 2K+2$$

If K ≥ 4, then min(4,K) = 4 and hence, the identifiability is K ≤ M. If K ≤ 4, then min(4,K) = K and hence, the identifiability in practice becomes K ≤ 2M - 4.

For the received noisy signal, we use trilinear decomposition for obtaining the estimated matrices ${\widehat{A}}_{x1}$, $\widehat{\Omega }$, and ${\widehat{A}}_{y1}$, which are related to A_{y 1}, Ω, and A_{x 1}via

$${\widehat{A}}_{x1}={A_x}_1\Pi {\Delta }_1+V_1$$

(26a)

$${\widehat{A}}_{y1}={A_y}_1\Pi {\Delta }_3+V_3$$

(26b)

$$\widehat{\Omega }=\Omega \Pi {\Delta }_2+V_2$$

(26c)

where ∏ is a permutation matrix, Δ₁, Δ₂, Δ₃ are diagonal scaling matrices satisfying Δ₁, Δ₂, Δ₃ = I _K , V₁, V₂, and V₃ are estimation error matrices. Within trilinear decomposition, permutation and scale ambiguities are inherent. Notably, the scale ambiguity can be resolved by means of normalization.

3.3 DOA estimation for L-shaped array

The direction matrices ${\widehat{A}}_{x1}$ and ${\widehat{A}}_{y1}$ are obtained with trilinear decomposition, and then angles are estimated. a_{x 1}(θ _k , ϕ _k ) is the k th column of A_{x 1}, and it is

$$a_{x1}\left({\theta }_k,{\varphi }_k\right)={\left[1,e^{-j{\alpha }_k},\dots ,e^{-j\left(M-2\right){\alpha }_k}\right]}^{\mathsf{\text{T}}}$$

and then the following vector is obtained by

$$g_x=-\mathsf{\text{angle}}\left(a_{x1}\left({\theta }_k,{\varphi }_k\right)\right)={\left[0,{\alpha }_k,\dots ,\left(M-2\right){\alpha }_k\right]}^{\mathsf{\text{T}}}$$

(27)

where angle(.) is get the phase angles, for each element of complex array. Thereafter, LS principle is adopted for estimating sin ϕ _k cos θ _k . The estimated array steer vector ${\widehat{a}}_{x1}\left({\theta }_k,{\varphi }_k\right)$ (the k th column of the estimated matrix ${\widehat{A}}_{x1}$) is processed through normalization, which also resolves the scale ambiguity, and then normalized sequence is processed for attaining ${\widehat{g}}_x$ according to (27). LSs' fitting is $Pw={\widehat{g}}_x$, where

$$P=\left[\begin{array}{cc}\hfill \begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill ⋮\hfill \\ \hfill 1\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill 0\hfill \\ \hfill 2\pi d∕\lambda \hfill \\ \hfill ⋮\hfill \\ \hfill \left(M-2\right)2\pi d∕\lambda \hfill \end{array}\hfill \end{array}\right],$$

w = [w₀,w _x ]^T, in which w _x is the estimated value of sin ϕ _k cos θ _k , and w₀ is the other estimation parameter. The LS solution to w is

$$\widehat{w}=\left[\begin{array}{c}\hfill {ŵ}_0\hfill \\ \hfill {ŵ}_x\hfill \end{array}\right]={\left(P^{\mathsf{\text{T}}}P\right)}^{-1}{P}^{\mathsf{\text{T}}}{\widehat{g}}_x$$

(28)

Similarly, $a_{y1}\left({\theta }_k,{\varphi }_k\right)={\left[1,e^{-j{\beta }_k},\dots ,e^{-j\left(M-2\right){\beta }_k}\right]}^{\mathsf{\text{T}}}$ is the k th column of A_{y 1}, and then the corresponding vector is g _y = -angle(a_{y 1}(θ _k , ϕ _k )) = [0, β _k ,...,(M-2) β _k ] ^T . We use ${\widehat{A}}_{y1}$ and LS principle to obtain ${}_{ŵ}^y$, which is the estimation of sin ϕ _k sin θ _k . The 2D-DOAs are estimated via

$${\widehat{\varphi }}_k={sin}^{-1}\left(\sqrt{{ŵ}_x^2+{ŵ}_y^2}\right)$$

(29)

$${\widehat{\theta }}_k={tan}^{-1}\left({}_{ŵ}^y∕{ŵ}_x\right)$$

(30)

Up to now, as deducted above, we have proposed the trilinear decomposition-based 2D-DOA estimation for L-shaped array in this section. The algorithmic steps in detail are shown as follows:

Step 1. We collect L snapshots to construct the matrices C _i , i = 1,2,...,4.

Step 2. According to the symmetry characteristics of trilinear model, we obtain Y _m , m = 1,...,M - 1, and Z _n n = 1, ...,M- 1.

Step 3. Initialize randomly for the matrices A_{y 1}, Ω and A_{x 1}.

Step 4. LS update for the source matrix A_{y 1}according to (20).

Step 5. LS update for the source matrix Ω according to (22).

Step 6. LS update for the channel matrix A_{x 1}according to (24).

Step 7. Repeat Steps 4-6 until convergence.

Step 8. Estimate 2D-DOA according to the estimated matrices and LSs principle.

It is noted that our algorithm can obtain automatically paired 2D-DOA estimation. In our algorithm, we employ trilinear decomposition for obtaining the estimated direction matrices ${\widehat{A}}_{x1}={A_x}_1\Pi {\Delta }_1+V_1$, ${\widehat{A}}_{y1}={A_y}_1\Pi {\Delta }_3+V_3$, which suffer from the same column permutation ambiguity, i.e., the i th column of ${\widehat{A}}_{x1}$ corresponds to the i th column of ${\widehat{A}}_{y1}$. So, our algorithm can estimate 2D-DOA estimation without extra pairing.

It is also noted that for the coherent source, spatial smoothing technique is used for attaining full-rank source matrix, followed by our algorithm to estimate coherent DOA. However, the spatial smoothing decreases the array aperture and the identifiable number of targets.

3.4 Complexity analysis and Cramer-Rao lower bounds (CRLB)

In contrast to ESPRIT algorithms in [6, 7], our algorithm has a heavy computational load. For our algorithm, the complexity of each TALS iteration is O(3K³ + 12(M - 1)²K) [16], only a few iterations of this algorithm with COMFAC are usually required to achieve convergence. The total complexity of our algorithm is O{4L(M - 1)² + n(3K³ + 12(M - 1)²K)}, where L is the number of snapshots, and n is the number of iterations. The algorithm in [6] requires O(4L(M - 1)² + 36(M - 1)³ + 2K³), and the ESPRIT algorithm in [7] needs O(4L(M - 1)² + 80(M - 1)³ + 2K³).

We define the matrix A

$$A=\left[\begin{array}{c}\hfill A_x\hfill \\ \hfill {A_y}_2\hfill \end{array}\right]\in {ℂ}^{\left(2M-1\right)\times K}$$

which is also denoted by A = [a₁a₂ ... a _K ], where a _K is the k th column of the matrix A. According to [21], we derive the CRLB for angle estimation in L-shaped array,

$$\mathsf{\text{CRLB}}=\frac{{\sigma }^2}{2L}{\left\{\mathsf{\text{Re}}\left[\left(D^H{\Pi }_A^{\perp }D\right)\oplus P^{\mathsf{\text{T}}}\right]\right\}}^{-1}$$

(31)

where ⊕ stands for Hadamard product.

$${\Pi }_A^{\perp }=I_{2M-1}-A{\left(A^{H}A\right)}^{-1}{A}^H,P=\frac{1}{L}{\sum }_{l=1}^{L}s\left(t_l\right)s^H\left(t_l\right),D=\left[d_1,d_2,\cdots ,d_K,f_1,f_2,\cdots ,f_K\right],d_k=\partial a_k∕\partial {\varphi }_k,f_k=\partial a_k∕\partial {\theta }_k.$$

4. Simulation results

We present Monte Carlo simulations that are to assess 2D-DOA estimation performance of the proposed algorithm. The number of Monte Carlo trials is 1000. There are two signals impinging on L-shaped array with (30°, 30°) and (40°, 40°), respectively. We consider the L-shaped array with 2M - 1 sensors, and a half wavelength of the incoming signals is used for the spacing between the adjacent elements in each uniform linear array. L = 300 snapshots are used in the simulations.

Let $\mathsf{\text{RMSE}}=\frac{1}{K}{\sum }_{k=1}^K\sqrt{\frac{1}{1000}{\sum }_{n=1}^{1000}\left[{\left({\widehat{\varphi }}_{k,n}-{\varphi }_k\right)}^2+{\left({\widehat{\theta }}_k,n-{\theta }_k\right)}^2\right]}$, where ${\widehat{\theta }}_{k,n}$ is the estimate of the elevation angle θ _n of the n th Monte Carlo trial. ${\widehat{\varphi }}_{k,n}$ is the estimation of the azimuth angle ϕ _k of the n th Monte Carlo trial.

We first investigate the convergence performance of our proposed algorithm in this simulation. The sum of squared residuals (SSR) in the trilinear fitting is defined as

$$\text{SSR}={\displaystyle \sum _{m=1}^{M-1}{\displaystyle \sum _{m=1}^{M-1}{\displaystyle \sum _{l=1}^4{[{\tilde{x}}_{m,n,l}-{\displaystyle {\sum }_{k=1}^K{\widehat{a}}_{m,k}{\widehat{b}}_{n,k}{\widehat{h}}_{l,k}}\text{]}}^2}}}$$

where ${\tilde{x}}_{m,n,l}$ is the noisy data. Define DSSR = SSR _i - SSR₀, where SSR _i is the SSR of the i th iteration, SSR₀ is the SSR in the convergence condition. Figure 2 shows the algorithmic convergence performance of COMFAC with 13-antenna-array and SNR = 15 dB. From Figure 2, we find that COMFAC needs few iterations to achieve convergence.

Figure 2

Algorithmic convergence performance.

Figure 3 shows 2D-DOA estimation of the proposed algorithm at SNR = 15 dB, and Figure 4 shows 2D-DOA estimation of our algorithm at SNR = 24 dB. The L-shaped array with 13 antennas is used in Figures 3 and 4. From Figures 3 and 4, we find that our proposed algorithm employs well.

Figure 3

2D-DOA estimation performance at SNR = 15 dB.

Figure 4

2D-DOA estimation performance at SNR = 24 dB.

We compare our algorithm against ESPRIT algorithms [6, 7], propagator method, and CRLB. Their DOA estimation performance comparison is shown in Figure 5, where the L-shaped array with 13 antennas is used. From Figure 5, we find that our algorithm has much better DOA estimation performance than ESPRIT algorithms and propagator method.

Figure 5

Angle estimation performance comparison.

Figure 6 shows 2D-DOA estimation performance of our algorithm with different array configurations. It is seen from Figure 6 that 2D-DOA estimation performance of our algorithm is improved with the number of antennas increasing. When the number of antennas increases, our algorithm has higher received diversity.

Figure 6

Angle estimation performance with different array.

5. Conclusion

This article links the L-shaped array 2D-DOA estimation problem to the trilinear model. To exploit this link, we have proposed trilinear decomposition-based DOA estimation in L-shaped array. Without spectral peak searching and pairing, the proposed algorithm employs well. Furthermore, the proposed algorithm has much better 2D-DOA estimation performance than conventional ESPRIT algorithms and propagator method.

Notations

Bold symbols denote matrices or vectors. Operators (.)*, (.)^T, (.) ^H , (.)^-1, (.)⁺ , and ||.|| _F denote the complex conjugation, transpose, conjugate-transpose, inverse, pseudo-inverse, and Forbenius norm, respectively. I _P denotes a P × P identity matrix. 1_{N× 1}is an N × 1 vector of ones. diag(v) stands for diagonal matrix whose diagonal is the vector v. ⊙ and ⊕ stand for Khatri-Rao and Hadamard product, respectively. E{.} denotes statistical expectation.