Introduction

Recently, to meet the demand on high data rate transmission in communication systems, orthogonal frequency division multiplexing (OFDM) is applied as a modulation scheme. OFDM is a multicarrier modulation technique that operates with specific orthogonality constraints between subcarriers. The orthogonality results a waveform which uses available bandwidth with a high bandwidth efficiency [1]. Also OFDM can be combined with multiple transmit and receive antennas known as multi-input multi-output (MIMO) architecture to improve system capacity and quality of service [2].

However, at the receiver MIMO-OFDM systems require channel state information (CSI) for coherent demodulation and data detection. In order to obtain CSI, blind and training symbol (pilot tones)-based channel estimation techniques are applied. In blind channel estimation technique, CSI is estimated by channel statistics without any knowledge of the transmitted data. But it can suffer from slow convergence in mobile wireless systems because of the time varying nature of channels [3]. In training symbol technique, training sequences that are also called as pilots are inserted into all of subcarriers of OFDM symbols with specific period or inserted into each OFDM symbol [4]. Compared with blind technique, pilot-based channel estimation techniques provide better resistance to fast fading and time varying channels [4–6]. However, designing of pilot tones directly affect the performance of channel estimation algorithms. Hence, optimal design for training symbols based on minimizing Cramer Rao lower bound [7], minimizing mean square error (MSE) of estimation [8–10], and maximizing lower bound capacity [11] has been considered in literature. By minimizing Cramer Rao Bound on MSE of channel, the optimal placement of pilot symbols has been considered in [7]. In [8], the number and the placement of pilot symbols and the power allocation between pilot and information symbols have been optimized in OFDM systems by minimizing error probability. Optimal pilot sequences and optimal uniformly placed pilot tones have been derived with the regard to MSE of LS estimation scheme in MIMO-OFDM systems in [9]. Also in [10], optimal training design for MIMO-OFDM systems with non-uniform placement of pilot tones has been addressed.

Also by utilizing from advantages of the heuristic optimization techniques, the particle swarm optimization (PSO) that is a kind of heuristic optimization technique has been used to solve some problems in communication systems. In [12], blind channel estimation technique based on PSO for power-line communication has been proposed using tracking features of PSO. In [13], continuous and discrete PSO has been used for joint channel and data estimation based on maximum likelihood principle. In [14], to decrease the effect of noise, angle domain PSO-LS algorithm which exploits most significant taps technique using a suitable threshold for MIMO-OFDM systems has been presented. In [15], genetic algorithm (GA) and PSO-based adaptive channel estimation methodology in space time block coded (STBC) OFDM system are investigated to get optimal solution of MMSE algorithm. In this article, LS channel estimation algorithm for MIMO-OFDM systems based on comb-type pilot tones is described briefly. Then optimization of these pilot tones whose design is very crucial for LS channel estimation performance is proposed using PSO. And by optimizing both placement and power of pilot tones, the performance of LS channel estimation algorithm is increased.

This article is organized as follows: the MIMO-OFDM system model and MSE of LS channel estimation method are presented in next section followed by particle swarm optimization, objective function of particle swarm optimization, simulation results and discussion. Finally, this article concludes with the conclusions.

MIMO-OFDM system model

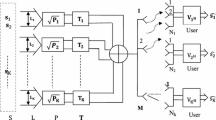
The block diagram of MIMO-OFDM system that has N t transmit antennas, N r receive antennas is presented in Figure 1. At transmitter side, data symbols are mapped by considering modulation type. Pilot symbols are inserted to estimate channels and IFFT is taken at each transmitter antenna. Then cyclic prefix is inserted to prevent inter symbol interference. The transmitted symbol at the p th transmitter antenna includes pilot tones, B p (k), and data symbols. At the q th receiver antenna, after removing cyclic prefix and taking FFT, the received pilot tone vectors expressed as

(1)

where Y q (n) = [Y q (n1),... Y q (n M )]T and B p (n) = [B p (n1),... B p (n M )]T are vectors with the length M. h q,p is L×1 vector from p th transmit antenna to q th receive antenna. L is maximum length of channel. F denotes (1/) times the K×K unitary DFT matrix, W q (n) = [W q (n1),... W q (n M )]T is M×1 additive white Gaussian noise vector, K is number of sub carriers and (.)T is transpose operation. Then h q,p is estimated in channel estimation block and the signal is demodulated [9, 10].

Figure 1
figure 1

Simplified block diagram of MIMO-OFDM system.

Full size image

Least squares (LS) channel estimation

In order to estimate channel state information (CSI), LS is derived as follows:

Assuming training over g consecutive OFDM symbol, the sequence (1) can be written as

(2)

where and

(3)
(4)

channel impulse response h q can be estimated by LS algorithm:

(5)

where At = (AH A)-1AH. It is assumed that pilot sequences are designed such that the gK × LNt sized matrix A is of full column rank LNt which requires gK ≥ LNt. Also M = LNt must be estimated for minimum number of pilot tones.

From Equation 5, MSE of LS channel estimation can be obtained as follows

(6)

If we assume zero mean white noise we have . In this case, the MSE can be written as

(7)

According to (2), minimum MSE of LS channel estimate can be achieved if then minimum MSE can be given by

(8)

where P is a fixed power for the pilot tone, σ2 is noise variance, (.)H is hermitian matrix, (.)t is matrix pseudo inverse, tr(.) is trace, E(.) is expectation [9, 10].

Particle swarm optimization

The particle swarm optimization (PSO) is an evolutionary optimization algorithm whose mechanics are inspired by collaborative behavior of biological populations such as birds flocking and fish schooling to guide particles to search for globally optimal solutions. The advantages of the PSO are its simple implementation and it's quickly convergence ability. In PSO, simple software agent called as particles that represent as potential solutions are placed in the search space of function and evaluate the objective function at their current location. Each particle searches for better position in the search space by changing velocity according to rules that is mentioned as follows

Each particle i has position vector and velocity vector, where D is dimension of solution space. Initially, velocity and position of particles are generated randomly in search space. At each iteration, the velocity and the position of particle i on dimention d are updated as shown below

(9)
(10)

where is the previous best position of particle i, g bestd = (p1, p2,...,pD ) is the best position among all particles, and are uniformly distrubuted numbers in the interval [1, 0], c1 and c2 are cognitive and social parameters and w is inertia weights that are used to maintain momentum of particle [16–19]. The inertia weight w is employed to control the impact of the previous history of velocities on the current velocity, thereby influencing the trade off between global and local exploration abilities of the flying points. A large inertia weight (w) facilitates a global search, while a small inertia weight facilitates a local search. Suitable selection of the inertia weights provides a balance between global and local exploration abilities and thus requires less iteration on the average to find the optimum [17]. In our article, inertia weight w is linearly decreased from wmax to wmin according to

(11)

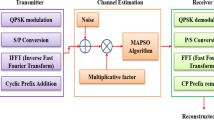
The PSO algorithm steps have been applied as illustrated in Figure 2. As it can be seen from the Figure 2; at first, the particles that represent pilot positions are initialized at random values between 0 and 127 for the system which has 128 subcarriers, and 0 and 63 for the system which has 64 subcarriers. All the possible combinations of particle positions are tested using fitness function that is (discussed in the "Particle swarm optimization objective function" section). If the fitness of particle's current position is better than its previous best position, the velocity and position of particle are updated using Equations 9 and 10. These processes are repeated till the stopping criteria are carried out that are 3000 iterations and 1000 iterations for the systems which have 128 subcarriers and 64 subcarriers, respectively. After the fixed number of iterations, best global particles are chosen as pilot tones positions. Besides, the powers of pilot tones are optimized as mentioned above. However for this purpose, the particles called as power of pilot tones are initialized at random values between 0 and 1.

Figure 2
figure 2

PSO algorithm flow diagram.

Full size image

Particle swarm optimization objective function

In order to optimize pilot tones, MSE function [seen in Equation 8] can be used as objective function for PSO algorithm. However, if this equation is used as the objective function directly, computational complexity will increase because of matrix inversion of Equation 8. In order to reduce computational complexity of Equation 8, Gerschgorin Circle theorem [20] can be used since A is full rank and Eigen values of AAH is positive and real. According to the theorem, upper bound of MSE which will be used as objective function of PSO can be found as

(12)

where λ i (I = 1,...,L) is Eigen values, P b ii = (i = 1,...L) is diagonal elements of matrix (AAH)and Rmax = max(R i ) is the maximum radius of the Gerschgorin disc defined as

(13)

According to the analysis in Equation 12, we can use as objective function for PSO.

Simulation results

The simulation parameters for the MIMO-OFDM system with two transmit antennas and two receive antennas are given in Tables 1 and 2. L = 8 tap channel whose taps are independent, identically distributed and correlated in time with a correlation function according to Jakes model [21, 22] is chosen by assuming there are fd = 5 and fd = 10 Hz. Doppler frequency shifts. In simulations, we evaluate the performance of various pilot tones:

Table 1 MIMO-OFDM simulation parameters for 128 subcarrier
Full size table
Table 2 MIMO-OFDM simulation parameters for 64 subcarrier
Full size table
  1. (a)

    Equipowered random placed pilot tones

  2. (b)

    Equipowered and equispaced orthogonal pilot tones that are in Figure 3

Figure 3
figure 3

The placement of orthogonal pilot tones for (a) 128 subcarrier and 2 transmit antennas and (b) 64 subcarrier and 2 transmit antennas.

Full size image
  1. (c)

    Equipowered and optimized location of pilot tones using PSO that is in Figure 4

Figure 4
figure 4

The placement of optimized pilot tones for (a) 128 subcarrier and 2 transmit antennas and (b) 64 subcarrier and 2 transmit antennas.

Full size image
  1. (d)

    Optimized both power and location of pilot tones using PSO.

The parameters of particle swarm optimization that has been used for the optimization of location and (or) power of pilot tones are given as follows: swarm size = 20 for 128 subcarriers and swarm size = 10 for 64 subcarriers, maximum velocity = 20, inertia factor = 0.9 (start), 0.4 (end), learning factor c1 and c2 = 2.

In Figures 5 and 6, mean square error (MSE) versus SNR(dB) and bit error rate (BER) versus SNR(dB) of different pilot tones for 128 subcarriers over channels with Doppler frequency shift fd = 5 Hz are shown, respectively. From Figure 5, it can be seen that in case of placing pilot tones randomly, the system has poor performance comparing to other methods because of channel estimation errors. The difference of MSE between random pilots and orthogonal pilots is approximately 10-1 at 30 dB SNR. By locating pilot tones uniformly as such in orthogonal pilot tones, instead of placing them randomly, the estimator performance will be increased. As it is seen from Figure 6, orthogonal pilots require 5 dB less SNR than random pilots at BER value of 10-3. However, when pilot tones placement is optimized using PSO unlike orthogonal pilots; we can achieve a 10-1 BER gain at increasing SNR values. Also at 30 dB SNR, BER difference between location optimized pilot tones and random pilot tones is more than 10-1. Besides not only optimizing placement of pilot tones but also optimizing power of them, the estimation performance will be increased much.

Figure 5
figure 5

MSE versus SNR for various pilot tones with 128 subcarriers ( f d = 5 Hz).

Full size image
Figure 6
figure 6

BER versus SNR for various pilot tones with 128 subcarriers ( f d = 5 Hz).

Full size image

The MSE versus SNR(dB) and BER versus SNR(dB) of pilot tones by assuming Doppler shift is fd = 40 Hz are shown in Figures 7 and 8, respectively. According to these figures, when Doppler shifts increase channel estimation errors also increase. However, optimizing pilot tones makes the system robust. Also to show the effect of number of subcarrier on system performance, BER and MSE of the systems which have 64 subcarriers are simulated in Figures 9, 10, 11, and 12. According to these figures, system performance is decreased with the reduction of the subcarrier number. Because a greater number of subcarriers can offer a better protection against multipath delay spread. For instance, when we consider to Figures 6 and 10, at 25 dB SNR value the BER difference of optimized pilot tones is approximately 10-1.

Figure 7
figure 7

MSE versus SNR for various pilot tones with 128 subcarriers ( f d = 40 Hz).

Full size image
Figure 8
figure 8

BER versus SNR for various pilot tones with 128 subcarriers ( f d = 40 Hz).

Full size image
Figure 9
figure 9

MSE versus SNR for various pilot tones with 64 sub carriers ( f d = 5 Hz).

Full size image
Figure 10
figure 10

BER versus SNR for various pilot tones with 64 subcarriers ( f d = 5 Hz).

Full size image
Figure 11
figure 11

MSE versus SNR for various pilot tones with 64 subcarriers ( f d = 40 Hz).

Full size image
Figure 12
figure 12

BER versus SNR for various pilot tones with 64 sub carriers ( f d = 40 Hz).

Full size image

In addition to the performance advantages of PSO which can be seen from above figures, PSO also avoids exhaustive searches to optimize pilot tones location. For each antenna, exhaustive search of pilot position as in orthogonal pilots needs searches for 128 subcarriers and 16 pilot tones; and searches for 64 subcarrier and 8 pilot tones; conversely the number of search in PSO is just 3000 × 20 = 6 × 104 for 3000 iteration and 20 particle sizes.

Here, we investigate the rough computational complexity of orthogonal and optimal placement of pilot tones in terms of Nt (number of transmitter antenna), Nr (number of receiver antennas), Niteration (number of iteration in PSO), n (swarm size), and M (number of pilot tones). Placing of the pilot tones orthogonally as presented in [9] requires NtNrM4 multiplications; also this process has to compute the MSE in Equation 8 for objective function. However, computing this equation is required matrix inversion, as a results M3 additions and multiplications are needed additionally[23]. In contrast, using instead of using MSE in Equation 8 as the objective function, we avoid to compute this matrix inversion to optimize the pilot tones based on PSO. The proposed PSO algorithm needs (NtNr)n multiplication for the fitness of the each position in n sized population at first stage. Velocity and position update in PSO requires µ additional multiplications per iteration. After all iterations, PSO needs Niteration (NtNr)n multiplications. As it can be seen from the above complexity analysis, optimizing location of pilot tones based on PSO has computational complexity advantage over orthogonal placement of pilot tones. The complexity of orthogonal placement of pilot tones becomes quite high when the number of subcarrier is increased. Because increasing number of subcarrier also increase the number of pilot tones in MIMO-OFDM systems.

Conclusion

In this article, we have proposed particle swarm optimization (PSO) to optimize both placement and power of pilot tones which are used in LS channel estimation algorithm based on comb-type pilot tones in MIMO-OFDM systems. From the simulation results, we can see that optimized pilot tones derived by particle swarm optimization outperforms the orthogonal and random pilot tones significantly in terms of MSE and BER. In order to show the effect of Doppler shifts on various pilot tones performance, simulations are carried out over channels with different Doppler shifts values. Furthermore, in objective function of PSO there is no need of computing matrix inversion which is needed to compute MSE values. For this reason this approach has less computational complexity.