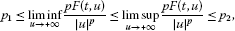Existence of periodic solutions for a class of p-Laplacian equations

Abstract

This paper is devoted to the existence of periodic solutions for the one-dimensional p-Laplacian equation

$$-{\left({\varphi }_p\left(u^{\prime }\right)\right)}^{\prime }=f(t,u),$$

where ${\varphi }_p(u)={|u|}^{p-2}u$ ($1<p<+\mathrm{\infty }$), $f\in C([0,2\pi ]\times \mathbb{R},\mathbb{R})$. By using some asymptotic interaction of the ratios $\frac{f(t,u)}{{|u|}^{p-2}u}$ and $\frac{p{\int }_0^{u}f(t,s)ds}{{|u|}^p}$ with the Fučík spectrum of $-{({\varphi }_p(u^{\prime }))}^{\prime }$ related to periodic boundary condition, we establish a new existence theorem of periodic solutions for the one-dimensional p-Laplacian equation.

1 Introduction and main results

In this paper, we are concerned with the existence of solutions for the following periodic boundary value problem:

$$\{\begin{array}{c}-{({\varphi }_p(u^{\prime }))}^{\prime }=f(t,u),\hfill \\ u(0)=u(2\pi ),u^{\prime }(0)=u^{\prime }(2\pi ),\hfill \end{array}$$

(1.1)

where ${\varphi }_p(u)={|u|}^{p-2}u$ ($1<p<+\mathrm{\infty }$), $f\in C([0,2\pi ]\times \mathbb{R},\mathbb{R})$. A solution u of problem (1.1) means that u is $C^1$ and ${\varphi }_p(u^{\prime })$ is absolutely continuous such that (1.1) is satisfied for a.e. $t\in [0,2\pi ]$.

Existence and multiplicity of solutions of the periodic problems driven by the p-Laplacian have been obtained in the literature by many people (see [1–5]). Many solvability conditions for problem (1.1) were established by using the asymptotic interaction at infinity of the ratio $\frac{f(x,u)}{{|u|}^{p-2}u}$ with the Fučík spectrum for ${({\varphi }_p(u^{\prime }))}^{\prime }$ under periodic boundary condition (see e.g., [2, 4, 6–9]). In [6], Del Pino, Manásevich and Murúa firstly defined the Fučík spectrum for ${({\varphi }_p(u^{\prime }))}^{\prime }$ under periodic boundary value condition as the set ${\mathrm{\Sigma }}_p$ consisting of all the pairs $({\lambda }_{+},{\lambda }_{-})\in {\mathbb{R}}^2$ such that the equation

$$-{\left({\varphi }_p\left(u^{\prime }\right)\right)}^{\prime }={\lambda }_{+}{\left(u^{+}\right)}^{p-1}-{\lambda }_{-}{\left(u^{-}\right)}^{p-1}$$

admits at least one nontrivial 2π-periodic solution (see [10] for $p=2$). Let

$${\pi }_p=2{(p-1)}^{\frac{1}{p}}{\int }_0^1{(1-t^p)}^{-\frac{1}{p}}dt=2{(p-1)}^{\frac{1}{p}}\frac{\pi }{psin(\frac{\pi }{p})}.$$

By [6], it follows that

$${\mathrm{\Sigma }}_p=\{({\lambda }_{+},{\lambda }_{-})\in {\mathbb{R}}^2:{\pi }_p(\frac{1}{\sqrt[p]{{\lambda }_{+}}}+\frac{1}{\sqrt[p]{{\lambda }_{-}}})=\frac{2\pi }{k},k\in {\mathbb{Z}}^{+}\}.$$

Then they applied the Sturm’s comparison theorem and Leray-Schauder degree theory to prove that problem (1.1) is solvable if the following relations hold:

uniformly for a.e. $t\in [0,2\pi ]$ with $p_1,q_1,p_2,q_2>0$ satisfying

$$\frac{2\pi }{(k+1){\pi }_p}<\frac{1}{\sqrt[p]{p_2}}+\frac{1}{\sqrt[p]{q_2}}\le \frac{1}{\sqrt[p]{p_1}}+\frac{1}{\sqrt[p]{q_1}}<\frac{2\pi }{k{\pi }_p},k\in {\mathbb{Z}}^{+}.$$

Clearly, in this case, we have $([p_1,q_1]\times [p_2,q_2])\cap {\mathrm{\Sigma }}_p=\mathrm{\varnothing }$, which is usually called that the nonlinearity f is nonresonant with respect to the Fučík spectrum ${\mathrm{\Sigma }}_p$. In [11], Anane and Dakkak obtained a similar result by using the property of nodal set for eigenfunctions. If f is resonant with respect to ${\mathrm{\Sigma }}_p$, i.e., there exists $({\lambda }_{+},{\lambda }_{-})\in {\mathrm{\Sigma }}_p$ such that ${lim}_{u\to +\mathrm{\infty }}\frac{f(t,u)}{{|u|}^{p-2}u}={\lambda }_{+}$, ${lim}_{u\to -\mathrm{\infty }}\frac{f(t,u)}{{|u|}^{p-2}u}={\lambda }_{-}$ uniformly for a.e. $t\in [0,2\pi ]$, together with the Landesman-Lazer type condition, Jiang [9] obtained the existence of solutions of (1.1) by applying the variational methods and symplectic transformations. In these works, either f is resonant or nonresonant with respect to ${\mathrm{\Sigma }}_p$, the solvability of problem (1.1) was assured by assuming that the ratio $\frac{f(t,u)}{{|u|}^{p-2}u}$ stays at infinity in the pointwise sense asymptotically between two consecutive curves of ${\mathrm{\Sigma }}_p$. Note that

$$\underset{s\to \pm \mathrm{\infty }}{lim\hspace{0.17em}inf}\frac{f(t,s)}{s}\le \underset{s\to \pm \mathrm{\infty }}{lim\hspace{0.17em}inf}\frac{2F(t,s)}{s^2}\le \underset{s\to \pm \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{2F(t,s)}{s^2}\le \underset{s\to \pm \mathrm{\infty }}{lim\hspace{0.17em}sup}\frac{f(t,s)}{s},$$

we can see that the conditions on the ratio $\frac{2F(t,s)}{s^2}$ are more general than that on the ratio $\frac{f(t,s)}{s}$. Recently, Liu and Li [2] studied the nondissipative p-Laplacian equation

$$-{\left({\varphi }_p\left(u^{\prime }\right)\right)}^{\prime }=c{\left({\varphi }_p\left(u^{\prime }\right)\right)}^{\prime }+g(u)-p(t),$$

(1.2)

where $c>0$ is a constant. Define $G(u)={\int }_0^{u}g(s)ds$. They proved that (1.2) is solvable under the following assumptions:

• (1) There exist $b,d_1,d_2>0$ such that $d_1\le \frac{g(u)}{{|u|}^{p-2}u}\le d_2$ for all $|u|\ge b$;

• (2) ${lim}_{u\to +\mathrm{\infty }}\frac{pG(u)}{{|u|}^p}={\lambda }_{+}$, ${lim}_{u\to -\mathrm{\infty }}\frac{pG(u)}{{|u|}^p}={\lambda }_{-}$ with $({\lambda }_{+},{\lambda }_{-})\notin {\mathrm{\Sigma }}_p$.

Here, the potential function G is nonresonant with respect to ${\mathrm{\Sigma }}_p$ and the ratio $\frac{g(u)}{{|u|}^{p-2}u}$ is not required to stay at infinity in the pointwise sense asymptotically between two consecutive branches of ${\mathrm{\Sigma }}_p$ and it may even cross at infinity multiple Fučík spectrum curves.

In this paper, we want to obtain the solvability of problem (1.1) by using the asymptotic interaction at infinity of both the ratios $\frac{f(x,u)}{{|u|}^{p-2}u}$ and $\frac{pF(t,u)}{{|u|}^p}$ with the Fučík spectrum for ${({\varphi }_p(u^{\prime }))}^{\prime }$ under periodic boundary condition. Here, $F(t,u)={\int }_0^{u}f(t,s)ds$. The goal is to obtain the existence of solutions of (1.1) by requiring neither the ratio $\frac{f(x,u)}{{|u|}^{p-2}u}$ stays at infinity in the pointwise sense asymptotically between two consecutive branches of ${\mathrm{\Sigma }}_p$ nor the limits ${lim}_{u\to \pm \mathrm{\infty }}\frac{pF(t,u)}{{|u|}^p}$ exist. We shall prove that problem (1.1) admits a solution under the assumptions that the nonlinearity f has at most $(p-1)$-linear growth at infinity and the ratio $\frac{f(t,u)}{{|u|}^{p-2}u}$ has a $L^1$ limit as $u\to \pm \mathrm{\infty }$, while the ratio $\frac{pF(t,u)}{{|u|}^p}$ stays at infinity in the pointwise sense asymptotically between two consecutive branches of ${\mathrm{\Sigma }}_p$. Our result will complement the results in the literature on the solvability of problem (1.1) involving the Fučík spectrum.

For related works on resonant problems involving the Fučík spectrum, we also refer the interested readers to see [12–19] and the references therein.

Our main result for problem (1.1) now reads as follows.

Theorem 1.1 Assume that $f\in C([0,2\pi ]\times \mathbb{R})$ and the following conditions hold:

• (i) There exist constants $C_1,M>0$ such that

  $$|f(t,u)|\le C_1(1+{|u|}^{p-1}),\mathit{\text{a.e.}}t\in [0,2\pi ],\mathrm{\forall }|u|\ge M;$$

  (1.3)

• (ii) There exists ${\eta }^{\pm }\in L^{\mathrm{\infty }}(0,2\pi )$ such that

  $${\int }_0^{2\pi }|\frac{f(t,u)}{{|u|}^{p-2}u}-{\eta }^{\pm }(t)|dt\to 0\mathit{\text{as}}u\to \pm \mathrm{\infty };$$

  (1.4)

• (iii) There exist constants $p_1,p_2,q_1,q_2>0$ such that

  

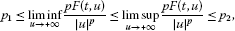  (1.5)

(1.6)

hold uniformly for a.e. $t\in [0,2\pi ]$ with

$$([p_1,p_2]\times [q_1,q_2])\cap {\mathrm{\Sigma }}_p=\mathrm{\varnothing }.$$

(1.7)

Then problem (1.1) admits a solution.

Remark If $f(t,u)=a(t){|u|}^{p-2}{u}^{+}-b(t){|u|}^{p-2}{u}^{-}+e(u)+h(t)$, where $a,b,h\in C[0,2\pi ]$ with $p_1\le a(t)\le p_2$, $q_1\le b(t)\le q_2$ and $p_1,p_2,q_1,q_2>0$ satisfy (1.7), e is continuous on ℝ and ${lim}_{u\to +\mathrm{\infty }}\frac{e(u)}{{|u|}^{p-2}u}=0$, then ${lim}_{u\to +\mathrm{\infty }}\frac{pF(t,u)}{{|u|}^p}=a(t)$ and ${lim}_{u\to -\mathrm{\infty }}\frac{pF(t,u)}{{|u|}^p}=b(t)$. By Theorem 1.1, it follows that problem (1.1) admits a solution. It is easily seen that the result of [16] cannot be applied to this case. Note that one can also obtain the solvability of (1.1) in this case by the result of [6], while in Theorem 1.1 we do not require the pointwise limit at infinity of the ratio $\frac{f(t,u)}{{|u|}^{p-2}u}$ as in [6].

For convenience, we introduce some notations and definitions. $L^p(0,2\pi )$ ($1<p<\mathrm{\infty }$) denotes the usual Sobolev space with inner product ${〈\cdot ,\cdot 〉}_p$ and norm ${\parallel \cdot \parallel }_p$, respectively. $C^m[0,2\pi ]$ ($m\in \mathbb{N}$) denotes the space of m-times continuous differential real functions with norm

$${\parallel x\parallel }_{C^m}=\underset{t\in [0,2\pi ]}{max}|x(t)|+\underset{t\in [0,2\pi ]}{max}|\dot{x}(t)|+\cdots +\underset{t\in [0,2\pi ]}{max}|x^{(m)}(t)|.$$

2 Proof of the main result

Denote by deg the Leray-Schauder degree. To prove Theorem 1.1, we need the following results.

Lemma 2.1 [20]

Let Ω be a bounded open region in a real Banach space X. Assume that $K:\overline{\mathrm{\Omega }}\to \mathbb{R}$ is completely continuous and $p\notin (I-K)(\partial \mathrm{\Omega })$. Then the equation $(I-K)(x)=p$ has a solution in Ω if $deg(I-K,\mathrm{\Omega },p)\ne 0$.

Lemma 2.2 (Borsuk Theorem [20])

Assume that X is a real Banach space. Let Ω be a symmetric bounded open region with $\theta \in \mathrm{\Omega }$. Assume that $K:\overline{\mathrm{\Omega }}\to \mathbb{R}$ is completely continuous and odd with $\theta \notin (I-K)(\partial \mathrm{\Omega })$. Then $deg(I-K,\mathrm{\Omega },\theta )$ is odd.

Proof of Theorem 1.1 Take $({\lambda }_{+},{\lambda }_{-})\in [p_1,p_2]\times [q_1,q_2]$. Consider the following homotopy problem:

$$\{\begin{array}{c}-{({\varphi }_p(u^{\prime }))}^{\prime }=(1-\mu )({\lambda }_{+}{(u^{+})}^{p-1}-{\lambda }_{-}{(u^{-})}^{p-1})+\mu f(t,u)\equiv f_{\mu }(t,u),\hfill \\ u(0)=u(2\pi ),u^{\prime }(0)=u^{\prime }(2\pi ),\hfill \end{array}$$

(2.1)

where $\mu \in [0,1]$.

By (1.3) and the regularity arguments, it follows that $u\in C^1[0,2\pi ]$, and furthermore there exists $a,b\in {\mathbb{R}}^{+}$ such that, if u is a solution of problem (2.1), then

$${\parallel u\parallel }_{C^1}\le a{\parallel u\parallel }_{\mathrm{\infty }}+b.$$

(2.2)

In what follows, we shall prove that there exists $C>0$ independent of $\mu \in [0,1]$ such that ${\parallel u\parallel }_{\mathrm{\infty }}\le C$ for all possible solution $u(t)$ of (2.1). Assume by contradiction that there exist a sequence of number $\{{\mu }_n\}\subset [0,1]$ and corresponding solutions $\{u_n\}$ of (2.1) such that

$${\parallel u_n\parallel }_{\mathrm{\infty }}\to +\mathrm{\infty }\text{as }n\to +\mathrm{\infty }.$$

(2.3)

Set $z_n=\frac{u_n}{{\parallel u_n\parallel }_{\mathrm{\infty }}}$. Obviously, ${\parallel z_n\parallel }_{\mathrm{\infty }}=1$. Define

$${\alpha }_n(t)=\{\begin{array}{cc}\frac{f(t,u_n)}{{|u_n|}^{p-2}{u}_n},\hfill & u_n(t)>M,\hfill \\ 0,\hfill & u_n(t)\le M\hfill \end{array}$$

and

$${\beta }_n(t)=\{\begin{array}{cc}\frac{f(t,u_n)}{{|u_n|}^{p-2}{u}_n},\hfill & u_n(t)<-M,\hfill \\ 0,\hfill & u_n(t)\ge -M.\hfill \end{array}$$

By (1.3), there exists $M_0>0$ such that

$$|{\alpha }_n(t)|,|{\beta }_n(t)|\le M_0,\text{a.e. }t\in [0,2\pi ].$$

Then there exist ${\alpha }_0,{\beta }_0\in L^{\mathrm{\infty }}(0,2\pi )$ such that

$${\alpha }_n(t)\stackrel{\ast }{\rightharpoonup }{\alpha }_0(t),{\beta }_n(t)\stackrel{\ast }{\rightharpoonup }{\beta }_0(t)\text{in }{L}^{\mathrm{\infty }}(0,2\pi ).$$

(2.4)

In addition, using (1.3) and the regularity arguments, there exists $M_1>0$ such that, for each n, we have ${\parallel z_n\parallel }_{C^1}\le M_1$, and thus there exists $z_0\in C^1[0,2\pi ]$ such that, passing to a subsequence if possible,

$$z_n\to z_0\text{in }{C}^1[0,2\pi ].$$

(2.5)

Clearly, ${\parallel z_0\parallel }_{\mathrm{\infty }}=1$. In view of $\{{\mu }_n\}\subset [0,1]$, there exists ${\mu }_0\in [0,1]$ such that, passing to a subsequence if possible,

$${\mu }_n\to {\mu }_0\text{as }n\to +\mathrm{\infty }.$$

(2.6)

Note that for $\mu =0$, problem (2.1) has only the trivial solution, it follows that ${\mu }_0\in (0,1]$. Denote $\overline{\alpha }(t)=(1-{\mu }_0){\lambda }_{+}+{\mu }_0{\alpha }_0(t)$, $\overline{\beta }(t)=(1-{\mu }_0){\lambda }_{-}+{\mu }_0{\beta }_0(t)$. It is easily seen that $z_0$ is a nontrivial solution of the following problem:

$$\{\begin{array}{c}-{({\varphi }_p(z_0^{\prime }))}^{\prime }=\overline{\alpha }(t){(z_0^{+})}^{p-1}-\overline{\beta }(t){(z_0^{-})}^{p-1},\hfill \\ z_0(0)=z_0(2\pi ),z_0^{\prime }(0)=z_0^{\prime }(2\pi ).\hfill \end{array}$$

(2.7)

We now distinguish three cases:

• (i) $z_0$ changes sign in $[0,2\pi ]$;

• (ii) $z_0(t)\ge 0$, $\mathrm{\forall }t\in [0,2\pi ]$;

• (iii) $z_0(t)\le 0$, $\mathrm{\forall }t\in [0,2\pi ]$.

In the following, it will be shown that each case leads to a contradiction.

Case (i). Let

Then, as $n\to +\mathrm{\infty }$, we get

In addition, as shown in [11], we have $|I^0|=0$. Define

$${\eta }_{+}(t)=\{\begin{array}{cc}\eta (t),\hfill & t\in I^{+},\hfill \\ {\alpha }_0(t),\hfill & t\in I^{-},\hfill \end{array}$$

and

$${\eta }_{-}(t)=\{\begin{array}{cc}{\beta }_0(t),\hfill & t\in I^{+},\hfill \\ \eta (t),\hfill & t\in I^{-}.\hfill \end{array}$$

By (1.4) and (2.4), it follows that

$${\alpha }_0(t)\equiv {\eta }_{+}(t),{\beta }_0(t)\equiv {\eta }_{-}(t),\text{a.e. }t\in [0,2\pi ].$$

Thus, $z_0$ satisfies

$$\{\begin{array}{c}-{({\varphi }_p(z_0^{\prime }))}^{\prime }=\tilde{\alpha }(t){(z_0^{+})}^{p-1}-\tilde{\beta }(t){(z_0^{-})}^{p-1},\hfill \\ z_0(0)=z_0(2\pi ),z_0^{\prime }(0)=z_0^{\prime }(2\pi ).\hfill \end{array}$$

(2.8)

Here, $\tilde{\alpha }(t)=(1-{\mu }_0){\lambda }_{+}+{\mu }_0{\eta }_{+}(t)$, $\tilde{\beta }(t)=(1-{\mu }_0){\lambda }_{-}+{\mu }_0{\eta }_{-}(t)$.

Now we prove that there exist $\overline{n}\in {\mathbb{Z}}^{+}$ and $0<{\kappa }_1<1<{\kappa }_2$ such that

$${\kappa }_1\le \frac{max{u}_n}{-min{u}_n}\le {\kappa }_2,\mathrm{\forall }n\ge \overline{n}.$$

(2.9)

In fact, if not, we assume, by contradiction, that there exists a subsequence of $\{u_n\}$, we still denote it as $\{u_n\}$ with $max{u}_n\to \mathrm{\infty }$ and $min{u}_n\to -\mathrm{\infty }$, such that

$$\frac{max{u}_n}{-min{u}_n}\to 0\text{or}\frac{max{u}_n}{-min{u}_n}\to +\mathrm{\infty }.$$

Combing with (2.5), ${\parallel z_0\parallel }_{\mathrm{\infty }}=1$ and the fact that $z_0$ changes sign, we obtain

$$max\frac{u_n}{{\parallel u_n\parallel }_{\mathrm{\infty }}}/(-min\frac{u_n}{{\parallel u_n\parallel }_{\mathrm{\infty }}})\to \frac{max{z}_0}{-min{z}_0}>0.$$

A contradiction. Hence, (2.9) holds.

For any $(t,\mu )\in [0,2\pi ]\times [0,1]$, define

and

$${\overline{F}}_1(t,s,\mu )={\int }_0^s{\overline{f}}_1(t,\tau ,\mu )d\tau ,{\overline{F}}_2(t,r,\mu )={\int }_0^r{\overline{f}}_2(t,\tau ,\mu )d\tau .$$

Denote $s_n=max{u}_n$, $r_n=min{u}_n$. Then by (2.9) it follows that $s_n\to +\mathrm{\infty }$ and $r_n\to -\mathrm{\infty }$. Taking $t_n$ such that $u_n(t_n)=s_n$, $t_n^0$ is the nearest point satisfying $t_n^0<t_n$ and $u_n(t_n^0)=0$. Since $t_n^0,t_n\in [0,2\pi ]$, there exist ${\overline{t}}^0,\overline{t}\in [0,2\pi ]$ such that

$$t_n^0\to {\overline{t}}^0,t_n\to \overline{t}\text{as }n\to +\mathrm{\infty }.$$

(2.10)

By (2.5), we obtain $z_0({\overline{t}}^0)=0$, $z_0(\overline{t})={max}_{t\in [0,2\pi ]}{z}_0(t)$. Note that ${\parallel u_n\parallel }_{\mathrm{\infty }}\to +\mathrm{\infty }$, we have $u_n(t)\to +\mathrm{\infty }$, $\mathrm{\forall }t\in ({\overline{t}}^0,\overline{t})$. Hence, together with ${\mu }_n\to {\mu }_0$ and (1.4), there exist subsequences of $\{u_n\}$ and $\{{\mu }_n\}$, we still denote them as $\{u_n\}$ and $\{{\mu }_n\}$, such that, for a.e. $t\in [0,2\pi ]$,

$$\frac{{\overline{f}}_1(t,u_n(\tau ),{\mu }_n)}{{(u_n(\tau ))}^{p-1}}\to 0,\text{a.e. }\tau \in ({\overline{t}}^0,\overline{t}).$$

Using (1.3), for a.e. $t\in [0,2\pi ]$, $\{\frac{{\overline{f}}_1(t,u_n(\tau ),{\mu }_n)}{{(u_n(\tau ))}^{p-1}}\}$ is uniformly bounded with respect to $\tau \in ({\overline{t}}^0,\overline{t})$, we obtain by the Lebesgue dominated convergence theorem that

$${\int }_{{\overline{t}}^0}^{\overline{t}}\left|\frac{{\overline{f}}_1(t,u_n(\tau ),{\mu }_n)}{{(u_n(\tau ))}^{p-1}}\right|d\tau \to 0,\text{uniformly for a.e. }t\in [0,2\pi ].$$

Thus,

(2.11)

By (1.4) and (2.2), we get

In view of (2.11), we obtain that

$$\left|\frac{p{\overline{F}}_1(t,s_n,{\mu }_n)}{s_n^p}\right|\to 0$$

(2.12)

holds uniformly for a.e. $t\in [0,2\pi ]$. Similarly,

$$\left|\frac{p{\overline{F}}_2(t,r_n,{\mu }_n)}{{|r_n|}^p}\right|\to 0$$

(2.13)

holds uniformly for a.e. $t\in [0,2\pi ]$.

On the other hand, for $\{s_n\}$, $\{r_n\}$ satisfying (2.12)-(2.13), denoting

we obtain by (1.5)-(1.6) that

$$p_1\le {\xi }_1(t)\le q_1,p_2\le {\xi }_2(t)\le q_2,\text{a.e. }t\in [0,2\pi ].$$

(2.14)

Using ${\mu }_n\to {\mu }_0$, we have

(2.15)

(2.16)

We claim that there exists subinterval $I_1\subset [0,2\pi ]$ with $|I_1|>0$ such that

$${\xi }_1(t)-{\eta }_{+}(t)\ne 0,\mathrm{\forall }t\in I_1,$$

(2.17)

or subinterval $I_2\subset [0,2\pi ]$ with $|I_2|>0$ such that

$${\xi }_2(t)-{\eta }_{-}(t)\ne 0,\mathrm{\forall }t\in I_2.$$

(2.18)

Indeed, if not, we assume that ${\eta }_{+}(t)={\xi }_1(t)$, ${\eta }_{-}(t)={\xi }_2(t)$, a.e. $t\in [0,2\pi ]$. Together with the choosing of ${\lambda }_{+}$, ${\lambda }_{-}$ and (2.14), we get

$$p_1\le \tilde{\alpha }(t)\le q_1,p_2\le \tilde{\beta }(t)\le q_2,\text{a.e. }t\in [0,2\pi ].$$

Then by (1.7), it follows that $z_0\equiv 0$. A contradiction. Combining (2.12)-(2.13) with (2.15)-(2.18), we obtain a contradiction.

Case (ii). In this case, we have

$$s_n\to +\mathrm{\infty }\text{ and }\{r_n\}\text{ is uniformly bounded}.$$

Using similar arguments as in Case (i), by (1.4) and (2.4) it follows that ${\alpha }_0(t)\equiv {\eta }_{+}(t)$, $\mathrm{\forall }t\in [0,2\pi ]$. Taking ${\overline{f}}^{+}={\overline{f}}_1$, ${\overline{F}}^{+}={\overline{F}}_1$, a.e. $t\in [0,2\pi ]$. We can see that there exists subsequence of $\{s_n\}$, which is still denoted by $\{s_n\}$, such that

$$\left|\frac{p{\overline{F}}^{+}(t,s_n,{\mu }_n)}{s_n^p}\right|\to 0$$

(2.19)

holds uniformly for a.e. $t\in [0,2\pi ]$. On the other hand, for $\{s_n\}$ satisfying (2.19), denoting

$${\xi }^{+}(t)=\underset{n\to +\mathrm{\infty }}{lim\hspace{0.17em}inf}\frac{pF(t,s_n)}{{|s_n|}^p},$$

we obtain by (1.5) that

$$p_1\le {\xi }^{+}(t)\le q_1,\text{a.e. }t\in [0,2\pi ].$$

(2.20)

Using ${\mu }_n\to {\mu }_0$, we have

(2.21)

We shall show that there exists subinterval $I_{+}\subset [0,2\pi ]$ with $|I_{+}|$ such that

$${\xi }^{+}(t)-{\eta }_{+}(t)\ne 0,\mathrm{\forall }t\in I_{+}.$$

(2.22)

In fact, if not, we assume that ${\eta }_{+}(t)={\xi }^{+}(t)$, a.e. $t\in [0,2\pi ]$. By the choosing of ${\lambda }_{+}$ and (2.20), we get $p_1\le \tilde{\alpha }(t)\le q_1$, a.e. $t\in [0,2\pi ]$. Thus, $z_0$ is a nontrivial solution of the following problem:

$$\{\begin{array}{c}-{({\varphi }_p(z_0^{\prime }))}^{\prime }=\tilde{\alpha }(t)z_0^{p-1},\hfill \\ z_0(0)=z_0(2\pi ),z_0^{\prime }(0)=z_0^{\prime }(2\pi ).\hfill \end{array}$$

(2.23)

Taking 1 as test function in problem (2.23), we get

$$0={\int }_0^{2\pi }\tilde{\alpha }(t)z_0^{p-1}dt.$$

(2.24)

By $\tilde{\alpha }(t)\ge p_1>0$ for a.e. $t\in [0,2\pi ]$, it follows that $z_0(t)=0$ for a.e. $t\in [0,2\pi ]$, which is contrary to that ${\parallel z_0\parallel }_{\mathrm{\infty }}=1$. Hence, (2.22) holds. Clearly, (2.21)-(2.22) contradict (2.19).

Case (iii). In this case, $r_n\to -\mathrm{\infty }$ and $\{s_n\}$ is uniformly bounded. Similar arguments as in Case (ii) imply a contradiction.

In a word, (2.3) cannot hold, and hence by (2.2) there exists $C>0$ independent of $\mu \in [0,1]$ such that, if u is a solution of problem (2.1), then

$${\parallel u\parallel }_{C^1}\le C.$$

(2.25)

Note that, for each $h\in L^{\mathrm{\infty }}(0,2\pi )$, the problem

$$\{\begin{array}{c}-{({\varphi }_p(u^{\prime }))}^{\prime }+{\varphi }_p(u)=h(t),\hfill \\ u(0)=u(2\pi ),u^{\prime }(0)=u^{\prime }(2\pi )\hfill \end{array}$$

(2.26)

has a unique solution $G_p(h)\in C^1[0,2\pi ]$. Clearly, the operator $G_p$ seen as an operator from $C[0,2\pi ]$ into $C^1[0,2\pi ]$ is completely continuous. Define $\psi :C^1[0,2\pi ]\to C[0,2\pi ]$ by $\psi (u)(t)=f(t,u(t))$. Then solving problem (1.1) is equivalent to finding solutions in $C^1[0,2\pi ]$ of the equation

$$u-G_p(\psi (u))=0.$$

Let $(\alpha ,\beta )\in [p_1,q_1]\times [p_1,q_2]$. Define the operator $T_{\alpha ,\beta }:C^1[0,2\pi ]\to C^1[0,2\pi ]$ by $T_{\alpha ,\beta }(u)=G_p({\varphi }_p(u)+\alpha {(u^{+})}^{p-1}-\beta {(u^{-})}^{p-1})$. Denote $B_R=\{u\in C^1[0,2\pi ]:{\parallel u\parallel }_{C^1}<R,R\in \mathbb{R}\}$. Clearly, $deg(I-T_{\alpha ,\beta },B_R,0)$ is well defined for all $R>0$. Owing to ${\lambda }_{+}\cdot {\lambda }_{-}>0$, there is a continuous curve $\alpha (\tau )$, $\beta (\tau )$, $\tau \in [0,1]$, whose image is in ${\mathbb{R}}^2\setminus {\mathrm{\Sigma }}_p$ and $(\lambda ,\lambda )\in \mathbb{R}\setminus {\mathrm{\Sigma }}_p$ such that $(\alpha (0),\beta (0))=({\lambda }_{+},{\lambda }_{-})$, $(\alpha (1),\beta (1))=(\lambda ,\lambda )$. From the invariance property of Leray-Schauder degree under compact homotopies, it follows that the degree $deg(I-T_{\alpha (\tau ),\beta (\tau )},B_R,0)$ is constant for $\tau \in [0,1]$. Obviously, the operator $T_{\lambda ,\lambda }$ is odd. By the Borsuk’s theorem, it follows that $deg(I-T_{\lambda ,\lambda },B_R,0)\ne 0$ for all $R>0$. Thus,

$$deg(I-T_{{\lambda }_{+},{\lambda }_{-}},B_R,0)\ne 0,\mathrm{\forall }R>0.$$

Consider the following homotopy:

$$H(\mu ,u)=G_p({\varphi }_p(u)+(1-\mu )({\lambda }_{+}{\left(u^{+}\right)}^{p-1}-{\lambda }_{-}{\left(u^{-}\right)}^{p-1})+\mu \psi (u)),$$

for $(\mu ,u)\in [0,1]\times C^1[0,2\pi ]$. By (2.25), we can see that there exists $R_0>0$ such that

$$H(\mu ,u)\ne u,\mathrm{\forall }\mu \in [0,1],\mathrm{\forall }u\in \partial B_{R_0}.$$

From the invariance property of Leray-Schauder degree, it follows that

$$\begin{array}{rcl}deg(I-H(1,\cdot ),B_{R_0},0)& =& deg(I-H(0,\cdot ),B_{R_0},0)\\ =& deg(I-T_{{\lambda }_{+},{\lambda }_{-}},B_{R_0},0)\ne 0.\end{array}$$

Hence, problem (1.1) has a solution. The proof is complete. □