Homogeneous-heterogeneous reactions in micropolar fluid flow from a permeable stretching or shrinking sheet in a porous medium

Abstract

The effects of a homogeneous-heterogeneous reaction on steady micropolar fluid flow from a permeable stretching or shrinking sheet in a porous medium are numerically investigated in this paper. The model developed by Chaudhary and Merkin (Fluid Dyn. Res. 16:311-333, 1995) for a homogeneous-heterogeneous reaction in boundary layer flow with equal diffusivities for reactant and autocatalysis is used and extended in this study. The uniqueness of this problem lies in the fact that the solutions are possible for all values of the stretching parameter $\lambda >0$, while for $\lambda <0$ (shrinking surface), solutions are possible only for a limited range of values. The effects of physical and fluid parameters such as the stretching parameter, micropolar parameter, permeability parameter, Schmidt number, strength of homogeneous and heterogeneous reaction parameter on the skin friction, velocity and concentration are analyzed, and these results are presented through graphs. The solute concentration at the surface is found to decrease with the strength of the homogeneous reaction, and to increase with heterogeneous reactions, the permeability parameter and stretching or shrinking parameters. The velocity at the surface was found to increase with the micropolar parameter.

1 Introduction

Micropolar fluids are fluids with internal structures in which coupling between the spin of each particle and the microscope velocity field is taken into account. They represent fluids consisting of rigid, randomly oriented or spherical particles suspended in a viscous medium, where the deformation of fluid particles is ignored. Micropolar fluid theory was introduced by Eringen [1] in order to describe physical systems, which do not satisfy the Navier-Stokes equations. The equations governing the micropolar fluid involve a spin vector and a microinertia tensor in addition to the velocity vector. The potential importance of micropolar fluids in industrial applications has motivated many researchers to extend the study in numerous ways to include various physical effects. The essence of the theory of micropolar fluid lies in particle suspension (Hudimoto and Tokuoka [2]), liquid crystals (Lockwood et al. [3]); animal blood (Ariman et al. [4]), exotic lubricants (Erigen [5]), etc. An excellent review of the various applications of micropolar fluid mechanics was presented by Ariman et al. [6].

Boundary layer flow over a stretching surface is important as it occurs in several engineering processes, for example, materials manufactured by extrusion. During the manufacturing process, a stretching sheet interacts with the ambient fluid both thermally and mechanically. The study of boundary layer flow caused by a stretching surface was initiated by Crane [7]. Recently, several works on the dynamic of the boundary layer flow over a stretching surface have appeared in literature (Dutta et al. [8], Hayat et al. [9], Ishak [10]). The effect of surface conditions on the micropolar flow driven by a porous stretching sheet was studied by Kelson and Desseaux [11]. Mohammadein and Gorla [12] examined the flow of micropolar fluids bounded by a stretching sheet with prescribed wall heat flux, viscous dissipation and internal heat generation. The effect of suction or injection at a stretching surface was studied by Erickson et al. [13] and Fox et al. [14]. The process of suction is used in many engineering activities such as thermal oil recovery, removal of reactants etc. Elbashbeshy and Bazid [15] studied the flow and heat transfer in a porous medium over a stretching surface. Bhargava et al. [16] investigated the flow of a mixed convection micropolar fluid driven by a porous stretching sheet with uniform section. Later, Bhargava et al. [17] studied the same flow of a micropolar flow over a nonlinear stretching sheet. Abel et al. [18] carried out a numerical study of hydromagnetic micropolar fluid flow due to horizontal/vertical stretching sheet using a shooting method. They highlighted a scientific approach for the choice of the missing initial values on which the convergence of the shooting method highly depends. Recently, Narayana and Sibanda [19] studied the effects of laminar flow of a nanoliquid film over an unsteady stretching sheet. Kameswaran et al. [20] studied hydromagnetic nanofluid flow due to a stretching or shrinking sheet with viscous dissipation and chemical reaction effects. Recently, Kameswaran et al. [21] studied homogeneous-heterogeneous reactions in a nanofluid flow over a permeable stretching sheet.

Many chemically reacting systems involve both homogeneous and heterogeneous reactions, with examples occurring in combustion, catalysis and biochemical systems. The interaction between the homogeneous reactions in the bulk of fluid and heterogeneous reactions occurring on some catalytic surfaces is generally very complex, involving the production and consumption of reactant species at different rates both within the fluid and on the catalytic surfaces. A simple mathematical model for homogeneous-heterogeneous reactions in stagnation-point boundary-layer flow was initiated by Chaudhary and Merkin [22]. They modeled the homogeneous (bulk) reaction by isothermal cubic kinetics and the heterogeneous (surface) reaction was assumed to have first-order kinetics. Later Chaudhary and Merkin [23] extended their previous work to include the effect of loss of the autocatalyst. They studied the numerical solution near the leading edge of a flat plate. A model for isothermal homogeneous-heterogeneous reactions in boundary layer flow of a viscous fluid flow past a flat plate was studied by Merkin [24]. Ziabakhsh et al. [25] studied the problem of flow and diffusion of chemically reactive species over a nonlinearly stretching sheet immersed in a porous medium. Chambre and Acrivos [26] studied an isothermal chemical reaction on a catalytic in a laminar boundary layer flow. They found the actual surface concentration without introducing unnecessary assumptions related to the reaction mechanism. The effects of flow near the two-dimensional stagnation point flow on an infinite permeable wall with a homogeneous-heterogeneous reaction was studied by Khan and Pop [27]. They solved the governing nonlinear equations using the implicit finite difference method. It was observed that the mass transfer parameter considerably affects the flow characteristics. Khan and Pop [28] studied the effects of homogeneous-heterogeneous reactions on the viscoelastic fluid toward a stretching sheet. They observed that the concentration at the surface decreased with an increase in the viscoelastic parameter.

The purpose of the present study is to analyze the influence of the permeability, the homogeneous and heterogeneous reaction on the micropolar fluid towards a stretching/shrinking sheet. We transformed the governing momentum and concentration equations into a system of ordinary differential equations using a similarity variable and then numerically solved the equations for some values of the governing parameters. To the best of authors knowledge, such study has not been reported earlier in the literature.

2 Mathematical formulation

Consider steady, incompressible two-dimensional boundary layer flow of a micropolar fluid through a porous medium. The Cartesian coordinates x and y are taken along the surface and are normal to it, respectively, and u and v are the respective velocity components. The flow is generated due to stretching or shrinking of the sheet caused by the simultaneous application of two equal forces along the x-axis. Keeping the origin fixed, it is assumed that the surface is stretched/shrunk with a linear velocity $u_w(x)=U_{w}x$, where $U_w$ is a constant with $U_w>0$ for a stretching sheet, $U_w<0$ for a shrinking sheet and $U_w=0$ for a static sheet. We consider a simple model for the interaction between a homogeneous (or bulk) reaction and a heterogeneous (or surface) reaction involving the two chemical species A and B in a boundary layer flow proposed by Merkin [24] and Chaudhary and Merkin [22, 23] in the following form:

(2.1)

(2.2)

Here a and b are concentrations of chemical species A and B, and $k_i$ ($i=c,s$) are the rate constants. We also assume that both reaction processes are isothermal. It is also assumed that the ambient fluid moves with a velocity $u_e(x)=U_{\mathrm{\infty }}x$, where $U_{\mathrm{\infty }}$ is a constant, in which there is a uniform concentration $a_0$ of reactant A and in which there is no autocatalyst B over a flat surface.

Under these assumptions, the governing equations lead to

(2.3)

(2.4)

(2.5)

(2.6)

(2.7)

where $K_1$ is the permeability of the porous medium, ϵ is the porosity, μ is the dynamic viscosity, ${\mu }_{\mathrm{eff}}$ is the effective dynamic viscosity, κ is the vortex viscosity, ρ is the fluid density, N is the microrotation, $j=(\nu /U_{\mathrm{\infty }})$ is the microinertia per unit mass and γ is the spin gradient viscosity defined as

$$\gamma =\mu (1+K_p/2)j,$$

(2.8)

where $K_p=\kappa /\mu$ is the material or micropolar parameter. The corresponding boundary conditions are

(2.9)

where $v_w$ is the constant mass flux with $v_w<0$ for suction and $v_w>0$ for injection (blowing), respectively; n is a constant such that $0\le n\le 1$, where the case $n=0$ is called strong concentration (Guram and Smith [29]), indicates $N=0$ near the surface and represents concentrated particle flows in which the microelements close to the surface are unable to rotate (Jena and Mathur [30]). The case $n=1$ is used for the modeling of turbulent boundary layer flow (Peddieson [31]). The case $n=1/2$ indicates the vanishing of the antisymmetrical part of the stress tensor and denotes weak concentration (Ahmadi [32]), which is the case considered in the present study. We introduce the stream function ψ, where $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$, which satisfies the continuity equation identically. Using similarity variables of the form

$$\begin{array}{r}\psi ={(U_{\mathrm{\infty }}\nu )}^{1/2}xf(\eta ),\eta ={(U_{\mathrm{\infty }}/\nu )}^{1/2}y,\\ N={(U_{\mathrm{\infty }}/\nu )}^{1/2}{u}_{\mathrm{\infty }}xp(\eta ),g(\eta )=a/a_0,h(\eta )=b/a_0,\end{array}$$

(2.10)

the governing equations are written as the following system of ordinary differential equations:

(2.11)

(2.12)

(2.13)

(2.14)

where $\chi =\frac{{\mu }_{\mathrm{eff}}ϵ}{U_{\mathrm{\infty }}{K}_1\rho }$ is the permeability parameter, $\mathit{Sc}=(\nu /D_A)$ is the Schmidt number, $K=(k_c{a_0}^2/U_{\mathrm{\infty }})$ gives a measure of the strength of the homogeneous reaction, $\delta =(D_B/D_A)$ is the ratio of the diffusion coefficient and primes denote differentiation with respect to η. The boundary conditions (equation (2.9)) are written as

(2.15)

(2.16)

where $s=-\frac{v_w}{{(U_{\mathrm{\infty }}\nu )}^{1/2}}$ is the mass transfer parameter with $s>0$ for suction, $s<0$ for injection and $s=0$ for an impermeable surface. $\lambda =u_w/u_e$ is the stretching parameter where $\lambda >0$ corresponds to a stretching surface and $\lambda <0$ corresponds to a shrinking surface. $K_s=(k_{s}l{\mathit{Re}}^{-1/2}/D_A)$ measures the strength of the heterogeneous (surface) reaction and $\mathit{Re}=(U_{\mathrm{\infty }}l/\nu )$ is the Reynolds number.

It is expected that the diffusion coefficients of chemical species A and B are of comparable size, which leads us to further assumption that the diffusion coefficients $D_A$ and $D_B$ are equal, i.e., $\delta =1$ (Chaudhary and Merkin [22]). This assumption leads to the following relation:

$$g(\eta )+h(\eta )=1.$$

(2.17)

Thus, equations (2.13) and (2.14) reduce to

$$\frac{1}{\mathit{Sc}}{g}^{″}+f{g}^{\prime }-Kg{(1-g)}^2=0,$$

(2.18)

and the boundary conditions equation (2.16) take the form

$$g^{\prime }(0)=K_{s}g(0),g(\mathrm{\infty })=1.$$

(2.19)

The physical quantity of interest is the skin friction coefficient $C_f$. It characterizes the surface drag. The shearing stress at the surface of the wall ${\tau }_w$ is given by

$${\tau }_w={[(\mu +\kappa )\frac{\partial u}{\partial y}+\kappa N]}_{y=0}.$$

(2.20)

The skin friction coefficient is defined as

$$C_f=\frac{2{\tau }_w}{\rho u_w^2}.$$

(2.21)

Using the similarity variables in the above equation, we obtain

$$C_f\sqrt{{\mathit{Re}}_x}=(1+K/2)f^{″}(0),$$

(2.22)

where ${\mathit{Re}}_x$ represents the local Reynolds number defined by ${\mathit{Re}}_x=x{u}_e(x)/\nu$. In the present paper, we consider only the case $s\ge 0$ (suction) and $n=1/2$ (weak concentration).

3 Results and discussion

The system of ordinary differential equations (2.10), (2.11) and (2.17) along with the boundary conditions (2.15) and (2.19) are solved numerically for some values of λ, $K_p$, $K_s$, k, χ and Sc using Matlab bvp4c routine. We compare our results for a stretching sheet with those reported by Wang [33], Ishak et al. [34] and Rosali et al. [35] in Table 1; and for the shrinking sheet, we compare our results with those reported by Rosali et al. [35] in Table 2. These show an excellent agreement with our present results. This investigation confirms that the existence and uniqueness of solution depends on the stretching/shrinking sheet parameter. It is also found that the solutions of equations (2.10), (2.11) and (2.17) can be obtained for all values of λ, while for the case of a shrinking surface ($\lambda <0$), the governing equations have the solution only in the range of $\lambda >{\lambda }_c$, where ${\lambda }_c$ is a critical value of λ, which depends on the other parameter, and we have no solution for $\lambda <{\lambda }_c$. A dual solution appears for the range ${\lambda }_c\le \lambda <-1$. We have plotted the velocity profile, concentration profile and concentration at the surface for different parameters. In this problem, we have shown single as well as dual solution. As was mentioned by Merkin [36], Merrill et al. [37] and Rosali et al. [35], the first solution is stable and physically realizable, while the second solution is unstable. Although the second solution seems to be deprived of physical significance, it is interesting in nonlinear differential equation theory, since a similar equation may reappear in some other situations where the corresponding solution could have a more realistic meaning.

Table 1 Comparison of ${\mathit{f}}^{\mathbf{″}}\mathbf{(}\mathbf{0}\mathbf{)}$ for a stretching sheet obtained for different values of λ , for fixed values of $\mathit{\chi }\mathbf{=}\mathbf{0}$ , ${\mathit{K}}_{\mathit{p}}\mathbf{=}\mathbf{0}$ and $\mathit{s}\mathbf{=}\mathbf{0}$

Table 2 Comparison of ${\mathit{f}}^{\mathbf{″}}\mathbf{(}\mathbf{0}\mathbf{)}$ for a shrinking sheet obtained for different values of λ , for fixed values of $\mathit{\chi }\mathbf{=}\mathbf{0}$ , ${\mathit{K}}_{\mathit{p}}\mathbf{=}\mathbf{0}$ and $\mathit{s}\mathbf{=}\mathbf{0}$

From Table 1, it is clear that the skin friction is a decreasing function of λ. All values of the skin friction coefficient are positive for $\lambda <1$, while they are negative when $\lambda >1$. Physically, the negative values of the skin friction coefficient correspond to the surface exerting a drag force on the fluid and the opposite sign implies the inverse phenomenon. The skin friction coefficient is zero when $\lambda =1$ regardless of the values of other parameters. This is because for $\lambda =1$, there is no shear stress at the surface as the surface and fluid move with the same velocity.

The effect of the stretching/shrinking parameter λ for $\lambda <0$ is shown in Table 2. It is evident that initially the skin friction is an increasing function of λ, but it decreases after a certain value of λ. As mentioned earlier, the solution of the equations is possible only in the range of $\lambda >{\lambda }_c$. It is evident that the value of ${\lambda }_c$ depends on other parameters $K_p$, s and n. The value of ${\lambda }_c$ is approximate to −1.2465 when $K_p=0$ and $s=0$, while introducing $K_p=0.1$ and $s=0.5$, we get ${\lambda }_c\approx -1.5144$. It is also observed that the first solution is a decreasing function of λ, whereas the second solution is an increasing function of λ. It is interested to note that these both solutions coincide at $\lambda ={\lambda }_c$.

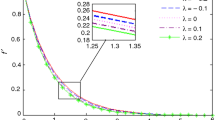
The variation of the velocity and concentration profiles is plotted as a function of η for some values of λ in Figure 1. (i) For $\lambda >0$ (stretching surface), the fluid velocity is becoming increasingly greater than the free stream. In this case the fluid velocity decreases with the value of η and converges at unity as per the condition. (ii) For $\lambda =0$ (static surface), the fluid velocity initially is stationary, but with η value it increases in a nonlinear way. (iii) For $\lambda <0$ (shrinking surface), the fluid velocity is initially negative, but it increases with η, and after a certain value of η, it becomes positive. For the concentration profile, all the curves are started from the origin and they increase nonlinearly with η to follow ‘S’ shape and finally reach unity according to the given condition. For $\lambda =-1.2$ and −1.3, the graphs contain a dual solution. From the boundary condition, it is clear that the velocity at the surface is equal to λ; and so with increase in λ, the momentum boundary layer thickness increases for the case of the first solution, while an opposite phenomenon appears for the second solution which concurs with the results reported by Bhattacharyya et al. [38]. It shows that for the first solution, the concentration boundary layer thickness increases with increase in λ, while it decreases for the second solution.

Figure 1

Effect of λ on (a) and (b) for ${\mathit{K}}_{\mathit{p}}\mathbf{=}\mathbf{0.1}$ , $\mathit{\chi }\mathbf{=}\mathbf{0.1}$ , $\mathit{Sc}\mathbf{=}\mathbf{1}$ , $\mathit{K}\mathbf{=}\mathbf{1}$ , $\mathit{s}\mathbf{=}\mathbf{0.5}$ , $\mathit{n}\mathbf{=}\mathbf{0.5}$ , ${\mathit{K}}_{\mathit{s}}\mathbf{=}\mathbf{1}$ .

The effect of the micropolar parameter and suction parameter on the velocity and concentration profile is shown in Figure 2. A comparison is made for the Newtonian fluid ($K_p=0$) and the micropolar fluid ($K_p>0$). It shows that momentum boundary layer thickness is more for the micropolar fluid rather than for the Newtonian one, i.e., the micropolar parameter increases the velocity of the fluid, which is similar to the results given by Ishak et al. [34]. A similar phenomenon is observed for concentration boundary thickness. The velocity of the fluid is reduced due to suction, and this leads to an increase in the solute concentration.

Figure 2

Variation of ${\mathit{K}}_{\mathit{p}}$ and s on (a) and (b) for $\mathit{\lambda }\mathbf{=}\mathbf{2}$ , $\mathit{\chi }\mathbf{=}\mathbf{0.5}$ , $\mathit{Sc}\mathbf{=}\mathbf{1}$ , $\mathit{K}\mathbf{=}\mathbf{1}$ , $\mathit{n}\mathbf{=}\mathbf{0.5}$ , ${\mathit{K}}_{\mathit{s}}\mathbf{=}\mathbf{1}$ .

The effect of the homogeneous and heterogeneous reaction on the concentration profile is shown in Figure 3. The effect of heterogeneous and homogeneous reactions separately is shown through Figures 3(a) and 3(b), respectively. We considered $\lambda =-1.2$ and so a dual solution appeared. It is evident that the concentration boundary layer of the reactants is increasing with η in both cases, and after a certain η value, they all coincide, i.e., after a certain η value, the homogeneous and heterogeneous reactions have no effect on the concentration of the reactants. This critical value of η (${\eta }_{\mathrm{\infty }}$) depends on the strength of the homogeneous reaction and increases with the value of K, but it does not depend on the strength of the heterogeneous reaction. A similar phenomenon is observed for the second solution. The graphs for the second solution with $K_s=0.2$ and 1 coincide. It is observed that the first solution is more stable and converges more easily than the second solution.

Figure 3

Effect of λ on (a) and (b) for ${\mathit{K}}_{\mathit{p}}\mathbf{=}\mathbf{0.1}$ , $\mathit{\chi }\mathbf{=}\mathbf{0.1}$ , $\mathit{Sc}\mathbf{=}\mathbf{1}$ , $\mathit{s}\mathbf{=}\mathbf{0.5}$ , $\mathit{n}\mathbf{=}\mathbf{0.5}$ .

The concentration of the reactants depends on the Schmidt number (Sc) and heterogeneous reaction parameter. The variation of the concentration with K for different values of the Schmidt number and $K_s$ is shown in Figure 4. The Schmidt number is the ratio between a viscous diffusion rate and a molecular diffusion rate. For a fixed molecular diffusion rate, with increase in Schmidt number, the viscous diffusion rate increases, which reduces the velocity of the nanofluid and helps to increase the concentration of the nanofluid. Homogeneous reaction parameter and heterogeneous reaction parameter influence the reaction rate of the solute and help to reduce the concentration of the reactants, which concurs with the results reported by Khan and Pop [28].

Figure 4

Concentration at the surface effect on (a) and (b) for ${\mathit{K}}_{\mathit{p}}\mathbf{=}\mathbf{1}$ , $\mathit{\chi }\mathbf{=}\mathbf{0.5}$ , $\mathit{s}\mathbf{=}\mathbf{0.8}$ , $\mathit{n}\mathbf{=}\mathbf{0.5}$ .

4 Conclusions

The present analysis investigates the effect of the homogeneous and heterogeneous reaction on the micropolar fluid flow through a porous medium past a porous stretching/shrinking sheet with suction. The momentum and concentration equations were transformed into a set of coupled nonlinear differential equations using similarity transformations and solved numerically by Matlab bvp4c package. We compared our results with those in the literature for some limiting case. A dual solution appeared for the shrinking sheet case. The effect of the dual solution is shown by tables and graphs. The momentum boundary layer thickness increased for the case of the first solution, while an opposite phenomenon appeared for the second solution and a similar phenomenon was observed for concentration profile. It was observed that the concentration at the surface decreased with the strengths of the homogeneous and heterogeneous reactions. The solute concentration, however, increased with the permeability and stretching/shrinking parameters. The velocity of the fluid and the concentration of the reactants at the surface increase with the stretching/shrinking parameter. Also, velocity increases due to the increase in micropolar parameter. The concentration of the reactants decreases with the strength of the homogeneous and heterogeneous reaction.