Abstract
We develop a formulation for the analytic or approximate solution of fractional differential equations (FDEs) by using respectively the analytic or approximate solution of the differential equation, obtained by making fractional order of the original problem integer order. It is shown that this method works for FDEs very well. The results reveal that it is very effective and simple in determination of solutions of FDEs.
Similar content being viewed by others
1 Introduction
Fractional differential equations (FDEs) are obtained by generalizing differential equations to an arbitrary order. Since fractional differential equations are used to model complex phenomena, they play a crucial role in engineering, physics and applied mathematics. Therefore they have been generating increasing interest from engineers and scientist in recent years. Since FDEs have memory, nonlocal relations in space and time, complex phenomena can be modeled by using these equations. Due to this fact, materials with memory and hereditary effects, fluid flow, rheology, diffusive transport, electrical networks, electromagnetic theory and probability, signal processing, and many other physical processes are diverse applications of FDEs [1–7].
In [8], the solutions for some nonlinear fractional differential equations are constructed by using symmetry analysis. But, in general, FDEs do not have exact analytic solutions, hence the approximate and numerical solutions of these equations are studied. Analytical approximations of linear and nonlinear FDEs are obtained by the variational iteration method, Adomian’s decomposition method, the homotopy perturbation method and the Lagrange multiplier method [9–24].
In the present paper, we use the Taylor series of an analytical solution for the differential equations which is obtained from FDEs by making the fractional order of the derivative integer, to obtain the analytical or approximate solution of FDEs. We can obtain the exact or approximate solution of FDEs by changing the terms of Taylor series expansion for a solution of a differential equation in such a way that the relationship among the terms of Taylor series expansion in the sense of derivative and fractional derivative remains the same. Applications of this method show that it is easy and effective when applied to any FDEs as long as the differential equation obtained from FDEs has an analytical or approximate solution. We take the fractional derivative in the Caputo sense.
The structure of this article is as follows. In Section 2, we give the construction of analytical or approximate solutions for FDEs including fractional derivative with respect to time. In the same manner, we obtain the analytical or approximate solution of FDEs with fractional derivative with respect to space variable in Section 3. In Section 4, we take the combination of previous two sections, and we get the analytical or approximate solution of FDEs with fractional derivative with respect to time and space variable. Finally, we give some illustrative examples of this method for all cases in Section 5.
2 Solution of FDEs including fractional derivative with respect to time
Let us consider the following FDE:
In order to determine the solution of this equation, we first need to determine the solution of the following differential equation:
which is obtained by taking . After finding an analytic or approximate solution of equation (2), we can obtain the exact or approximate solution of equation (1) by changing the terms of Taylor series expansion for the solution of differential equation (2) in such a way that the relationship among the terms of Taylor series expansion in the sense of derivative and fractional derivative with respect to time remains the same. In other words, we expand the exact or approximate solution into its Taylor series with respect to t. Then we replace the derivatives with respect to t by fractional derivatives with respect to t in such a way that the relation among the terms of Taylor series is preserved. Moreover, we leave the first m terms of Taylor series fixed since . This also allows the solution of the fractional differential equation to satisfy the initial conditions of the problem. Let us assume that the solution of equation (2) is expanded into its Taylor series with respect to t as follows:
Then the solution of equation (1) becomes
For instance, let us assume that and the solution of equation (2) is . In order to find the solution of equation (1), we expand this solution into Taylor series with respect to t as follows:
Based on (4), the solution of equation (1) can be written in the following form:
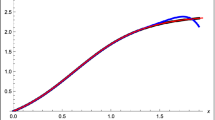
Figures 1-3 show the evolution results for the expansion (5) obtained for different values of α.
3 Solution of FDEs including fractional derivative with respect to space variable
Let us consider the following FDE:
In order to determine the solution of this equation, we first need to determine the solution of the following differential equation:
which is obtained by taking .
After finding the analytic or approximate solution of equation (7), we can obtain the exact or approximate solution of equation (6) by changing the terms of Taylor series expansion for the solution of differential equation (7) in such a way that the relationship among the terms of Taylor series expansion in the sense of derivative and fractional derivative with respect to space remains the same. In other words, we expand the exact or approximate solution into its Taylor series with respect to x. Then we replace the derivatives with respect to x by fractional derivatives with respect to x in such a way that the relation among the terms of Taylor series is preserved. Moreover, we leave the first m terms of Taylor series fixed since . This also allows the solution of the fractional differential equation to satisfy the boundary conditions of the problem.
Let us assume that the solution of equation (7) is expanded into its Taylor series with respect to x as follows:
Then the solution of equation (6) becomes
For instance, let us assume that and the solution of equation (7) is . In order to find the solution of equation (6), we expand this solution into Taylor series with respect to x as follows:
Based on (9), the solution of equation (6) can be written in the following form:
Figures 4-6 show the evolution results for the expansion (10) obtained for different values of α.
4 Solution of FDEs including fractional derivative with respect to space variable and time
Let us consider the following linear FDE with constant coefficients:
In order to determine the solution of this equation, we first need to determine the solution of the following differential equation:
which is obtained by taking , . Since it is a linear partial differential equation, its solution can be written as
After finding the analytic or approximate solution of equation (12), we expand into its Taylor series with respect to x and into its Taylor series with respect to t. Then we replace the derivatives with respect to x by fractional derivatives with respect to x in in such a way that the relation among the terms of Taylor series is preserved. Moreover, we leave the first m terms of Taylor series fixed since . Similarly, we do the same thing for . This also allows the solution of the fractional differential equation to satisfy the initial and boundary conditions of the problem. Let us assume that of equation (12) is expanded into its Taylor series with respect to x as follows:
Then of solution (13) becomes
Let us assume that of equation (12) is expanded into its Taylor series with respect to t as follows:
Then of solution (13) becomes
For instance, let us assume that , , and that the solution of equation (12) is . In order to find the solution of equation (11), we first expand into Taylor series with respect to x as follows:
Similarly,
Based on (4) and (9), the expansions of and can be written in the following form:
and then the solution of equation (11) can be written in the following form:
5 Illustrative applications
Example 1
Let us consider the following time-fractional initial boundary value problem:
The exact solution, for the special case , is given by
Now we can apply series (4) to construct the solution for , and we have
which is exactly the same solution as in [18].
Example 2
Let us consider the following time-fractional initial boundary value problem:
The exact solution, for the special case , is given by
Now we can apply series (4) to for , and we have
which is exactly the same solution as in [19].
Example 3
Let us consider the nonlinear time-fractional Fisher’s equation
The exact solution, for the special case , is given by
As in the previous examples, we can apply series (4) to obtain the solution for , and we get
which is totaly the same solution as in [20].
Example 4
Let us consider the following time-fractional initial boundary value problem:
where the boundary conditions are given in fractional terms.
Boundary value problem (17)-(18), for the special case , becomes as follows:
and its analytic solution is obtained as follows:
Now we can apply series (4) to for , and we have
which is exactly the same solution as in [21].
Example 5
Let us consider the following space-fractional initial boundary value problem:
The exact solution, for the special case , is given by
Now we can apply series (9) to for , then we have
Example 6
Let us consider the following space and time-fractional initial boundary value problem:
The exact solution, for the special case and , is given by
Now we can apply the series (4)-(9) to for and , then we have
Example 7
Let us consider the following space and time-fractional initial boundary value problem:
The exact solution, for the special case and , is given by
Now we can apply the series (4)-(9) to for and , then we have
Figures 7-9 show the evolution results for the approximate solutions of problem (23)-(24) obtained for different values of α and β.
References
Oldham KB, Spanier J: The Fractional Calculus. Academic Press, New York; 1974.
Podlubny I: Fractional Differential Equations. Academic Press, San Diego; 1999.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam; 2006.
He JH: Nonlinear oscillation with fractional derivative and its applications. International Conference on Vibrating Engineering’98 1998, 288-291.
He JH: Some applications of nonlinear fractional differential equations and their approximations. Bull Sci Technol 1999, 15: 86-90.
He JH: Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput Methods Appl Mech Eng 1998, 167: 57-68. 10.1016/S0045-7825(98)00108-X
Metzler R, Klafter J: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys Rep 2000, 339: 1-77. 10.1016/S0370-1573(00)00070-3
Gazizov RK, Kasatkin AA, Lukashchuk SY: Group-invariant solutions of fractional differential equations. 1. In Nonlinear Science and Complexity. 1st edition. Edited by: Tenreiro Machado JA, Luo ACJ, Barbosa RS, Silva MF, Figueiredo LB. Springer, Dordrecht; 2011:51-61.
Huang F, Liu F: The time-fractional diffusion equation and fractional advection-dispersion equation. ANZIAM J. 2005, 46: 1-14.
Huang F, Liu F: The fundamental solution of the space-time fractional advection-dispersion equation. J. Appl. Math. Comput. 2005, 18(2):339-350. 10.1007/BF02936577
Momani S: Non-perturbative analytical solutions of the space- and time-fractional Burgers equations. Chaos Solitons Fractals 2006, 28(4):930-937. 10.1016/j.chaos.2005.09.002
Odibat Z, Momani S: Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonlinear Sci. Numer. Simul. 2006, 1(7):15-27.
Das S: Solution of fractional vibration equation by the variational iteration method and modified decomposition method. Int. J. Nonlinear Sci. Numer. Simul. 2008., 9: Article ID 361
Momani S, Odibat Z: Numerical comparison of methods for solving linear differential equations of fractional order. Chaos Solitons Fractals 2007, 31(5):1248-1255. 10.1016/j.chaos.2005.10.068
Odibat Z, Momani S: Approximate solutions for boundary value problems of time-fractional wave equation. Appl. Math. Comput. 2006, 181(1):767-774. 10.1016/j.amc.2006.02.004
Yildirim A: An algorithm for solving the fractional nonlinear Schrödinger equation by means of the homotopy perturbation method. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10: 445-451.
Ganji ZZ, Ganji DD, Jafari H, Rostamian M: Application of the homotopy perturbation method to coupled system of partial differential equations with time fractional derivatives. Topol. Methods Nonlinear Anal. 2008., 31: Article ID 341
Hang X, Shi-Yun L, Xiang-Cheng Y: Analysis of nonlinear fractional partial differential equations with the homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14: 1152-1156. 10.1016/j.cnsns.2008.04.008
Saha RS, Bera RK: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 2000, 339: 1-77. 10.1016/S0370-1573(00)00070-3
Odibat Z, Momani S: Numerical methods for nonlinear partial differential equations of fractional order. Appl. Math. Model. 2008, 32: 28-39. 10.1016/j.apm.2006.10.025
El-Sayed AMA, Gaber M: The Adomian decomposition method for solving partial differential equations of fractal order in finite domains. Phys. Lett. A 2006, 359: 175-182. 10.1016/j.physleta.2006.06.024
Sheu LJ, Tam LM, Lao SK: Parametric analysis and impulsive synchronization of fractional-order Newton-Leipnik systems. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10: 33-44.
Xu C, Wu G, Feng JW, Zhang WQ: Synchronization between two different fractional-order chaotic systems. Int. J. Nonlinear Sci. Numer. Simul. 2008, 9: 89-95.
Yildirim A: Homotopy perturbation method for solving the space-time fractional advection-dispersion equation. Adv. Water Resour. 2009, 32: 1711-1716. 10.1016/j.advwatres.2009.09.003
Acknowledgements
Dedicated to Professor Hari M Srivastava.
The research was supported by parts by the Scientific and Technical Research Council of Turkey (TUBITAK).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read, checked and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Demir, A., Erman, S., Özgür, B. et al. Analysis of fractional partial differential equations by Taylor series expansion. Bound Value Probl 2013, 68 (2013). https://doi.org/10.1186/1687-2770-2013-68
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-68