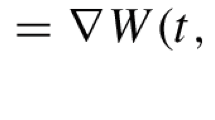Infinitely many periodic solutions for subquadratic second-order Hamiltonian systems

Abstract

In this paper, we investigate the existence of infinitely many periodic solutions for a class of subquadratic nonautonomous second-order Hamiltonian systems by using the variant fountain theorem.

1 Introduction

Consider the second-order Hamiltonian systems

$$\{\begin{array}{c}\ddot{u}(t)+{\mathrm{\nabla }}_{u}W(t,u)=0,\mathrm{\forall }t\in \mathbb{R},\hfill \\ u(0)=u(T),\dot{u}(0)=\dot{u}(T),T>0,\hfill \end{array}$$

(1.1)

where $W(t,u)$ is also T-periodic and satisfies the following assumption (A):

• (A) $W(t,u)$ is measurable in t for all $u\in {\mathbb{R}}^N$, continuously differentiable in u for a.e. $t\in [0,T]$ and there exist $a\in C(R^{+},R^{+})$ and $b\in L^1([0,T],R^{+})$ such that

  $$|W(t,u)|\le a(|u|)b(t),|{\mathrm{\nabla }}_{u}W(t,u)|\le a(|u|)b(t)$$

for all $u\in {\mathbb{R}}^N$ and a.e. $t\in [0,T]$.

Here and in the sequel, $〈\cdot ,\cdot 〉$ and $|\cdot |$ always denote the standard inner product and the norm in ${\mathbb{R}}^N$ respectively.

There have been many investigations on the existence and multiplicity of periodic solutions for Hamiltonian systems via the variational methods (see [1–7] and the references therein). In [6], Zhang and Liu studied the asymptotically quadratic case of $W(t,u)=\frac{1}{2}〈U(t)u,u〉+W_1(t,u)$ under the following assumptions:

(AQ₁) $W_1(t,u)\ge 0$ for all $(t,u)\in [0,T]\times {\mathbb{R}}^N$, and there exist constants $\mu \in (0,2)$ and $R_1>0$ such that

$$〈{\mathrm{\nabla }}_u{W}_1(t,u),u〉\le \mu W_1(t,u),\mathrm{\forall }t\in [0,T]\text{ and }|u|\ge R_1;$$

(AQ₂) ${lim}_{|u|\to 0}\frac{W_1(t,u)}{{|u|}^2}=\mathrm{\infty }$ uniformly for $t\in [0,T]$, and there exist constants $c_2,R_2>0$ such that

$$W_1(t,u)\le c_2|u|,\mathrm{\forall }t\in [0,T]\text{ and }|u|\le R_2;$$

(AQ₃) $lim{inf}_{|u|\to \mathrm{\infty }}\frac{W_1(t,u)}{|u|}\ge d>0$ uniformly for $t\in [0,T]$.

They obtained the existence of infinitely many periodic solutions of (1.1) provided $W_1(t,u)$ is even in u (see Theorem 1.1 of [6]).

The subquadratic condition (AQ₁) is widely used in the investigation of nonlinear differential equations. This condition was weakened by some researchers; see, for example, [4] of Jiang and Tang. This paper considers the case of $U(t)\equiv 0$, then $W(t,u)=W_1(t,u)$. Motivated by [4] and [6], we replace (AQ₁) with the following condition:

(${\mathrm{AQ}}_1^{\prime }$) $W(t,u)\ge 0$ for all $(t,u)\in [0,T]\times {\mathbb{R}}^N$, and

The condition (${\mathrm{AQ}}_1^{\prime }$) implies that for some constant $R_1^{\prime }>0$,

$$〈{\mathrm{\nabla }}_{u}W(t,u),u〉\le 2W(t,u),\mathrm{\forall }t\in [0,T]\text{ and }|u|\ge R_1^{\prime }.$$

(1.2)

By the assumption (A) and the condition (${\mathrm{AQ}}_1^{\prime }$), for any $ϵ>0$, there exists a $\delta >0$ such that

$$W(t,u)\le ϵ{|u|}^2+\underset{s\in [0,\delta ]}{max}a(s)b(t),$$

(1.3)

for $\mathrm{\forall }u\in {\mathbb{R}}^N$ and a.e. $t\in [0,T]$.

Meanwhile, we weaken the condition (AQ₃) to (${\mathrm{AQ}}_3^{\prime }$) as follows:

(${\mathrm{AQ}}_3^{\prime }$) There exists a constant $\varrho \in (0,1]$ such that

$$\underset{|u|\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\frac{W(t,u)}{{|u|}^{\varrho }}\ge d>0\text{uniformly for }t\in [0,T].$$

Then our main result is the following theorem.

Theorem 1.1 Assume that (${\mathrm{AQ}}_1^{\prime }$), (AQ₂), (${\mathrm{AQ}}_3^{\prime }$) hold and $W(t,u)$ is even in u. Then (1.1) possesses infinitely many solutions.

Remark The conditions (AQ₁) and (AQ₃) are stronger than (${\mathrm{AQ}}_1^{\prime }$) and (${\mathrm{AQ}}_3^{\prime }$). Then Theorem 1.1 above is different from Theorem 1.1 of [6].

2 Preliminaries

In this section, we establish the variational setting for our problem and give the variant fountain theorem. Let $E=H_T^1$ be the usual Sobolev space with the inner product

$${〈u,v〉}_E={\int }_0^T〈u(t),v(t)〉dt+{\int }_0^T〈\dot{u}(t),\dot{v}(t)〉dt.$$

We define the functional on E by

$$\mathrm{\Phi }(u)=\frac{1}{2}{\int }_0^T{|\dot{u}|}^{2}dt-\mathrm{\Psi }(u),$$

where $\mathrm{\Psi }(u)={\int }_0^{T}W(t,u(t))dt$. Then Φ and Ψ are continuously differentiable and

$$〈{\mathrm{\Phi }}^{\prime }(u),v〉={\int }_0^T〈\dot{u},\dot{v}〉dt-{\int }_0^T〈{\mathrm{\nabla }}_{u}W(t,u),v〉dt.$$

Define a self-adjoint linear operator $\mathcal{B}:L^2([0,T];{\mathbb{R}}^N)\to L^2([0,T];{\mathbb{R}}^N)$ by

$${\int }_0^T〈\mathcal{B}u,v〉dt={\int }_0^T〈\dot{u}(t),\dot{v}(t)〉dt$$

with the domain $D(\mathcal{B})=E$. Then ℬ has a sequence of eigenvalues ${\sigma }_k=\frac{4k^2{\pi }^2}{T^2}$ ($k=0,1,2,\dots$). Let ${\{e_j\}}_{j=0}^{+\mathrm{\infty }}$ be the system of eigenfunctions corresponding to ${\{{\sigma }_j\}}_{j=0}^{+\mathrm{\infty }}$, it forms an orthogonal basis in $L^2$. Denote by $E^{+}=\{u\in E|{\int }_0^{T}u(t)dt=0\}$, $E^0={\mathbb{R}}^N$, it is well known that

and E possesses orthogonal decomposition $E=E^0\oplus E^{+}$. For $u\in E$, we have

$$u=u^0+u^{+}\in E^0\oplus E^{+}.$$

We can define on E a new inner product and the associated norm by

$${〈u,v〉}_0={〈\mathcal{B}{u}^{+},v^{+}〉}_{L^2}+{〈u^0,v^0〉}_{L^2},$$

and

$$\parallel u\parallel ={〈u,u〉}_0^{\frac{1}{2}}.$$

Therefore, Φ can be written as

$$\mathrm{\Phi }(u)=\frac{1}{2}{\parallel u^{+}\parallel }^2-\mathrm{\Psi }(u).$$

(2.1)

Direct computation shows that

$$\begin{array}{r}〈{\mathrm{\Psi }}^{\prime }(u),v〉={\int }_0^T〈{\mathrm{\nabla }}_{u}W(t,u),v〉dt,\\ 〈{\mathrm{\Phi }}^{\prime }(u),v〉={〈u^{+},v^{+}〉}_0-〈{\mathrm{\Psi }}^{\prime }(u),v〉\end{array}$$

(2.2)

for all $u,v\in E$ with $u=u^0+u^{+}$ and $v=v^0+v^{+}$ respectively. It is known that ${\mathrm{\Psi }}^{\prime }:E\to E$ is compact.

Denote by ${|\cdot |}_p$ the usual norm of $L^P$, then there exists a ${\tau }_p>0$ such that

$${|u|}_p\le {\tau }_p\parallel u\parallel ,\mathrm{\forall }u\in E.$$

(2.3)

We state an abstract critical point theorem founded in [8]. Let E be a Banach space with the norm $\parallel \cdot \parallel$ and $E=\overline{{⨁}_{j\in \mathbb{N}}{X}_j}$ with $dim{X}_j<\mathrm{\infty }$ for any $j\in \mathbb{N}$. Set $Y_k={⨁}_{j=1}^k{X}_j$ and $Z_k=\overline{{⨁}_{j=k}^{\mathrm{\infty }}{X}_j}$ . Consider the following $C^1$-functional ${\mathrm{\Phi }}_{\lambda }:E\to \mathbb{R}$ defined by

$${\mathrm{\Phi }}_{\lambda }(u):=A(u)-\lambda B(u),\lambda \in [1,2].$$

Theorem 2.1 [[8], Theorem 2.2]

Assume that the functional ${\mathrm{\Phi }}_{\lambda }$ defined above satisfies the following:

(T₁) ${\mathrm{\Phi }}_{\lambda }$ maps bounded sets to bounded sets uniformly for $\lambda \in [1,2]$, and ${\mathrm{\Phi }}_{\lambda }(-u)={\mathrm{\Phi }}_{\lambda }(u)$ for all $(\lambda ,u)\in [1,2]\times E$;

(T₂) $B(u)\ge 0$ for all $u\in E$, and $B(u)\to \mathrm{\infty }$ as $\parallel u\parallel \to \mathrm{\infty }$ on any finite-dimensional subspace of E;

(T₃) There exist ${\rho }_k>r_k>0$ such that

$${\alpha }_k(\lambda ):=\underset{u\in Z_k,\parallel u\parallel ={\rho }_k}{inf}{\mathrm{\Phi }}_{\lambda }(u)\ge 0>{\beta }_k(\lambda ):=\underset{u\in Y_k,\parallel u\parallel =r_k}{max}{\mathrm{\Phi }}_{\lambda }(u),\mathrm{\forall }\lambda \in [1,2]$$

and

$${\xi }_k(\lambda ):=\underset{u\in Z_k,\parallel u\parallel \le {\rho }_k}{inf}{\mathrm{\Phi }}_{\lambda }(u)\to 0\mathit{\text{as}}k\to \mathrm{\infty }\mathit{\text{uniformly for}}\lambda \in [1,2].$$

Then there exist ${\lambda }_n\to 1$, $u_{{\lambda }_n}\in Y_n$ such that

$${\mathrm{\Phi }}_{{\lambda }_n}^{\prime }{\mid }_{Y_n}(u_{{\lambda }_n})=0,{\mathrm{\Phi }}_{{\lambda }_n}(u_{{\lambda }_n})\to {\eta }_k\in [{\xi }_k(2),{\beta }_k(1)]\mathit{\text{as}}n\to \mathrm{\infty }.$$

Particularly, if $\{u_{{\lambda }_n}\}$ has a convergent subsequence for every k, then ${\mathrm{\Phi }}_1$ has infinitely many nontrivial critical points $\{u_k\}\subset E\setminus \{0\}$ satisfying ${\mathrm{\Phi }}_1(u_k)\to 0^{-}$ as $k\to \mathrm{\infty }$.

In order to apply this theorem to prove our main result, we define the functionals A, B and ${\mathrm{\Phi }}_{\lambda }$ on our working space E by

$$A(u)=\frac{1}{2}{\parallel u^{+}\parallel }^2,B(u)={\int }_0^{T}W(t,u)dt$$

(2.4)

and

$${\mathrm{\Phi }}_{\lambda }(u)=A(u)-\lambda B(u)=\frac{1}{2}{\parallel u^{+}\parallel }^2-\lambda {\int }_0^{T}W(t,u)dt$$

(2.5)

for all $u=u^0+u^{+}\in E=E^0+E^{+}$ and $\lambda \in [1,2]$. Then ${\mathrm{\Phi }}_{\lambda }\in C^1(E,\mathbb{R})$ for all $\lambda \in [1,2]$. Let $X_j=span\{e_j\}$, $j=0,1,2,\dots$ . Note that ${\mathrm{\Phi }}_1=\mathrm{\Phi }$, where Φ is the functional defined in (2.1).

3 Proof of Theorem 1.1

We firstly establish the following lemmas.

Lemma 3.1 Assume that (${\mathrm{AQ}}_1^{\prime }$) and (${\mathrm{AQ}}_3^{\prime }$) hold. Then $B(u)\ge 0$ for all $u\in E$ and $B(u)\to \mathrm{\infty }$ as $\parallel u\parallel \to \mathrm{\infty }$ on any finite-dimensional subspace of E.

Proof Since $W(t,u)\ge 0$, by (2.4), it is obvious that $B(u)\ge 0$ for all $u\in E$.

By the proof of Lemma 2.6 of [6], for any finite-dimensional subspace $Y\subset E$, there exists a constant $ϵ>0$ such that

$$m\left(\{t\in [0,T]:|u|\ge ϵ\parallel u\parallel \}\right)\ge ϵ,\mathrm{\forall }u\in Y\setminus \{0\},$$

(3.1)

where $m(\cdot )$ is the Lebesgue measure.

For the ϵ given in (3.1), let

$${\mathrm{\Lambda }}_u=\{t\in [0,T]:|u|\ge ϵ\parallel u\parallel \},\mathrm{\forall }u\in Y\setminus \{0\}.$$

Then $m({\mathrm{\Lambda }}_u)\ge ϵ$. By (${\mathrm{AQ}}_3^{\prime }$), there exists a constant $R_3>R_1^{\prime }$ such that

$$W(t,u)\ge d{|u|}^{\varrho }/2,\mathrm{\forall }t\in [0,T]\text{ and }|u|\ge R_3,$$

(3.2)

where $R_1^{\prime }$ is the constant given in (1.2). Note that

$$|u(t)|\ge R_3,\mathrm{\forall }t\in {\mathrm{\Lambda }}_u$$

(3.3)

for any $u\in Y$ with $\parallel u\parallel \ge R_3/ϵ$. Thus,

$$\begin{array}{rcl}B(u)& =& {\int }_0^{T}W(t,u)dt\ge {\int }_{{\mathrm{\Lambda }}_u}W(t,u)dt\ge {\int }_{{\mathrm{\Lambda }}_u}d{|u|}^{\varrho }/2dt\\ \ge & d{ϵ}^{\varrho }{\parallel u\parallel }^{\varrho }\cdot m({\mathrm{\Lambda }}_u)/2\ge d{ϵ}^{\varrho +1}{\parallel u\parallel }^{\varrho }/2\end{array}$$

for any $u\in Y$ with $\parallel u\parallel \ge R_3/ϵ$. This implies $B(u)\to \mathrm{\infty }$ as $\parallel u\parallel \to \mathrm{\infty }$ on Y. □

Lemma 3.2 Assume that (${\mathrm{AQ}}_1^{\prime }$), (AQ₂) and (${\mathrm{AQ}}_3^{\prime }$) hold. Then there exist a positive integer $k_1$ and two sequences $0<r_k<{\rho }_k\to 0$ as $k\to \mathrm{\infty }$ such that

(3.4)

(3.5)

and

$${\beta }_k(\lambda ):=\underset{u\in Y_k,\parallel u\parallel =r_k}{max}{\mathrm{\Phi }}_{\lambda }(u)<0,\mathrm{\forall }k\in \mathbb{N},$$

(3.6)

where $Y_k={⨁}_{j=0}^k{X}_j=span\{e_0,e_1,\dots ,e_k\}$ and $Z_k=\overline{{⨁}_{j=k}^{\mathrm{\infty }}{X}_j}=\overline{span\{e_k,e_{k+1},\dots \}}$ for all $k\in \mathbb{N}$.

Proof Comparing this lemma with Lemma 2.7 of [6], we find that these two lemmas have the same condition (AQ₂) which is the key in the proof of Lemma 2.7 of [6]. We can prove our lemma by using the same method of [6], so the details are omitted. □

Now it is the time to prove our main result Theorem 1.1.

Proof of Theorem 1.1 By virtue of (1.3), (2.3) and (2.5), ${\mathrm{\Phi }}_{\lambda }$ maps bounded sets to bounded sets uniformly for $\lambda \in [1,2]$. Obviously, ${\mathrm{\Phi }}_{\lambda }(-u)={\mathrm{\Phi }}_{\lambda }(u)$ for all $(\lambda ,u)\in [1,2]\times E$ since $W(t,u)$ is even in u. Consequently, the condition (T₁) of Theorem 2.1 holds. Lemma 3.1 shows that the condition (T₂) holds, whereas Lemma 3.2 implies that the condition (T₃) holds for all $k\ge k_1$, where $k_1$ is given there. Therefore, by Theorem 2.1, for each $k\ge k_1$, there exist ${\lambda }_n\to 1$ and $u_{{\lambda }_n}\in Y_n$ such that

$${\mathrm{\Phi }}_{{\lambda }_n}^{\prime }{\mid }_{Y_n}(u_{{\lambda }_n})=0,{\mathrm{\Phi }}_{{\lambda }_n}(u_{{\lambda }_n})\to {\eta }_k\in [{\xi }_k(2),{\beta }_k(1)]\text{as }n\to \mathrm{\infty }.$$

(3.7)

For the sake of notational simplicity, in the following we always set $u_n=u_{{\lambda }_n}$ for all $n\in \mathbb{N}$.

Step 1. We firstly prove that $\{u_n\}$ is bounded in E.

Since $\{u_n\}$ satisfies (3.7), one has

$$\underset{n\to \mathrm{\infty }}{lim}(〈{\mathrm{\Phi }}_{{\lambda }_n}^{\prime }{\mid }_{Y_n}(u_n),u_n〉-2{\mathrm{\Phi }}_{{\lambda }_n}(u_n))=-2{\eta }_k.$$

More precisely,

$$\underset{n\to \mathrm{\infty }}{lim}{\int }_0^T(〈{\mathrm{\nabla }}_{u}W(t,u_n),u_n〉-2W(t,u_n))dt=2{\eta }_k.$$

(3.8)

Now, we prove that $\{u_n\}$ is bounded. Otherwise, without loss of generality, we may assume that

$$\parallel u_n\parallel \to \mathrm{\infty }\text{as }n\to \mathrm{\infty }.$$

Put $z_n=\frac{u_n}{\parallel u_n\parallel }$, we have $\parallel z_n\parallel =1$. Going to a subsequence if necessary, we may assume that

$$z_n\rightharpoonup z\text{in }E,z_n\to z\text{in }{L}^2\text{and}{z}_n(t)\to z(t)\text{for a.e. }t\in [0,T].$$

By (1.3), we have

$$\begin{array}{rcl}{\mathrm{\Phi }}_{{\lambda }_n}(u_n)& =& \frac{1}{2}{\parallel u_n^{+}\parallel }^2-{\lambda }_n{\int }_0^{T}W(t,u_n)dt\\ \ge & \frac{1}{2}{\parallel u_n\parallel }^2-\frac{1}{2}{\parallel u_n^0\parallel }^2-{\lambda }_n(ϵ{\int }_0^T{|u_n|}^{2}dt+\underset{s\in [0,\delta ]}{max}a(s){\int }_0^{T}b(t)dt)\\ \ge & \frac{1}{2}{\parallel u_n\parallel }^2-(\frac{1}{2}+{\lambda }_nϵ){\int }_0^T{|u_n|}^{2}dt-{\lambda }_n{c}_1,\end{array}$$

where $c_1={max}_{s\in [0,\delta ]}a(s){\int }_0^{T}b(t)dt$. Therefore, one obtains

$$\begin{array}{rcl}\frac{{\mathrm{\Phi }}_{{\lambda }_n}(u_n)}{{\parallel u_n\parallel }^2}& \ge & \frac{1}{2}-(\frac{1}{2}+{\lambda }_nϵ){\int }_0^T{\left(\frac{|u_n|}{\parallel u_n\parallel }\right)}^{2}dt-\frac{{\lambda }_n{c}_1}{{\parallel u_n\parallel }^2}\\ =& \frac{1}{2}-(\frac{1}{2}+{\lambda }_nϵ){\parallel z_n\parallel }_2^2-\frac{{\lambda }_n{c}_1}{{\parallel u_n\parallel }^2}.\end{array}$$

Passing to the limit in the inequality, by using ${\mathrm{\Phi }}_{{\lambda }_n}(u_n)\to {\eta }_k$ and ${\lambda }_n\to 1$ as $n\to \mathrm{\infty }$, we obtain

$$\frac{1}{2}-(\frac{1}{2}+ϵ){\parallel z\parallel }_2^2\le 0.$$

Thus, $z\ne 0$ on a subset Ω of $[0,T]$ with positive measure.

By (1.2), we have

$$〈{\mathrm{\nabla }}_{u}W(t,u),u〉-2W(t,u)\le 0,\mathrm{\forall }t\in [0,T]\text{ and }|u|\ge R_1^{\prime },$$

and by the assumption (A), we obtain

$$〈{\mathrm{\nabla }}_{u}W(t,u),u〉-2W(t,u)\le c_{3}b(t),\text{for all }|u|\le R_1^{\prime }\text{ and a.e. }t\in [0,T],$$

where $c_3=(2+R_1^{\prime }){max}_{[0,R_1^{\prime }]}a(s)$. So, we get

$$〈{\mathrm{\nabla }}_{u}W(t,u),u〉-2W(t,u)\le c_{3}b(t)$$

for all $u\in {\mathbb{R}}^N$ and a.e. $t\in [0,T]$. Hence,

An application of Fatou’s lemma yields

$${\int }_{\mathrm{\Omega }}(〈{\mathrm{\nabla }}_{u}W(t,u_n),u_n〉-2W(t,u_n))dt\to -\mathrm{\infty }\text{as }n\to \mathrm{\infty },$$

which is a contradiction to (3.8).

Step 2. We prove that $\{u_n\}$ has a convergent subsequence in E.

Since $\{u_n\}$ is bounded in E, E is reflexible and $dim{E}^0<\mathrm{\infty }$, without loss of generality, we assume

$$u_n^0\to u_0^0,u_n^{+}\rightharpoonup u_0^{+}\text{and}{u}_n\rightharpoonup u_0\text{as }n\to \mathrm{\infty }$$

(3.9)

for some $u_0=u_0^0+u_0^{+}\in E=E^0\oplus E^{+}$.

Note that

$$0={\mathrm{\Phi }}_{{\lambda }_n}^{\prime }{\mid }_{Y_n}(u_n)=u_n^{+}-{\lambda }_n{P}_n{\mathrm{\Psi }}^{\prime }(u_n),\mathrm{\forall }n\in \mathbb{N},$$

where $P_n:E\to Y_n$ is the orthogonal projection for all $n\in \mathbb{N}$, that is,

$$u_n^{+}={\lambda }_n{P}_n{\mathrm{\Psi }}^{\prime }(u_n),\mathrm{\forall }n\in \mathbb{N}.$$

(3.10)

In view of the compactness of ${\mathrm{\Psi }}^{\prime }$ and (3.9), the right-hand side of (3.10) converges strongly in E and hence $u_n^{+}\to u_0^{+}$ in E. Together with (3.9), we have $u_n\to u_0$ in E.

Now, from the last assertion of Theorem 2.1, we know that $\mathrm{\Phi }={\mathrm{\Phi }}_1$ has infinitely many nontrivial critical points. The proof is completed. □