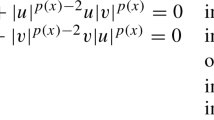Global solutions to a class of nonlinear damped wave operator equations

Abstract

This study investigates the existence of global solutions to a class of nonlinear damped wave operator equations. Dividing the differential operator into two parts, variational and non-variational structure, we obtain the existence, uniformly bounded and regularity of solutions.

Mathematics Subject Classification 2000: 35L05; 35A01; 35L35.

1 Introduction

In recent years, there have been extensive studies on well-posedness of the following nonlinear variational wave equation with general data:

$$\left\{\begin{array}{cc}{{\partial }_t}^{2}u-c\left(u\right){\partial }_x\left(c\left(u\right){\partial }_{x}u\right)=0\hfill & \mathsf{\text{in}}\left(0,\infty \right)\times \mathbf{R},\hfill \\ u{|}_{t=0}=u_0\hfill & \mathsf{\text{on}}\mathbf{R},\hfill \\ {\partial }_{t}u{|}_{t=0}=u_1\hfill & \mathsf{\text{on}}\mathbf{R},\hfill \end{array}\right.$$

(1.1)

where c(·) is given smooth, bounded, and positive function with c'(·) ≥ 0 and c'(u₀) > 0,u₀ ∈ H¹(R),u₁(x) ∈ L²(R). Equation (1.1) appears naturally in the study for liquid crystals [1–4]. In addition, Chang et al. [5], Su [6] and Kian [7] discussed globally Lipschitz continuous solutions to a class one dimension quasilinear wave equations

$$\left\{\begin{array}{c}{u}_{tt}-{\left(p\left(\rho \left(x\right),u_x\right)\right)}_x=\rho \left(x\right)h\left(\rho \left(x\right),u,u_x\right),\hfill \\ u\left(x,0\right)=u_0\left(x\right),\hfill \\ u_t\left(x,0\right)={\omega }_0\left(x\right),\hfill \end{array}\right.$$

(1.2)

where (x,t) ∈ R × R⁺, u₀(x),ω₀(x) ∈ R. Furthermore, Nishihara [8] and Hayashi [9] obtained the global solution to one dimension semilinear damped wave equation

$$\left\{\begin{array}{c}{u}_{tt}+u_t-u_{xx}=f\left(u\right),\left(t,x\right)\in {\mathbf{R}}^{+}\times {\mathbf{R}}^{+}\hfill \\ \left(u,u_t\right)\left(0,x\right)=\left(u_0,u_1\right)\left(x\right).\hfill \end{array}\right.$$

(1.3)

Ikehata [10] and Vitillaro [11] proved global existence of solutions for semilinear damped wave equations in R^Nwith noncompactly supported initial data or in the energy space, in where the nonlinear term f(u) = |u|^por f(u) = 0 is too special; some authors [12–14] discussed the regularity of invariant sets in semilinear wave equation, but they didn't refer to any the initial value condition of it. Unfortunately, it is difficulty to classify a class wave operator equations, since the differential operator structure is too complex to identify whether have variational property. Our aim is to classify a class of nonlinear damped wave operator equations in order to research them more extensively and go beyond the results of [12].

In this article, we are interested in the existence of global solutions of the following nonlinear damped wave operator equations:

$$\left\{\begin{array}{cc}\frac{d^{2}u}{d{t}^2}+k\frac{du}{dt}=G\left(u\right),\hfill & k>0\hfill \\ u\left(x,0\right)=\phi \left(x\right),\hfill \\ u_t\left(x,0\right)=\psi \left(x\right),\hfill \end{array}\right.$$

(1.4)

where $G:X_2\times {\mathbf{R}}^{+}\to X_1^{*}$ is a mapping, X₂ ⊂ X₁, X₁, X₂ are Banach spaces and $X_1^{*}$ is the dual spaces of X₁, R⁺ = [0, ∞), u = u(x,t). If k > 0, (1.4) is called damped wave equation. We obtain the existence, uniformly bounded and regularity of solutions by dividing the differential operator G(u) into two parts, variational and non-variational structure.

2 Preliminaries

First we introduce a sequence of function spaces:

$$\left\{\begin{array}{c}X\subset H_2\subset X_2\subset X_1\subset H,\hfill \\ X_2\subset H_1\subset H,\hfill \end{array}\right.$$

(2.1)

where H, H₁, H₂ are Hilbert spaces, X is a linear space, X₁, X₂ are Banach spaces and all inclusions are dense embeddings. Suppose that

$$\left\{\begin{array}{c}L:X\to X_1\mathsf{\text{is}}\mathsf{\text{one}}\mathsf{\text{to}}\mathsf{\text{one}}\mathsf{\text{dense}}\mathsf{\text{linear}}\mathsf{\text{operator}},\hfill \\ {〈Lu,v〉}_H={〈u,v〉}_H,\forall u,v\in X.\hfill \end{array}\right.$$

(2.2)

In addition, the operator L has an eigenvalue sequence

$$L{e}_k={\lambda }_k{e}_k,\left(k=1,2,...\right)$$

(2.3)

such that {e _k } ⊂ X is the common orthogonal basis of H and H₂. We investigate the existence of global solutions of the Equation (1.4), so we need define its solution. Firstly, in Banach space X, introduce

$$L^p\left(\left(0,T\right),X\right)=\left\{u:\left(0,T\right)\to X|\underset{0}{\overset{T}{\int }}{∥u∥}^{p}dt<\infty \right\},$$

where p = (p₁, p₂,..., p _m ),p _i ≥ 1(1 ≤ i ≤ m),

$${∥u∥}^p=\sum _{k=1}^m{\left|u\right|}_k^{p_k},$$

where | · | _k is semi-norm in X, and ${∥\cdot ∥}_X={\sum }_{i=1}^m{\left|\cdot \right|}_i$. Similarily, we can define

$$W^{1,p}\left(\left(0,T\right),X\right)=\left\{u:\left(0,T\right)\to X|u,u^{\prime }\in L^p\left(\left(0,T\right),X\right)\right\}.$$

Let $L_{\mathsf{\text{loc}}}^p\left(\left(0,\infty \right),X\right)=\left\{u\left(t\right)\in X|u\in L^p\left(\left(0,T\right),X\right),\forall T>0\right\}.$.

Definition 2.1. Set (φ, ψ) ∈ X₂ × H₁, $u\in W_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\right)\bigcap L_{\mathsf{\text{loc}}}^{\infty }\left(\left(0,\infty \right),X_2\right)$ is called a globally weak solution of (1.4), if for ∀v ∈ X₁, it has

$${〈u_t,v〉}_H+k{〈u,v〉}_H=\underset{0}{\overset{t}{\int }}〈Gu,v〉dt+k{〈\phi ,v〉}_H+{〈\psi ,v〉}_H.$$

(2.4)

Definition 2.2. Let Y₁,Y₂ be Banach spaces, the solution u(t, φ, ψ) of (1.4) is called uniformly bounded in Y₁ × Y₂, if for any bounded domain Ω₁ × Ω₂⊂Y₁ × Y₂, there exists a constant C which only depends the domain Ω₁ × Ω₂, such that

$${∥u∥}_{Y_1}+{∥u_t∥}_{Y_2}\le C,\forall \left(\phi ,\psi \right)\in {\mathrm{\Omega }}_1\times {\mathrm{\Omega }}_2\mathsf{\text{and}}t\ge 0.$$

Definition 2.3. A mapping $G:X_2\to X_1^{*}$ is called weakly continuous, if for any sequence {u _n } ⊂ X₂, u _n ⇀ u₀ in X₂,

$$\underset{n\to \infty }{\mathsf{\text{lim}}}〈G\left(u_n\right),v〉=〈G\left(u_0\right),v〉,\forall v\in X_1.$$

Lemma 2.1. [15]Let H₂, H be Hilbert spaces, and H₂ ⊂ H be a continuous embedding. Then there exists a orthonormal basis {e _k } of H, and also is one orthogonal basis of H₂.

Proof. Let I : H₂ → H be imbedded. According to assume I is a linear compact operator, we define the mapping A : H₂ → H as follows

$${〈Au,v〉}_{H_2}={〈Iu,v〉}_H={〈u,v〉}_H,\forall v\in H_2.$$

obviously, A : H₂ → H₂ is linear symmetrical compact operator and positive definite. Therefore, A has a complete eigenvalue sequence {λ _k } and eigenvector sequence$\left\{{ẽ}_k\right\}\subset H_2$ such that

$$A{ẽ}_k={\lambda }_k{ẽ}_k,k=1,2,...,$$

and $\left\{{ẽ}_k\right\}$ is orthogonal basis of H₂. Hence

$${〈{ẽ}_i,{ẽ}_j〉}_H={〈A{ẽ}_i,{ẽ}_j〉}_{H_2}={\lambda }_i{〈{ẽ}_i,{ẽ}_j〉}_{H_2}=0,\mathsf{\text{if}}i\ne j.$$

it implies $\left\{{ẽ}_i\right\}$ is also orthogonal sequence of H. Since H₂ ⊂ H is dense, $\left\{{ẽ}_i\right\}$ is also orthogonal sequence of H, so $\left\{e_i\right\}=\left\{{ẽ}_i/{∥{ẽ}_i∥}_H\right\}$ is norm orthogonal basis of H. The proof is completed.

Now, we introduce an important inequality

Lemma 2.2. [16] (Gronwall inequality) Let x(t), y(t), z(t) be real function on [a, b], where x(t) ≥ 0,∀a ≤ t ≤ b, z(t) ∈ C[a, b], y(t) is differentiable on [a, b]. If the inequality as follows is hold

$$z\left(t\right)\le y\left(t\right)+\underset{a}{\overset{t}{\int }}x\left(\tau \right)z\left(\tau \right)d\tau ,a\le t\le b,$$

(2.5)

then

$$z\left(t\right)\le y\left(a\right)e^{{\int }_a^{t}x\left(s\right)ds}+\underset{a}{\overset{t}{\int }}{e}^{{\int }_a^{t}x\left(\tau \right)}\frac{dy}{ds}ds.$$

(2.6)

3 Main results

Suppose that $G=A+B:X_2\times {\mathbf{R}}^{+}\to X_1^{*}$. Throughout of this article, we assume that

• (i) There exists a function F ∈ C ¹ : X ₂ → R ¹ such that

  $$〈Au,Lv〉=〈-DF\left(u\right),v〉,\forall u,v\in X$$

  (3.1)

• (ii) Function F is coercive, if

  $$F\left(u\right)\to \infty \iff {∥u∥}_{X_2}\to \infty$$

  (3.2)

• (iii) B as follows

  $$\left|〈Bu,Lv〉\right|\le C_{1}F\left(u\right)+C_2{∥v∥}_{H_1}^2,\forall u,v\in X$$

  (3.3)

for some $g\in L_{\mathsf{\text{loc}}}^1\left(0,\infty \right)$.

Theorem 3.1. Set$G:X_2\times {\mathbf{R}}^{+}\to X_1^{*}$is weakly continuous, (φ, ψ) ∈ X₂ × H₁, then we obtain the results as follows:

(1) If G = A satisfies the assumption (i) and (ii), then there exists a globally weak solution of (1.4)

$$u\in W_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\bigcap \underset{\mathsf{\text{loc}}}{\overset{\infty }{L}}\left(\left(0,\infty \right),X_2\right)\right)$$

and u is uniformly bounded in X₂ × H₁;

(2) If G = A + B satisfies the assumption (i), (ii) and (iii), then there exists a globally weak solution of (1.4)

$$u\in W_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\right)\bigcap \underset{\mathsf{\text{loc}}}{\overset{\infty }{L}}\left(\left(0,\infty \right),X_2\right);$$

(3) Furthermore, if G = A + B satisfies

$$\left|〈Gu,v〉\right|\le \frac{1}{2}{∥v∥}_H^2+CF\left(u\right)+g\left(t\right)$$

(3.4)

for some$g\in L_{\mathsf{\text{loc}}}^1\left(0,\infty \right)$, then$u\in W_{\mathsf{\text{loc}}}^{2,2}\left(\left(0,\infty \right),H\right)$.

Proof. Let {e _k } ⊂ X be the public orthogonal basis of H and H₂, satisfies (2.3).

Note

$$\left\{\begin{array}{c}{X}_n=\left\{\sum _{i=1}^n{\alpha }_i{e}_i|{\alpha }_i\in {\mathbf{R}}^1\right\},\hfill \\ {\tilde{X}}_n=\left\{\sum _{j=1}^n{\beta }_j\left(t\right)e_j|{\beta }_j\in C^2\left[0,\infty \right)\right\}.\hfill \end{array}\right.$$

(3.5)

From the assumption, we know $L{X}_n=X_n,L\widetilde{X_n}=\widetilde{X_n}$, apply the Galerkin method to make truncate in $\widetilde{X_n}$:

$$\left\{\begin{array}{cc}\frac{d^2{u}_i}{d{t}^2}+k\frac{d{u}_i}{dt}=〈G\left(u_n\right),e_i〉,\hfill & 1\le i\le n\hfill \\ u_i\left(x,0\right)={〈\phi ,e_i〉}_H,\hfill \\ {u^{\prime }}_i\left(x,0\right)={〈\psi ,e_i〉}_H\hfill \end{array}\right.$$

(3.6)

there exists $u_n={\sum }_{i=1}^n{u}_i\left(t\right)e_i\in C^2\left(\left(0,\infty \right),X_n\right)$ for any $v\in \widetilde{X_n}$ satisfies

$$\underset{0}{\overset{t}{\int }}{〈\frac{d^2{u}_n}{d{t}^2}+k\frac{d{u}_n}{dt},v〉}_{H}dt=\underset{0}{\overset{t}{\int }}〈G{u}_n,v〉dt$$

(3.7)

for any v ∈ X _n , it yields that

$${〈\frac{d{u}_n}{dt},v〉}_H+k{〈u_n,v〉}_H=\underset{0}{\overset{t}{\int }}〈G{u}_n,v〉dt+k{〈\phi ,v〉}_H+{〈\psi ,v〉}_H$$

(3.8)

• (1) If $G=A,u_n\in \widetilde{X_n}$ substitute $v=\frac{d}{dt}L{u}_n$ into (3.7), we get

  $$\underset{0}{\overset{t}{\int }}{〈\frac{d^2{u}_n}{d{t}^2}+k\frac{d{u}_n}{dt},\frac{d}{dt}L{u}_n〉}_{H_1}dt=\underset{0}{\overset{t}{\int }}〈G{u}_n,\frac{d}{dt}L{u}_n〉dt$$

combine condition (2.2) with (3.1), we get

$$\begin{array}{c}\underset{0}{\overset{t}{\int }}\underset{\mathrm{\Omega }}{\int }\frac{d^2{u}_n}{d{t}^2}\frac{d{u}_n}{dt}dxdt+\underset{0}{\overset{t}{\int }}\underset{\mathrm{\Omega }}{\int }k\frac{d{u}_n}{dt}\frac{d{u}_n}{dt}dxdt+\underset{0}{\overset{t}{\int }}DF\left(u_n\right)\frac{d{u}_n}{dt}dxdt=0\\ \underset{0}{\overset{t}{\int }}\frac{1}{2}\frac{d}{dt}{∥\frac{d{u}_n}{dt}∥}_{H_1}^{2}dt+k\underset{0}{\overset{t}{\int }}{∥\frac{d{u}_n}{dt}∥}_{H_1}^{2}dt+\underset{0}{\overset{t}{\int }}\frac{d}{dt}F\left(u_n\right)dt=0\\ \frac{1}{2}{∥\frac{d{u}_n}{dt}∥}_{H_1}^2-\frac{1}{2}{∥{\psi }_n∥}_{H_1}^2+k\underset{0}{\overset{t}{\int }}{∥\frac{d{u}_n}{dt}∥}_{H_1}^{2}dt+F\left(u_n\right)-F\left({\phi }_n\right)=0\end{array}$$

consequently, we get

$$F\left(u_n\right)+\frac{1}{2}{∥{u^{\prime }}_n∥}_{H_1}^2+k\underset{0}{\overset{t}{\int }}{∥{u^{\prime }}_n∥}_{H_1}^{2}dt=F\left(u_n\right)+\frac{1}{2}{∥{\psi }_n∥}_{H_1}^2.$$

(3.9)

Assume φ ∈ H₂, combine(2.2)with(2.3), we know {e _n } is also the orthogonal basis of H₁, then φ _n → φ in H₂, ψ _n → ψ in H₁, owing to H₂ ⊂ X₂ is embedded, so

$$\left\{\begin{array}{c}{\phi }_n\to \phi in{X}_2\hfill \\ {\psi }_n\to \psi in{X}_1\hfill \end{array}\right.$$

(3.10)

due to the condition (3.6), from (3.9)and (3.10) we easily know

$$\left\{u_n\right\}\subset W_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\right)\bigcap \underset{\mathsf{\text{loc}}}{\overset{\infty }{L}}\left(\left(0,\infty \right),X_2\right)isbounded.$$

consequently, assume that

$$u_n\rightharpoonup u_{0}in{W}_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\right)\bigcap \underset{\mathsf{\text{loc}}}{\overset{\infty }{L}}\left(\left(0,\infty \right),X_2\right)a.e.t>0$$

i.e. u _n ⇀ u₀in X₂a.e. t > 0, and G is weakly continuous, so

$$\underset{n\to \infty }{\mathsf{\text{lim}}}〈G{u}_n,v〉=〈G{u}_0,v〉.$$

By (3.8), we have

$$\begin{array}{cc}\hfill \underset{n\to \infty }{\mathsf{\text{lim}}}\left[{〈\frac{d{u}_n}{dt}〉}_H+k{〈u_n,v〉}_H\right]& =\underset{n\to \infty }{\mathsf{\text{lim}}}\underset{0}{\overset{t}{\int }}〈G{u}_{n,}v〉dt+k{〈\phi ,v〉}_H+{〈\psi ,v〉}_H\hfill \\ \hfill {〈\frac{d{u}_0}{dt},v〉}_H+k{〈u_0,v〉}_H& =\underset{0}{\overset{t}{\int }}〈G{u}_0,v〉dt+k{〈\phi ,v〉}_H+{〈\psi ,v〉}_H\hfill \end{array}$$

it indicates for any $v\in {\bigcup }_{n=1}^{\infty }{X}_n\subset X_2$, it holds. Hence, for any v ∈ X₂, we have

$${〈\frac{d{u}_0}{dt},v〉}_H+k{〈u_0,v〉}_H=\underset{0}{\overset{t}{\int }}〈G{u}_0,v〉dt+k{〈\phi ,v〉}_H+{〈\psi ,v〉}_H.$$

(3.11)

Consequently, u₀ is a globally weak solution of (1.4).

Furthermore, by (3.9) and (3.10), for any R > 0, there exists a constant C such that if

$${∥\phi ∥}_{X_2}+{∥\psi ∥}_{H_1}\le R$$

(3.12)

then the weak solution u(t, φ, ψ) of (1.4) satisfies

$${∥u\left(t,\phi ,\psi \right)∥}_{X_2}+{∥u_t\left(t,\phi ,\psi \right)∥}_{H_1}\le C.\forall t\ge 0$$

(3.13)

Assume (φ,ψ) ∈ X₂ × H₁ satisfies (3.12), by H₂ ⊂ X₂ is dense. May fix φ _n ∈ H₂ such that

$${∥{\phi }_n∥}_{X_2}+{∥\psi ∥}_{H_1}\le R,\underset{n\to \infty }{\mathsf{\text{lim}}}{\phi }_n=\phi \mathsf{\text{in}}{X}_2$$

by (3.13), the solution {u(t, φ _n , ψ)} of (1.4) is bounded in $W_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\right)\bigcap L_{\mathsf{\text{loc}}}^{\infty }\left(\left(0,\infty \right),X_2\right)$ a.e. t > 0.

Therefore, assume u(t, φ _n , ψ) ⇀ u in $W_{\mathsf{\text{loc}}}^{1,\infty }\left(\left(0,\infty \right),H_1\right)\bigcap L_{\mathsf{\text{loc}}}^{\infty }\left(\left(0,\infty \right),X_2\right)$ then u(t) is a weak solution of (1.4), it satisfies uniformly bounded of (3.13). So the conclusion (1) is proved.

• (2) If $G=A+B,u_n\in \widetilde{X_n}$, substitute $v=\frac{d}{dt}L{u}_n$ into (3.7), we get

  $$\begin{array}{l}\underset{0}{\overset{t}{\int }}\left[{〈\frac{d^2{u}_n}{d{t}^2},\frac{d}{dt}L{u}_n〉}_{H_1}\right]+k{〈\frac{d{u}_n}{dt},\frac{d}{dt}L{u}_{n1}〉}_{H_1}dt\\ =\underset{0}{\overset{t}{\int }}\left[〈A{u}_n,\frac{d{u}_n}{dt}〉+〈B{u}_n,\frac{d{u}_n}{dt}〉\right]dt\end{array}$$

combine the condition (2.2) and (3.1), we have

$$\begin{array}{l}\underset{0}{\overset{t}{\int }}\underset{\Omega }{\int }\frac{d^2{u}_n}{d{t}^2}\frac{d{u}_n}{dt}dxdt+k\underset{0}{\overset{t}{\int }}\underset{\Omega }{\int }\frac{d{u}_n}{d{t}^2}\frac{d{u}_n}{dt}dxdt+\underset{0}{\overset{t}{\int }}〈DF\left(u_n\right)\frac{d{u}_n}{dt}〉dt\\ =\underset{0}{\overset{t}{\int }}〈B{u}_n,\frac{d{u}_n}{dt}〉dt\\ \underset{0}{\overset{t}{\int }}\frac{1}{2}\frac{d}{dt}{∥\frac{d{u}_n}{dt}∥}_{H_1}^{2}dt+k\underset{0}{\overset{t}{\int }}{∥\frac{d{u}_n}{dt}∥}_{H_1}^{2}dt+\underset{0}{\overset{t}{\int }}\frac{d}{dt}F\left(u_n\right)dt\\ =\underset{0}{\overset{t}{\int }}〈B{u}_n,\frac{d{u}_n}{dt}〉dt\\ \frac{1}{2}{∥{u^{\prime }}_n∥}_{H_1^2}-\frac{1}{2}{∥{\psi }_n∥}_{H_1}^2+k\underset{0}{\overset{t}{\int }}{∥{u^{\prime }}_n∥}_{H_1}^{2}dt+F\left(u_n\right)+F\left({\phi }_n\right)\\ =\underset{0}{\overset{t}{\int }}〈B{u}_n,\frac{d{u}_n}{dt}〉dt\end{array}$$

consequently, we have

$$F\left(u_n\right)+\frac{1}{2}{∥{u^{\prime }}_n∥}_{H_1}^2+k\underset{0}{\overset{t}{\int }}{∥{u^{\prime }}_n∥}_{H_1}^{2}dt=\underset{0}{\overset{t}{\int }}〈B{u}_n,\frac{d{u}_n}{dt}〉dt+F\left({\phi }_n\right)+\frac{1}{2}{∥{\psi }_n∥}_{H_1}^2$$

(3.14)

by the condition (3.3),(3.14)implies

$$F\left(u_n\right)+\frac{1}{2}{∥{u^{\prime }}_n∥}_{H_1}^2\le C\underset{0}{\overset{t}{\int }}\left[F\left(u_n\right)+\frac{1}{2}{∥{u^{\prime }}_n∥}_{H_1}^2\right]dt+f\left(t\right)$$

(3.15)

where $f\left(t\right)={\int }_0^{t}g\left(\tau \right)dt+\frac{1}{2}{∥\psi ∥}_{H_1}^2+{\mathsf{\text{sup}}}_{n}F\left({\phi }_n\right).$.

by Gronwall inequality [Lemma(2.2)], from (3.15) we easily know:

$$F\left(u_n\right)+\frac{1}{2}{∥{u^{\prime }}_n∥}_{H_1}^2\le f\left(0\right)e^{C^t}+\underset{0}{\overset{t}{\int }}{f}^{\prime }\left(\tau \right)e^{C\left(t-\tau \right)}d\tau$$

(3.16)

it implies that, for any 0 < T < ∞

$$\left\{u_n\right\}\subset W^{1,\infty }\left(\left(0,T\right),X_2\right)\bigcap L^{\infty }\left(\left(0,T\right),X_2\right)\mathsf{\text{is}}\mathsf{\text{bounded}}.$$

now, use the same way as (1), we can obtain the result (2).

• (3) If the condition (3.4) is hold, $u_n\in \widetilde{X_n}$, substitute $v=\frac{d^{2}u}{d{t}^2}$ into (3.7), we can get

  $$\underset{0}{\overset{t}{\int }}\left[{〈\frac{d^2{u}_n}{d{t}^2},\frac{d^2{u}_n}{d{t}^2}〉}_H+k{〈\frac{d{u}_n}{dt},\frac{d^2{u}_n}{d{t}^2}〉}_H\right]dt=\underset{0}{\overset{t}{\int }}〈G{u}_n,\frac{d^2{u}_n}{d{t}^2}〉dt$$

then

$$\begin{array}{l}\underset{0}{\overset{t}{\int }}{〈\frac{d^2{u}_n}{d{t}^2},\frac{d^2{u}_n}{d{t}^2}〉}_{H}dt+\frac{k}{2}\underset{0}{\overset{t}{\int }}\frac{d}{dt}{∥{u^{\prime }}_n\left(t\right)∥}_H^{2}dt\\ \le \underset{0}{\overset{t}{\int }}\left[\frac{1}{2}{∥{u^{″}}_n\left(t\right)∥}_H^2+CF\left(u_n\right)+g\left(t\right)\right]dt\\ \underset{0}{\overset{t}{\int }}{〈\frac{d^2{u}_n}{d{t}^2},\frac{d^2{u}_n}{d{t}^2}〉}_{H}dt+\frac{k}{2}{∥{u^{\prime }}_n∥}_H^2\\ \le \frac{k}{2}{∥{\psi }_n∥}_H^2+\underset{0}{\overset{t}{\int }}\left[\frac{1}{2}{∥\frac{d^2{u}_n}{d{t}^2}∥}_H^2+CF\left(u_n\right)+g\left(\tau \right)\right]d\tau \end{array}$$

by (3.16), it implies that

$$\underset{0}{\int }t{∥\frac{d^2{u}_n}{d{t}^2}∥}_H^{2}d\tau \le C,\left(C>0\right)$$

consequently, for any 0 < T < ∞

$$\left\{u_n\right\}\subset W^{2,2}\left(\left(0,T\right),H\right)\mathsf{\text{is}}\mathsf{\text{bounded}}.$$

it implies that u ∈ W^2,2((0,T), H), the main theorem (3.1) has been proved.