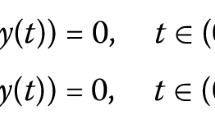Riemann-Liouville fractional integro-differential equations with fractional nonlocal integral boundary conditions

Abstract

This article investigates a boundary value problem of Riemann-Liouville fractional integro-differential equations with fractional nonlocal integral boundary conditions. Some new existence results are obtained by applying standard fixed point theorems.

2010 Mathematics Subject Classification: 26A33; 34A34; 34B15.

1 Introduction

In this article, we study the existence and uniqueness of solutions for the following nonlinear fractional integro-differential equation:

$$D^{\alpha }u\left(t\right)=f\left(t,u\left(t\right),\left(\varphi u\right)\left(t\right),\left(\psi u\right)\left(t\right)\right),t\in \left[0,T\right],\alpha \in \left(1\right.,\left.2\right],$$

(1.1)

subject to the boundary conditions of fractional order given by

$$D^{\alpha -2}u\left(0^{+}\right)=0,$$

(1.2)

$$D^{\alpha -1}u\left(0^{+}\right)=\nu I^{\alpha -1}u\left(\eta \right),0<\eta <T,\nu \mathsf{\text{is}}\mathsf{\text{a}}\mathsf{\text{constant}},$$

(1.3)

where D^αdenotes the Riemann-Liouville fractional derivative of order α, f: [0, T] × ℝ × ℝ × ℝ → ℝ is continuous, and

$$\left(\varphi x\right)\left(t\right)=\underset{0}{\overset{t}{\int }}\gamma \left(t,s\right)x\left(s\right)\mathsf{\text{d}}s,\left(\psi x\right)\left(t\right)=\underset{0}{\overset{t}{\int }}\delta \left(t,s\right)x\left(s\right)\mathsf{\text{d}}s,$$

with γ and δ being continuous functions on [0, T] × [0, T].

Boundary value problems for nonlinear fractional differential equations have recently been investigated by several researchers. As a matter of fact, fractional derivatives provide an excellent tool for the description of memory and hereditary properties of various materials and processes (see [1]) and make the fractional-order models more realistic and practical than the classical integer-order models. Fractional differential equations arise in many engineering and scientific disciplines, such as physics, chemistry, biology, economics, control theory, signal and image processing, biophysics, blood flow phenomena, aerodynamics, fitting of experimental data, etc. (see [1, 2]). For some recent development on the topic, (see [3–19] and references therein).

2 Preliminaries

Let us recall some basic definitions (see [20, 21]).

Definition 2.1 The Riemann-Liouville fractional integral of order α > 0 for a continuous function u: (0, ∞) → ℝ is defined as

$$I^{\alpha }u\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}\underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{\alpha -1}u\left(s\right)\mathsf{\text{d}}s,$$

provided the integral exists.

Definition 2.2 For a continuous function u: (0, ∞) → ℝ, the Riemann-Liouville derivative of fractional order α > 0, n = [α] + 1 ([α] denotes the integer part of the real number α) is defined as

$$D^{\alpha }u\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(n-\alpha \right)}{\left(\frac{1}{\mathsf{\text{d}}t}\right)}^n\underset{0}{\overset{t}{\int }}{\left(t-s\right)}^{n-\alpha -1}u\left(s\right)\mathsf{\text{d}}s={\left(\frac{\mathsf{\text{d}}}{\mathsf{\text{d}}t}\right)}^n{I}^{n-\alpha }u\left(t\right),$$

provided it exists.

For α < 0, we use the convention that D^αu = I^-αu. Also for β ∈ [0, α), it is valid that D^βI^au = I^α-βu.

Note that for λ >-1, λ ≠ α - 1, α - 2,..., α - n, we have

$$D^{\alpha }{t}^{\lambda }=\frac{\mathrm{\Gamma }\left(\lambda +1\right)}{\mathrm{\Gamma }\left(\lambda -\alpha +1\right)}{t}^{\lambda -\alpha },$$

and

$$D^{\alpha }{t}^{\alpha -i}=0,i=1,2,\dots ,n.$$

In particular, for the constant function u(t) = 1, we obtain

$$D^{\alpha }1=\frac{1}{\mathrm{\Gamma }\left(1-\alpha \right)}{t}^{-\alpha },\alpha \notin \mathbb{N}.$$

For α ∈ ℕ, we get, of course, D^α1 = 0 because of the poles of the gamma function at the points 0, -1, -2,....

For α > 0, the general solution of the homogeneous equation

$$D^{\alpha }u\left(t\right)=0$$

in C(0, T) ∩ L(0, T) is

$$u\left(t\right)=c_0{t}^{\alpha -n}+c_1{t}^{\alpha -n-1}+\cdots +c_{n-2}{t}^{\alpha -2}+c_{n-1}{t}^{\alpha -1},$$

where c _i , i = 1, 2,..., n - 1, are arbitrary real constants.

We always have D^αI^αu = u, and

$$I^{\alpha }{D}^{\alpha }u\left(t\right)=u\left(t\right)+c_0{t}^{\alpha -n}+c_1{t}^{\alpha -n-1}+\cdots +c_{n-2}{t}^{\alpha -2}+c_{n-1}{t}^{\alpha -1}.$$

To define the solution for the nonlinear problem (1.1) and (1.2)-(1.3), we consider the following linear equation

$$D^{\alpha }u\left(t\right)=\sigma \left(t\right),\alpha \in \left(1\right.,\left.2\right],t\in \left[0,T\right],T>0,$$

(2.1)

where σ ∈ C[0, T].

We define

$$A=\nu \underset{0}{\overset{\eta }{\int }}\frac{s^{\alpha -1}{\left(\eta -s\right)}^{\alpha -2}}{\mathrm{\Gamma }\left(\alpha -1\right)}\mathsf{\text{d}}s=\frac{\nu \mathrm{\Gamma }\mathsf{\text{(}}\alpha \mathsf{\text{)}}{\eta }^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)},$$

(2.2)

such that A ≠ Γ(α).

The general solution of (2.1) is given by

$$u\left(t\right)=c_1{t}^{\alpha -1}+c_0{t}^{\alpha -2}+I^{\alpha }\sigma \left(t\right),$$

(2.3)

with I^αthe usual Riemann-Liouville fractional integral of order α.

From (2.3), we have

$$D^{\alpha -1}u\left(t\right)=c_1\mathrm{\Gamma }\left(\alpha \right)+I^1\sigma \left(t\right),$$

(2.4)

$$D^{\alpha -2}u\left(t\right)=c_1\mathrm{\Gamma }\left(\alpha \right)t+c_0\mathrm{\Gamma }\left(\alpha -1\right)+I^2\sigma \left(t\right).$$

(2.5)

Using the conditions (1.2) and (1.3) in (2.4) and (2.5), we find that c₀ = 0 and

$$c_1=\frac{\nu }{\left[\mathrm{\Gamma }\left(\alpha \right)-A\right]}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{\alpha -2}}{\mathrm{\Gamma }\left(\alpha -1\right)}\left(\underset{0}{\overset{s}{\int }}\frac{{\left(s-x\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\sigma \left(x\right)\mathsf{\text{d}}x\right)\mathsf{\text{d}}s,$$

where A is defined by (2.2).

Substituting the values of c₀ and c₁ in (2.3), the unique solution of (2.1) subject to the boundary conditions (1.2)-(1.3) is given by

$$\begin{array}{ll}\hfill u\left(t\right)& =\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\sigma \left(s\right)\mathsf{\text{d}}s\\ +\frac{\nu t^{\alpha -1}}{\left[\mathrm{\Gamma }\left(\alpha \right)-A\right]}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{\alpha -2}}{\mathrm{\Gamma }\left(\alpha -1\right)}\left(\underset{0}{\overset{s}{\int }}\frac{{\left(s-x\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\sigma \left(x\right)\mathsf{\text{d}}x\right)\mathsf{\text{d}}s\\ =\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\sigma \left(s\right)\mathsf{\text{d}}s+\frac{\nu t^{\alpha -1}}{\left[\mathrm{\Gamma }\left(\alpha \right)-A\right]}{I}^{2\alpha -1}\sigma \left(\eta \right).\end{array}$$

(2.6)

3 Main results

Let $\mathcal{C}=C\left(\left[0,T\right],ℝ\right)$ denotes the Banach space of all continuous functions from [0, T] → ℝ endowed with the norm defined by ║u║ = sup{|u(t)|, t ∈ [0, T]}.

If u is a solution of (1.1) and (1.2)-(1.3), then

$$\begin{array}{ll}\hfill u\left(t\right)=& \underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\\ +{\nu }_1{t}^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s,\end{array}$$

where

$${\nu }_1=\frac{\nu }{\left[\mathrm{\Gamma }\left(\alpha \right)-A\right]}.$$

Define an operator $\mathcal{P}:\mathcal{C}\to \mathcal{C}$ as

$$\begin{array}{ll}\hfill \left(\mathcal{P}u\right)\left(t\right)=& \underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\\ +{\nu }_1{t}^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s,t\in \left[0,T\right].\end{array}$$

Observe that the problem (1.1) and (1.2)-(1.3) has solutions if and only if the operator equation $\mathcal{P}u=u$ has fixed points.

Lemma 3.1 The operator $\mathcal{P}$ is compact.

Proof

• (i) Let B be a bounded set in C[0, T]. Then, there exists a constant M such that |f(t,u(t), (φu)(t), (ψu)(t))| ≤ M, ∀u ∈ B, t∈[0, T]. Thus

  $$\begin{array}{ll}\hfill \left|\left(\mathcal{P}u\right)\left(t\right)\right|& \le M\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\mathsf{\text{d}}s+M\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\mathsf{\text{d}}s\\ \le M{T}^{\alpha -1}\left(\frac{T}{\mathrm{\Gamma }\left(\alpha +1\right)}+\frac{\left|{\nu }_1\right|{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right),\end{array}$$

which implies that

$$\left|\right|\left(\mathcal{P}u\right)\left|\right|\le M{T}^{\alpha -1}\left(\frac{T}{\mathrm{\Gamma }\left(\alpha +1\right)}+\frac{\left|{\nu }_1\right|{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right)<\infty .$$

Hence, $\mathcal{P}\left(\mathbf{B}\right)$ is uniformly bounded.

• (ii) For any t ₁, t ₂ ∈ [0, T], u ∈ B, we have

  $$\begin{array}{c}|\left(\mathcal{P}u\right)\left(t_1\right)-\left(\mathcal{P}u\right)\left(t_2\right)|\\ =\left|\underset{0}{\overset{t_1}{\int }}\frac{{\left(t_1-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\right.\\ -\underset{0}{\overset{t_2}{\int }}\frac{{\left(t_2-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\\ \left.+{\nu }_1\left(t_1^{\alpha -1}-t_2^{\alpha -1}\right)\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -s}}{\mathrm{\Gamma }\left(2\alpha -1\right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\right|\\ \le M\left(\left|\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}\underset{0}{\overset{t_1}{\int }}\left[{\left(t_1-s\right)}^{\alpha -1}-{\left(t_2-s\right)}^{\alpha -1}\right]\mathsf{\text{d}}s-\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}\underset{t_1}{\overset{t_2}{\int }}{\left(t_2-s\right)}^{\alpha -1}\mathsf{\text{d}}s\right|\right.\\ \left.+\left|{\nu }_1\left(t_1^{\alpha -1}-t_2^{\alpha -1}\right)\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -s}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\mathsf{\text{d}}s\right|\right)\to 0\mathsf{\text{as}}{t}_1\to t_2.\end{array}$$

Thus, $\mathcal{P}\left(\mathbf{B}\right)$ is equicontinuous. Consequently, the operator $\mathcal{P}$ is compact. This completes the proof.   □

We need the following known fixed point theorem to prove the existence of solutions for the problem at hand.

Theorem 3.1 ([22]) Let E be a Banach space. Assume that T: E → E be a completely continuous operator and the set V = {x ∈ E | x = μTx, 0 < μ < 1} be bounded.

Then, T has a fixed point in E.

Theorem 3.2 Assume that there exists a constant M > 0 such that

$$\left|f\left(t,u\left(t\right),\left(\varphi u\right)\left(t\right),\left(\psi u\right)\left(t\right)\right)\right|\le M,\forall t\in \left[0,T\right],u\in ℝ.$$

Then, the problem (1.1) and (1.2)-(1.3) has at least one solution on [0,T].

Proof We consider the set

$$V=\left\{u\in ℝ|u=\mu \mathcal{P}u,0<\mu <1\right\},$$

and show that the set V is bounded. Let u ∈ V, then $u=\mu \mathcal{P}u$, 0 < μ < 1. For any t ∈ [0, T], we have

$$\begin{array}{ll}\hfill \left|u\left(t\right)\right|\le & \mu \left[\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\right.\left|f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\right|\mathsf{\text{d}}s\\ \left.+\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\left|f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\right|\mathsf{\text{d}}s\right].\end{array}$$

As in part (i) of Lemma 3.1, we have

$$\parallel \left(\mathcal{P}u\right)\parallel \le M{T}^{\alpha -1}\left(\frac{T}{\mathrm{\Gamma }\left(\alpha +1\right)}+\frac{\left|{\nu }_1\right|{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right)<\infty .$$

This implies that the set V is bounded independently of μ ∈ (0,1). Using Lemma 3.1 and Theorem 3.1, we obtain that the operator $\mathcal{P}$ has at least a fixed point, which implies that the problem (1.1) and (1.2)-(1.3) has at least one solution. This completes the proof.

Theorem 3.3 Assume that

(A₁) there exist positive functions L₁(t), L₂(t), L₃(t) such that

$$\begin{array}{c}|f\left(t,u\left(t\right),\left(\varphi u\right)\left(t\right),\left(\psi u\right)\left(t\right)\right)-f\left(t,v\left(t\right),\left(\varphi v\right)\left(t\right),\left(\psi v\right)\left(t\right)\right)|\\ \le L_1\left(t\right)|u-v|+L_2\left(t\right)|\varphi u-\varphi v|+L_3\left(t\right)|\psi u-\psi v|,\forall t\in \left[0,1\right],u,v\in ℝ.\end{array}$$

(A₂) Λ = (ξ₁ + |ν₁|T^α-1ξ₂)(1 + γ₀ + δ₀) < 1, where

$$\begin{array}{ll}\hfill {\gamma }_0& =\underset{t\in \left[0,1\right]}{sup}\left|\underset{0}{\overset{t}{\int }}\gamma \left(t,s\right)\mathsf{\text{d}}s\right|,{\delta }_0=\underset{t\in \left[0,1\right]}{sup}\left|\underset{0}{\overset{t}{\int }}\delta \left(t,s\right)\mathsf{\text{d}}s\right|,\\ \hfill {\xi }_1& =\underset{t\in \left[0,T\right]}{sup}\left\{\left|I^q{L}_1\left(t\right)\right|,\left|I^q{L}_2\left(t\right)\right|,\left|I^q{L}_3\left(t\right)\right|\right\},\\ \hfill {\xi }_2& =max\left\{\left|I^{2\alpha -1}{L}_1\left(\eta \right)\right|,\left|I^{2\alpha -1}{L}_2\left(\eta \right)\right|,\left|I^{2\alpha -1}{L}_3\left(\eta \right)\right|\right\},\end{array}$$

Then the problem (1.1) and (1.2)-(1.3) has a unique solution on C[0, T].

Proof Let us set sup_{t∈[0, T]}|f(t,0,0,0)| = M, and choose

$$r\ge \frac{\epsilon M}{1-\mathrm{\Lambda }}.$$

Then we show that $\mathcal{P}{B}_r\subset B_r$, where $B_r=\left\{x\in \mathcal{C}:\parallel u\parallel \le r\right\}$. For x ∈ B _r , we have

$$\begin{array}{ll}\hfill \parallel \left(\mathcal{P}u\right)\left(t\right)\parallel & =\underset{t\in \left[0,T\right]}{sup}|\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\\ +{\nu }_1{t}^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s|\\ \le \underset{t\in \left[0,T\right]}{sup}\left(\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\left(|f\left(s,x\left(s\right),\left(\varphi x\right)\left(s\right),\left(\psi x\right)\left(s\right)\right)-f\left(s,0,0,0\right)\right.\right.|\\ +\left.\left|f\left(s,0,0,0\right)\right|\right)\mathsf{\text{d}}s\\ +\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -s}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\left(|f\left(s,x\left(s\right),\left(\varphi x\right)\left(s\right),\left(\psi x\right)\left(s\right)\right)-f\left(s,0,0,0\right)\right.\\ +\left.\left.\left|f\left(s,0,0,0\right)\right|\right)\mathsf{\text{d}}s\right)\\ \le \underset{t\in \left[0,T\right]}{sup}\left(\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\left(L_1\left(s\right)\left|x\left(s\right)\right|+L_2\left(s\right)\left|\left(\varphi x\right)\left(s\right)\right|+L_3\left(s\right)\left|\left(\psi x\right)\left(s\right)\right|+M\right)\mathsf{\text{d}}s\right.\\ +\left.\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\left(L_1\left(s\right)\left|x\left(s\right)\right|+L_2\left(s\right)\left|\left(\varphi x\right)\left(s\right)\right|+L_3\left(s\right)\left|\left(\psi x\right)\left(s\right)\right|+M\right)\mathsf{\text{d}}s\right)\\ \le \underset{t\in \left[0,T\right]}{sup}\left(\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\left(L_1\left(s\right)\left|x\left(s\right)\right|+{\gamma }_0{L}_2\left(s\right)\left|x\left(s\right)\right|\right.\right.\\ +\left.{\delta }_0{L}_3\left(s\right)\left|x\left(s\right)\right|+M\right)\mathsf{\text{d}}s\\ +\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\left(L_1\left(s\right)\left|x\left(s\right)\right|+{\gamma }_0{L}_2\left(s\right)\right.\left|x\left(s\right)\right|\\ +\left.\left.{\delta }_0{L}_3\left(s\right)\left|x\left(s\right)\right|+M\right)\mathsf{\text{d}}s\right)\\ \le \underset{t\in \left[0,T\right]}{sup}\left(\left(I^{\alpha }{L}_1\left(t\right)+{\gamma }_0{I}^{\alpha }{L}_2\left(t\right)+{\delta }_0{I}^{\alpha }{L}_3\left(t\right)\right)r+\frac{M{t}^q}{\mathrm{\Gamma }\left(q+1\right)}\right.\\ +\left.\left|{\nu }_1\right|t^{\alpha -1}\left(I^{\left(2\alpha -1\right)}{L}_1\left(\eta \right)+{\gamma }_0{I}^{\left(2\alpha -1\right)}{L}_2\left(\eta \right)+{\delta }_0{I}^{\left(2\alpha -1\right)}{L}_3\left(\eta \right)\right)r+\frac{M{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right)\\ \le \left({\xi }_1+\left|{\nu }_1\right|T^{\alpha -1}{\xi }_2\right)\left(1+{\gamma }_0+{\delta }_0\right)r+M{T}^{\alpha -1}\left(\frac{T}{\mathrm{\Gamma }\left(\alpha +1\right)}+\frac{\left|{\nu }_1\right|{\eta }^{\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right)\\ =\mathrm{\Lambda }r+M\epsilon \le r\end{array}$$

In view of (A₁), for every t ∈ [0, T], we have

$$\begin{array}{c}|\left(\mathcal{P}u\right)\left(t\right)-\left(\mathcal{P}v\right)\left(t\right)|\\ \le {\mathsf{\text{sup}}}_{t\in \left[0,T\right]}\left(\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\right.|f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)-f\left(s,v\left(s\right),\left(\varphi v\right)\left(s\right),\left(\psi v\right)\left(s\right)\right)|\mathsf{\text{d}}s\right.\\ +\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}\left.|f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)-f\left(s,\upsilon \left(s\right),\left(\varphi v\right)\left(s\right),\left(\psi v\right)\left(s\right)\right)|\mathsf{\text{d}}s\right.\right)\\ \le {\mathsf{\text{sup}}}_{t\in \left[0,T\right]}\left(\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}\left(L_1\left(s\right)|u-v|+L_2\left(s\right)\left|\varphi v\right|+L_3\left(s\right)|\psi u-\psi v|\right)\right.\mathsf{\text{d}}s\\ +\left|{\nu }_1\right|t^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -2}}{\mathrm{\Gamma }\left(2\alpha -1\right)}|\left.\left(L_1\left(s\right)|u-v|+L_2\left(s\right)|\varphi u-\varphi v|+L_3\left(s\right)|\psi u-\psi v|\right)\parallel \mathsf{\text{d}}s\right)\\ \le {\mathsf{\text{sup}}}_{t\in \left[0,T\right]}\left(\left(I^{\alpha }{L}_1\left(t\right)+{\gamma }_0{I}^{\alpha }{L}_2\left(t\right)\right.+{\delta }_0{I}^{\alpha }{L}_3\left(t\right)\right)\parallel u-v\parallel \\ +\left|{\nu }_1\right|T^{\alpha -1}\left(I^{\left(2\alpha -1\right)}{L}_1\left(\eta \right)+{\gamma }_0{I}^{\left(2\alpha -1\right)}{L}_2\left(\eta \right)+{\delta }_0{I}^{\left(2\alpha -1\right)}{L}_3\left(\eta \right)\right)\parallel u-v\parallel \\ \le \left({\xi }_1+\left|{\nu }_1\right|T^{\alpha -1}{\xi }_2\right)\left(1+{\gamma }_0+{\delta }_0\right)\parallel u-v\parallel =\mathrm{\Lambda }\parallel u-v\parallel \end{array}$$

By assumption (A₂), Λ < 1, therefore, the operator $\mathcal{P}$ is a contraction. Hence, by Banach fixed point theorem, we deduce that $\mathcal{P}$ has a unique fixed point which in fact is a unique solution of problem (1.1) and (1.2)-(1.3). This completes the proof.   □

Theorem 3.4 (Krasnoselskii's fixed point theorem [22]). Let$\mathcal{M}$be a closed convex and nonempty subset of a Banach space X. Let A, B be the operators such that (i)$Ax+By\in \mathcal{M}$whenever$x,y\in \mathcal{M}$; (ii) A is compact and continuous; (iii) B is a contraction mapping. Then, there exists$z\in \mathcal{M}$such that z = Az + Bz.

Theorem 3.5 Assume that f: [0, T] × ℝ × ℝ × ℝ → ℝ is a continuous function and the following assumptions hold:

(H ₁ )

$$\begin{array}{c}|f\left(t,u\left(t\right),\left(\varphi u\right)\left(t\right),\left(\psi u\right)\left(t\right)\right)-f\left(t,v\left(t\right),\left(\varphi v\right)\left(t\right),\left(\psi v\right)\left(t\right)\right)|\\ \le L_1\left(t\right)|u-v|+L_2\left(t\right)|\varphi u-\varphi v|+L_3\left(t\right)|\psi u-\psi v|,\forall t\in \left[0,T\right],u,v\in ℝ.\end{array}$$

(H ₂ ) |f (t,u)| ≤ μ(t), ∀(t,u)∈[0, T] × ℝ, and μ ∈ C([0, T],ℝ⁺).

If

$$\frac{\left|{\nu }_1\right|T^{\alpha -1}{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}<1,$$

(3.1)

then the boundary value problem (1.1) and (1.2)-(1.3) has at least one solution on [0, T].

Proof Letting sup_{t∈[0, T]}|μ(t)| = ||μ||, we fix

$$\bar{r}\ge \parallel \mu \parallel T^{\alpha -1}\left(\frac{T}{\mathrm{\Gamma }\left(\alpha +1\right)}+\frac{\left|{\nu }_1\right|{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right),$$

and consider $B_{\bar{r}}=\left\{u\in \mathcal{C}:\parallel u\parallel \le \bar{r}\right\}$. We define the operators ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ on $B_{\bar{r}}$ as

$$\begin{array}{c}\left({\mathcal{P}}_{1}u\right)\left(t\right)=\underset{0}{\overset{t}{\int }}\frac{{\left(t-s\right)}^{\alpha -1}}{\mathrm{\Gamma }\left(\alpha \right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s,\\ \left({\mathcal{P}}_{2}u\right)\left(t\right)={\nu }_1{t}^{\alpha -1}\underset{0}{\overset{\eta }{\int }}\frac{{\left(\eta -s\right)}^{2\alpha -s}}{\mathrm{\Gamma }\left(2\alpha -1\right)}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\left(s\right)\right)\mathsf{\text{d}}s\right).\end{array}$$

For $u,v\in B_{\bar{r}}$, we find that

$$\parallel {\mathcal{P}}_{1}u+{\mathcal{P}}_{2}v\parallel \le \parallel \mu \parallel T^{\alpha -1}\left(\frac{T}{\mathrm{\Gamma }\left(\alpha +1\right)}+\frac{\left|{\nu }_1\right|{\eta }^{2\alpha -1}}{\mathrm{\Gamma }\left(2\alpha \right)}\right)\le \bar{r}.$$

Thus, ${\mathcal{P}}_{1}u+{\mathcal{P}}_{2}v\in B_{\bar{r}}$. It follows from the assumption (H₁) together with (3.1) that ${\mathcal{P}}_2$ is a contraction mapping. Continuity of f implies that the operator ${\mathcal{P}}_1$ is continuous.

Also, ${\mathcal{P}}_1$ is uniformly bounded on $B_{\bar{r}}$ as

$$\parallel {\mathcal{P}}_{1}u\parallel \le \frac{\parallel u\parallel T^{\alpha }}{\mathrm{\Gamma }\left(\alpha +1\right)}.$$

Now we prove the compactness of the operator ${\mathcal{P}}_1$.

In view of (H₁), we define ${\mathsf{\text{sup}}}_{\left(t,x,\varphi x,\psi x\right)\in \left[0,T\right]\times B_r\times B_r\times B_r}\left|f\left(t,x,\varphi x,\psi x\right)\right|=\bar{f}$, and consequently we have

$$\begin{array}{c}|\left({\mathcal{P}}_{1}u\right)\left(t_1\right)-\left({\mathcal{P}}_{2}u\right)\left(t_2\right)|\\ =\left|\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}\right.\underset{0}{\overset{t_1}{\int }}\left[{\left(t_1-s\right)}^{\alpha -1}-{\left(t_2-s\right)}^{\alpha -1}\right]\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\\ -\left.\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}\underset{t_1}{\overset{t_2}{\int }}{\left(t_2-s\right)}^{\alpha -1}f\left(s,u\left(s\right),\left(\varphi u\right)\left(s\right),\left(\psi u\right)\left(s\right)\right)\mathsf{\text{d}}s\right|\\ \le \frac{\bar{f}}{\mathrm{\Gamma }\left(\alpha +1\right)}|2{\left(t_2-t_1\right)}^{\alpha }+t_1^{\alpha }-t_2^{\alpha }|,\end{array}$$

which is independent of u and tends to zero as t₂ → t₁. So, ${\mathcal{P}}_1$ is relatively compact on $B_{\bar{r}}$. Hence, by the Arzelá-Ascoli Theorem, ${\mathcal{P}}_1$ is compact on $B_{\bar{r}}$. Thus, all the assumptions of Theorem 3.4 are satisfied. So the conclusion of Theorem 3.4 implies that the boundary value problem (1.1) and (1.2)-(1.3) has at least one solution on [0, T]. This completes the proof.   □