New conditions on the existence and stability of positive periodic solutions for n-species Lotka-Volterra systems with deviating arguments

Abstract

In this paper, we study the existence and stability of positive periodic solutions for an n-species Lotka-Volterra system with deviating arguments, $x_i^{\prime }(t)=x_i(t)(b_i{r}_i(t)-a_{ii}(t)x_i(t-{\tau }_{ii}(t))-{\sum }_{j=1,j\ne i}^n{k}_{ij}{a}_{ij}(t)x_j(t-{\tau }_{ij}(t)))$, $i=1,2,\dots ,n$, referred to as (E). By using Mawhin’s coincidence degree, matrix spectral theory, and some new estimation techniques for the prior bounds of unknown solutions to the equation $Lx=\lambda Nx$, some new and interesting sufficient conditions are obtained guaranteeing the existence and global stability of positive periodic solutions of the above system. The model studied in this paper is more general, and it includes some known Lotka-Volterra type systems, such as competitive systems, predator-prey systems, and competitor-mutualist systems. Our new results are different from the known results in the previous literature.

MSC:34K13, 37B25.

1 Introduction

In recent years, various delay differential equation models have been proposed in the study of population ecology and infectious diseases. One of the most famous models is the Lotka-Volterra system. Because of its theoretical and practical significance, Lotka-Volterra systems have been extensively and intensively studied for the past few years (see, e.g., [1–7]). In particular, Xia and Han [2] investigated the existence and stability of the following periodic n-species Lotka-Volterra competitive system:

$$y_i^{\prime }(t)=y_i(t)(b_i(t)-\sum _{j=1}^n{a}_{ij}(t)y_j(t)),i=1,2,\dots ,n,$$

(1.1)

where $b_i,a_{ij}\in C(\mathbb{R},[0,\mathrm{\infty }))$ are w-periodic functions ($\omega >0$) with $a_{ii}>0$. They obtain one results as follows.

Theorem 1.1 Assume that the following conditions hold:

(A₁) $m(b_i)>{\sum }_{j=1,j\ne i}^{n}m(a_{ij})\frac{m(b_j)}{m(a_{jj})}$, $i=1,2,\dots ,n$;

(A₂) $\rho (K)<1$, where $K={({\mathrm{\Gamma }}_{ij})}_{n\times n}$ and

$${\mathrm{\Gamma }}_{ij}=\{\begin{array}{ll}0,& i=j,\\ {\overline{a}}_{ij}{\underline{a}}_{jj}^{-1},& i\ne j.\end{array}$$

Then system (1.1) has at least one positive ω-periodic solution.

In the proof of Theorem 1.1, the author did not consider the deviating arguments in every terms $a_{ij}(t)x_j(t)$, $i,j=1,2,\dots ,n$. Thus, Theorem 1.1 cannot be applied to system (E) when ${\tau }_{ij}(t)\ne 0$.

Recently, by using the method of Krasnoselskii’s fixed point theorem, Tang and Zou [1] investigated the existence of positive periodic solutions of the following system with deviating arguments:

$$x_i^{\prime }(t)=x_i(t)(r_i(t)-\sum _{j=1}^n{a}_{ij}(t)x_j(t-{\tau }_{ij}(t))),i=1,2,\dots ,n.$$

(1.2)

By the same method of [1], Lv et al. [4] investigated the existence and global attractivity of positive periodic solutions of 3-species Lotka-Volterra predator-prey systems with deviating arguments as follows:

$$\{\begin{array}{l}{x}_1^{\prime }(t)=x_1(t)(r_1(t)-a_{11}(t)x_1(t-{\tau }_{11}(t))\\ \phantom{x_1^{\prime }(t)=}-a_{12}(t)x_2(t-{\tau }_{12}(t))-a_{13}(t)x_3(t-{\tau }_{13}(t))),\\ x_2^{\prime }(t)=x_2(t)(-r_2(t)+a_{21}(t)x_1(t-{\tau }_{21}(t))\\ \phantom{x_2^{\prime }(t)=}-a_{22}(t)x_2(t-{\tau }_{22}(t))-a_{23}(t)x_3(t-{\tau }_{23}(t))),\\ x_3^{\prime }(t)=x_3(t)(-r_3(t)+a_{31}(t)x_1(t-{\tau }_{31}(t))\\ \phantom{x_3^{\prime }(t)=}-a_{32}(t)x_2(t-{\tau }_{32}(t))-a_{33}(t)x_3(t-{\tau }_{33}(t))).\end{array}$$

(1.3)

Compared to system (1.2), the front sign of coefficients of system (1.3) could change.

In this paper, motivating by some ideas in [2], we generalize system (1.3) to a model with n-species,

$$\begin{array}{c}{x}_i^{\prime }(t)=x_i(t)(b_i{r}_i(t)-a_{ii}(t)x_i(t-{\tau }_{ii}(t))-\sum _{j=1,j\ne i}^n{k}_{ij}{a}_{ij}(t)x_j(t-{\tau }_{ij}(t))),\hfill \\ i=1,2,\dots ,n,\hfill \end{array}$$

(1.4)

where $r_i,a_{ij}\in C(\mathbb{R},[0,\mathrm{\infty }))$ and ${\tau }_{ij}\in C^1(\mathbb{R},\mathbb{R})$ are w-periodic functions ($\omega >0$), $b_i=1\text{ or }-1$, $k_{ij}=1\text{ or }-1$, with

$$\begin{array}{c}m(r_i)=\frac{1}{w}{\int }_0^w{r}_i(s)ds>0,m(a_{ij})=\frac{1}{w}{\int }_0^w{a}_{ij}(s)ds\ge 0,\hfill \\ {\tau }_{ij}^{\prime }<1,i,j=1,2,\dots ,n.\hfill \end{array}$$

For the biological point of view, it is always assumed that $a_{ii}$ is strictly positive.

It is not difficult to see that all the above mentioned models are special cases of this model. Thus, it is worth investigating the existence and stability of positive periodic solutions of system (1.4). To the best of our knowledge, very few authors have been concerned with employing matrix spectral theory to obtain the prior bounds for biological systems so far. In this paper, by combing matrix spectral theory with Mawhin’s coincidence degree theory, we manage to obtain a set of new and interesting conditions, which are very different from the known results in the literature.

The structure of this paper is as follows. In Section 2, some new and interesting sufficient conditions for the existence of positive periodic solutions of system (1.4) are obtained. In Section 3, we will explore the stability of positive periodic solution of system (1.4). Finally, an example is given to show that the results of this paper are easily applicable.

2 Existence of positive periodic solutions

In this section, we shall obtain some new sufficient conditions for the existence of a positive periodic solution of system (1.4).

For convenience, we introduce some notations, definitions, and lemmas. Let $\omega >0$ be a constant, denote $C_{\omega }=\{x|x\in C(\mathbb{R},{\mathbb{R}}^n),x(t+\omega )=x(t)\}$, with the norm

$$\parallel x\parallel =\underset{t\in [0,\omega ]}{max}{\left(\sum _{i=1}^n\right|x_i(t){|}^2)}^{\frac{1}{2}}$$

and ${|x_i|}_0={max}_{t\in [0,\omega ]}|x_i(t)|$, $\mathrm{\forall }x\in C_{\omega }$. If $f(t)$ is a continuous ω-periodic function defined on ℝ, denote

$$\underline{f}=\underset{t\in [0,\omega ]}{min}|f(t)|,\overline{f}=\underset{t\in [0,\omega ]}{max}|f(t)|,m(f)=\frac{1}{w}{\int }_0^{w}f(t)dt.$$

For the matrix $G={(g_{ij})}_{n\times n}$, $G^T$ denotes the transpose of G, and $E_n$ denotes the identity matrix of size n. $diag(\cdot )$ represents a diagonal matrix with specified diagonal entries. A matrix or vector $A\ge 0$ means that all entries of A are greater than or equal to zero. $A>0$ can be defined similarly. For matrices or vectors A and B, $A\ge B$ (resp., $A>B$) means that $A-B\ge 0$ (resp., $A-B>0$). We denote the spectral radius of the matrix A by $\rho (A)$.

Lemma 2.1 ([3])

If $\tau \in C_{\omega }$ satisfies $\tau \in C^1(\mathbb{R},\mathbb{R})$ and ${\tau }^{\prime }(t)<1$, $\mathrm{\forall }t\in [0,w]$, then the function $t-\tau (t)$ has a unique inverse function satisfying $\sigma \in C(\mathbb{R},\mathbb{R})$ and $\sigma (t+\omega )=\sigma (t)$, $\mathrm{\forall }t\in \mathbb{R}$.

Remark 2.1 If $g\in C_{\omega }$, $\tau \in C_{\omega }$ and ${\tau }^{\prime }(t)<1$, $\mathrm{\forall }t\in [0,w]$, from Lemma 2.1, we have $g(\sigma (t+\omega ))=g(\sigma (t)+\omega )=g(\sigma (t))$, $\mathrm{\forall }t\in \mathbb{R}$, where $\sigma (t)\in C(\mathbb{R},\mathbb{R})$ is the inverse function of $t-\tau (t)$, thus $g(\sigma (t))\in C_{\omega }$.

Definition 2.1 ([8])

A real $n\times n$ matrix $A=(a_{ij})$ is said to be an M-matrix if $a_{ij}\le 0$, $i,j=1,2,\dots ,n$, $i\ne j$, and $A^{-1}\ge 0$.

Lemma 2.2 ([9])

Let $A\ge 0$ be an $n\times n$ matrix and let $\rho (A)<1$. Then ${(E_n-A)}^{-1}\ge 0$, where $E_n$ denotes the identity matrix of size n.

In order to use Mawhin’s continuation theorem, we recall this theorem first.

Let X, Y be real Banach spaces, let $L:D(L)\subset X\to Y$ be a Fredholm operator with index zero. Here, $D(L)$ denotes the domain of L. This means that ImL is closed in Y and $dimKerL=dim(Y/ImL)<+\mathrm{\infty }$. Consider the supplementary subspaces $X_1$ and $Y_1$ such that $X=KerL\oplus X_1$, $Y=ImL\oplus Y_1$ and let $P:X\to KerL$, $Q:Y\to Y_1$ be the natural projections. Clearly, $KerL\cap (D(L)\cap X_1)=\{0\}$, thus the restriction $L:L{|}_{D(L)\cap X_1}$ is invertible. Denote the inverse of L by $K_P$.

Now, let Ω be an open bounded subset of X with $D(L)\cap \mathrm{\Omega }\ne \mathrm{\varnothing }$, a map $N:\overline{\mathrm{\Omega }}\to Y$ is said to be L-compact on $\overline{\mathrm{\Omega }}$, if $QN(\overline{\mathrm{\Omega }})$ is bounded and the operator $K_P(I-Q)N:\overline{\mathrm{\Omega }}\to Y$ is compact.

Lemma 2.3 (Mawhin [10])

Suppose that X and Y are two Banach spaces, and that $L:D(L)\subset X\to Y$ is a Fredholm operator with index zero. Furthermore, $\mathrm{\Omega }\in X$ is an open bounded set, and $N:\overline{\mathrm{\Omega }}\to Y$ is L-compact on $\overline{\mathrm{\Omega }}$. Assume of the following conditions to hold:

• (i) $Lx\ne \lambda Nx$, $\mathrm{\forall }x\in \partial \mathrm{\Omega }\cap D(L)$, $\lambda \in (0,1)$;

• (ii) $QNx\ne 0$, $\mathrm{\forall }x\in \partial \mathrm{\Omega }\cap KerL$;

• (iii) $deg\{JQN,\mathrm{\Omega }\cap KerL,0\}\ne 0$. Here $J:ImQ\to KerL$ is an isomorphism. Then the equation $Lx=Nx$ has at least one solution on $\overline{\mathrm{\Omega }}\cap D(L)$.

Using Lemma 2.1, we denote the inverse function $t-{\tau }_{ij}(t)$ by ${\sigma }_{ij}(t)$ ($i,j=1,2,\dots ,n$) and let

$$p_{ij}(t):=\frac{a_{ij}({\sigma }_{ij}(t))}{1-{\tau }_{ij}^{\prime }({\sigma }_{ij}(t))},i,j=1,2,\dots ,n.$$

(2.1)

Theorem 2.1 Assume that the following conditions hold:

• (H1) The algebraic equation system

  $$b_{i}m(r_i)-m(a_{ii})e^{y_i}-\sum _{j=1,j\ne i}^n{k}_{ij}m(a_{ij})e^{y_j}=0,i=1,2,\dots ,n,$$

  has a unique solution $(y_1^{\ast },y_2^{\ast },\dots ,y_n^{\ast })\in {\mathbb{R}}^n$;

• (H2) $\rho (K)<1$, where $K={({\mathrm{\Gamma }}_{ij})}_{n\times n}$ and

  $${\mathrm{\Gamma }}_{ij}=\{\begin{array}{ll}0,& i=j,\\ {\overline{p}}_{ij}{\underline{p}}_{jj}^{-1},& i\ne j,\end{array}$$

  where $p_{ij}$, $i,j=1,2,\dots ,n$, is defined by (2.1);

• (H3) ${\underline{r}}_i{\overline{p}}_{ii}^{-1}-{\sum }_{j=1,j\ne i}^n{\overline{p}}_{ij}{\overline{p}}_{ii}^{-1}{\underline{p}}_{jj}^{-1}{\omega }^{-1}{h}_j>0$, $i=1,2,\dots ,n$, where $H={(h_1,h_2,\dots ,h_n)}^T:={(E_n-K)}^{-1}D$, $D={(D_1,D_2,\dots ,D_n)}^T={({\overline{r}}_1\omega ,{\overline{r}}_2\omega ,\dots ,{\overline{r}}_n\omega )}^T$.

Then system (1.4) has at least one positive ω-periodic solution.

Proof Make the change of variables

$$x_i(t)=e^{y_i(t)},i=1,2,\dots ,n.$$

(2.2)

Then system (1.4) can be rewritten as

$$y_i^{\prime }(t)=b_i{r}_i(t)-a_{ii}(t)e^{y_i(t-{\tau }_{ii}(t))}-\sum _{j=1,j\ne i}^n{k}_{ij}{a}_{ij}(t)e^{y_j(t-{\tau }_{ij}(t))},i=1,2,\dots ,n.$$

(2.3)

Obviously, system (1.4) has a positive ω-periodic solution if and only if system (2.3) has a ω-periodic solution.

By Lemma 2.3, we set $X=Y=C_{\omega }$, $D(L)=\{y|y\in X,y(t)\in C_{\omega }^1(\mathbb{R},{\mathbb{R}}^n)\}$, and

$$\begin{array}{c}L:D(L)\cap X\to Y,Ly=\frac{dy(t)}{dt},\hfill \\ N:X\to Y,[Ny](t)={({(Ny)}_1(t),{(Ny)}_2(t),\dots ,{(Ny)}_n(t))}^T,\hfill \end{array}$$

where

$${(Ny)}_i(t)=b_i{r}_i(t)-a_{ii}(t)e^{y_i(t-{\tau }_{ii}(t))}-\sum _{j=1,j\ne i}^n{k}_{ij}{a}_{ij}(t)e^{y_j(t-{\tau }_{ij}(t))},i=1,2,\dots ,n.$$

(2.4)

Obviously, $KerL=R^n$, $ImL=\{y\in Y|{\int }_0^{w}y(t)dt=0\}$. So ImL is closed in $C_{\omega }$ and $dimKerL=codimImL=n$, then the operator L is a Fredholm operator with index zero.

Let the projectors $P:X\to KerL$ and $Q:Y\to ImQ$ be defined by

$$Px=\frac{1}{w}{\int }_0^{w}x(t)dt,Qy=\frac{1}{w}{\int }_0^{w}y(t)dt.$$

Then, P, Q are continuous operators such that $KerL=ImP$, $KerQ=ImL$. Furthermore, the generalized inverse $K_P:ImL\to D(L)\cap KerP$ exists, which is given by

$$K_P(y)={\int }_0^{t}y(s)ds-\frac{1}{w}{\int }_0^w{\int }_0^{t}y(s)dsdt.$$

(2.5)

Assume that $y(t)$ is an arbitrary solution of the equation $Ly=\lambda Ny$ for each $\lambda \in (0,1)$, that is,

$$y_i^{\prime }(t)=\lambda (b_i{r}_i(t)-a_{ii}(t)e^{y_i(t-{\tau }_{ii}(t))}-\sum _{j=1,j\ne i}^n{k}_{ij}{a}_{ij}(t)e^{y_j(t-{\tau }_{ij}(t))}),i=1,2,\dots ,n.$$

Integrating it on the interval $[0,\omega ]$ gives

$${\int }_0^w{a}_{ii}(s)e^{y_i(s-{\tau }_{ii}(s))}ds={\int }_0^w{b}_i{r}_i(s)ds-{\int }_0^w\sum _{j=1,j\ne i}^n{k}_{ij}{a}_{ij}(s)e^{y_j(s-{\tau }_{ij}(s))}ds,$$

(2.6)

and by using Lemma 2.1, Remark 2.1, and (2.1), we see

$${\int }_0^w{p}_{ii}(s)e^{y_i(s)}ds={\int }_0^w{b}_i{r}_i(s)ds-{\int }_0^w\sum _{j=1,j\ne i}^n{k}_{ij}{p}_{ij}(s)e^{y_j(s)}ds,$$

it follows that

$${\underline{p}}_{ii}{\int }_0^w{e}^{y_i(s)}ds\le {\overline{r}}_i\omega +\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\int }_0^w{e}^{y_j(s)}ds.$$

(2.7)

Letting ${\underline{p}}_{ii}{\int }_0^w{e}^{y_i(s)}ds=z_i$, it follows from (2.7) that

$$z_i\le {\overline{r}}_i\omega +\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\underline{p}}_{jj}^{-1}{z}_j$$

or

$$z_i-\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\underline{p}}_{jj}^{-1}{z}_j\le {\overline{r}}_i\omega ,$$

(2.8)

which implies

$$\left(\begin{array}{cccc}1& -{\underline{p}}_{22}^{-1}{\overline{p}}_{12}& \cdots & -{\underline{p}}_{nn}^{-1}{\overline{p}}_{1n}\\ -{\underline{p}}_{11}^{-1}{\overline{p}}_{21}& 1& \cdots & -{\underline{p}}_{nn}^{-1}{\overline{p}}_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ -{\underline{p}}_{11}^{-1}{\overline{p}}_{n1}& -{\underline{p}}_{22}^{-1}{\overline{p}}_{n2}& \cdots & 1\end{array}\right)\left(\begin{array}{c}{z}_1\\ z_2\\ \cdots \\ z_n\end{array}\right)\le \left(\begin{array}{c}{\overline{r}}_1\omega \\ {\overline{r}}_2\omega \\ \cdots \\ {\overline{r}}_n\omega \end{array}\right).$$

(2.9)

It follows from (2.9) that

$$(E_n-K){(z_1,z_2,\dots ,z_n)}^T\le D.$$

(2.10)

In view of $\rho (K)<1$ and Lemma 2.2, we have ${(E_n-K)}^{-1}\ge 0$. That is,

$$H={(h_1,h_2,\dots ,h_n)}^T:={(E_n-K)}^{-1}D\ge 0.$$

(2.11)

Then it follows from (2.10) and (2.11) that

$${(z_1,z_2,\dots ,z_n)}^T\le H\text{or}{z}_i\le h_i,i=1,2,\dots ,n,$$

(2.12)

which implies that there exists a ${\xi }_i\in [0,\omega ]$, such that $e^{y_i({\xi }_i)}\le \frac{h_i}{{\underline{p}}_{ii}\omega }$, $i=1,2,\dots ,n$, i.e.,

$$y_i({\xi }_i)\le ln\frac{h_i}{{\underline{p}}_{ii}\omega },i=1,2,\dots ,n.$$

(2.13)

By (2.6), we have

$$|{\int }_0^w{p}_{ii}(s)e^{y_i(s)}ds|=|{\int }_0^w{b}_i{r}_i(s)ds-{\int }_0^w\sum _{j=1,j\ne i}^n{k}_{ij}{p}_{ij}(s)e^{y_j(s)}ds|,$$

i.e.,

$${\overline{p}}_{ii}{\int }_0^w{e}^{y_i(s)}ds\ge {\int }_0^w{r}_i(s)ds-\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\int }_0^w{e}^{y_j(s)}ds$$

or

$${\overline{p}}_{ii}{\int }_0^w{e}^{y_i(s)}ds\ge {\underline{r}}_i\omega -\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\underline{p}}_{jj}^{-1}{h}_j,$$

which implies there exists a ${\eta }_i\in [0,w]$, such that

$$e^{y_i({\eta }_i)}\ge {\underline{r}}_i{\overline{p}}_{ii}^{-1}-\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\overline{p}}_{ii}^{-1}{\underline{p}}_{jj}^{-1}{\omega }^{-1}{h}_j,$$

and from the condition (H3), we have

$$y_i({\eta }_i)\ge ln({\underline{r}}_i{\overline{p}}_{ii}^{-1}-\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\overline{p}}_{ii}^{-1}{\underline{p}}_{jj}^{-1}{\omega }^{-1}{h}_j),$$

using (2.13) and combining the continuous function intermediate value theorem, there exists a ${\zeta }_i\in [0,\omega ]$, such that

$$|y_i({\zeta }_i)|\le max\left\{\right|ln\frac{h_i}{{\underline{p}}_{ii}\omega }|,|ln({\underline{r}}_i{\overline{p}}_{ii}^{-1}-\sum _{j=1,j\ne i}^n{\overline{p}}_{ij}{\overline{p}}_{ii}^{-1}{\underline{p}}_{jj}^{-1}{\omega }^{-1}{h}_j)\left|\right\}:=M_i,i=1,2,\dots ,n,$$

i.e.,

$${|y_i|}_0\le M_i+{\int }_0^w|y_i^{\prime }(s)|ds,i=1,2,\dots ,n.$$

(2.14)

On the other hand,

$$\begin{array}{rcl}{\int }_0^w|y_i^{\prime }(s)|ds& \le & {\int }_0^w{r}_i(s)ds+{\int }_0^w\sum _{j=1}^n{p}_{ij}(s)e^{y_j(s)}ds\\ \le & {\overline{r}}_i\omega +\sum _{j=1}^n{\overline{p}}_{ij}{\int }_0^w{e}^{y_j(s)}ds\\ \le & {\overline{r}}_i\omega +\sum _{j=1}^n{\overline{p}}_{ij}{\underline{p}}_{jj}^{-1}{h}_j\\ :=& R_i.\end{array}$$

Combining with (2.14), we have

$${|y_i|}_0\le M_i+R_i,i=1,2,\dots ,n,$$

furthermore, we have

$$\parallel y\parallel =\underset{t\in [0,\omega ]}{max}{\left(\sum _{j=1}^n\right|y_i(t){|}^2)}^{\frac{1}{2}}\le {\left(\sum _{j=1}^n{(M_i+R_i)}^2\right)}^{\frac{1}{2}}:=M.$$

Clearly, $M<+\mathrm{\infty }$ is a constant independent of λ.

If $y\in KerL$, then $y\in {\mathbb{R}}^n$ is a constant vector, thus

$$QN{y}_i=b_{i}m(r_i)-m(a_{ii})e^{y_i}-\sum _{j=1,j\ne i}^n{k}_{ij}m(a_{ij})e^{y_j},i=1,2,\dots ,n.$$

If $QNy=0$, then

$$m(a_{ii})e^{y_i}-\sum _{j=1,j\ne i}^n{k}_{ij}m(a_{ij})e^{y_j}=b_{i}m(r_i).$$

It follows from (H1) that the algebraic equation has a unique solution $y^{\ast }=(y_1^{\ast },y_2^{\ast },\dots ,y_n^{\ast })$. Let $G:={|y^{\ast }|}_0={({\sum }_{j=1}^n{(y_i^{\ast })}^2)}^{\frac{1}{2}}$. Then $G<+\mathrm{\infty }$ is a constant.

Set $\mathrm{\Omega }=\{y={(y_1,y_2,\dots ,y_n)}^T\in X,\parallel y\parallel <M+G\}$. Obviously, conditions (i) and (ii) in Lemma 2.3 are satisfied. Moreover, it is easy to see that

$$deg\{JQN,\mathrm{\Omega }\cap KerL,0\}=sign\{{(-1)}^{n}det[l_{ij}m(a_{ij})]e^{{\sum }_{j=1}^n{y}_j^{\ast }}\}\ne 0,$$

where

$$l_{ij}=\{\begin{array}{ll}1,& i=j,\\ k_{ij},& i\ne j.\end{array}$$

J is an identity mapping. Therefore, by using Lemma 2.3, we find that system (2.3) has at least one ω-periodic solution. By (2.2), system (1.4) has at least one positive ω-periodic solution. This completes the proof of Theorem 2.1. □

3 Global asymptotic stability of positive periodic solutions

Under the assumption of Theorem 2.1, we know that system (1.4) has at least one positive ω-periodic solution, denoted by $x^{\ast }=(x_1^{\ast },x_2^{\ast },\dots ,x_n^{\ast })$. In this section, we always assume the existence of positive periodic solutions and we study the global stability of positive periodic solutions of (1.4).

We recall some facts which will be used in the proof.

Definition 3.1 Let $x^{\ast }(t)={(x_1^{\ast }(t),x_2^{\ast }(t),\dots ,x_n^{\ast }(t))}^T$ be the ω-periodic solution of (1.4) and let $x(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T$ be any positive solution of (1.4); we say that $x^{\ast }(t)$ is globally asymptotically stable if the following conditions hold:

• (i) $x^{\ast }(t)$ is Lyapunov stable;

• (ii) $x^{\ast }(t)$ is globally attractive in the sense that ${lim}_{t\to +\mathrm{\infty }}[x_i(t)-x_i^{\ast }(t)]=0$ for all $i=1,2,\dots ,n$.

Lemma 3.1 ([7])

Let f be a nonnegative function defined on $[0,+\mathrm{\infty })$ such that f is integrable on $[0,+\mathrm{\infty })$ and is uniformly continuous on $[0,+\mathrm{\infty })$. Then ${lim}_{t\to +\mathrm{\infty }}f(t)=0$.

Theorem 3.1 In addition to the existence of positive periodic solutions, assume that ${\tau }_{ii}(t)\equiv 0$, ${\dot{\tau }}_{ij}(t)<1$, $i,j=1,2,\dots ,n$, and that there exist ${\nu }_i>0$, $i=1,2,\dots ,n$, such that

$${\nu }_i{a}_{ii}(t)>\sum _{j=1,j\ne i}^n\frac{{\nu }_j{a}_{ij}({\sigma }_{ij}(t))}{1-{\dot{\tau }}_{ij}({\sigma }_{ij}(t))},i=1,2,\dots ,n,$$

(3.1)

where ${\sigma }_{ij}(t)$ is the inverse function of $t-{\tau }_{ij}(t)$, $i,j=1,2,\dots ,n$. Then system (1.4) has a unique positive ω-periodic solution $x^{\ast }(t)={(x_1^{\ast }(t),x_2^{\ast }(t),\dots ,x_n^{\ast }(t))}^T$ which is globally asymptotically stable.

Proof Set

$${\theta }_i=\underset{t\in [0,w]}{max}\left\{\frac{1}{{\nu }_i{a}_{ii}(t)}\sum _{j=1,j\ne i}^n\frac{{\nu }_j{a}_{ij}({\sigma }_{ij}(t))}{1-{\dot{\tau }}_{ij}({\sigma }_{ij}(t))}\right\},i=1,2,\dots ,n.$$

From (3.1), we have $0\le {\theta }_i<1$, $i=1,2,\dots ,n$, and

$${\theta }_i{\nu }_i{a}_{ii}(t)\ge \sum _{j=1,j\ne i}^n\frac{{\nu }_j{a}_{ij}({\sigma }_{ij}(t))}{1-{\dot{\tau }}_{ij}({\sigma }_{ij}(t))},i=1,2,\dots ,n.$$

(3.2)

Let $x(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T$ be any positive solution of system (1.4). We define a Lyapunov function $V(t)$ as follows:

$$V(t)=\sum _{i=1}^n{\nu }_i\left[\right|ln\left(\frac{x_i(t)}{x_i^{\ast }(t)}\right)|+\sum _{j=1,j\ne i}^n{\int }_{t-{\tau }_{ij}(t)}^t\frac{a_{ij}({\sigma }_{ij}(s))}{1-{\dot{\tau }}_{ij}({\sigma }_{ij}(s))}|x_j(s)-x_j^{\ast }(s)\left|ds\right],t\ge 0.$$

(3.3)

Let $z_i(t)=|x_i(t)-x_i^{\ast }(t)|$. Calculating the upper right derivative of $V(t)$ at time t, it follows from (3.2) and (3.3) that

$$\begin{array}{rcl}{D}^{+}V(t)& \le & \sum _{i=1}^n{\nu }_i(-a_{ii}(t)|x_i(t)-x_i^{\ast }(t)|+\sum _{j=1,j\ne i}^n\frac{a_{ij}({\sigma }_{ij}(t))}{1-{\dot{\tau }}_{ij}({\sigma }_{ij}(t))}|x_j(t)-x_j^{\ast }(t)\left|\right)\\ =& \sum _{i=1}^n(-{\nu }_i{a}_{ii}(t)+\sum _{j=1,j\ne i}^n\frac{{\nu }_j{a}_{ij}({\sigma }_{ij}(t))}{1-{\dot{\tau }}_{ij}({\sigma }_{ij}(t))})|x_i(t)-x_i^{\ast }(t)|\\ \le & -\sum _{i=1}^n{\nu }_i(1-{\theta }_i)a_{ii}(t)|x_i(t)-x_i^{\ast }(t)|\\ \le & -c\sum _{i=1}^n{z}_i(t)\le 0,t\ge 0,\end{array}$$

(3.4)

where $c={max}_{1\le i\le n}{sup}_{t\in [0,\omega ]}\{{\nu }_i(1-{\theta }_i)a_{ii}(t)\}>0$. It follows from (3.4) that $D^{+}V(t)\le 0$. Obviously, the zero solution of (1.4) is Lyapunov stable. On the other hand, let $t_0$ represent the initial time of system (1.4); t is an arbitrary time and $t>t_0$. Then, integrating (3.4) over $[t_0,t]$ leads to

$$V(t)-V(t_0)\le -c{\int }_{t_0}^t\sum _{i=1}^n{z}_i(s)ds,t\ge 0$$

or

$$V(t)+c{\int }_{t_0}^t\sum _{i=1}^n|x_i(t)-x_i^{\ast }(t)|ds\le V(t_0)<+\mathrm{\infty },t\ge t_0.$$

Noting that $V(t)\ge 0$, it follows that

$${\int }_{t_0}^t\sum _{i=1}^n|x_i(t)-x_i^{\ast }(t)|ds\le \frac{V(t_0)}{c}<+\mathrm{\infty },t\ge t_0.$$

Therefore, by Lemma 3.1, we have

$$\underset{t\to +\mathrm{\infty }}{lim}|x_i(t)-x_i^{\ast }(t)|=0,i=1,2,\dots ,n.$$

From Definition 3.1, Theorem 3.1 follows. □

As an application, we consider the following example.

Example 3.1 Considering the following system:

$$\{\begin{array}{l}{x}_1^{\prime }(t)=x_1(t)(2-(1+\frac{1}{2}sint)x_1(t-\frac{1}{2}cost)+\frac{1}{3}(1-\frac{1}{2}cost)x_2(t-\frac{1}{2}sint)),\\ x_2^{\prime }(t)=x_2(t)(1+\frac{1}{4}(1-\frac{1}{3}cost)x_1(t-\frac{1}{3}sint)-\frac{1}{2}(1+\frac{1}{3}sint)x_2(t-\frac{1}{3}cost)).\end{array}$$

(3.5)

Corresponding to system (1.4), we have $n=2$, $\omega =2\pi$, $r_1=2$, $r_2=1$,

$$\begin{array}{c}{p}_{11}(t)=\frac{1+\frac{1}{2}sin({\mu }_{11}(t))}{1+\frac{1}{2}sin({\mu }_{11}(t))}=1,p_{12}(t)=\frac{\frac{1}{3}(1-\frac{1}{2}cos({\mu }_{12}(t)))}{1-\frac{1}{2}cos({\mu }_{12}(t))}=\frac{1}{3},\hfill \\ p_{21}(t)=\frac{\frac{1}{4}(1-\frac{1}{3}cos({\mu }_{21}(t)))}{1-\frac{1}{3}cos({\mu }_{21}(t))}=\frac{1}{4},p_{22}(t)=\frac{\frac{1}{2}(1+\frac{1}{3}sin({\mu }_{22}(t)))}{1+\frac{1}{3}sin({\mu }_{22}(t))}=\frac{1}{2},\hfill \end{array}$$

where ${\mu }_{11}(t)$, ${\mu }_{12}(t)$, ${\mu }_{21}(t)$, ${\mu }_{22}(t)$ are the inverse of $t-\frac{1}{2}cost$, $t-\frac{1}{2}sint$, $t-\frac{1}{3}sint$, $t-\frac{1}{3}cost$, respectively. Then

$$\begin{array}{c}K=\left(\begin{array}{cc}0& \frac{1}{2}\times \frac{1}{3}\\ 1\times \frac{1}{4}& 0\end{array}\right),\hfill \\ \rho (K)=\frac{\sqrt{6}}{12}<1,\hfill \\ {\underline{r}}_1{\overline{p}}_{11}^{-1}-{\overline{p}}_{12}{\overline{p}}_{11}^{-1}{\underline{p}}_{22}^{-1}{\omega }^{-1}{h}_2=\frac{22}{23}>0,\hfill \\ {\underline{r}}_2{\overline{p}}_{22}^{-1}-{\overline{p}}_{21}{\overline{p}}_{22}^{-1}{\underline{p}}_{11}^{-1}{\omega }^{-1}{h}_1=\frac{20}{23}>0,\hfill \end{array}$$

and the algebraic system

$$\{\begin{array}{l}{e}^{y_1}-\frac{1}{3}{e}^{y_2}=2,\\ -\frac{1}{4}{e}^{y_1}+\frac{1}{2}{e}^{y_2}=1\end{array}$$

has a unique solution $y=(y_1,y_2)=(ln\frac{16}{5},ln\frac{18}{5})$. Then (H1)-(H3) of Theorem 2.1 are satisfied. Moreover, if we let $v_1=1$, $v_2=1$, we have

$$\begin{array}{c}{v}_1(1+\frac{1}{2}sint)>\frac{v_2\frac{1}{3}(1-\frac{1}{2}cos({\sigma }_{12}(t)))}{1-\frac{1}{2}cos({\sigma }_{12}(t))},\hfill \\ \frac{v_2}{2}(1+\frac{1}{3}sint)>\frac{v_1\frac{1}{4}(1-\frac{1}{3}cos({\sigma }_{21}(t)))}{1-\frac{1}{3}cos({\sigma }_{21}(t))}.\hfill \end{array}$$

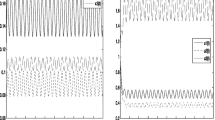
So the conditions of Theorem 3.1 are satisfied. Therefore, system (3.5) has a unique positive 2π-periodic solution which is globally asymptotically stable. In order to see these dynamic properties clearly, we draw the figures for the evolution of the solutions of system (3.5) by using the function ddesd in Matlab; see Figure 1.

Figure 1

The phase portrait and time series of system ( 3.5 ). (a) The 2π-period solution of system (3.5) in the $(x_1,x_2)$ plane. (b), (c) Time series of $x_1$ in $(t,x_1)$ plane. (d), (e) Time series of $x_2$ in the $(t,x_2)$ plane.

Remark 3.1 In view of $k_{12}=k_{21}=-1$ and

$$\begin{array}{c}{\tau }_{11}(t)=\frac{1}{2}cost,{\tau }_{12}(t)=\frac{1}{2}sint,\hfill \\ {\tau }_{21}(t)=\frac{1}{3}sint,{\tau }_{22}(t)=\frac{1}{3}cost,\hfill \end{array}$$

we know that $k_{12}<0$, $k_{21}<0$, ${\tau }_{11}(t)\ne 0$, ${\tau }_{12}(t)\ne 0$, ${\tau }_{21}(t)\ne 0$, ${\tau }_{22}(t)\ne 0$. So the result of the above example cannot be obtained by [2], which implies that the results of this paper are essentially new.