Hyperchaos synchronization of memristor oscillator system via combination scheme

Abstract

In this paper, a hyperchaotic memristor oscillator system is introduced. A new type of synchronization design is proposed to achieve combination synchronization among three different memristor oscillator systems. This all-new control technique can be applied to the general nonlinear systems. The theoretical analysis is verified with numerical simulations showing excellent agreement.

1 Introduction

In recent years, lots of memristor oscillator systems have been used with the purpose of generating signals which are found in radio, satellite communications, switching power supply, etc. [1–10]. By using a passive two-terminal memristor, the memristor oscillator can be fully implemented on-chip with some simple circuit elements. Memristor oscillator systems are good to be used for developing memristive devices and memristive computing. The non-volatile memory of memristor oscillator system has tremendous potential in the dynamic memory and neural synapses [4]. Furthermore, the property can provide us with new methods for high performance computing. Along with the widening of memristor applications, it is necessary to do some deep and detailed research on the related nonlinear dynamics [11–13]. Nonlinear dynamics of memristor oscillator systems is extraordinarily complex [1–4, 6, 8, 10]. Chaotic behavior, sequence of period-doubling bifurcations, inverse sequence of chaotic band, and intermittent chaos are found in various memristor oscillator systems [1–4, 6, 8]. It should be emphasized that hyperchaos with more than one positive Lyapunov exponents has always been a research focus in the fields of lasers, nonlinear oscillators, nonlinear control, secure communication, and so on. Can we design a hyperchaotic memristor oscillator system and investigate its hyperchaotic dynamics? Apparently, this problem is not only of theoretical issue but also a problem of tech-economy as regards electronic circuits. At present, there is little literature on this topic. Based on this consideration, this paper will make a contribution in the context of hyperchaotic memristor oscillator system. In this paper, a fourth-order hyperchaotic memristor oscillator system is systematically illustrated.

Chaotic behavior may be unpredictable, uncoordinated, and constantly shifting under many circumstances. Because of this, chaotic dynamics, synchronization of coupled dynamic systems, and secure communications are always some hot research fields [11, 14–47]. Thus, chaotic systems and the related chaos synchronization problems are important and challenging. By considering linear or nonlinear observers and designing suitable synchronizing signals, a mass of synchronization schemes are developed, such as complete synchronization [11, 14–18], anti-synchronization [19–24], phase synchronization [16, 25–27], lag synchronization [17, 28–36], projective synchronization [17, 37–45], combination synchronization [46, 47]. In the conventional drive-response synchronization schemes, there is just one drive system and one response system. This type of synchronization scheme can be viewed as one-to-one system design and implementation. One-to-one system design and implementation would seem singularly unsuited in many fields of engineering application. In reality, the transmitted signals in secure communication via one-to-one system design and implementation are less vulnerable to malicious attacks and decoding. In many cases, we need to split the transmitted signals into several parts, and then different drive systems load different parts. Therefore, a natural and interesting question is whether we can design some novel synchronization schemes between multi-drive systems and one response system, or between multi-drive systems and multi-response systems? And no matter what the theories say, or what the actual engineering aspects are, these questions are definitely worth exploring. For this reason, based on the combination synchronization in [46, 47], our other objective in this paper is to study the hyperchaos synchronization between two drive memristor oscillator systems and one response memristor oscillator system. The analysis framework and theoretical results in this paper may play an important role in designing memristor oscillatory circuits, sensitive control systems, and signal generation, etc.

Motivated by the above discussions, in this paper, we first introduce and study a hyperchaotic memristor oscillator system. Then we propose a new type of hyperchaos combination synchronization scheme based on two drive systems and one response system. The generalization of synchronization scheme will provide a wider scope for engineering designs and applications. Finally, numerical simulations demonstrate the effectiveness and feasibility of the proposed control scheme. The proposed method in this paper can be applied to the general nonlinear systems.

2 Preliminaries

In this paper, consider a fourth-order memristor oscillator system with its dynamics described by the following equations:

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_1{R}_1}{v}_2(t)-\frac{1}{C_1{R}_1}{v}_1(t)+\frac{G}{C_1}{v}_1(t)-\frac{1}{C_1}W(\phi (t))v_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_2{R}_1}{v}_1(t)-\frac{1}{C_2{R}_1}{v}_2(t)+\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=-\frac{1}{L}{v}_2(t)-\frac{R_2}{L}\ell (t),\end{array}$$

(1)

where $v_1(t)$ and $v_2(t)$ denote voltages, $C_1$ and $C_2$ represent capacitors, $W(\phi (t))$ is memductance function, $R_1$ and $R_2$ are resistors, $\phi (t)$, $\ell (t)$, L and G are magnetic flux, current, inductor and conductance, respectively.

Using the mathematical model of a cubic memristor [1, 2, 8], the memductance function is given by

$$W(\phi (t))=a+3b\phi {(t)}^2,$$

(2)

where a and b are parameters.

From (1) and (2), it follows that

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_1{R}_1}{v}_2(t)-\frac{1}{C_1{R}_1}{v}_1(t)+\frac{G}{C_1}{v}_1(t)-\frac{a}{C_1}{v}_1(t)-\frac{3b}{C_1}\phi {(t)}^2{v}_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_2{R}_1}{v}_1(t)-\frac{1}{C_2{R}_1}{v}_2(t)+\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=-\frac{1}{L}{v}_2(t)-\frac{R_2}{L}\ell (t).\end{array}$$

(3)

By merging similar items,

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_1{R}_1}{v}_2(t)-[\frac{1}{C_1{R}_1}-\frac{G}{C_1}+\frac{a}{C_1}]v_1(t)-\frac{3b}{C_1}\phi {(t)}^2{v}_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_2{R}_1}{v}_1(t)-\frac{1}{C_2{R}_1}{v}_2(t)+\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=-\frac{1}{L}{v}_2(t)-\frac{R_2}{L}\ell (t).\end{array}$$

(4)

Let $x_{11}(t)=\phi (t)$, $x_{12}(t)=v_1(t)$, $x_{13}(t)=v_2(t)$, $x_{14}(t)=\ell (t)$, ${\alpha }_1=\frac{1}{C_1{R}_1}$, ${\alpha }_2=\frac{1}{C_1{R}_1}-\frac{G}{C_1}+\frac{a}{C_1}$, ${\alpha }_3=\frac{3b}{C_1}$, ${\alpha }_4=\frac{1}{C_2{R}_1}$, ${\alpha }_5=\frac{1}{C_2}$, ${\alpha }_6=\frac{1}{L}$, ${\alpha }_7=\frac{R_2}{L}$, then (4) can be rewritten as

$$\{\begin{array}{l}{\dot{x}}_{11}=x_{12},\\ {\dot{x}}_{12}={\alpha }_1{x}_{13}-{\alpha }_2{x}_{12}-{\alpha }_3{x}_{11}^2{x}_{12},\\ {\dot{x}}_{13}={\alpha }_4{x}_{12}-{\alpha }_4{x}_{13}+{\alpha }_5{x}_{14},\\ {\dot{x}}_{14}=-{\alpha }_6{x}_{13}-{\alpha }_7{x}_{14}.\end{array}$$

(5)

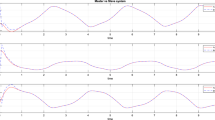
Choose parameters ${\alpha }_1=16.4$, ${\alpha }_2=-3.28$, ${\alpha }_3=19.68$, ${\alpha }_4=1$, ${\alpha }_5=1$, ${\alpha }_6=15$, ${\alpha }_7=0.5$, the initial state $x_{11}(0)=0.01$, $x_{12}(0)=0.01$, $x_{13}(0)=0.01$, $x_{14}(0)=0.01$, by means of a computer program with MATLAB, the corresponding Lyapunov exponents of system (5) are 0.350741, 0.013755, −0.008567, −7.812913. The numerical result is shown in Figure 1, where the first two Lyapunov exponents are positive. Clearly, it implies that memristor oscillator system (5) is hyperchaotic. Figures 2-5 describe the hyperchaotic attractors.

Figure 1

Dynamics of Lyapunov exponents from the fourth-order memristor oscillator system.

Figure 2

3D Projection of the hyperchaotic attractor from the fourth-order memristor oscillator system, ${\mathit{x}}_{\mathbf{11}}$ vs. ${\mathit{x}}_{\mathbf{12}}$ vs. ${\mathit{x}}_{\mathbf{13}}$ .

Figure 3

3D Projection of the hyperchaotic attractor from the fourth-order memristor oscillator system, ${\mathit{x}}_{\mathbf{11}}$ vs. ${\mathit{x}}_{\mathbf{12}}$ vs. ${\mathit{x}}_{\mathbf{14}}$ .

Figure 4

3D Projection of the hyperchaotic attractor from the fourth-order memristor oscillator system, ${\mathit{x}}_{\mathbf{11}}$ vs. ${\mathit{x}}_{\mathbf{13}}$ vs. ${\mathit{x}}_{\mathbf{14}}$ .

Figure 5

3D Projection of the hyperchaotic attractor from the fourth-order memristor oscillator system, ${\mathit{x}}_{\mathbf{12}}$ vs. ${\mathit{x}}_{\mathbf{13}}$ vs. ${\mathit{x}}_{\mathbf{14}}$ .

Remark 1 Although various chaotic memristor oscillator systems have been analyzed extensively in recent years, the hyperchaotic memristor oscillator system is rarely reported and investigated directly. However, the memristor oscillator system (5) achieves hyperchaotic characteristics. Thus, hyperchaotic memristor oscillator system (5) is important for our understanding of the hyperchaotic memristive system.

Now we introduce the scheme of combination synchronization that is needed later.

Consider the first drive system

$${\dot{\chi }}_1=f_1({\chi }_1).$$

(6)

The second drive system is given by

$${\dot{\chi }}_2=f_2({\chi }_2),$$

(7)

and the response system is described by

$${\dot{\chi }}_3=f_3({\chi }_3)+u({\chi }_1,{\chi }_2,{\chi }_3),$$

(8)

where state vectors ${\chi }_1={({\chi }_{11},{\chi }_{12},\dots ,{\chi }_{1n})}^T$, ${\chi }_2={({\chi }_{21},{\chi }_{22},\dots ,{\chi }_{2n})}^T$, ${\chi }_3={({\chi }_{31},{\chi }_{32},\dots ,{\chi }_{3n})}^T$, vector functions $f_1(\cdot ),f_2(\cdot ),f_3(\cdot ):{\mathrm{\Re }}^n\to {\mathrm{\Re }}^n$, $u({\chi }_1,{\chi }_2,{\chi }_3)={(u_1,u_2,\dots ,u_n)}^T:{\mathrm{\Re }}^n\times {\mathrm{\Re }}^n\times \cdots \times {\mathrm{\Re }}^n\to {\mathrm{\Re }}^n$ is the appropriate control input that will be designed in order to obtain a certain control objective.

Definition 1 The drive systems (6), (7), and the response system (8) are said to be combination synchronization if there exist n-dimensional constant diagonal matrices $A_1$, $A_2$, and $A_3\ne 0$ such that

$$\underset{t\to +\mathrm{\infty }}{lim}\parallel e\parallel =\underset{t\to +\mathrm{\infty }}{lim}\parallel A_1{X}_1+A_2{X}_2-A_3{X}_3\parallel =0,$$

(9)

where $\parallel \cdot \parallel$ is vector norm, $e={(e_1,e_2,\dots ,e_n)}^T$ is the synchronization error vector, $X_1=diag({\chi }_{11},{\chi }_{12},\dots ,{\chi }_{1n})$, $X_2=diag({\chi }_{21},{\chi }_{22},\dots ,{\chi }_{2n})$, $X_3=diag({\chi }_{31},{\chi }_{32},\dots ,{\chi }_{3n})$.

Remark 2 In Definition 1, matrices $A_1$, $A_2$, and $A_3$ are often called the scaling matrices. The scheme of combination synchronization is an improvement and extension of the existing synchronization schemes in the literature. When the scaling matrices $A_1=0$ or $A_2=0$, the combination synchronization will degrade into complete synchronization. When the scaling matrices $A_1=A_2=0$, the combination synchronization will change into chaos control.

3 Synchronization criteria

In this paper, consider system (5) as the first drive system and the second drive system is given by

$$\{\begin{array}{l}{\dot{x}}_{21}=x_{22},\\ {\dot{x}}_{22}={\beta }_1{x}_{23}-{\beta }_2{x}_{22}-{\beta }_3{x}_{21}^2{x}_{22},\\ {\dot{x}}_{23}={\beta }_4{x}_{22}-{\beta }_4{x}_{23}+{\beta }_5{x}_{24},\\ {\dot{x}}_{24}=-{\beta }_6{x}_{23}-{\beta }_7{x}_{24},\end{array}$$

(10)

the response system is described by

$$\{\begin{array}{l}{\dot{x}}_{31}=x_{32}+u_1,\\ {\dot{x}}_{32}={\gamma }_1{x}_{33}-{\gamma }_2{x}_{32}-{\gamma }_3{x}_{31}^2{x}_{32}+u_2,\\ {\dot{x}}_{33}={\gamma }_4{x}_{32}-{\gamma }_4{x}_{33}+{\gamma }_5{x}_{34}+u_3,\\ {\dot{x}}_{34}=-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34}+u_4,\end{array}$$

(11)

where ${\beta }_1$, ${\beta }_2$, ${\beta }_3$, ${\beta }_4$, ${\beta }_5$, ${\beta }_6$, ${\beta }_7$, ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, ${\gamma }_4$, ${\gamma }_5$, ${\gamma }_6$, and ${\gamma }_7$ are parameters, $u_1$, $u_2$, $u_3$, $u_4$ are the appropriate control inputs that will be designed.

In our combination synchronization scheme, let $A_1=diag(a_{11},a_{12},a_{13},a_{14})$, $A_2=diag(a_{21},a_{22},a_{23},a_{24})$, $A_3=diag(a_{31},a_{32},a_{33},a_{34})$, thus

$$\{\begin{array}{l}{e}_1=a_{11}{x}_{11}+a_{21}{x}_{21}-a_{31}{x}_{31},\\ e_2=a_{12}{x}_{12}+a_{22}{x}_{22}-a_{32}{x}_{32},\\ e_3=a_{13}{x}_{13}+a_{23}{x}_{23}-a_{33}{x}_{33},\\ e_4=a_{14}{x}_{14}+a_{24}{x}_{24}-a_{34}{x}_{34}.\end{array}$$

(12)

Obviously, we have

$$\{\begin{array}{l}{\dot{e}}_1=a_{11}{\dot{x}}_{11}+a_{21}{\dot{x}}_{21}-a_{31}{\dot{x}}_{31},\\ {\dot{e}}_2=a_{12}{\dot{x}}_{12}+a_{22}{\dot{x}}_{22}-a_{32}{\dot{x}}_{32},\\ {\dot{e}}_3=a_{13}{\dot{x}}_{13}+a_{23}{\dot{x}}_{23}-a_{33}{\dot{x}}_{33},\\ {\dot{e}}_4=a_{14}{\dot{x}}_{14}+a_{24}{\dot{x}}_{24}-a_{34}{\dot{x}}_{34}.\end{array}$$

(13)

Combining with (5), (10), and (11), then the synchronization error system (13) can be transformed into the following form:

$$\{\begin{array}{l}{\dot{e}}_1=a_{11}{x}_{12}+a_{21}{x}_{22}-a_{31}(x_{32}+u_1),\\ {\dot{e}}_2=a_{12}({\alpha }_1{x}_{13}-{\alpha }_2{x}_{12}-{\alpha }_3{x}_{11}^2{x}_{12})+a_{22}({\beta }_1{x}_{23}-{\beta }_2{x}_{22}-{\beta }_3{x}_{21}^2{x}_{22})\\ \phantom{{\dot{e}}_2=}-a_{32}({\gamma }_1{x}_{33}-{\gamma }_2{x}_{32}-{\gamma }_3{x}_{31}^2{x}_{32}+u_2),\\ {\dot{e}}_3=a_{13}({\alpha }_4{x}_{12}-{\alpha }_4{x}_{13}+{\alpha }_5{x}_{14})+a_{23}({\beta }_4{x}_{22}-{\beta }_4{x}_{23}+{\beta }_5{x}_{24})\\ \phantom{{\dot{e}}_3=}-a_{33}({\gamma }_4{x}_{32}-{\gamma }_4{x}_{33}+{\gamma }_5{x}_{34}+u_3),\\ {\dot{e}}_4=a_{14}(-{\alpha }_6{x}_{13}-{\alpha }_7{x}_{14})+a_{24}(-{\beta }_6{x}_{23}-{\beta }_7{x}_{24})-a_{34}(-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34}+u_4).\end{array}$$

(14)

Theorem 1 If the controller is chosen as

$$\{\begin{array}{l}{u}_1=\frac{1}{a_{31}}[a_{11}(x_{11}+x_{12})+a_{21}(x_{21}+x_{22})-a_{31}(x_{31}+x_{32})+a_{12}{x}_{12}-a_{14}{x}_{14}\\ \phantom{u_1=}+a_{22}{x}_{22}-a_{24}{x}_{24}-a_{32}{x}_{32}+a_{34}{x}_{34}],\\ u_2=\frac{1}{a_{32}}[a_{12}[{\alpha }_1{x}_{13}+(1-{\alpha }_2)x_{12}-{\alpha }_3{x}_{11}^2{x}_{12}]\\ \phantom{u_2=}+a_{22}[{\beta }_1{x}_{23}+(1-{\beta }_2)x_{22}-{\beta }_3{x}_{21}^2{x}_{22}]\\ \phantom{u_2=}-a_{32}[{\gamma }_1{x}_{33}+(1-{\gamma }_2)x_{32}-{\gamma }_3{x}_{31}^2{x}_{32}]-a_{11}{x}_{11}+a_{13}{x}_{13}-a_{21}{x}_{21}\\ \phantom{u_2=}+a_{23}{x}_{23}+a_{31}{x}_{31}-a_{33}{x}_{33}],\\ u_3=\frac{1}{a_{33}}[a_{13}[{\alpha }_4{x}_{12}+(1-{\alpha }_4)x_{13}+{\alpha }_5{x}_{14}]+a_{23}[{\beta }_4{x}_{22}+(1-{\beta }_4)x_{23}+{\beta }_5{x}_{24}]\\ \phantom{u_3=}-a_{33}[{\gamma }_4{x}_{32}+(1-{\gamma }_4)x_{33}+{\gamma }_5{x}_{34}]-a_{12}{x}_{12}+a_{14}{x}_{14}\\ \phantom{u_3=}-a_{22}{x}_{22}+a_{24}{x}_{24}+a_{32}{x}_{32}-a_{34}{x}_{34}],\\ u_4=\frac{1}{a_{34}}[a_{14}(-{\alpha }_6{x}_{13}-{\alpha }_7{x}_{14})+a_{24}(-{\beta }_6{x}_{23}-{\beta }_7{x}_{24})\\ \phantom{u_4=}-a_{34}(-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34})+a_{11}{x}_{11}-a_{13}{x}_{13}\\ \phantom{u_4=}+a_{14}{x}_{14}+a_{21}{x}_{21}-a_{23}{x}_{23}+a_{24}{x}_{24}-a_{31}{x}_{31}+a_{33}{x}_{33}-a_{34}{x}_{34}],\end{array}$$

(15)

then the driven systems (5) and (10) will achieve combination synchronization with the response system (11).

Proof Choose the following Lyapunov function:

$$V(e(t))=V(e_1,e_2,e_3,e_4)=\frac{1}{2}(e_1^2+e_2^2+e_3^2+e_4^2).$$

(16)

Calculating the upper right Dini-derivative $D^{+}V$ of V along with the trajectory of system (14), we have

$$\begin{array}{rl}{D}^{+}V=& e_1{\dot{e}}_1+e_2{\dot{e}}_2+e_3{\dot{e}}_3+e_4{\dot{e}}_4\\ =& e_1[a_{11}{x}_{12}+a_{21}{x}_{22}-a_{31}(x_{32}+u_1)]+e_2[a_{12}({\alpha }_1{x}_{13}-{\alpha }_2{x}_{12}-{\alpha }_3{x}_{11}^2{x}_{12})\\ +a_{22}({\beta }_1{x}_{23}-{\beta }_2{x}_{22}-{\beta }_3{x}_{21}^2{x}_{22})-a_{32}({\gamma }_1{x}_{33}-{\gamma }_2{x}_{32}-{\gamma }_3{x}_{31}^2{x}_{32}+u_2)]\\ +e_3[a_{13}({\alpha }_4{x}_{12}-{\alpha }_4{x}_{13}+{\alpha }_5{x}_{14})+a_{23}({\beta }_4{x}_{22}-{\beta }_4{x}_{23}+{\beta }_5{x}_{24})\\ -a_{33}({\gamma }_4{x}_{32}-{\gamma }_4{x}_{33}+{\gamma }_5{x}_{34}+u_3)]\\ +e_4[a_{14}(-{\alpha }_6{x}_{13}-{\alpha }_7{x}_{14})+a_{24}(-{\beta }_6{x}_{23}-{\beta }_7{x}_{24})\\ -a_{34}(-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34}+u_4)].\end{array}$$

(17)

Substituting (15) into (17), then

$$\begin{array}{rl}{D}^{+}V=& e_1[-(a_{11}{x}_{11}+a_{21}{x}_{21}-a_{31}{x}_{31})-(a_{12}{x}_{12}+a_{22}{x}_{22}-a_{32}{x}_{32})\\ +(a_{14}{x}_{14}+a_{24}{x}_{24}-a_{34}{x}_{34})]\\ +e_2[-(a_{12}{x}_{12}+a_{22}{x}_{22}-a_{32}{x}_{32})-(a_{13}{x}_{13}+a_{23}{x}_{23}-a_{33}{x}_{33})\\ +(a_{11}{x}_{11}+a_{21}{x}_{21}-a_{31}{x}_{31})]\\ +e_3[-(a_{13}{x}_{13}+a_{23}{x}_{23}-a_{33}{x}_{33})-(a_{14}{x}_{14}+a_{24}{x}_{24}-a_{34}{x}_{34})\\ +(a_{12}{x}_{12}+a_{22}{x}_{22}-a_{32}{x}_{32})]\\ +e_4[-(a_{14}{x}_{14}+a_{24}{x}_{24}-a_{34}{x}_{34})-(a_{11}{x}_{11}+a_{21}{x}_{21}-a_{31}{x}_{31})\\ +(a_{13}{x}_{13}+a_{23}{x}_{23}-a_{33}{x}_{33})]\\ =& e_1(-e_1-e_2+e_4)+e_2(-e_2-e_3+e_1)+e_3(-e_3-e_4+e_2)+e_4(-e_4-e_1+e_3)\\ =& -e_1^2-e_2^2-e_3^2-e_4^2\\ =& -e^{T}e,\end{array}$$

(18)

where $e={(e_1,e_2,e_3,e_4,e_5)}^T$.

Let $t>0$ be arbitrarily given, integrating the above equation (18) from 0 to t, then

$${\int }_0^t{\parallel e(s)\parallel }^2\mathrm{d}s={\int }_0^t-\dot{V}\mathrm{d}s=V(e(0))-V(e(t))\le V(e(0)),$$

where $\parallel \cdot \parallel$ is the Euclidean vector norm.

According to Barbalat’s lemma, we have ${\parallel e(t)\parallel }^2\to 0$ as $t\to +\mathrm{\infty }$. Hence, $(e_1,e_2,e_3,e_4)\to (0,0,0,0)$ as $t\to +\mathrm{\infty }$. It implies that the driven systems (5) and (10) can achieve combination synchronization with the response system (11). The proof is completed. □

Next, some corollaries can be directly derived from Theorem 1.

Corollary 1 If the controller is chosen as

$$\{\begin{array}{l}{u}_1=\frac{1}{a_{31}}[a_{11}(x_{11}+x_{12})-a_{31}(x_{31}+x_{32})+a_{12}{x}_{12}-a_{14}{x}_{14}-a_{32}{x}_{32}+a_{34}{x}_{34}],\\ u_2=\frac{1}{a_{32}}[a_{12}[{\alpha }_1{x}_{13}+(1-{\alpha }_2)x_{12}-{\alpha }_3{x}_{11}^2{x}_{12}]-a_{32}[{\gamma }_1{x}_{33}+(1-{\gamma }_2)x_{32}-{\gamma }_3{x}_{31}^2{x}_{32}]\\ \phantom{u_2=}-a_{11}{x}_{11}+a_{13}{x}_{13}+a_{31}{x}_{31}-a_{33}{x}_{33}],\\ u_3=\frac{1}{a_{33}}[a_{13}[{\alpha }_4{x}_{12}+(1-{\alpha }_4)x_{13}+{\alpha }_5{x}_{14}]-a_{33}[{\gamma }_4{x}_{32}+(1-{\gamma }_4)x_{33}+{\gamma }_5{x}_{34}]\\ \phantom{u_3=}-a_{12}{x}_{12}+a_{14}{x}_{14}+a_{32}{x}_{32}-a_{34}{x}_{34}],\\ u_4=\frac{1}{a_{34}}[a_{14}(-{\alpha }_6{x}_{13}-{\alpha }_7{x}_{14})-a_{34}(-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34})+a_{11}{x}_{11}-a_{13}{x}_{13}+a_{14}{x}_{14}\\ \phantom{u_4=}-a_{31}{x}_{31}+a_{33}{x}_{33}-a_{34}{x}_{34}],\end{array}$$

then the driven system (5) will achieve complete synchronization with the response system (11).

Corollary 2 If the controller is chosen as

$$\{\begin{array}{l}{u}_1=\frac{1}{a_{31}}[a_{21}(x_{21}+x_{22})-a_{31}(x_{31}+x_{32})+a_{22}{x}_{22}-a_{24}{x}_{24}-a_{32}{x}_{32}+a_{34}{x}_{34}],\\ u_2=\frac{1}{a_{32}}[a_{22}[{\beta }_1{x}_{23}+(1-{\beta }_2)x_{22}-{\beta }_3{x}_{21}^2{x}_{22}]-a_{32}[{\gamma }_1{x}_{33}+(1-{\gamma }_2)x_{32}-{\gamma }_3{x}_{31}^2{x}_{32}]\\ \phantom{u_2=}-a_{21}{x}_{21}+a_{23}{x}_{23}+a_{31}{x}_{31}-a_{33}{x}_{33}],\\ u_3=\frac{1}{a_{33}}[a_{23}[{\beta }_4{x}_{22}+(1-{\beta }_4)x_{23}+{\beta }_5{x}_{24}]-a_{33}[{\gamma }_4{x}_{32}+(1-{\gamma }_4)x_{33}+{\gamma }_5{x}_{34}]\\ \phantom{u_3=}-a_{22}{x}_{22}+a_{24}{x}_{24}+a_{32}{x}_{32}-a_{34}{x}_{34}],\\ u_4=\frac{1}{a_{34}}[a_{24}(-{\beta }_6{x}_{23}-{\beta }_7{x}_{24})-a_{34}(-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34})\\ \phantom{u_4=}+a_{21}{x}_{21}-a_{23}{x}_{23}+a_{24}{x}_{24}-a_{31}{x}_{31}+a_{33}{x}_{33}-a_{34}{x}_{34}],\end{array}$$

then the driven system (10) will achieve complete synchronization with the response system (11).

Corollary 3 If the controller is chosen as

$$\{\begin{array}{l}{u}_1=\frac{1}{a_{31}}[-a_{31}(x_{31}+x_{32})-a_{32}{x}_{32}+a_{34}{x}_{34}],\\ u_2=\frac{1}{a_{32}}[-a_{32}[{\gamma }_1{x}_{33}+(1-{\gamma }_2)x_{32}-{\gamma }_3{x}_{31}^2{x}_{32}]+a_{31}{x}_{31}-a_{33}{x}_{33}],\\ u_3=\frac{1}{a_{33}}[-a_{33}[{\gamma }_4{x}_{32}+(1-{\gamma }_4)x_{33}+{\gamma }_5{x}_{34}]+a_{32}{x}_{32}-a_{34}{x}_{34}],\\ u_4=\frac{1}{a_{34}}[-a_{34}(-{\gamma }_6{x}_{33}-{\gamma }_7{x}_{34})-a_{31}{x}_{31}+a_{33}{x}_{33}-a_{34}{x}_{34}],\end{array}$$

then system (11) is asymptotically stabilizable.

Remark 3 The results obtained in Theorem 1 and Corollaries 1-3 either yield new, or extend, to a large extent, most of the existing results. To the best of our knowledge, few authors have considered synchronization control of the hyperchaotic memristor oscillator system. In fact, the control design of hyperchaotic memristor oscillator system is necessary and rewarding, in order to understand the memristive dynamics.

4 An illustrative example

In this section, a numerical example is given to verify the feasibility and effectiveness of the proposed control technique via computer simulations.

Assuming that parameters ${\alpha }_1={\beta }_1={\gamma }_1=16.4$, ${\alpha }_2={\beta }_2={\gamma }_2=-3.28$, ${\alpha }_3={\beta }_3={\gamma }_3=19.68$, ${\alpha }_4={\beta }_4={\gamma }_4=1$, ${\alpha }_5={\beta }_5={\gamma }_5=1$, ${\alpha }_6={\beta }_6={\gamma }_6=15$, ${\alpha }_7={\beta }_7={\gamma }_7=0.5$, the scaling matrices $A_1=diag(a_{11},a_{12},a_{13},a_{14})=diag(1,1,1,1)$, $A_2=diag(a_{21},a_{22},a_{23},a_{24})=diag(1,1,1,1)$, $A_3=diag(a_{31},a_{32},a_{33},a_{34})=diag(1,1,1,1)$, the controller is chosen as

$$\{\begin{array}{l}{u}_1=x_{11}+2x_{12}-x_{14}+x_{21}+2x_{22}-x_{24}-x_{31}-2x_{32}+x_{34},\\ u_2=17.4x_{13}+4.28x_{12}-19.68x_{11}^2{x}_{12}+17.4x_{23}+4.28x_{22}-19.68x_{21}^2{x}_{22}\\ \phantom{u_2=}-17.4x_{33}-4.28x_{32}+19.68x_{31}^2{x}_{32}-x_{11}-x_{21}+x_{31},\\ u_3=2x_{14}+2x_{24}-2x_{34},\\ u_4=x_{11}-16x_{13}+0.5x_{14}+x_{21}-16x_{23}+0.5x_{24}-x_{31}+16x_{33}-0.5x_{34},\end{array}$$

according to Theorem 1, then the driven systems (5) and (10) will achieve combination synchronization with the response system (11). Figures 6-9 depict the time response of the synchronization error $e={(e_1,e_2,e_3,e_4)}^T$.

Figure 6

Time response curve for synchronization error ${\mathit{e}}_{\mathbf{1}}$ .

Figure 7

Time response curve for synchronization error ${\mathit{e}}_{\mathbf{2}}$ .

Figure 8

Time response curve for synchronization error ${\mathit{e}}_{\mathbf{3}}$ .

Figure 9

Time response curve for synchronization error ${\mathit{e}}_{\mathbf{4}}$ .

It is worth pointing out that the result in the above numerical example cannot be obtained by using any existing results.

5 Concluding remarks

This paper has introduced a hyperchaotic memristor oscillator system and presented a novel control method using combination scheme to drive two memristor oscillator systems to synchronize one response memristor oscillator system. The resulting hyperchaos synchronization via combination scheme is also verified by computer simulations. It is believed that the derived results and analytical techniques have great potential in controlling various hyperchaotic systems and hyperchaotic circuits, which open up a wide area for further research of chaos and hyperchaos memristive dynamics.