Abstract
The dynamical behaviors of a discrete-time SIS epidemic model are investigated in this paper. The result indicates that the model undergoes a flip bifurcation and a Hopf bifurcation, as found by using the center manifold theorem and bifurcation theory. Numerical simulations not only illustrate our results, but they also exhibit the complex dynamical behaviors, such as the period-doubling bifurcation in period-2, -4, -8, quasi-periodic orbits and the chaotic sets. Specifically, when the parameters A, , , r, λ are fixed at some values and the bifurcation parameter h changes with different values, there exist local stability, Hopf bifurcation, 3-periodic orbits, 7-periodic orbits, period-doubling bifurcation and chaotic sets. These results reveal far richer dynamical behaviors of the discrete epidemic model compared with the continuous epidemic models although the discrete epidemic model is simple. Finally, the feedback control method is used to stabilize chaotic orbits at an unstable endemic equilibrium.
Similar content being viewed by others
1 Introduction
In the theoretical studies of epidemic dynamical models, there are two kinds of mathematical models: the continuous-time models described by differential equations, and the discrete-time models described by difference equations. Recent years, the discrete-time epidemic models have been discussed in many papers. Usually, there are two ways to construct a discrete-time epidemic model: (i) by directly making use of the property of the epidemic disease (see [1, 2]), and (ii) by discretizing a continuous-time epidemic model using techniques, such as the forward Euler scheme and Mickens’ non-standard discretization (see [3]). In [3] the authors firstly used the non-standard or Mickens-type discretization in an explicitly epidemiological context. The details of Mickens-type discretization can be found in [4, 5].
Up to now, some work has been done on discrete-time epidemic models (for examples, see [6–21] and the references cited therein). These works mainly focused on the computation of the basic reproduction number; the local stability and global stability of the disease-free equilibrium and the endemic equilibrium; the extinction and persistence of the disease. The authors in [6–9] discussed the stabilities of the disease-free equilibrium and the endemic equilibrium for some SI, SIS, SIR, and SIRS type discrete-time epidemic models. In [9] we obtained the conditions for the existence and local stability of the disease-free equilibrium and endemic equilibrium in a class of discrete SIRS epidemic with three dimensions. The oscillation and stability have been discussed in [10–14]. The authors in [10, 11, 14] all used the non-standard discretization way to obtain their discrete epidemic models. Sufficient conditions for the global dynamics of the solution of the discrete SIRS epidemic model were obtained as for the original continuous model in [14]. A new way to study the basic reproduction number for some discrete-time epidemic models has been given in [15]. Li and Wang in [16] discussed the dynamical behaviors including a bifurcation, but not giving a proof of the bifurcation.
In general, the discrete epidemic models obtained by Mickens-type discretization have the same features as the original continuous-time model [10, 11, 14]. For the Rössler system [3], the difference equations obtained by the non-standard or Mickens-type method also show that the solutions to the discrete models are topologically equivalent to the solutions of the continuous-time system as long as the time step is less than a threshold value. For the discrete population models [22–24] approached by the forward Euler scheme, there existed a flip bifurcation, a Hopf bifurcation and chaos dynamical behaviors which are different from the dynamical behaviors in the corresponding continuous-time models. In [9] the authors used the forward Euler scheme to obtain a class of discrete SIRS epidemic models. They claimed that when the time step h is small () the dynamical behaviors are similar with the continuous-time model, and when the time step h is increasing () in the discrete epidemic model appears a flip bifurcation, a Hopf bifurcation, chaos, and more complex dynamical behaviors by the numerical simulations.
Therefore, motivated by the above studies, we will focus on the complex dynamical behaviors of a simple discrete SIS epidemic model approached by the forward Euler scheme. Now, we consider the following continuous-time SIS epidemic model described by differential equations:
where , and denote the numbers of susceptible, infective, individuals at time t, respectively. A is the recruitment rate of the population, is the natural death rate of the population, is the death rate of infective individuals which includes the natural death rate and the disease-related death rate, r is the recovery rate of the infective individuals, λ is the standard incidence rate. It is clear that [25] model (1) has the basic reproduction number , and if , then the disease-free equilibrium of model (1) is globally asymptotically stable, and if , then the endemic equilibrium of model (1) is locally asymptotically stable.
Applying the forward Euler scheme to model (1), we obtain the following discrete-time SIS epidemic model:
where h is the time step size. A, λ, , , and r are defined as model (1). It is assumed that initial values , and all the parameters are positive.
In this paper, we will study the existence of the disease-free equilibrium and endemic equilibrium, and the stability of the disease-free equilibrium and the endemic equilibrium for model (2). For detecting the complex dynamical behaviors, the time step h is selected as a bifurcation parameter in model (2). Furthermore, we use the numerical simulations to display the flip bifurcation, the Hopf bifurcation and complex dynamical behaviors. Finally, the chaos control for model (2) is obtained by the feedback control method.
The following is the organization of this paper. In the second section, we discuss the existence and local stability of equilibria in model (2). In the third section, we study the flip bifurcation and the Hopf bifurcation of model (2) by choosing h as a bifurcation parameter. In the fourth section, we present the numerical simulations, which not only illustrate our results with the theoretical analysis, but we also exhibit the complex dynamical behaviors such as the cascade of period-doubling bifurcation in period-2, 4, 8, quasi-periodic orbits, 3-periodic orbits, 7-periodic orbits and chaotic sets. In the fifth section, the feedback control method is used to control chaotic orbits at an unstable endemic equilibrium. The conclusion is given in the last section.
2 Analysis of equilibria
Let (the basic reproductive rate), and we have the following result as regards the existence of the equilibria of model (2).
Lemma 2.1
-
(1)
If , then model (2) has only the disease-free equilibrium .
-
(2)
If , then model (2) has two equilibria: the disease-free equilibrium and the endemic equilibrium , where
Now, we study the stability of equilibria and of model (2). The Jacobian matrix of model (2) at the equilibrium is
The corresponding characteristic equation of can be written as
After simple computing, we obtain the local stability result of the disease-free equilibrium , which is shown in the following.
Theorem 2.1 If , then
-
(1)
is a sink if ;
-
(2)
is a source if ;
-
(3)
is non-hyperbolic if , or ;
-
(4)
is a saddle if , or .
On the local stability of equilibrium , we have the following result.
Theorem 2.2 If , then
-
(1)
is a sink if one of the following conditions holds:
-
(A)
and ;
-
(B)
and ;
-
(2)
is a source if one of the following conditions holds:
-
(A)
and ;
-
(B)
and ;
-
(3)
is non-hyperbolic if one of the following conditions holds:
-
(A)
and or ;
-
(B)
and ;
-
(4)
is a saddle if the following condition holds:
and ,
where
and
The proofs of Theorem 2.1 and Theorem 2.2 are simple and hence we omit them.
From the above discussion we find that if condition (A) in conclusion (3) of Theorem 2.2 holds, then one of the two eigenvalues of the matrix is −1 and the other is neither 1 nor −1. We can rewrite conditions (A) in the following form:
where
and
In the following section we will see that there may be a flip bifurcation round equilibrium if h varies in the small neighborhood of or and or .
When condition (B) in conclusion (3) of Theorem 2.2 holds, we can see that the two eigenvalues of the matrix are a pair of conjugate complex numbers, the modules of which are 1. Condition (B) can be written in following form:
where
In the following section we will see that the Hopf bifurcation round equilibrium will appear if h varies in the small neighborhood of and .
3 Analysis of bifurcation
For a function , we denote by , , and the first order partial derivative, the second order partial derivative and the third order partial derivative of with respect to , and , respectively.
Based on the analysis in Section 2, in this section we choose the step size h as the bifurcation parameter to study the flip bifurcation and Hopf bifurcation of by using the center manifold theorem and bifurcation theory in [26, 27].
We firstly discuss the flip bifurcation of model (2) at the equilibrium when h varies in the small neighborhood of and . For the case in which h varies in the small neighborhood of and , we can give a similar argument.
Taking the parameters arbitrarily, then giving a perturbation of parameter h, we consider model (2) with perturbation as follows:
where .
Let and , then we transform the equilibrium of model (4) into the origin. By calculating we obtain
Expanding model (5) as a Taylor series at to the second order, it becomes the following model:
where
Let a matrix be defined:
then T is invertible. Using translation
then model (6) becomes of the following form:
where
and
Now, we determine the center manifold of model (7) at the equilibrium in a small neighborhood of . By the center manifold theorem, we can obtain the approximate representation of the center manifold as follows:
where is a function in at least of the third order, and
Therefore, on the center manifold we have
Hence,
Furthermore, we have
where
Therefore, when model (7) is restricted to the center manifold we obtain the map as follows:
In order to undergo a flip bifurcation for map (8), we require that the two discriminatory quantities and are not zero, where
and
Therefore, by the above analysis and the theorem in [26], we obtain the following result.
Theorem 3.1 If , then model (4) undergoes a flip bifurcation at the equilibrium when the parameter varies in a small neighborhood of the origin. Moreover, if (resp., ), then the period-2 points which bifurcate from are stable (resp., unstable).
Finally, we discuss the Hopf bifurcation of if h varies in the small neighborhood of N. We take the parameters arbitrarily. We consider a small perturbation of (2) by choosing the bifurcation parameter as follows:
where which is a small perturbation.
Let and , then we transform equilibrium into the origin, we have
The characteristic equation associated with the linearization of model (10) at is the following:
where
Correspondingly, when varies in a small neighborhood of the roots of the characteristic equation are
and we have
Moreover, it is required that when , , , which is equivalent to . Note and , then
Hence,
We only need to require that , i.e.,
Therefore, the eigenvalues do not lie in the intersection of the unit circle with the coordinate axes when and (11) holds.
In the following, we study the normal form of model (10) when . Expanding model (10) as a Taylor series at , to third order, then it becomes the following model:
where (; ) have the same form as in model (6), but in model (12) and
Let
and
then T is invertible. Using translation
then model (10) becomes of the following form:
where
and
Furthermore,
and
In order for model (15) to undergo a Hopf bifurcation, we require that the following discriminatory quantity is not zero [27]:
where
Moreover,
where
Therefore, from the above analysis and Theorem 3.5.2 in [27] we have the following result.
Theorem 3.2 If condition (11) holds and , then model (9) undergoes a Hopf bifurcation at the equilibrium when the parameter changes in the small neighborhood of the origin. Moreover, if (resp., ), then an attracting (resp., repelling) invariant closed curve bifurcates from for (resp., ).
4 Numerical simulation
In this section, we give the bifurcation diagrams and phase portraits of model (2) to confirm the above theoretical analysis and show the new interesting complex dynamical behaviors by using numerical simulations.
The bifurcation diagrams are considered in the following two cases.
Case 1. We choose , , , , , and in model (2).
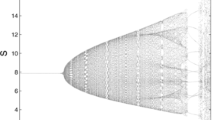
By calculating, we find that model (2) has an unique endemic equilibrium , , , , and . Obviously, we have . Figures 1 and 2 show the correctness of Theorem 3.1.
From Figures 1 and 2 we see that the equilibrium is stable for and loses its stability when ; when , there is a period-doubling bifurcation. Moreover, a chaotic set emerges with the increasing of h. The corresponding phase portraits for various values of h are showed in Figure 3.
Case 2. We choose , , , , , , and in model (2).
By calculating, we see that model (2) has a unique endemic equilibrium , , , and . Obviously, we have . Figure 4 shows the correctness of Theorem 3.2.
From Figure 4 we find that endemic equilibrium of model (2) is stable for , and it loses its stability when ; Moreover, when then an invariant circle appears; when , there exist 16-period orbits; when , there exist 32-period orbits; when , there exist period-bifurcation and chaotic sets; when , there exist 7-period orbits; when , there exist period-bifurcation and chaotic sets; when , there exist 3-period orbits; with the increasing of h, the period bifurcation and chaotic sets appear again. The above results can be seen from the phase portraits in Figure 5(A)-(L) corresponding to Figure 4.
The phase portraits of model ( 2 ) for different values of h corresponding to Figure 4. Here (A) is for , (B) is for , (C) is for , (D) is for , (E) is for , (F) is for , (G) is for , (H) is for , (I) is for , (J) is for , (K) is for , and (L) is for .
Remark 1 For the discrete model (2), the 3-period orbits, 7-period orbits and complex dynamical behaviors are obtained in this paper which reveal far richer dynamical behaviors than the continuous epidemic model (1).
5 Chaos control
In this section, the feedback control method is used to stabilize chaotic orbits at an unstable endemic equilibrium of model (2).
Consider the following controlled form of model (2):
with the following feedback control law as the control force:
where is the feedback gain, is endemic equilibrium of model (2).
The Jacobian matrix of model (15) at endemic equilibrium is
where , , , are given in model (6).
The corresponding characteristic equation of matrix is
Let is the eigenvalue of (17), then
and
The lines of marginal stability are determined by solving the equation and . These conditions guarantee that the eigenvalues and have modulus less than 1.
Suppose ; from (19) we have line as follows:
Suppose ; from (18), (19) we have lines and as follows:
and
The stable eigenvalues lie within a triangular region by line , , and , which can be seen from Figure 6.
Therefore, some numerical simulations can be made to control the unstable endemic equilibrium by the state feedback method. The parameters are selected as , , , , , , and the feedback gain , . A chaotic trajectory is stabilized at the endemic equilibrium (see Figure 7).
Remark 2 In [16, 28] the authors only obtained the chaotic sets. In this paper, the feedback control method is used to stabilize chaotic orbits at an unstable endemic equilibrium. As Chen and Sun in [29] pointed out the feedback control variables have an important role in dealing with the disease and no scholar has investigated the feedback control in epidemic models. They only discussed a continuous-time SI epidemic model with feedback controls. We use the feedback control method to stabilize the chaotic orbits in a discrete-time SIS epidemic model. These results show that the feedback control may be a useful way to control the disease at an acceptable level in the population.
6 Conclusion
In this paper, we discuss the dynamical behaviors of model (2). The basic reproductive rate is obtained with the value . If , model (2) only has a disease-free equilibrium ; if , model (2) has an endemic equilibrium besides , and when for the parameter h are chosen different values, model (2) appears to have many complex and interesting dynamical behaviors. That is, if the parameters are in , or N and taking h as the bifurcation parameter, there appear a flip bifurcation and a Hopf bifurcation for model (2), respectively. Moreover, model (2) displays very complex dynamical behaviors, such as invariant cycle, cascade period-doubling, 3-period orbits, 7-period orbits, and chaotic sets. In Section 5, the chaos control is obtained. However, we only control the chaotic orbits to the endemic equilibrium . For the epidemic disease, we hope that the infective individuals become extinct, that is, .
In the discrete process of the continuous models, there are two possible approaches: the Mickens scheme [3, 10, 11, 14] and the Euler scheme [9, 22–24]. As the authors of [3, 10, 11, 14] proved, the discrete epidemic models which are obtained by the Mickens scheme always have the same dynamical behaviors of the corresponding continuous models. The models [9, 22–24] obtained by the forward Euler scheme show complex dynamical behaviors, which are different from the continuous models. In our study, we only focus on the complex dynamical behaviors and chaos control of our discrete SIS epidemic model; we are not to discuss the advantages or disadvantages comparing the forward Euler scheme with the Mickens scheme. By the Mickens scheme, we will obtain another discrete model from model (1). Whether the discrete model has the same dynamical behaviors as the continuous model (1) we will study in our future study.
Finally, the results show that the susceptible and infective individuals can coexist in stable period-n orbits and cycle (see Figures 3 and 5). Moreover, we obtained the chaos control in model (2) which can help us to control the disease transmitting in a population. The above arguments indicate that our findings can give a better understanding of the complex dynamical behaviors of the disease and provide a useful way to control the disease, in spite of the lack of some real data for our model. In our future work, we expect to obtain some more results based on real data from known epidemic diseases to illustrate the validity of our theoretical results, such as how to predict the occurrence of diseases, in which way do bifurcations, chaos, and strange attractors impact on the dynamics of disease, and so on.
References
Franke JE, Yakubu AA: Disease-induced mortality in density-dependent discrete-time SIS epidemic models. Math. Biosci. 2008, 57: 755-790.
Castillo-Chavez C, Yakubu AA: Discrete-time SIS models with complex dynamics. Nonlinear Anal. 2001, 47: 4753-4762. 10.1016/S0362-546X(01)00587-9
Willox R, Grammaticos B, Carstea AS, Ramani A: Epidemic dynamics: discrete-time and cellular automaton models. Physica A 2003, 328: 13-22. 10.1016/S0378-4371(03)00552-1
Mickens RE: Discretizations of nonlinear differential equations using explicit nonstandard methods. J. Comput. Appl. Math. 1999, 110: 181-185. 10.1016/S0377-0427(99)00233-2
Letellier C, Elaydi S, Aguirre L, Alaoui A: Difference equations versus differential equations, a possible equivalence for the Rössler system. Physica D 2004, 195: 29-49. 10.1016/j.physd.2004.02.007
Li J, Ma Z, Brauer F: Global analysis of discrete-time SI and SIS epidemic models. Math. Biosci. 2007, 4: 699-710.
Zhou Y, Ma Z, Brauer F: A discrete epidemic model for SARS transmission and control in China. Math. Comput. Model. 2004, 40: 1491-1506. 10.1016/j.mcm.2005.01.007
Li J, Lou J, Lou M: Some discrete SI and SIS epidemic models. Appl. Math. Mech. 2008, 29: 113-119. 10.1007/s10483-008-0113-y
Hu Z, Teng Z, Jiang H: Stability analysis in a class of discrete SIRS epidemic models. Nonlinear Anal., Real World Appl. 2012, 13: 2017-2033. 10.1016/j.nonrwa.2011.12.024
Ramani A, Carstea AS, Willox R, Grammaticos B: Oscillating epidemics: a discrete-time model. Physica A 2004, 333: 278-292.
Satsuma J, Willox R, Ramani A, Grammaticos B, Carstea AS: Extending the SIR epidemic model. Physica A 2004, 336: 369-375. 10.1016/j.physa.2003.12.035
Zhang D, Shi B: Oscillation and global asymptotic stability in a discrete epidemic model. J. Math. Anal. Appl. 2003, 278: 194-202. 10.1016/S0022-247X(02)00717-5
D’Innocenzo A, Paladini F, Renna L: A numerical investigation of discrete oscillating epidemic models. Physica A 2006, 364: 497-512.
Sekiguchi M, Ishiwata E: Global dynamics of a discretized SIRS epidemic model with time delay. J. Math. Anal. Appl. 2010, 371: 195-202. 10.1016/j.jmaa.2010.05.007
Allen LJS, Driessche P: The basic reproduction number in some discrete-time epidemic models. J. Differ. Equ. Appl. 2008, 14: 1127-1147. 10.1080/10236190802332308
Li X, Wang W: A discrete epidemic model with stage structure. Chaos Solitons Fractals 2005, 26: 947-958. 10.1016/j.chaos.2005.01.063
Mendez V, Fort J: Dynamical evolution of discrete epidemic models. Physica A 2000, 284: 309-317. 10.1016/S0378-4371(00)00210-7
Allen LJS: Some discrete-time SI, SIR, and SIS epidemic models. Math. Biosci. 1994, 124: 83-105. 10.1016/0025-5564(94)90025-6
Franke JE, Yakubu AA: Disease-induced mortality in density-dependent discrete-time S-I-S epidemic models. J. Math. Biol. 2008, 57: 755-790. 10.1007/s00285-008-0188-9
Allen LJS, Lou Y, Nevai AL: Spatial patterns in a discrete-time SIS patch model. J. Math. Biol. 2009, 58: 339-375. 10.1007/s00285-008-0194-y
Hu, Z, Teng, Z: Permanence and extinction analysis of a discrete SIRS epidemic model with standard incidence. Acta Math. Appl. Sin. (2011, submitted)
Ghaziani PK, Govaerts W, Sonck C: Resonance and bifurcation in a discrete-time predator-prey system with Holling functional response. Nonlinear Anal., Real World Appl. 2012, 13: 1451-1465. 10.1016/j.nonrwa.2011.11.009
Hu Z, Teng Z, Zhang L: Stability and bifurcation analysis of a discrete predator-prey model with nonmonotonic functional response. Nonlinear Anal., Real World Appl. 2011, 12: 2356-2377. 10.1016/j.nonrwa.2011.02.009
He Z, Lai X: Bifurcation and chaotic behavior of a discrete-time predator-prey system. Nonlinear Anal., Real World Appl. 2011, 12: 403-417. 10.1016/j.nonrwa.2010.06.026
Ma Z, Zhou Y, Wang W: Mathematical Models and Studies in Epidemic Dynamics. Kexue Publication, Beijing; 2004.
Robinson C: Dynamical Models, Stability, Symbolic Dynamics and Chaos. 2nd edition. CRC Press, Boca Raton; 1999.
Guckenheimer J, Holmes P: Nonlinear Oscillations, Dynamical Model and Bifurcation of Vector Fields. Springer, New York; 1983.
Liu X, Xiao D: Complex dynamic behaviors of a discrete-time predator-prey system. Chaos Solitons Fractals 2007, 32: 80-94. 10.1016/j.chaos.2005.10.081
Chen L, Sun J: Global stability of an SI epidemic model with feedback controls. Appl. Math. Lett. 2014, 28: 53-55.
Acknowledgements
The authors are very grateful to the editor and anonymous referees for their valuable comments and helpful suggestions, which led to a substantial improvement of the original manuscript. This study was supported by the National Natural Science Foundation of P.R. China (11271312, 11361059, 10901130), Natural Science Foundation of Xinjiang Province of China (2012211B07), the Scientific Research Programmes of Colleges in Xinjiang XJEDU2013I03.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, Z., Teng, Z., Jia, C. et al. Dynamical analysis and chaos control of a discrete SIS epidemic model. Adv Differ Equ 2014, 58 (2014). https://doi.org/10.1186/1687-1847-2014-58
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-58