Abstract
In this paper, the exponential stability of bidirectional associative memory neural networks with leakage time-varying delays and sampled-data state feedback input is considered. By applying the time-delay approach, some conditions for ensuring the stability of a system are obtained. In addition, a numerical example is given to demonstrate the effectiveness of the obtained results.
Similar content being viewed by others
1 Introduction
In the past few decades, neural networks have been widely investigated by researchers. In 1987, bidirectional associative memory (BAM) neural networks were firstly introduced by Kosko [1, 2]. Due to its better abilities as information associative memory, the BAM neural network has attracted considerable attention in different fields such as signal processing, pattern recognition, optimization, and so on.
It is well known that time delay is unavoidable in the hardware implementation of neural networks due to the finite switching speed of neurons and amplifiers. The delay can cause instability, oscillation, or poor dynamical behavior. In practical applications, there exist many types of time delays such as discrete delays [3], time-varying delays [4], distributed delays [5, 6], random delays [7] and leakage delays (or forgetting delays) [8, 9]. Up to now, a large number of results about delay BAM neural networks have been reported [10–13]. All of the conclusions could be roughly summarized into two types: in terms of the stability analysis of equilibrium points, and of the existence and stability of periodic or almost periodic solutions.
The leakage delay, which exists in the negative feedback term of a neural network system, emerges as a research topic of primary importance recently. Gopalsamy [8] investigated the stability of the BAM neural networks with constant leakage delays. Further, Liu [14] discussed the global exponential stability for BAM neural networks with time-varying leakage delays, which extend and improve the main results of Gopalsamy. Peng et al. [15–17] derived the stability criteria for the BAM neural networks with leakage delays, unbounded distributed delays and probabilistic time-varying delays.
Sampled-data state feedback is a practical and useful control scheme and has been studied extensively over the past decades. There are some results dealing with synchronization [18, 19], state estimate [20–22] and stability [23–29]. Recently, the work in [24] has studied the problem of the stability of sampled-data piecewise affine systems via the input delay approach. Although the importance of the stability of neural networks has been widely recognized, no related results have been established for the sampled-data stability of BAM neural networks with leakage time-varying delays. Motivated by the works above, we consider the sampled-data stability of BAM neural networks with leakage time-varying delays under variable sampling with a known upper bound on the sampling intervals.
The organization of this paper is as follows. In Section 2, the problem is formulated and some basic preliminaries and assumptions are given. The main results are presented in Section 3. In Section 4, a numerical example is given to demonstrate the effectiveness of the obtained results. Some conclusions are proposed in Section 5.
2 Preliminaries
In this paper, we consider the following BAM neural networks with leakage time-varying delays and sampled-data state feedback inputs:
where , the and are neuron state variables, the positive constants and denote the time scales of the respective layers of the networks, , , , are connection weights of the network. and denote the leakage delays, and are time-varying delays, , are neuron activation functions, , are sampled-data state feedback inputs, denotes the sample time point, , , ℕ denotes the set of all natural numbers.
Assume that there exists a positive constant L such that the sample interval , . Let , for , then with .
For the sake of convenience, we give the following notations:
Before ending this section, we introduce two assumptions, which will be used in next section.
Assumption 1 There exist constants , such that
for all , and .
Assumption 2 Let , , for all . There exist positive constants and such that, for and , the following inequalities hold:
3 Main results
In this section, we investigate the exponential stability of (1). By using the input delay approach [24], (1) can be rewritten in the following form:
The initial conditions of (3) are: , , , , where and are continuous functions on .
The main results are stated as follows.
Theorem 1 Let Assumptions 1 and 2 hold; then the BAM neural network (3) is exponentially stable, i.e., there exists a positive constant λ such that , , .
Proof Define the continuous functions
where , .
By Assumption 2, we have
Because and are continuous functions, we can choose a small positive constant λ such that, for all ,
Let
Calculating the derivative of and along the solution of (3), we have
and
We define a positive constant M as follows:
Let K be a positive number such that
Now, we will prove that
Let , we firstly prove
In fact, if it is not valid, there exist , such that at least one of the following cases occurs:
For , ,
Hence
Similarly, we have
If (a) holds, we get
which contradicts (a).
If (b) holds, we get
This is a contradiction with (b).
Similarly, if (c) or (d) holds, we can also derive contradictory results with respect to (c) or (d), respectively. So (9) is correct. From (7) and (9), we have
Next, we will prove
If it is not like this, there exist , such that one of the following cases occurs:
Similar to the proof of (9), we can deduce that (13) holds. Combining (9) and (13), we have
Using mathematical induction, the inequalities (8) hold. By a similar proof to (11), we have , , for , which implies , , . This completes the proof. □
Remark 2 If the leakage delays in (3) are constant, that is, , . Assumption 2 is changed into the following form.
Assumption 2′ Let , , for all . There exist positive constants and such that, for and , the following conditions hold:
Similar to the proof of Theorem 1, we get the following result.
Corollary 1 If Assumptions 1 and 2′ hold, the BAM neural networks with constant leakage delays and the sampled-data state feedback inputs are exponentially stable.
4 Simulation example
In this section, we give an illustrative example to show the efficiency of our theoretical results.
Example 1 Consider the following BAM neural network with leakage delays and sampled-data state feedback inputs:
where
and the sampled-data gain
The activation functions are taken as . Time-varying delays are chosen as , and the leakage delays are chosen as , , respectively.
It is easy to verify , . Select , , , and we obtain
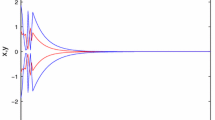
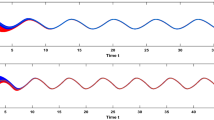
This means that all conditions in Theorem 1 are satisfied. Hence, by Theorem 1 (17) is exponentially stable. On the other hand, we have the following simulation result, shown in Figure 1.
State trajectory of the system [17].
5 Conclusion
In this paper, we investigate the stability of BAM neural networks with leakage delays and a sampled-data input. By using the time-delay approach, the conditions for ensuring the exponential stability of the system are derived. It should be pointed out that there are many papers focusing on the stability problem of sampled-data systems, leakage delay, and sampled-data state feedback that have never been taken into consideration in the BAM neural networks. To the best of our knowledge, this is the first time to consider the stability of BAM neural networks with both leakage delays and sampled-data state feedback at the same time. The results of this paper are worthy as complementary to the existing results. Finally, a numerical example and its computer simulations have been presented to show the effectiveness of our theoretical results.
References
Kosko B: Adaptive bi-directional associative memories. Appl. Opt. 1987, 26: 4947-4960. 10.1364/AO.26.004947
Kosko B: Bi-directional associative memories. IEEE Trans. Syst. Man Cybern. 1988, 18: 49-60. 10.1109/21.87054
Gao M, Cui B: Global robust exponential stability of discrete-time interval BAM neural networks with time-varying delays. Appl. Math. Model. 2009, 33(3):1270-1284. 10.1016/j.apm.2008.01.019
Ailong W, Zhigang Z: Dynamic behaviors of memristor-based recurrent neural networks with time-varying delays. Neural Netw. 2012, 36: 1-10.
Wang Z, Zhang H: Global asymptotic stability of reaction-diffusion Cohen-Grossberg neural networks with continuously distributed delays. IEEE Trans. Neural Netw. 2010, 21(1):39-48.
Li Y, Yang C: Global exponential stability analysis on impulsive BAM neural networks with distributed delays. J. Math. Anal. Appl. 2006, 324(2):1125-1139. 10.1016/j.jmaa.2006.01.016
Lou X, Ye Q, Cui B: Exponential stability of genetic regulatory networks with random delays. Neurocomputing 2010, 73: 759-769. 10.1016/j.neucom.2009.10.006
Gopalsamy K: Leakage delays in BAM. J. Math. Anal. Appl. 2007, 325: 1117-1132. 10.1016/j.jmaa.2006.02.039
Zhang H, Shao J: Existence and exponential stability of almost periodic solutions for CNNs with time-varying leakage delays. Neurocomputing 2013, 74: 226-233.
Arik S, Tavsanoglu V: Global asymptotic stability analysis of bidirectional associative memory neural networks with constant time delays. Neurocomputing 2005, 68: 161-176.
Cao J, Wang L: Periodic oscillatory solution of bidirectional associative memory networks with delays. Phys. Rev. E 2000, 61: 1825-1828.
Liu Z, Chen A, Cao J: Existence and global exponential stability of almost periodic solutions of BAM neural networks with distributed delays. Phys. Lett. A 2003, 319: 305-316. 10.1016/j.physleta.2003.10.020
Chen A, Huang L, Cao J: Existence and stability of almost periodic solution for BAM neural networks with delays. Appl. Math. Comput. 2003, 137: 177-193. 10.1016/S0096-3003(02)00095-4
Liu B: Global exponential stability for BAM neural networks with time-varying delays in the leakage terms. Nonlinear Anal., Real World Appl. 2013, 14: 559-566. 10.1016/j.nonrwa.2012.07.016
Peng S: Global attractive periodic solutions of BAM neural networks with continuously distributed delays in the leakage terms. Nonlinear Anal., Real World Appl. 2010, 11: 2141-2151. 10.1016/j.nonrwa.2009.06.004
Balasubramaniam P, Kalpana M, Rakkiyappan R: Global asymptotic stability of BAM fuzzy cellular neural networks with time delay in the leakage term, discrete and unbounded distributed delays. Math. Comput. Model. 2011, 53: 839-853. 10.1016/j.mcm.2010.10.021
Lakshmanan S, Park J, Lee T, Jung H, Rakkiyappan R: Stability criteria for BAM neural networks with leakage delays and probabilistic time-varying delays. Appl. Math. Comput. 2013, 219: 9408-9423. 10.1016/j.amc.2013.03.070
Wu Z, Shi P, Su H, Chu J: Sampled-data synchronization of chaotic Lur’e systems with time delays. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24(3):410-421.
Gan Q: Synchronisation of chaotic neural networks with unknown parameters and random time-varying delays based on adaptive sampled-data control and parameter identification. IET Control Theory Appl. 2012, 6(10):1508-1515. 10.1049/iet-cta.2011.0426
Lee T, Park J, Kwon O, Lee S: Stochastic sampled-data control for state estimation of time-varying delayed neural networks. Neural Netw. 2013, 46: 99-108.
Hu J, Li N, Liu X, Zhang G: Sampled-data state estimation for delayed neural networks with Markovian jumping parameters. Nonlinear Dyn. 2013, 73: 275-284. 10.1007/s11071-013-0783-1
Rakkiyappan R, Sakthivel N, Park J, Kwon O: Sampled-data state estimation for Markovian jumping fuzzy cellular neural networks with mode-dependent probabilistic time-varying delays. Appl. Math. Comput. 2013, 221: 741-769.
Fridman E, Blighovsky A: Robust sampled-data control of a class of semilinear parabolic systems. Automatica 2012, 48: 826-836. 10.1016/j.automatica.2012.02.006
Samadi B, Rodrigues L: Stability of sampled-data piecewise affine systems: a time-delay approach. Automatica 2009, 45: 1995-2001. 10.1016/j.automatica.2009.04.025
Rodrigues L: Stability of sampled-data piecewise-affine systems under state feedback. Automatica 2007, 43: 1249-1256. 10.1016/j.automatica.2006.12.016
Zhang C, Jiang L, He Y, Wu H, Wu M: Stability analysis for control systems with aperiodically sampled data using an augmented Lyapunov functional method. IET Control Theory Appl. 2013, 7(9):1219-1226. 10.1049/iet-cta.2012.0814
Seuret A, Peet M: Stability analysis of sampled-data systems using sum of squares. IEEE Trans. Autom. Control 2013, 58(6):1620-1625.
Oishi Y, Fujioka H: Stability and stabilization of aperiodic sampled-data control systems using robust linear matrix inequalities. Automatica 2010, 46: 1327-1333. 10.1016/j.automatica.2010.05.006
Feng L, Song Y: Stability condition for sampled data based control of linear continuous switched systems. Syst. Control Lett. 2011, 60: 787-797. 10.1016/j.sysconle.2011.07.006
Acknowledgements
This work was jointly supported by the National Natural Science Foundation of China under Grant 60875036, the Foundation of Key Laboratory of Advanced Process Control for Light Industry (Jiangnan university), Ministry of Education, P.R. China the Fundamental Research Funds for the Central Universities (JUSRP51317B, JUDCF13042).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
LL carried out the main results of this paper and drafted the manuscript. YY directed the study and helped to inspect the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, L., Yang, Y., Liang, T. et al. The exponential stability of BAM neural networks with leakage time-varying delays and sampled-data state feedback input. Adv Differ Equ 2014, 39 (2014). https://doi.org/10.1186/1687-1847-2014-39
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-39