Abstract
The exponential stability of a class of nonlinear systems by means of alternate control is studied. An exponential stability criterion is given in terms of a set of linear matrix inequalities. Numerical simulations are presented to verify the correction of the obtained results.
Similar content being viewed by others
1 Introduction
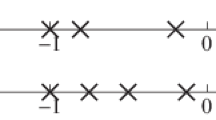
There are many methods to stabilize a nonlinear system. For example, impulsive control methods [1–4], switching control methods [5–9], etc. Intermittent control methods are special cases of switching control methods and have been studied by many researchers, e.g., [10–15]. Within the intermittent control, one adds a continuous control during the first part of the period while in the other part of the period there is no control. This method is available for some cases, but it costs time. For other cases in which the time is very important, this method is not of use. So we advise to add two different controls alternately to the system. We call this system alternate control system. Figure 1 and Figure 2 show the working principles of intermittent control system and alternate control system, from which we conclude that alternate control system is a generalization of intermittent one.
In this paper, we first investigate the stability of the alternate control system, then by using the stability criterion obtained we study the stability of Chua’s oscillator. Also, numerical simulations are illustrated to show the effectiveness of the results.
The rest of the paper is organized as follows. In Section 2, we formulate the problem of alternate control system and introduce some notations and lemmas. We then establish, in Section 3, an exponential stability criterion. In Section 4, we discuss the alternate control of Chua’s oscillator. Lastly, we conclude the paper.
2 Problem formulation and preliminaries
Consider a class of nonlinear systems described by
where presents state vector, is a continuous nonlinear function satisfying and there exists a diagonal matrix such that for any , is constant matrix, denotes the external input of system (1).
For stabilizing the origin of the system (1) by means of a periodically alternate control, we assume that the control imposed on the system is of the following form:
where are constant matrices, denotes the control period, is a constant.
Our target is to design suitable T, τ, , and such that the system (1) can be stabilized at the origin.
By the control law (2), the system (1) can be rewritten as follows:
It is obvious that the system (3) is a classical switched system where the switching rule only depends on the time.
Remark 1 When , the alternate control system (3) becomes the classical intermittent control system [10].
In the sequel, we will use the following two lemmas.
Lemma 1 (Sanchez and Perez [16])
Given any real matrices , , of appropriate dimensions and a scalar such that , the following inequality holds:
Lemma 2 (Boyd et al. [17])
The LMI
where , , and depend affinely on x, is equivalent to
Throughout this paper, we use , , and to denote the transpose, the maximum eigenvalue and the minimum eigenvalue of a square matrix P, respectively. is used to denote the Euclidean norm of the vector x. The matrix norm is also referred to the Euclidean norm. We use (<0, ≤0, ≥0) to denote a symmetrical positive (negative, semi-negative, semi-positive) definite matrix P. is defined by .
3 Main results
Theorem 1 If there exist a symmetric and positive definite matrix , positive scalar constants , , , and scalar constant such that the following hold:
-
(1)
,
-
(2)
,
-
(3)
,
then the origin of the system (3) is exponentially stable, and
where , for any .
Proof Let us construct the following Lyapunov function:
from which we obtain
If , then by (3), (4), and (5) we have
which implies that
Similarly, if , then we have
which implies that
It follows from (7) and (8) that:
(1) If , then we have
So
(2) If , then we have
So
(3) If , then we have
So
(4) If , then we have
So
(5) If , then we have
So
(6) If , then we have
So
By induction, we have:
(7) If , i.e., , then we have
So
(8) If , i.e., , then we have that
From (9) we know that
where .
From (10) we know that
Case 1. If , then
Case 2. If , then
So, for any , we have
where .
It follows from (11) and (12) that, for any ,
By (5), (6), and (13), we conclude that
where , for any .
So we finish the proof. □
From Lemma 2, we know that the two conditions of Theorem 1 are equivalent to the following two LMIs, respectively:
4 Numerical example
The original and dimensionless form of a Chua’s oscillator [18] is given by
where α and β are parameters and is the piecewise linear characteristics of Chua’s diode, which is defined by
where are two constants.
In this section, we set the system parameters as , , , and , which make Chua’s circuit (16) chaotic [18]. Figure 3 shows the chaotic phenomenon of Chua’s oscillator with the initial condition .
We rewrite the system (16) as follows:
where
So
Thus we can choose .
Choosing
With and , solving LMIs (14), (15) and inequality , we obtain a feasible solution:
and
Thus by the previous theorem we see that the origin of the system (3) is exponentially stable. The time response corves of Chua’s oscillator with alternate control is shown in Figure 4.
5 Conclusions
This paper gives a new model of control system, namely alternate control system. A stability criterion is given in terms of linear matrix inequalities. By the new method, the chaotic Chua circuit is controlled.
Obviously, there is no rest time in an alternate control system. By comparing our model with the traditional intermittent control system, we know that our model is a generalization of intermittent control system. The proposed method can be applied to linear and nonlinear systems.
This paper considers systems without delay. For delayed systems [19–21], we know that the methods used to deal with them are different from ones of the systems without delay. We are ready to focus on this aspect in future papers.
Authors’ information
The second author is a Senior Member, IEEE.
References
Yang T: Impulsive Control Theory. Springer, Berlin; 2001.
Yang T: Impulsive control. IEEE Trans. Autom. Control 1999, 44(5):1081-1083. 10.1109/9.763234
Yang T, Chua LO: Impulsive stabilization for control and synchronization of chaotic systems: theory and application to secure communication. IEEE Trans. Circuits Syst. I, Fundam. Theory Appl. 1997, 44(10):976-988. 10.1109/81.633887
Yang Z, Xu D: Stability analysis and design of impulsive control systems with time delay. IEEE Trans. Autom. Control 2007, 52(8):1448-1454.
Allerhand LI, Shaked U: Robust state-dependent switching of linear systems with dwell time. IEEE Trans. Autom. Control 2013, 58(4):994-1001.
Geromel JC, Deaecto GS, Daafouz J: Suboptimal switching control consistency analysis for switched linear systems. IEEE Trans. Autom. Control 2013, 58(7):1857-1861.
Heertjes MF, Sahin IH, van de Wouw N, Heemels WPMH: Switching control in vibration isolation systems. IEEE Trans. Control Syst. Technol. 2013, 21(3):626-635.
Tanwani A, Shim H, Liberzon D: Observability for switched linear systems: characterization and observer design. IEEE Trans. Autom. Control 2013, 58(4):891-904.
Li C, Huang T, Chen G: Exponential stability of time-controlled switching systems with time delay. J. Franklin Inst. 2012, 349(1):216-233. 10.1016/j.jfranklin.2011.10.016
Li C, Feng G, Liao X: Stabilization of nonlinear systems via periodically intermittent control. IEEE Trans. Circuits Syst. II, Express Briefs 2007, 54(11):1019-1023.
Zochowski M: Intermittent dynamical control. Physica D 2000, 145: 181-190. 10.1016/S0167-2789(00)00112-3
Li N, Cao J: Periodically intermittent control on robust exponential synchronization for switched interval coupled networks. Neurocomputing 2014, 131: 52-58.
Huang J, Li C, He X: Stabilization of a memristor-based chaotic system by intermittent control and fuzzy processing. Int. J. Control. Autom. Syst. 2013, 11(3):643-647. 10.1007/s12555-012-9323-x
Huang, J, Li, C, Han, Q: Quasi-synchronization of chaotic neural networks with parameter mismatch by periodically intermittent control. In: Proceeding of CSIE 2009, March 31 - April 2, Los Angeles, California, USA, 7 volumes (2009)
Huang T, Li C, Liu X: Synchronization of chaotic systems with delay using intermittent linear state feedback. Chaos 2008., 18: Article ID 033122
Sanchez EN, Perez JP: Input-to-state stability (ISS) analysis for dynamic NN. IEEE Trans. Circuits Syst. I, Regul. Pap. 1999, 46(11):1395-1398. 10.1109/81.802844
Boyd S, Ghaoui L, Feron EEI, Balakrishnan V: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadephia; 1994.
Shilnikov L: Chau’s circuit: rigorous results and future problems. Int. J. Bifurc. Chaos 1994, 4(3):489-519. 10.1142/S021812749400037X
Xia W, Cao J: Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos 2009., 19(1): Article ID 013120 10.1063/1.3071933
Yang X, Cao J: Stochastic synchronization of coupled neural networks with intermittent control. Phys. Lett. A 2009, 373(36):3259-3272. 10.1016/j.physleta.2009.07.013
Zheng G, Cao J: Robust synchronization of coupled neural networks with mixed delays and uncertain parameters by intermittent pinning control. Neurocomputing 2014, 141: 153-159.
Acknowledgements
This research is supported by the Natural Science Foundation of China (grant No. 61374078), NPRP grant # NPRP 4-1162-1-181 from the Qatar National Research Fund (a member of Qatar Foundation), Scientific & Technological Research Foundation of Chongqing Municipal Education Commission (grant Nos. KJ1401006, KJ1401019), the Fundamental Research Funds for the Central Universities (grant No. XDJK2015D004) and Key Program of Chongqing Three Gorges University (grant No. 14ZD18).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
CL has proposed the ideal of alternate control. YF has proved the main theory and prepared the paper with latex. TH has provided all the figures of the paper. WZ has given some advice to improve the paper. All authors have read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feng, Y., Li, C., Huang, T. et al. Alternate control systems. Adv Differ Equ 2014, 305 (2014). https://doi.org/10.1186/1687-1847-2014-305
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-305