All exact traveling wave solutions of the combined KdV-mKdV equation

Abstract

In this article, we employ the complex method to obtain all meromorphic solutions of complex combined Korteweg-de Vries-modified Korteweg-de Vries equation (KdV-mKdV equation) at first, then we find all exact traveling wave solutions of the combined KdV-mKdV equation. The idea introduced in this paper can be applied to other nonlinear evolution equations. Our results show that all rational and simply periodic exact traveling wave solutions of the combined KdV-mKdV equation are solitary wave solutions, the complex method is simpler than other methods, and there exist some rational solutions $w_{r,2}(z)$ and simply periodic solutions $w_{s,2}(z)$ such that they are not only new but also not degenerated successively by the elliptic function solutions. We believe that this method should play an important role in finding exact solutions in mathematical physics. We also give some computer simulations to illustrate our main results.

MSC: Primary 30D35; secondary 34A05.

PACS Codes: 02.30.Jr; 02.70.Wz; 02.30.-f.

1 Introduction and main results

Studies of various physical structures of nonlinear evolution equations (NLEEqs) have attracted much attention in connection with the important problems that arise in scientific applications. Exact solutions of NLEEqs of mathematical physics have been of significant interest in the literature. Over the last years, much work has been done on the construction of exact solitary wave solutions and periodic wave solutions of nonlinear physical equations. Many methods have been developed by mathematicians and physicists to find special solutions of NLEEqs, such as the inverse scattering method [1], the Darboux transformation method [2], the Hirota bilinear method [3], the Lie group method [4], the bifurcation method of dynamic systems [5–7], the sine-cosine method [8], the tanh-function method [9, 10], the Fan-expansion method [11], and the homogeneous balance method [12]. Practically, there is no unified technique that can be employed to handle all types of nonlinear differential equations. Recently, the complex method was introduced by Yuan et al. [13–15]. It is shown that the complex method provides a powerful mathematical tool for solving a great many nonlinear partial differential equations in mathematical physics.

In 2004, Yu et al. [16] considered the combined KdV-mKdV equation

$$u_t+au{u}_x+b{u}^2{u}_x+\delta u_{xxx},$$

(KdV-mKdV)

where a, b, and δ are constants, the subscripts denote partial derivatives. Making use of the improved trigonometric function method applied to the KdV-mKdV equation, they obtained rich explicit and exact traveling wave solutions, which contain solitary wave solutions, periodic solutions, and combined formal solitary wave solutions.

Yu et al. [16] said that the KdV-mKdV equation is a real physical model concerning many branches in physics. The KdV-mKdV equation may describe the wave propagation of bounded particle with a harmonic force in one-dimensional nonlinear lattice. Particularly, it describes the propagation of ion acoustic waves of small amplitude without Landau damping in plasma physics, and it is also used to explain the propagation of thermal pulse through single crystal of sodium fluoride in solid physics. Up to now, many researches on this equation have been conducted (cf. [17–28]). These authors have found its abundant exact traveling wave solutions including doubly periodic Jacobi elliptic function solutions. In the limit cases, these solutions degenerate to the corresponding solitary wave solutions, shock wave solutions or trigonometric function (singly periodic) solutions.

In order to state our main results, we need some concepts and notations.

A meromorphic function $w(z)$ means that $w(z)$ is holomorphic in the complex plane C except for the poles. α, b, c, $c_i$, and $c_{ij}$ are constants, which may be different from each other in different places. We say that a meromorphic function w belongs to the class W if w is an elliptic function, or a rational function of $e^{\alpha z}$, $\alpha \in \mathbf{C}$, or a rational function of z.

Substituting the traveling wave transformation

$$u(x,t)=w(z),z=kx+\lambda t$$

(TWT)

into the KdV-mKdV equation, and integrating it yields the auxiliary ordinary differential equation

$$\delta k^3{w}^{″}+\lambda w+\frac{ak}{2}{w}^2+\frac{bk}{3}{w}^3+d=0,$$

(1)

where d is an integral constant.

In this article, we employ the complex method to obtain all meromorphic exact solutions of the complex equation (1) first, then combining the transform (TWT) to find all exact traveling wave solutions of the KdV-mKdV equation. The idea introduced in this paper can be applied to other nonlinear evolution equations. Our results show that the complex method is simpler than other methods, and there exist some rational solutions $w_{r,2}(z)$ and simply periodic solutions $w_{s,2}(z)$ which are not only new but also not degenerated successively by the elliptic function solutions. In Section 4, we give some computer simulations to illustrate our main results.

Our main results are Theorems 1 and 2.

Theorem 1 Suppose that $b\delta k\ne 0$, then all meromorphic solutions w of the (1) belong to the class W. Furthermore, (1) has the following three forms of solutions:

• (I) All elliptic function solutions

  $$w_d(z)=\pm \sqrt{-\frac{3\delta k}{2b}}\frac{(-\mathrm{\wp }+C)(4\mathrm{\wp }{C}^2+4{\mathrm{\wp }}^{2}C+2{\mathrm{\wp }}^{\prime }D-\mathrm{\wp }{g}_2-C{g}_2)}{((12C^2-g_2)\mathrm{\wp }+4C^3-3C{g}_2){\mathrm{\wp }}^{\prime }+4D{\mathrm{\wp }}^3+12DC{\mathrm{\wp }}^2-3D{g}_2\mathrm{\wp }-DC{g}_2}-\frac{a}{2b},$$

where $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$, $g_3=0$, $D^2=4C^3-g_{2}C$, $g_2$, and C are arbitrary constants.

• (II) All simply periodic solutions

  $$w_{s,1}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha coth\frac{\alpha }{2}(z-z_0)-\frac{a}{2b}$$

and

$$w_{s,2}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha (coth\frac{\alpha }{2}(z-z_0)-coth\frac{\alpha }{2}(z-z_0-z_1))-\frac{a}{2b}\mp k\sqrt{-\frac{3\delta k}{2b}}\alpha coth\frac{\alpha }{2}{z}_1,$$

where $z_0\in \mathbf{C}$. $4ab=(12b\lambda -a^{2}k-6b\alpha \delta k^4)\sqrt{-\frac{3\delta k}{2b}}$, $k{a}^3+24b^{2}d+6ab\alpha \delta k^4=0$ in the former case, or $z_1\ne 0$, $18k\lambda \delta +4ab\sqrt{-\frac{3\delta k}{2b}}=9{\delta }^2{\alpha }^2{k}^5(\frac{3}{{sinh}^2\frac{\alpha }{2}{z}_1}+1)$, $12bd\sqrt{-\frac{3\delta k}{2b}}=(a\sqrt{-\frac{3\delta k}{2b}}\mp 3\delta k^3\alpha coth\frac{\alpha }{2}{z}_1)(\frac{6\delta k^3{\alpha }^2}{{sinh}^2\frac{\alpha }{2}{z}_1}+\frac{a^2}{2b}\mp a\alpha \sqrt{-\frac{3\delta k}{2b}}coth\frac{\alpha }{2}{z}_1)$ in the latter case.

• (III) All rational function solutions

  $$w_{r,1}(z)=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_0}-\frac{a}{2b}$$

and

$$w_{r,2}(z)=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_0}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_0-z_1}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z_1}-\frac{a}{2b},$$

where $z_0\in \mathbf{C}$. $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$ in the former case, or $a=(3\lambda -\frac{a^{2}k}{4b}-\frac{18\delta k^4}{z_1^2})\sqrt{-\frac{3\delta k}{2b}}$, $(\frac{a^3{k}^3}{8b^2}-\frac{3a\delta k^4}{2b{z}_1^2}-3d)\sqrt{-\frac{3\delta k}{2b}}=\frac{36{\delta }^2{k}^6}{b{z}_1^3}$, $z_1\ne 0$ in the latter case.

Substituting the transform (TWT) into all meromorphic solutions $w(z)$ of (1) gives all exact traveling wave solutions of the KdV-mKdV equations. Therefore, we have Theorem 2.

Theorem 2 Suppose that $b\delta k\ne 0$, then all meromorphic exact traveling wave solutions $w(x,t)$ of the (KdV-mKdV) equation are of the forms below.

• (I) All elliptic function solutions are

  $$w_d(x,t)=w_d(kx+\lambda t),$$

where $3a^2\delta k=36b\lambda \delta +8a{b}^2\sqrt{-\frac{3\delta k}{2b}}$, $3a^3\delta k^2+64b^{3}d=0$, $g_3=0$, $D^2=4C^3-g_{2}C$, $g_2$, and C are arbitrary constants.

• (II) All simply periodic solutions

  $$w_{s,1}(x,t)=w_{s,1}(kx+\lambda t)$$

and

$$w_{s,2}(x,t)=w_{s,2}(kx+\lambda t),$$

where $(x_0,t_0)\in \mathbf{R}\times \mathbf{R}$. $4ab=(12b\lambda -a^{2}k-6b\alpha \delta k^4)\sqrt{-\frac{3\delta k}{2b}}$, $k{a}^3+24b^{2}d+6ab\alpha \delta k^4=0$ in the former case, or $(x_1,t_1)\ne (0,0)$, $18k\lambda \delta +4ab\sqrt{-\frac{3\delta k}{2b}}=9{\delta }^2{\alpha }^2{k}^5(\frac{3}{{sinh}^2\frac{\alpha }{2}(k{x}_1+\lambda t_1)}+1)$, $12bd\sqrt{-\frac{3\delta k}{2b}}=(a\sqrt{-\frac{3\delta k}{2b}}\mp 3\delta k^3\alpha coth\frac{\alpha }{2}(k{x}_1+\lambda t_1))(\frac{6\delta k^3{\alpha }^2}{{sinh}^2\frac{\alpha }{2}(k{x}_1+\lambda t_1)}+\frac{a^2}{2b}\mp a\alpha \sqrt{-\frac{3\delta k}{2b}}coth\frac{\alpha }{2}(k{x}_1+\lambda t_1))$ in the latter case.

• (III) All rational function solutions

  $$w_{r,1}(x,t)=w_{r,1}(kx+\lambda t)$$

and

$$w_{r,2}(x,t)=w_{r,2}(kx+\lambda t),$$

where $(x_0,t_0)\in \mathbf{R}\times \mathbf{R}$. $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$ in the former case, or $a=(3\lambda -\frac{a^{2}k}{4b}-\frac{18\delta k^4}{{(k{x}_1+\lambda t_1)}^2})\sqrt{-\frac{3\delta k}{2b}}$, $(\frac{a^3{k}^3}{8b^2}-\frac{3a\delta k^4}{2b{(k{x}_1+\lambda t_1)}^2}-3d)\sqrt{-\frac{3\delta k}{2b}}=\frac{36{\delta }^2{k}^6}{b{(k{x}_1+\lambda t_1)}^3}$, $(x_1,t_1)\ne (0,0)$ in the latter case.

This paper is organized as follows: In Section 2, the preliminary lemmas and the complex method are given. The proof of Theorem 1 will be given in Section 3. In Section 4, we will give some computer simulations to illustrate our main results. All exact traveling wave solutions of the KdV-mKdV equation are given by Theorem 2. Some conclusions and discussions are given in the final section.

2 Preliminary lemmas and the complex method

In order to give our complex method and the proof of Theorem 1, we need some lemmas and results.

Lemma 1 [29, 30]

Let $k\in \mathbf{N}$, and w be a meromorphic solution of k order, and the Briot-Bouquet equations be

$$F(w^{(k)},w)=\sum _{i=0}^n{P}_i(w){\left(w^{(k)}\right)}^i=0,$$

(2)

where $P_i(w)$ are polynomials with constant coefficients. If w has at least one pole, then w belongs to the class W.

Set $m\in \mathbf{N}:=\{1,2,3,\dots \}$, $r_j\in {\mathbf{N}}_0=\mathbf{N}\cup \{0\}$, $r=(r_0,r_1,\dots ,r_m)$, $j=0,1,\dots ,m$. A differential monomial is defined by

$$M_r[w](z):={[w(z)]}^{r_0}{[w^{\prime }(z)]}^{r_1}{[w^{″}(z)]}^{r_2}\cdots {[w^{(m)}(z)]}^{r_m}.$$

$p(r):=r_0+r_1+\cdots +r_m$ is called the degree of $M_r[w]$. A differential polynomial is defined by

$$P(w,w^{\prime },\dots ,w^{(m)}):=\sum _{r\in I}{a}_r{M}_r[w],$$

where $a_r$ are constants, and I is a finite index set. The total degree of $P(w,w^{\prime },\dots ,w^{(m)})$ is defined by $degP(w,w^{\prime },\dots ,w^{(m)}):={max}_{r\in I}\{p(r)\}$.

We will consider the following complex ordinary differential equations:

$$P(w,w^{\prime },\dots ,w^{(m)})=b{w}^n+c,$$

(3)

where $b\ne 0$, c are constants, $n\in \mathbf{N}$.

Let $p,q\in \mathbf{N}$. Suppose that (3) has a meromorphic solution w with at least one pole, we say that (3) satisfies the weak $〈p,q〉$ condition if on substituting the Laurent series

$$w(z)=\sum _{k=-q}^{\mathrm{\infty }}{c}_k{z}^k,q>0,c_{-q}\ne 0$$

(4)

into (3) we can determine p distinct Laurent singular parts:

$$\sum _{k=-q}^{-1}{c}_k{z}^k.$$

Lemma 2 [15, 31, 32]

Let $p,l,m,n\in \mathbf{N}$, $degF(w^{(m)},w)<n$. Suppose that an m order Briot-Bouquet equation

$$F(w^{(m)},w)=b{w}^n+c$$

(5)

satisfies the weak $〈p,q〉$ condition, then all meromorphic solutions w belong to the class W. If for some values of the parameters such a solution w exists, then the other meromorphic solutions form a one-parametric family $w(z-z_0)$, $z_0\in \mathbf{C}$. Furthermore each elliptic solution with pole at $z=0$ can be written as

$$\begin{array}{rl}w(z)=& \sum _{i=1}^{l-1}\sum _{j=2}^q\frac{{(-1)}^j{c}_{-ij}}{(j-1)!}\frac{d^{j-2}}{d{z}^{j-2}}(\frac{1}{4}{\left[\frac{{\mathrm{\wp }}^{\prime }(z)+B_i}{\mathrm{\wp }(z)-A_i}\right]}^2-\mathrm{\wp }(z))\\ +\sum _{i=1}^{l-1}\frac{c_{-i1}}{2}\frac{{\mathrm{\wp }}^{\prime }(z)+B_i}{\mathrm{\wp }(z)-A_i}+\sum _{j=2}^q\frac{{(-1)}^j{c}_{-lj}}{(j-1)!}\frac{d^{j-2}}{d{z}^{j-2}}\mathrm{\wp }(z)+c_0,\end{array}$$

(6)

where $c_{-ij}$ are given by (4), $B_i^2=4A_i^3-g_2{A}_i-g_3$, and ${\sum }_{i=1}^l{c}_{-i1}=0$.

Each rational function solution $w:=R(z)$ is of the form

$$R(z)=\sum _{i=1}^l\sum _{j=1}^q\frac{c_{ij}}{{(z-z_i)}^j}+c_0,$$

(7)

with l (≤p) distinct poles of multiplicity q.

Each simply periodic solution is a rational function $R(\xi )$ of $\xi =e^{\alpha z}$ ($\alpha \in \mathbf{C}$). $R(\xi )$ has l (≤p) distinct poles of multiplicity q, and is of the form

$$R(\xi )=\sum _{i=1}^l\sum _{j=1}^q\frac{c_{ij}}{{(\xi -{\xi }_i)}^j}+c_0.$$

(8)

In order to give the representations of elliptic solutions, we need some notations and results concerning elliptic functions [31].

Let ${\omega }_1$, ${\omega }_2$ be two given complex numbers such that $Im\frac{{\omega }_1}{{\omega }_2}>0$, $L=L[2{\omega }_1,2{\omega }_2]$ are a discrete subset $L[2{\omega }_1,2{\omega }_2]=\{\omega \mid \omega =2n{\omega }_1+2m{\omega }_2,n,m\in \mathbf{Z}\}$, which is isomorphic to $\mathbf{Z}\times \mathbf{Z}$. The discriminant $\mathrm{\Delta }=\mathrm{\Delta }(c_1,c_2):=c_1^3-27c_2^2$ and

$$s_n=s_n(L):=\sum _{n\ge 3,n\in N}\frac{1}{{\omega }^n}.$$

The Weierstrass elliptic function $\mathrm{\wp }(z):=\mathrm{\wp }(z,g_2,g_3)$ is a meromorphic function with double periods $2{\omega }_1$, $2{\omega }_2$ and satisfies the equation

$${({\mathrm{\wp }}^{\prime }(z))}^2=4\mathrm{\wp }{(z)}^3-g_2\mathrm{\wp }(z)-g_3,$$

(9)

where $g_2=60s_4$, $g_3=140s_6$, and $\mathrm{\Delta }(g_2,g_3)\ne 0$.

If changing (9) to the form

$${({\mathrm{\wp }}^{\prime }(z))}^2=4(\mathrm{\wp }(z)-e_1)(\mathrm{\wp }(z)-e_2)(\mathrm{\wp }(z)-e_3),$$

(10)

we have $e_1=\mathrm{\wp }({\omega }_1)$, $e_2=\mathrm{\wp }({\omega }_2)$, $e_3=\mathrm{\wp }({\omega }_1+{\omega }_2)$.

Inversely, given two complex numbers $g_2$ and $g_3$ such that $\mathrm{\Delta }(g_2,g_3)\ne 0$, then there exists a double period $2{\omega }_1$, $2{\omega }_2$ Weierstrass elliptic function $\mathrm{\wp }(z)$ such that the above relations hold.

Lemma 3 [31, 33]

The Weierstrass elliptic functions $\mathrm{\wp }(z):=\mathrm{\wp }(z,g_2,g_3)$ have two successive degeneracies, and we have the following addition formula.

• (I) Degeneracy to simply periodic functions (i.e., rational functions of one exponential $e^{kz}$) is according to

  $$\mathrm{\wp }(z,3d^2,-d^3)=2d-\frac{3d}{2}{coth}^2\sqrt{\frac{3d}{2}}z,$$

  (11)

if one root $e_j$ is double ($\mathrm{\Delta }(g_2,g_3)=0$).

• (II) Degeneracy to rational functions of z is according to

  $$\mathrm{\wp }(z,0,0)=\frac{1}{z^2}$$

if one root $e_j$ is triple ($g_2=g_3=0$).

• (III) The addition formula is

  $$\mathrm{\wp }(z-z_0)=-\mathrm{\wp }(z)-\mathrm{\wp }(z_0)+\frac{1}{4}{\left[\frac{{\mathrm{\wp }}^{\prime }(z)+{\mathrm{\wp }}^{\prime }(z_0)}{\mathrm{\wp }(z)-\mathrm{\wp }(z_0)}\right]}^2.$$

  (12)

By the above lemmas, we can give a new method below, called the complex method, to find exact solutions of some PDEs.

Step 1. Substituting the transform $T:u(x,t)\to w(z)$, $(x,t)\to z$ into a given PDE gives a nonlinear ordinary differential equations (3) or (5).

Step 2. Substitute (4) into (3) or (5) to determine that the weak $〈p,q〉$ condition holds.

Step 3. By the indeterminate relation (6)-(8) we find the elliptic, rational, and simply periodic solutions $w(z)$ of (3) or (5) with a pole at $z=0$, respectively.

Step 4. By Lemmas 1 and 2 we obtain all meromorphic solutions $w(z-z_0)$.

Step 5. Substituting the inverse transform $T^{-1}$ into these meromorphic solutions $w(z-z_0)$, we get all exact solutions $u(x,t)$ of the originally given PDE.

3 Proof of Theorem 1

Proof of Theorem 1 Substituting (4) into (1) we have $q=1$, $p=2$, $c_{-1}=\pm 2k\sqrt{-\frac{3\delta k}{2b}}$, $c_0=-\frac{a}{2b}$, $c_1=\frac{ak-12\lambda }{24b^2{k}^2}\sqrt{-\frac{2b}{3\delta k}}-\frac{a}{9\delta k^3}$, $c_2$ is an arbitrary constant.

Hence, (1) satisfies the weak $〈2,1〉$ condition and is a second-order Briot-Bouquet differential equation. Obviously, (1) satisfies the dominant condition. So, by Lemma 2, we know that all meromorphic solutions of (1) belong to W. Now we will give the forms of all meromorphic solutions of (1).

By (7), we infer there are indeterminate rational solutions of (1) with a pole at $z=0$:

$$R_1(z)=\frac{c_{12}}{z}+\frac{c_{11}}{z-z_1}+c_{10}.$$

Substituting $R_1(z)$ into (1), we get two distinct forms. One of them is

$$w_{r0,1}(z)=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z}-\frac{a}{2b}.$$

Here $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$. The other is

$$w_{r0,2}(z)=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_1}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z_1}-\frac{a}{2b}.$$

Here $a=(3\lambda -\frac{a^{2}k}{4b}-\frac{18\delta k^4}{z_1^2})\sqrt{-\frac{3\delta k}{2b}}$, $(\frac{a^3{k}^3}{8b^2}-\frac{3a\delta k^4}{2b{z}_1^2}-3d)\sqrt{-\frac{3\delta k}{2b}}=\frac{36{\delta }^2{k}^6}{b{z}_1^3}$.

Thus all rational solutions of (1) are

$$w_{r,1}(z)=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_0}-\frac{a}{2b}$$

and

$$w_{r,2}(z)=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_0}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z-z_0-z_1}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}}{z_1}-\frac{a}{2b},$$

where $z_0\in \mathbf{C}$. $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$ in the former case, or $a=(3\lambda -\frac{a^{2}k}{4b}-\frac{18\delta k^4}{z_1^2})\sqrt{-\frac{3\delta k}{2b}}$, $(\frac{a^3{k}^3}{8b^2}-\frac{3a\delta k^4}{2b{z}_1^2}-3d)\sqrt{-\frac{3\delta k}{2b}}=\frac{36{\delta }^2{k}^6}{b{z}_1^3}$, $z_1\ne 0$ in the latter case.

In order to have simply periodic solutions, set $\xi =exp(\alpha z)$, put $w=R(\xi )$ into (1), then

$$\delta k^3{\alpha }^2[\xi R^{\prime }+{\xi }^2{R}^{″}]+\lambda R+\frac{ak}{2}{R}^2+\frac{bk}{3}{R}^3+d=0.$$

(13)

Substituting

$$R_2(\xi )=\frac{c_{22}}{\xi -1}+\frac{c_{21}}{\xi -{\xi }_1}+c_{20}$$

into (13), we obtain

$$R_{2,1}(\xi )=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}\alpha }{\xi -1}-\frac{a}{2b}\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha$$

and

$$R_{2,2}(\xi )=\pm \frac{2k\sqrt{-\frac{3\delta k}{2b}}\alpha }{\xi -1}\mp \frac{2k\sqrt{-\frac{3\delta k}{2b}}\alpha {\xi }_1}{\xi -{\xi }_1}-\frac{a}{2b}\mp k\frac{\sqrt{-\frac{3\delta k}{2b}}\alpha ({\xi }_1+1)}{{\xi }_1-1},$$

where $4ab=(12b\lambda -a^{2}k-6b\alpha \delta k^4)\sqrt{-\frac{3\delta k}{2b}}$, $k{a}^3+24b^{2}d+6ab\alpha \delta k^4=0$ in the former case, or ${\xi }_1\ne 1$, $-4ab=(\frac{6b\delta k^4{\alpha }^2(1+10{\xi }_1+{\xi }_1^2)}{{({\xi }_1-1)}^2}+a^{2}k-12b\lambda )\sqrt{-\frac{3\delta k}{2b}}$, $-24b^{2}d\sqrt{-\frac{3\delta k}{2b}}=\frac{1}{{({\xi }_1-1)}^3}(a\sqrt{-\frac{3\delta k}{2b}}({\xi }_1-1)\mp 3\delta k^3\alpha ({\xi }_1+1))\times (-48b\delta k^3{\alpha }^2{\xi }_1-a^2{({\xi }_1-1)}^2\pm 2ab\alpha \sqrt{-\frac{3\delta k}{2b}}({\xi }_1^2-1))$ in the latter case.

Substituting $\xi =e^{\alpha z}$ into the above relations, we get simply periodic solutions of (1) with a pole at $z=0$:

$$w_{s0,1}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha coth\frac{\alpha }{2}z-\frac{a}{2b}$$

and

$$w_{s0,2}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha (coth\frac{\alpha }{2}z-coth\frac{\alpha }{2}(z-z_1))-\frac{a}{2b}\mp k\sqrt{-\frac{3\delta k}{2b}}\alpha coth\frac{\alpha }{2}{z}_1,$$

where $4ab=(12b\lambda -a^{2}k-6b\alpha \delta k^4)\sqrt{-\frac{3\delta k}{2b}}$, $k{a}^3+24b^{2}d+6ab\alpha \delta k^4=0$ in the former case, or $z_1\ne 0$, $18k\lambda \delta +4ab\sqrt{-\frac{3\delta k}{2b}}=9{\delta }^2{\alpha }^2{k}^5(\frac{3}{{sinh}^2\frac{\alpha }{2}{z}_1}+1)$, $12bd\sqrt{-\frac{3\delta k}{2b}}=(a\sqrt{-\frac{3\delta k}{2b}}\mp 3\delta k^3\alpha coth\frac{\alpha }{2}{z}_1)(\frac{6\delta k^3{\alpha }^2}{{sinh}^2\frac{\alpha }{2}{z}_1}+\frac{a^2}{2b}\mp a\alpha \sqrt{-\frac{3\delta k}{2b}}coth\frac{\alpha }{2}{z}_1)$ in the latter case.

So all simply periodic solutions of (1) are obtained by

$$w_{s,1}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha coth\frac{\alpha }{2}(z-z_0)-\frac{a}{2b}$$

and

$$w_{s,2}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\alpha (coth\frac{\alpha }{2}(z-z_0)-coth\frac{\alpha }{2}(z-z_0-z_1))-\frac{a}{2b}\mp k\sqrt{-\frac{3\delta k}{2b}}\alpha coth\frac{\alpha }{2}{z}_1,$$

where $z_0\in \mathbf{C}$. $4ab=(12b\lambda -a^{2}k-6b\alpha \delta k^4)\sqrt{-\frac{3\delta k}{2b}}$, $k{a}^3+24b^{2}d+6ab\alpha \delta k^4=0$ in the former case, or $z_1\ne 0$, $18k\lambda \delta +4ab\sqrt{-\frac{3\delta k}{2b}}=9{\delta }^2{\alpha }^2{k}^5(\frac{3}{{sinh}^2\frac{\alpha }{2}{z}_1}+1)$, $12bd\sqrt{-\frac{3\delta k}{2b}}=(a\sqrt{-\frac{3\delta k}{2b}}\mp 3\delta k^3\alpha coth\frac{\alpha }{2}{z}_1)(\frac{6\delta k^3{\alpha }^2}{{sinh}^2\frac{\alpha }{2}{z}_1}+\frac{a^2}{2b}\mp a\alpha \sqrt{-\frac{3\delta k}{2b}}coth\frac{\alpha }{2}{z}_1)$ in the latter case.

Next, we will deduce the forms of all elliptic function solutions of (1).

From (6) in Lemma 2, we have the indeterminate relations of elliptic solutions of (1) with a pole at $z=0$:

$$w_{d0}(z)=\frac{c_{-1}}{2}\frac{{\mathrm{\wp }}^{\prime }(z)+B}{\mathrm{\wp }(z)-A}+c_{30},$$

where $B^2=4A^3-g_{2}A-g_3$. Applying the conclusion II of Lemma 3 to $w_{d0}(z)$, and noting the results of the rational solutions obtained above, we deduce that $c_{30}=-\frac{a}{2b}$, $A=B=0$, $g_3=0$. Then we get

$$w_{d0}(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\frac{{\mathrm{\wp }}^{\prime }(z)}{\mathrm{\wp }(z)}-\frac{a}{2b}.$$

Here $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$, $g_3=0$. Therefore, all elliptic solutions of (1) are of the form

$$w_d(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\frac{{\mathrm{\wp }}^{\prime }(z-z_0)}{\mathrm{\wp }(z-z_0)}-\frac{a}{2b},$$

where $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$, $g_3=0$. Making use of the addition formula of Lemma 3, we rewrite it in the form

$$w_d(z)=\pm k\sqrt{-\frac{3\delta k}{2b}}\frac{(-\mathrm{\wp }+C)(4\mathrm{\wp }{C}^2+4{\mathrm{\wp }}^{2}C+2{\mathrm{\wp }}^{\prime }D-\mathrm{\wp }{g}_2-C{g}_2)}{((12C^2-g_2)\mathrm{\wp }+4C^3-3C{g}_2){\mathrm{\wp }}^{\prime }+4D{\mathrm{\wp }}^3+12DC{\mathrm{\wp }}^2-3D{g}_2\mathrm{\wp }-DC{g}_2}-\frac{a}{2b},$$

where $36b\lambda \delta k^2=(a^3{b}^3-8a{b}^{2}k)\sqrt{-\frac{3\delta k}{2b}}$, $a^3{b}^3=24b^{2}d$, $g_3=0$, $D^2=4C^3-g_{2}C$, $g_2$, and C are arbitrary constants.

The proof of Theorem 1 is complete. □

4 Computer simulations for new solutions

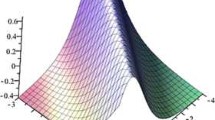
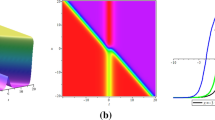
In this section, we give some computer simulations to illustrate our main results. Here we take the new rational solutions $w_{r,2}(z)$ and simply periodic solutions $w_{s,2}(z)$ to further analyze their properties by Figures 1 and 2.

• (1) Take $k=1$, $z_1=1$, $z_0=0$, $\alpha =2$, $d=1$, $\delta =-\frac{1}{6}$, $\lambda =1$; we get from the conditions of $w_{s,2}$ that $a=3.735263299$, $b=0.6826143822$,

• (2) Take $k=1$, $z_1=1$, $z_0=0$, $\alpha =2$, $d=1$, $\delta =-\frac{1}{6}$, $\lambda =1$, we from the conditions of $w_{r,2}$ get $a=1.873178228$, $b=2.241263441$,

Figure 1

The solution of ( KdV-mKdV ) corresponding to ${\mathit{w}}_{\mathit{s}\mathbf{,}\mathbf{2}}$ , (a) $\mathit{t}\mathbf{=}\mathbf{-}\frac{\mathbf{1}}{\mathbf{2}}$ , (b) $\mathit{t}\mathbf{=}\mathbf{0}$ , (c) $\mathit{t}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}$ .

Figure 2

The solution of the KdV-mKdV equation corresponding to ${\mathit{w}}_{\mathit{r}\mathbf{,}\mathbf{2}}$ , (a) $\mathit{t}\mathbf{=}\mathbf{-}\frac{\mathbf{1}}{\mathbf{2}}$ , (b) $\mathit{t}\mathbf{=}\mathbf{0}$ , (c) $\mathit{t}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}$ .

5 Conclusions

The complex method is a very important tool in finding the exact traveling wave solutions of nonlinear evolution equations such as the combined KdV-mKdV equation. In this article, we employ the complex method to obtain all meromorphic solutions of the complex combined KdV-mKdV equation (1) first, then we find all exact traveling wave solutions of the combined KdV-mKdV equation. The idea introduced in this paper can be applied to other nonlinear evolution equations. Our results show that the complex method is simpler than the other methods, and there exist some rational solutions $w_{r,2}(z)$ and simply periodic solutions $w_{s,2}(z)$ such that they are not only new but also not degenerated successively by the elliptic function solutions. Obviously, all rational and simply periodic solutions $w_{r,1}(x,t)$, $w_{r,2}(x,t)$, $w_{s,1}(x,t)$, and $w_{s,2}(x,t)$ are solitary wave solutions. We believe that this method should play an important role in finding exact solutions in mathematical physics.