N-Fold Darboux transformation and solitonic interactions for a Volterra lattice system

Abstract

Under consideration in this paper is a Volterra lattice system. Through symbolic computation, the Lax pair and conservation laws are derived, an integrable lattice hierarchy and an N-fold Darboux transformation (DT) are constructed for this system. Furthermore, N-soliton solutions in terms of determinant are generated with the resulting N-fold DT. Structures of the one-, two- and three-soliton solutions are shown graphically. Overtaking inelastic solitonic interactions between/among the two and three solitons are discussed by figures plotted.

1 Introduction

Explicit solutions of the nonlinear partial differential equations (NPDEs), in particular the soliton solutions, describe certain phenomena (see [1] and references therein). A soliton is a localized nonlinear wave which has particle-like properties [2]. Nonlinear differential-difference equations (NDDEs), taken as spatially discrete analogues of the NPDEs, have received certain attention [2–4]. Studies on the solitons might be divided into two categories, i.e., the continuous and discrete (lattice) cases [2]. Dynamical behaviors of the solitons in the continuous and discrete cases are described by the NPDEs and NDDEs, respectively [2]. NDDEs have some applications in science [2–6]. For example, the Toda lattice [5] is the discrete approximation of the Korteveg-de Vries (KdV) equation in fluids; the discrete nonlinear Schrödinger equation [6] can describe the interaction and propagation of optical pulses in a nonlinear waveguide array; the Volterra lattice system [2, 7–13] is in connection with the spectrum of Langmuir wave in plasma dynamics.

Explicit solutions might be helpful for understanding some processes described by the NDDEs, especially the soliton solutions [2, 14]. Solitons in the discrete systems are sometimes called the lattice solitons [2]. Methods for constructing the explicit solutions of the NDDEs, such as the inverse scattering method [14–16], the Bäcklund transformation [17, 18], the Hirota method [19, 20] and the DT [21–27], have been developed. Among them, the DT is an algebraic one used to obtain the explicit solutions (especially the multi-soliton solutions) in a recursive manner [28]. The key idea of the DT method is to keep the linear eigenvalue problems of the integrable NDDEs invariant.

In this paper, we consider the following Volterra lattice system [2]:

$$M_{n,t}=(1+M_n^2)(M_{n+1}-M_{n-1}),n=0,\pm 1,\pm 2,\dots ,$$

(1)

where $M_n=M(n,t)$ are the functions of the discrete variable n and time variable t, $M_{n,t}=\frac{d{M}_n}{dt}$. Equation (1) is in connection with the spectrum of Langmuir waves in space and laboratory plasmas [2]. References [29–32] have presented some rational, solitary-wave and periodic-wave solutions of (1). In [33], the traveling-wave solution of Volterra lattice was constructed by the optimal homotopy analysis method. Although many people have investigated Eq. (1), to our knowledge, few people have studied Eq. (1) via the N-fold DT. Furthermore, inelastic interaction behaviors of the discrete solitons and conservation laws for this system have not been reported previously.

Different from the previous studies, in this paper, we make further investigation on Eq. (1) via the N-fold DT technique [34]. By employing the AKNS (Ablowitz-Kaup-Newell-Segur) procedure [35], we construct the new Lax pair in matrix form associated with Eq. (1). Based on the derived Lax representation, we directly construct the N-fold Darboux matrices for Eq. (1). Outline of this paper is as follows. In Section 2, an integrable lattice hierarchy associated with Eq. (1) is given from a discrete spectral problem. In Section 3, the Lax pair and N-fold DT of (1) are constructed by employing the AKNS procedure. In Section 4, N-soliton solutions in terms of determinant are derived via the resulting N-fold DT, the solitonic interaction of those solutions is analyzed graphically. In Section 5, conservation laws of (1) are given. Conclusions are made in the last section.

2 An integrable lattice hierarchy associated with Eq. (1)

In this section, we will consider the following discrete spectral problem in the frame of the AKNS system:

$$E{\phi }_n=U_n(u,\lambda ){\phi }_n,U_n(u,\lambda )=\left(\begin{array}{cc}{\lambda }^2& \lambda u_n\\ \lambda v_n& \beta \end{array}\right),$$

(2)

where λ is a spectral parameter and ${\lambda }_t=0$, $\beta \ne 0$ is an arbitrary constant, ${\phi }_n={({\phi }_{1,n},{\phi }_{2,n})}^T$ is a vector eigenfunction, $u={(u_n,v_n)}^T$ is the potential function and E is the shift operator defined by $Ef(n,t)=f(n+1,t)\equiv f_{n+1}$, $E^{-1}f(n,t)=f(n-1,t)\equiv f_{n-1}$, $n\in Z$, $t\in R$, T denoting the transpose of the matrix.

To obtain an integrable lattice hierarchy associated with Eq. (1), according to a scheme for generating the integrable lattice hierarchy [36], we first solve the stationary discrete zero-curvature equation

$$(E{\mathrm{\Gamma }}_1)U_n-U_n{\mathrm{\Gamma }}_1=0,$$

(3)

where ${\mathrm{\Gamma }}_1=\left(\begin{array}{cc}{A}_n& B_n\\ C_n& -A_n\end{array}\right)$. Equation (3) becomes

$$\begin{array}{r}{\lambda }^2{A}_{n+1}-{\lambda }^2{A}_n+\lambda v_n{B}_{n+1}-\lambda u_n{C}_n=0,\\ \lambda u_n{A}_{n+1}+\lambda u_n{A}_n+\beta B_{n+1}-{\lambda }^2{B}_n=0,\\ {\lambda }^2{C}_{n+1}-\lambda v_n{A}_{n+1}-\lambda v_n{A}_n-\beta C_n=0,\\ \lambda u_n{C}_{n+1}-\lambda v_n{B}_n-\beta A_{n+1}+\beta A_n=0.\end{array}$$

(4)

Substituting $A_n={\sum }_{j=0}^{\mathrm{\infty }}{A}_n^{(j)}{\lambda }^{-2j}$ and $B_n={\sum }_{j=0}^{\mathrm{\infty }}{B}_n^{(j)}{\lambda }^{-2j+1}$, $C_n={\sum }_{j=0}^{\mathrm{\infty }}{C}_n^{(j)}{\lambda }^{-2j+1}$ into Eq. (4) leads to the initial relations $B_{n+1}^{(0)}=0$, $C_n^{(0)}=0$ and the recursion relations

$$\begin{array}{r}{A}_{n+1}^{(j)}-A_n^{(j)}+v_n{B}_{n+1}^{(j)}-u_n{C}_n^{(j)}=0,j\ge 0,\\ \beta B_{n+1}^{(j)}-B_n^{(j+1)}+u_n(A_{n+1}^{(j)}+A_n^{(j)})=0,j\ge 0,\\ C_{n+1}^{(j+1)}-\beta C_n^{(j)}-v_n(A_{n+1}^{(j)}+A_n^{(j)})=0,j\ge 0,\\ u_n{C}_{n+1}^{(j+1)}-v_n{B}_n^{(j+1)}-\beta (A_{n+1}^{(j)}-A_n^{(j)})=0,j\ge 0.\end{array}$$

(5)

Now we choose $A_n^{(0)}=-1/2$, and require $A_n^{(j)}{|}_{[u]=0}=0$, $B_n^{(j)}{|}_{[u]=0}=0$, $C_n^{(j)}{|}_{[u]=0}=0$ ($j\ge 1$), the recursion relations (5) determine $A_n^{(j)}$, $B_n^{(j)}$, $C_n^{(j)}$ ($j\ge 1$) uniquely, and the first few coefficients are given as follows:

$$\begin{array}{c}{B}_n^{(1)}=-u_n,C_{n+1}^{(1)}=-v_n,A_n^{(1)}=u_n{v}_{n-1},\hfill \\ B_n^{(2)}=u_n(u_n{v}_{n-1}+u_{n+1}{v}_n)-\beta u_{n+1},\hfill \\ C_{n+1}^{(2)}=v_n(u_n{v}_{n-1}+u_{n+1}{v}_n)-\beta v_{n-1},\dots .\hfill \end{array}$$

Then we define

$${\mathrm{\Gamma }}_1^{(m)}={\lambda }^{2m}{\mathrm{\Gamma }}_1=\left(\begin{array}{cc}{\sum }_{j=0}^m{A}_n^{(j)}{\lambda }^{2m-2j}& {\sum }_{j=0}^m{B}_n^{(j)}{\lambda }^{2m-2j+1}\\ {\sum }_{j=0}^m{C}_n^{(j)}{\lambda }^{2m-2j+1}& -{\sum }_{j=0}^m{A}_n^{(j)}{\lambda }^{2m-2j}\end{array}\right),m\ge 0.$$

(6)

From relations (5), we can derive

$$\left(E{\mathrm{\Gamma }}_1^{(m)}\right)U_n-U_n{\mathrm{\Gamma }}_1^{(m)}=\left(\begin{array}{cc}0& \lambda B_n^{(m+1)}\\ -\lambda C_{n+1}^{(m+1)}& -\beta (A_{n+1}^{(m)}-A_n^{(m)})\end{array}\right).$$

(7)

To present the associated lattice hierarchy, we take a modification

$${\mathrm{\Delta }}_n^{(m)}=\left(\begin{array}{cc}0& 0\\ 0& A_n^{(m)}\end{array}\right),$$

(8)

and define $V_n^{(m)}={\mathrm{\Gamma }}_1^{(m)}+{\mathrm{\Delta }}_n^{(m)}$ for $m\ge 0$. Then we get

$$\left(E{V}_n^{(m)}\right)U_n-U_n{V}_n^{(m)}=\left(\begin{array}{cc}0& \lambda B_n^{(m+1)}-\lambda u_n{A}_n^{(m)}\\ -\lambda C_{n+1}^{(m+1)}+\lambda v_n{A}_{n+1}^{(m)}& 0\end{array}\right).$$

(9)

Let the time evolution of the eigenfunction ${\phi }_n$ of Eq. (2) obey

$${\phi }_{n,t_m}=V_n^{(m)}{\phi }_n,m\ge 0,$$

(10)

and then the compatibility conditions of Eq. (2) and Eq. (10) are $E{\phi }_{n,t_m}=E{({\phi }_n)}_{t_m}$, which are equivalent to

$$U_{n,t_m}=\left(E{V}_n^{(m)}\right)U_n-U_n{V}_n^{(m)},m\ge 0.$$

(11)

Equation (11) gives rise to the following positive hierarchy of lattice equations:

$$\{\begin{array}{l}{u}_{n,t_m}=B_n^{(m+1)}-u_n{A}_n^{(m)},\\ v_{n,t_m}=-C_{n+1}^{(m+1)}+v_n{A}_{n+1}^{(m)}.\end{array}$$

(12)

To obtain the generalized integrable lattice hierarchy associated with Eq. (1), we will further consider the following auxiliary spectral problem:

$${\phi }_{n,t_m}={\mathrm{\Gamma }}_2^{(m)}{\phi }_n,m\ge 0,$$

(13)

where

$${\mathrm{\Gamma }}_2^{(m)}=\left(\begin{array}{cc}{\sum }_{j=0}^m{a}_n^{(j)}{\lambda }^{-2m+2j}& {\sum }_{j=0}^m{b}_n^{(j)}{\lambda }^{-2m+2j-1}\\ {\sum }_{j=0}^m{c}_n^{(j)}{\lambda }^{-2m+2j-1}& -{\sum }_{j=0}^m{a}_n^{(j)}{\lambda }^{-2m+2j}\end{array}\right)+\left(\begin{array}{cc}{a}_n^{(m)}& 0\\ 0& 0\end{array}\right),m\ge 0.$$

(14)

The discrete zero-curvature equations $U_{n,t_m}=(E{\mathrm{\Gamma }}_2^{(m)})U_n-U_n{\mathrm{\Gamma }}_2^{(m)}$ lead to the following negative hierarchy:

$$\{\begin{array}{l}{u}_{n,t_m}=-b_{n+1}^{(m+1)}-u_n{a}_{n+1}^{(m)},\\ v_{n,t_m}=c_n^{(m+1)}+v_n{a}_n^{(m)},\end{array}$$

(15)

with the recursive relations as follows:

$$\begin{array}{c}{a}_n^{(0)}=-1/2,b_n^{(0)}=0,c_{n+1}^{(0)}=0,\hfill \\ b_{n+1}^{(1)}=u_n/\beta ,c_n^{(1)}=v_n/\beta ,a_n^{(1)}=v_n{u}_{n-1}/\beta ,\hfill \\ b_{n+1}^{(2)}=-u_n(u_n{v}_{n-1}+u_{n-1}{v}_n)/{\beta }^2+u_{n-1}/{\beta }^2,\hfill \\ c_n^{(2)}=-v_n(u_n{v}_{n+1}+u_{n-1}{v}_n)/{\beta }^2+v_{n+1}/{\beta }^2,\dots .\hfill \end{array}$$

Let $P_n^{(m)}={\mathrm{\Gamma }}_2^{(m)}-V_n^{(m)}$, we consider the following auxiliary spectral problem:

$${\phi }_{n,t_m}=P_n^{(m)}{\phi }_n,m\ge 0.$$

(16)

The discrete zero-curvature equations lead to the following generalized combined hierarchy:

$$\{\begin{array}{l}{u}_{n,t_m}=-(B_n^{(m+1)}-u_n{A}_n^{(m)})-b_{n+1}^{(m+1)}-u_n{a}_{n+1}^{(m)},\\ v_{n,t_m}=-(-C_{n+1}^{(m+1)}+v_n{A}_{n+1}^{(m)})+c_n^{(m+1)}+v_n{a}_n^{(m)}.\end{array}$$

(17)

When $m=1$, system (17) reduces to

$$\{\begin{array}{l}{u}_{n,t_1}=-u_{n+1}(u_n{v}_n-1)+u_{n-1}(u_n{v}_n-1)/{\beta }^2,\\ v_{n,t_1}=v_{n-1}(u_n{v}_n-1)-v_{n+1}(u_n{v}_n-1)/{\beta }^2.\end{array}$$

(18)

Accordingly, when $m=1$, the time part of the Lax pair of (18) is given as follows:

$$P_n^{(1)}=\left(\begin{array}{cc}1/2{\lambda }^2-1/(2{\lambda }^2)-u_n{v}_{n-1}& \lambda u_n+u_{n-1}/(\beta \lambda )\\ \lambda v_{n-1}+v_n/(\beta \lambda )& -1/2{\lambda }^2+1/(2{\lambda }^2)-v_n{u}_{n-1}/{\beta }^2\end{array}\right).$$

(19)

When $\beta =1$, $u_n=-v_n=-M_n$, system (18) reduces to Eq. (1).

The Hamiltonian structure often guarantees the existence of infinitely many symmetries and infinitely many conserved functionals, exhibiting integrability of the equations under consideration [37]. For the obtained lattice hierarchies (12), (15) and (17), we also may construct their Hamiltonian structures. The aim of this paper is to construct N-fold DT and multi-soliton solutions in terms of determinant of Eq. (1). Hence, as to the detailed derivation process on how to construct Hamiltonian structures of the obtained hierarchies, we refer the reader to the work of Ma [37], here we omit them for simplification.

3 N-Fold DT of Eq. (1)

At present, more research on the Lax integrable NPDEs has been done via the N-fold DT [38–41], for the Lax integrable NDDEs, more research has been done by a single DT (i.e., 1-fold DT) [21–27]. However, as far as we know, few studies on the NDDEs have been done by constructing the N-fold DT. Although the N-fold DT can be interpreted as a superposition of the 1-fold DT, comparing with the 1-fold DT, the biggest advantage of N-fold DT is that we can obtain the relationships between the new multi-soliton solutions and the seed solutions without complicated iterations, so it is meaningful to generalize the N-fold DT technique from NPDEs to NDDEs.

With the aid of symbolic computation Maple, we can construct the Lax pair for (1) as follows:

$$E{\phi }_n=U_n{\phi }_n=\left(\begin{array}{cc}{\lambda }^2& -\lambda M_n\\ \lambda M_n& 1\end{array}\right){\phi }_n,$$

(20)

$${\phi }_{n,t}=V_n{\phi }_n=\left(\begin{array}{cc}\frac{{\lambda }^2}{2}-\frac{1}{2{\lambda }^2}+M_n{M}_{n-1}& -\lambda M_n-\frac{M_{n-1}}{\lambda }\\ \lambda M_{n-1}+\frac{M_n}{\lambda }& -\frac{{\lambda }^2}{2}+\frac{1}{2{\lambda }^2}+M_n{M}_{n-1}\end{array}\right){\phi }_n.$$

(21)

The integrability condition between (20) and (21) gives rise to (1). In what follows, we proceed to establish the DT of (1). In essence, the DT is a special gauge transformation of the solutions for (20) and (21). We introduce the following gauge transformation:

$${\tilde{\phi }}_n=T_n{\phi }_n,$$

(22)

where ${\tilde{\phi }}_n$ is required to satisfy (20) and (21) with $U_n$ and $V_n$ replaced respectively by ${\tilde{U}}_n$ and ${\tilde{V}}_n$, i.e.,

$${\tilde{\phi }}_n={\tilde{U}}_n{\tilde{\phi }}_n,{\tilde{U}}_n=T_{n+1}{U}_n{T_n}^{-1},$$

(23)

$${\tilde{\phi }}_{n,t}={\tilde{V}}_n{\tilde{\phi }}_n,{\tilde{V}}_n=(T_{n,t}+T_n{V}_n){T_n}^{-1}.$$

(24)

${\tilde{U}}_n$ and ${\tilde{V}}_n$ have the same forms as $U_n$ and $V_n$, respectively, except replacing $M_n$ with ${\tilde{M}}_n$, then we can obtain a new solution ${\tilde{M}}_n$ from the old one $M_n$ of (1). It is obvious that the Darboux matrix $T_n$ is a key step for constructing the DT, a proper $T_n$ will ensure the correctness of the N-fold DT of (1). Hereby, we construct a special $T_n$ as follows:

$$T_n=\left(\begin{array}{cc}{a}_n& b_n\\ c_n& d_n\end{array}\right)=\left(\begin{array}{cc}{\lambda }^{2N+1}+{\sum }_{j=-N-1}^{N-1}{a}_n^{(2j+1)}{\lambda }^{2j+1}& {\sum }_{j=-N}^N{b}_n^{(2j)}{\lambda }^{2j}\\ -{\sum }_{j=-N}^N{b}_n^{(-2j)}{\lambda }^{2j}& {\lambda }^{-2N-1}+{\sum }_{j=-N}^N{a}_n^{(-2j-1)}{\lambda }^{2j+1}\end{array}\right),$$

(25)

where $a_n^{(j)}$, $b_n^{(j)}$ are the functions of n and t. $a_n^{(j)}$, $b_n^{(j)}$ can be determined by the following linear algebraic system:

$$\begin{array}{r}\sum _{j=-N-1}^{N-1}{a}_n^{(2j+1)}{\lambda }_i^{2j+1}+\sum _{j=-N}^N{b}_n^{(2j)}{\lambda }_i^{2j}{\delta }_{i,n}=-{\lambda }_i^{2N+1},\\ -\sum _{j=-N}^N{b}_n^{(-2j)}{\lambda }_i^{2j}+\sum _{j=-N}^N{a}_n^{(-2j-1)}{\lambda }_i^{2j+1}{\delta }_{i,n}=-{\lambda }_i^{-2N-1}{\delta }_{i,n},\end{array}$$

(26)

where

$${\delta }_{i,n}=\frac{{\phi }_{2,n}({\lambda }_i)}{{\phi }_{1,n}({\lambda }_i)},1\le i\le 2N+1,$$

(27)

and ${\phi }_n=({\phi }_{1,n},{\phi }_{2,n})$ is a solution of (20) and (21). When the $2N+1$ parameters ${\lambda }_i$ (${\lambda }_i\ne {\lambda }_j$, $i\ne j$) are suitably chosen so that the determinant of the coefficients for (26) is nonzero, the transformation $T_n$ is determined by (26) uniquely.

Equation (25) shows that ${\lambda }^{4N+2}det{T}_n$ is the $(8N+4)$th order polynomial of λ and

$$det{T}_n({\lambda }_i)=a_n({\lambda }_i)d_n({\lambda }_i)-b_n({\lambda }_i)c_n({\lambda }_i),$$

(28)

from (22), (25) and (26), we have

$$a_n({\lambda }_i)=-b_n({\lambda }_i){\delta }_{i,n},c_n({\lambda }_i)=-d_n({\lambda }_i){\delta }_{i,n}.$$

(29)

So we determine that

$$det{T}_n({\lambda }_i)=0,$$

(30)

which means that ${\lambda }_i$ (${\lambda }_i\ne 0$) ($i=1,2,\dots ,2N+1$) are the roots of the ${\lambda }^{4N+2}det{T}_n$, i.e.,

$$det{T}_n={\lambda }^{-4N-2}{a}_n^{(-2N-1)}\prod _{i=1}^{2N+1}{({\lambda }^2-{\lambda }_i^2)}^2.$$

(31)

By using the above facts, we can prove the following theorem.

Theorem 1 Matrices ${\tilde{U}}_n$ and ${\tilde{V}}_n$ determined by (23) and (24) have the same forms as $U_n$ and $V_n$ respectively, where the transformation from the old potential $M_n$ into the new one ${\tilde{M}}_n$ is given by

$${\tilde{M}}_n=M_n{a}_{n+1}^{(-2N-1)}-b_{n+1}^{(-2N)}.$$

(32)

The proof of the form invariance for ${\tilde{U}}_n$, ${\tilde{V}}_n$ and $U_n$, $V_n$ can refer to the context in [34], the proof process is similar (for proof details, see the Appendix). According to Theorem 1, the transformations (22) and (32) can change the Lax pair (20) and (21) into the Lax pair of the same type (23) and (24). Therefore, both of Lax pairs lead to (1). Transformations (22) and (32) are called an N-DT of (1).

4 N-Soliton solutions and inelastic interaction of Eq. (1)

In the following, we will give some explicit solutions of (1) via transformations (22) and (32). Substituting a trivial solution $M_n=0$ into (20) and (21), we can give one solution of the Lax pair (20) and (21) with $\lambda ={\lambda }_i$ ($i=1,2,\dots ,2N+1$) as follows:

$$\varphi =\left(\begin{array}{c}{\lambda }_i^{2n}{e}^{[{\lambda }_i^2/2-1/(2{\lambda }_i^2)]t}\\ e^{-[{\lambda }_i^2/2-1/(2{\lambda }_i^2)]t}\end{array}\right).$$

(33)

According to (27), we have

$${\delta }_{i,n}=\frac{1}{{\lambda }_i^{2n}}{e}^{(1/{\lambda }_i^2-{\lambda }_i^2)t},{\delta }_{i,n+1}=\frac{{\delta }_{i,n}}{{\lambda }_i^2}.$$

(34)

Solving the linear algebraic system (26) by use of Cramer’s rule leads to

$$a_n^{(-2N-1)}=\frac{\mathrm{\Delta }{a}_n^{(-2N-1)}}{\mathrm{\Delta }},b_n^{(-2N)}=\frac{\mathrm{\Delta }{b}_n^{(-2N)}}{\mathrm{\Delta }},$$

(35)

with

$$\mathrm{\Delta }=\left|\begin{array}{cccccc}{\lambda }_1^{2N-1}& \cdots & {\lambda }_1^{-2N-1}& {\lambda }_1^{-2N}{\delta }_{1,n}& \cdots & {\lambda }_1^{2N}{\delta }_{1,n}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ {\lambda }_{2N+1}^{2N-1}& \cdots & {\lambda }_{2N+1}^{-2N-1}& {\lambda }_{2N+1}^{-2N}{\delta }_{2N+1,n}& \cdots & {\lambda }_{2N+1}^{2N}{\delta }_{2N+1,n}\\ {\lambda }_1^{-2N+1}{\delta }_{1,n}& \cdots & {\lambda }_1^{2N+1}{\delta }_{1,n}& -{\lambda }_1^{2N}& \cdots & -{\lambda }_1^{-2N}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ {\lambda }_{2N+1}^{-2N+1}{\delta }_{2N+1,n}& \cdots & {\lambda }_{2N+1}^{2N+1}{\delta }_{2N+1,n}& -{\lambda }_{2N+1}^{2N}& \cdots & -{\lambda }_{2N+1}^{-2N}\end{array}\right|,$$

and $\mathrm{\Delta }{a}_n^{(-2N-1)}$ is produced from Δ by replacing its $(2N+1)$th column with ${(-{\lambda }_1^{2N+1},\dots ,-{\lambda }_{2N+1}^{2N+1},-{\lambda }_1^{-2N-1}{\delta }_{1,n},\dots ,-{\lambda }_{2N+1}^{-2N-1}{\delta }_{2N+1,n})}^T$, $\mathrm{\Delta }{b}_n^{(-2N)}$ is produced from Δ by replacing its $(4N+2)$th column with ${(-{\lambda }_1^{2N+1},\dots ,-{\lambda }_{2N+1}^{2N+1},-{\lambda }_1^{-2N-1}{\delta }_{1,n},\dots ,-{\lambda }_{2N+1}^{-2N-1}{\delta }_{2N+1,n})}^T$.

By use of (32) and (34), we derive a new solution as follows:

$${\tilde{M}}_n=-b_{n+1}^{(-2N)}.$$

(36)

From (35), we can see that solution (36) is a solution in terms of determinants [38, 39]. Here we obtain the solutions in determinant form of NDDEs. However, in [42], a set of coupled conditions consisting of NDDEs is presented for Casorati determinants to solve the Toda lattice equation. The resulting set of eigenfunctions leads to complexitons through the Casoratian formulation, a feasible way has been presented to construct a broad class of Casorati determinant solutions including complexitons and generalized Casorati determinant solutions of the Toda lattice equation. Ma and a co-worker [42] also indicate that integrable equations can have three different kinds of explicit exact transcendental function solutions: negatons, positons and complexitons. Solitons are usually a specific class of negatons. Roughly speaking, negatons and positons are solutions which involve exponential functions and trigonometric functions of space variables, respectively, and they are all associated with real eigenvalues of the associated spectral problems. But complexitons are different solutions which involve both exponential and trigonometric functions of space variables, and they are associated with complex eigenvalues of the associated spectral problems [42]. It is worth pointing out that our results seem to be different from those reported in [42] considering determinant form, but Ma and a co-worker [42] pointed out that the Casorati determinant solution has actually resulted from the Darboux transformation of the Toda lattice equation. Hence we think that these solutions may be the same as Casorati determinant solutions in essence, they may be different only in form, of course, the relation between two kinds of determinant solutions is worthwhile to be studied further. However, we should point out that there are some differences between our method and [42]. Firstly, the Lax pairs are different, one is the matrix form, the other is the operator form; secondly, the deducing steps are different, comparing with [42] we directly construct the Darboux matrix $T_n$, let a Lax pair be covariant with respect to the action of the DT; thirdly, our results and Casorati determinant solutions have different forms. For our results, when choosing different λ, whether we can get the negatons, positons and complexitons may need further investigation. In what follows, we mainly consider multi-soliton solutions and the solitonic interaction of Eq. (1), this is the topic that we would like to address in this paper.

To understand solution (36), when $N=0$ and $N=1$, we plot their structure figures as shown in Figures 1 to 3.

Figure 1

Evolution plots of solution ( 38 ) with the parameters chosen as (a) ${\mathit{\lambda }}_{\mathbf{1}}\mathbf{=}\mathbf{0.8}$ , (b) ${\mathit{\lambda }}_{\mathbf{1}}\mathbf{=}\mathbf{1.2}$ at different time.

• (I) When $N=0$, let $\lambda ={\lambda }_1$. Solving the linear algebraic system (26) leads to

  $$a_n^{(-1)}=\frac{\mathrm{\Delta }{a}_n^{(-1)}}{\mathrm{\Delta }},b_n^{(0)}=\frac{\mathrm{\Delta }{b}_n^{(0)}}{\mathrm{\Delta }},$$

  (37)

with

$$\mathrm{\Delta }=\left|\begin{array}{cc}\frac{1}{{\lambda }_1}& {\delta }_{1,n}\\ {\lambda }_1{\delta }_{1,n}& -1\end{array}\right|,\mathrm{\Delta }{a}_n^{(-1)}=\left|\begin{array}{cc}-{\lambda }_1& {\delta }_{1,n}\\ -\frac{{\delta }_{1,n}}{{\lambda }_1}& -1\end{array}\right|,\mathrm{\Delta }{b}_n^{(0)}=\left|\begin{array}{cc}\frac{1}{{\lambda }_1}& -{\lambda }_1\\ {\lambda }_1{\delta }_{1,n}& -\frac{{\delta }_{1,n}}{{\lambda }_1}\end{array}\right|.$$

Therefore, an explicit solution of (1) is obtained as follows:

$${\tilde{M}}_n=-b_{n+1}^{(0)}.$$

(38)

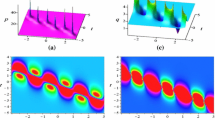
To understand solution (38), we plot its structure figures as shown in Figure 1, it is one-soliton solution. Figure 1 shows the anti-bell-shape soliton and bell-shape soliton for (38), and solution (38) is the anti-bell soliton when $0<{\lambda }_1<1$, while bell soliton structure when ${\lambda }_1>1$. When ${\lambda }_1<0$, solution (38) is a complex solution, whose imaginary and real parts are both periodic wave structures (here we omit their plots).

• (II) When $N=1$, let $\lambda ={\lambda }_i$ ($i=1,2,3$). Solving the linear algebraic system (26) leads to

  $$a_n^{(-3)}=\frac{\mathrm{\Delta }{a}_n^{(-3)}}{\mathrm{\Delta }},b_n^{(-2)}=\frac{\mathrm{\Delta }{b}_n^{(-2)}}{\mathrm{\Delta }},$$

  (39)

with

$$\begin{array}{c}\mathrm{\Delta }=\left|\begin{array}{cccccc}{\lambda }_1& \frac{1}{{\lambda }_1}& \frac{1}{{\lambda }_1^3}& \frac{{\delta }_{1,n}}{{\lambda }_1^2}& {\delta }_{1,n}& {\lambda }_1^2{\delta }_{1,n}\\ {\lambda }_2& \frac{1}{{\lambda }_2}& \frac{1}{{\lambda }_2^3}& \frac{{\delta }_{2,n}}{{\lambda }_2^2}& {\delta }_{2,n}& {\lambda }_2^2{\delta }_{2,n}\\ {\lambda }_3& \frac{1}{{\lambda }_3}& \frac{1}{{\lambda }_3^3}& \frac{{\delta }_{3,n}}{{\lambda }_3^2}& {\delta }_{3,n}& {\lambda }_3^2{\delta }_{3,n}\\ \frac{{\delta }_{1,n}}{{\lambda }_1}& {\lambda }_1{\delta }_{1,n}& {\lambda }_1^3{\delta }_{4,n}& -{\lambda }_1^2& -1& -\frac{1}{{\lambda }_1^2}\\ \frac{{\delta }_{2,n}}{{\lambda }_2}& {\lambda }_2{\delta }_{2,n}& {\lambda }_2^3{\delta }_{3,n}& -{\lambda }_2^2& -1& -\frac{1}{{\lambda }_2^2}\\ \frac{{\delta }_{3,n}}{{\lambda }_3}& {\lambda }_3{\delta }_{3,n}& {\lambda }_3^3{\delta }_{3,n}& -{\lambda }_3^2& -1& -\frac{1}{{\lambda }_3^2}\end{array}\right|,\hfill \\ \mathrm{\Delta }{a}_n^{(-3)}=\left|\begin{array}{cccccc}{\lambda }_1& \frac{1}{{\lambda }_1}& -{\lambda }_1^3& \frac{{\delta }_{1,n}}{{\lambda }_1^2}& {\delta }_{1,n}& {\lambda }_1^2{\delta }_{1,n}\\ {\lambda }_2& \frac{1}{{\lambda }_2}& -{\lambda }_2^3& \frac{{\delta }_{2,n}}{{\lambda }_2^2}& {\delta }_{2,n}& {\lambda }_2^2{\delta }_{2,n}\\ {\lambda }_3& \frac{1}{{\lambda }_3}& -{\lambda }_3^3& \frac{{\delta }_{3,n}}{{\lambda }_3^2}& {\delta }_{3,n}& {\lambda }_3^2{\delta }_{3,n}\\ \frac{{\delta }_{1,n}}{{\lambda }_1}& {\lambda }_1{\delta }_{1,n}& -\frac{{\delta }_{1,n}}{{\lambda }_1^3}& -{\lambda }_1^2& -1& -\frac{1}{{\lambda }_1^2}\\ \frac{{\delta }_{2,n}}{{\lambda }_2}& {\lambda }_2{\delta }_{2,n}& -\frac{{\delta }_{2,n}}{{\lambda }_2^3}& -{\lambda }_2^2& -1& -\frac{1}{{\lambda }_2^2}\\ \frac{{\delta }_{3,n}}{{\lambda }_3}& {\lambda }_3{\delta }_{3,n}& -\frac{{\delta }_{3,n}}{{\lambda }_3^3}& -{\lambda }_3^2& -1& -\frac{1}{{\lambda }_3^2}\end{array}\right|,\hfill \\ \mathrm{\Delta }{b}_n^{(-2)}=\left|\begin{array}{cccccc}{\lambda }_1& \frac{1}{{\lambda }_1}& \frac{1}{{\lambda }_1^3}& \frac{{\delta }_{1,n}}{{\lambda }_1^2}& {\delta }_{1,n}& -{\lambda }_1^3\\ {\lambda }_2& \frac{1}{{\lambda }_2}& \frac{1}{{\lambda }_2^3}& \frac{{\delta }_{2,n}}{{\lambda }_2^2}& {\delta }_{2,n}& -{\lambda }_2^3\\ {\lambda }_3& \frac{1}{{\lambda }_3}& \frac{1}{{\lambda }_3^3}& \frac{{\delta }_{3,n}}{{\lambda }_3^2}& {\delta }_{3,n}& -{\lambda }_3^3\\ \frac{{\delta }_{1,n}}{{\lambda }_1}& {\lambda }_1{\delta }_{1,n}& {\lambda }_1^3{\delta }_{4,n}& -{\lambda }_1^2& -1& -\frac{{\delta }_{1,n}}{{\lambda }_1^3}\\ \frac{{\delta }_{2,n}}{{\lambda }_2}& {\lambda }_2{\delta }_{2,n}& {\lambda }_2^3{\delta }_{3,n}& -{\lambda }_2^2& -1& -\frac{{\delta }_{2,n}}{{\lambda }_2^3}\\ \frac{{\delta }_{3,n}}{{\lambda }_3}& {\lambda }_3{\delta }_{3,n}& {\lambda }_3^3{\delta }_{3,n}& -{\lambda }_3^2& -1& -\frac{{\delta }_{3,n}}{{\lambda }_3^3}\end{array}\right|.\hfill \end{array}$$

Therefore, another explicit solution of (1) is obtained as follows:

$${\tilde{M}}_n=-b_{n+1}^{(-2)}.$$

(40)

When $N=1$ and the parameters are suitably chosen, solution (40) is the two-soliton and three-soliton solution, respectively, the corresponding evolution plots are shown in Figures 2 to 3. Figure 2 shows the overtaking collision interactions between two solitons with a bell-shaped and an anti-bell-shaped soliton with different amplitudes along the same propagation direction for solution (40) at different time. The bell-shaped soliton with higher amplitude travels faster than the anti-bell-shaped soliton with lower amplitude. After the overtaking interaction, the amplitude of the anti-bell-shaped soliton becomes higher; however, the amplitude of the bell-shaped soliton becomes lower. The final two solitons move along the same direction and preserve their shapes and amplitudes, from which we can find that the solitonic shapes and amplitudes have changed after the interaction, the interactions between two solitons are inelastic. Figure 3 displays the overtaking collision interactions among three solitons with two bell-shaped solitons and an anti-bell-shaped soliton with different amplitudes along the same propagation direction of solution (40) at different time, the solitons with higher amplitude travel faster than those with lower amplitudes. After the overtaking interaction, the amplitude of the higher bell-shaped soliton becomes lowest; however, the amplitudes of the other two become higher, and the lower solitons travel faster than those with higher amplitudes after the interaction. The final three solitons move along the same direction and preserve their shapes, amplitudes and velocities. The solitonic shapes and amplitudes have changed after the interaction, so that the solitonic interactions among three solitons are also inelastic. As we know, the inelastic interaction phenomenon is new for (1).

Figure 2

Evolution plots of two-soliton solutions with overtaking collision behavior via ( 40 ) with the parameters ${\mathit{\lambda }}_{\mathbf{1}}\mathbf{=}\mathbf{1.0}$ , ${\mathit{\lambda }}_{\mathbf{2}}\mathbf{=}\mathbf{1.4}$ , ${\mathit{\lambda }}_{\mathbf{3}}\mathbf{=}\mathbf{1.6}$ at different time.

Figure 3

Evolution plots of three-soliton solutions with overtaking collision behavior via ( 40 ) with the parameters ${\mathit{\lambda }}_{\mathbf{1}}\mathbf{=}\mathbf{1.2}$ , ${\mathit{\lambda }}_{\mathbf{2}}\mathbf{=}\mathbf{1.4}$ , ${\mathit{\lambda }}_{\mathbf{3}}\mathbf{=}\mathbf{1.6}$ at different time.

With symbolic computation, solution (36) with $N=0$ and $N=1$ has been verified by substituting them into (1). When solution (36) is the soliton solution, note that solution (36) is the $(2N+1)$-soliton solution if ${\lambda }_i\ne 1$ and ${\lambda }_i\ne {\lambda }_j$ ($i,j=1,2,\dots ,2N+1$). However, the corresponding $(2N+1)$-soliton solution will reduce to the $(2N)$-soliton solution when one of ${\lambda }_i^{\prime }s$ ($i=1,2,\dots ,2N+1$, $N\ge 1$) is 1, which can be seen from Figures 2 to 3. The $(2N)$-soliton and $(2N+1)$-soliton solutions can make up the N-soliton solution of (1).

In [34], the elastic interaction of the solitons for a discrete system has been discussed. In this paper, we have found the inelastic interaction of the solitons in the discrete system. Therefore, we can conclude that, similar to the continuous systems, there exist the elastic interaction and inelastic interaction in the discrete systems.

5 Conservation laws of Eq. (1)

Conservation laws play a role in discussing the integrability for the NDDEs [34, 43], and the first three conservation laws describe the energy, momentum and Hamiltonian conservation laws, respectively. In the following, we will derive infinitely many conservation laws for (1).

From (20) and (21), we can get

$${\phi }_{1,n+1}={\lambda }^2{\phi }_{1,n}-\lambda M_n{\phi }_{2,n},{\phi }_{2,n+1}=\lambda M_n{\phi }_{1,n}-\lambda {\phi }_{2,n}$$

(41)

and

$$\frac{{\phi }_{1,n+1}}{{\phi }_{1,n}}={\lambda }^2-\lambda M_n{\theta }_n,\frac{{\phi }_{2,n+1}}{{\phi }_{2,n}}=\frac{\lambda M_n}{{\theta }_n}+1,$$

(42)

where ${\theta }_n={\phi }_{2,n}/{\phi }_{1,n}$. From (42), we can get

$${\lambda }^2{\theta }_{n+1}-\lambda {\theta }_n{\theta }_{n+1}-\lambda M_n-{\theta }_n=0.$$

(43)

Assume that

$${\theta }_n=\sum _{j=1}^{\mathrm{\infty }}\frac{{{\theta }_n}^{(j)}}{{\lambda }^j}.$$

(44)

Substituting (44) into (43), we obtain the following recursion relation:

$${{\theta }_n}^{(1)}=M_{n-1},{{\theta }_n}^{(2)}=0,{{\theta }_n}^{(m+2)}=M_n\sum _{j=1}^m{{\theta }_n}^{(j)}{{\theta }_n}^{(m+1-j)}-{{\theta }_n}^{(m)}(m\ge 0).$$

(45)

From (21) and (42), direct calculation leads to

$${[ln({\lambda }^2-\lambda M_n{\theta }_n)]}_t=(E-1)[{\lambda }^2+M_n{M}_{n-1}-(\lambda M_n+\frac{M_{n-1}}{\lambda }){\theta }_n].$$

(46)

Equating the same powers of λ in (46), we can get an infinite number of conservation laws for (1). The first two conservation laws are listed as follows:

$${(M_n{M}_{n-1})}_t=(E-1)[M_n{M}_{n-2}(1+{M_{n-1}}^2)-{M_{n-1}}^2],$$

(47)

$$\begin{array}{c}{[M_{n-2}+(M_{n-2}+\frac{1}{2}){M_{n-1}}^2]}_t\hfill \\ =(E-1)[(M_n{M}_{n-1}{M_{n-2}}^2+M_{n-1}{M}_{n-2})(1+{M_{n-1}}^2)\hfill \\ +(M_n{M}_{n-3}+M_{n-1}{M}_{n-3})(1+{M_{n-2}}^2)].\hfill \end{array}$$

(48)

6 Conclusions

In this paper, an integrable lattice hierarchy and N-fold DT (22) and (32) for (1) have been constructed based on its discrete spectral problem. We have derived N-soliton solutions (36) in terms of determinant via the resulting DT. Based on the solutions obtained, one- two- and three-solitonic structures are shown graphically: Figure 1 exhibits the one-soliton structure with $N=0$; Figures 2 and 3 show the overtaking inelastic solitonic interactions between/among the two and three solitons with $N=1$. Solitonic shapes and amplitudes have changed after the interaction. When solution (36) is solitonic, it is worth pointing out that solution (36) is the $(2N+1)$-soliton solution if ${\lambda }_i\ne 1$ and ${\lambda }_i\ne {\lambda }_j$ ($i,j=1,2,\dots ,2N+1$); and further, the corresponding $(2N+1)$-soliton solutions can reduce to the $(2N)$-soliton solutions if one of ${\lambda }_i$’s ($i=1,2,\dots ,2N+1$, $N\ge 1$) is 1. Conservation laws (47) and (48) for (1) have been explicitly given.

Appendix

Proof of Theorem 1 Let $T_n^{-1}=T_n^{\ast }/det{T}_n$ and

$$F(\lambda )=T_{n+1}U{T_n}^{\ast }=\left(\begin{array}{cc}{f}_{11}(\lambda ,n)& f_{12}(\lambda ,n)\\ f_{21}(\lambda ,n)& f_{22}(\lambda ,n)\end{array}\right).$$

(49)

It can be verified that ${\lambda }^{4N+2}{f}_{11}(\lambda ,n)$ is $(8N+6)$th order polynomial in λ, ${\lambda }^{4N+2}{f}_{12}(\lambda ,n)$ and ${\lambda }^{4N+2}{f}_{21}(\lambda ,n)$ are $(8N+5)$th order polynomials in λ, and ${\lambda }^{4N+2}{f}_{22}(\lambda ,n)$ is $(8N+4)$th order polynomial in λ.

From (20) and (25), we have

$$a_n(\lambda )=-{\delta }_{i,n}{b}_n(\lambda ),c_n(\lambda )=-{\delta }_{i,n}{d}_n(\lambda ),{\delta }_{i,n+1}=\frac{{\lambda }_i{M}_n+{\delta }_{i,n}}{{\lambda }_i^2-{\lambda }_i{M}_n{\delta }_{i,n}}.$$

(50)

Moreover, we can prove that $f_{11}({\lambda }_i,n)$, $f_{12}({\lambda }_i,n)$, $f_{21}({\lambda }_i,n)$ and $f_{22}({\lambda }_i,n)$ are all zeroes (the detailed proof is omitted). So we have

$$T_{n+1}U{T_n}^{\ast }=det{T}_n\cdot P_n,$$

(51)

with

$$P_n=\left(\begin{array}{cc}{P_{11}}^{(2)}{\lambda }^2+{P_{11}}^{(1)}\lambda +{P_{11}}^{(0)}& {P_{12}}^{(1)}\lambda +{P_{12}}^{(0)}\\ {P_{21}}^{(1)}\lambda +{P_{21}}^{(0)}& {P_{22}}^{(0)}\end{array}\right).$$

(52)

Thus we obtain

$$T_{n+1}U=P_n{T}_n.$$

(53)

Using (32) and comparing the coefficients of ${\lambda }^{-2N-1}$, ${\lambda }^{-2N}$, ${\lambda }^{2N+1}$, ${\lambda }^{2N+2}$ in (53), we have

$$\begin{array}{r}{P_{11}}^{(2)}=1,{P_{11}}^{(1)}(n)=0,{P_{11}}^{(0)}=0,\\ {P_{12}}^{(1)}=-M_n{a}_{n+1}^{(-2N-1)}+b_{n+1}^{(-2N)}=-{\tilde{M}}_n,\\ {P_{12}}^{(0)}=0,{P_{21}}^{(1)}=M_n{a}_{n+1}^{(-2N-1)}-b_{n+1}^{(-2N)}={\tilde{M}}_n,\\ {P_{21}}^{(0)}=0,{P_{22}}^{(0)}=1.\end{array}$$

(54)

From (23) and (54), we see that $P_n={\tilde{U}}_n$.

Next, we will prove that the matrix ${\tilde{V}}_n$ has the same form as $V_n$ under transformations (22) and (32).

Let

$$(T_{n,t}+T_n{V}_n)T_n^{\ast }=\left(\begin{array}{cc}{g}_{11}(\lambda ,n)& g_{12}(\lambda ,n)\\ g_{21}(\lambda ,n)& g_{22}(\lambda ,n)\end{array}\right).$$

(55)

It can be verified that the highest order of $g_{12}(\lambda ,n)$ and $g_{21}(\lambda ,n)$ is $4N+4$, the lowest order is $-4N-4$, and the highest and lowest orders of $g_{11}(\lambda ,n)$, $g_{22}(\lambda ,n)$ are $4N+3$ and $-4N-3$ respectively.

Using (20), (21), (25) and (27), we can obtain

$$\begin{array}{r}{a}_{n,t}({\lambda }_i)=-{\delta }_{i,n,t}{b}_n({\lambda }_i)-{\delta }_{i,n}{b}_{n,t}({\lambda }_i),c_{n,t}({\lambda }_i)=-{\delta }_{i,n,t}{d}_n({\lambda }_i)-{\delta }_{i,n}{d}_{n,t}({\lambda }_i),\\ {\delta }_{i,n,t}={\lambda }_i{M}_{n-1}+\frac{M_n}{{\lambda }_i}+(-{\lambda }_i^2+\frac{1}{{\lambda }_i^2}){\delta }_{i,n}+(\lambda M_n+\frac{M_{n-1}}{{\lambda }_i}){\delta }_{i,n}^2.\end{array}$$

(56)

From (56), we can prove that $g_{11}({\lambda }_i,n)$, $g_{12}({\lambda }_i,n)$, $g_{21}({\lambda }_i,n)$ and $g_{22}({\lambda }_i,n)$ are all zeroes (the detailed proof is omitted). Moreover, we have

$$(T_{n,t}+T_n{V}_n)T_n^{\ast }=det{T}_n\cdot R_n,$$

(57)

with

$$R_n=\left(\begin{array}{cc}{R}_{1,1}& R_{1,2}\\ R_{2,1}& R_{2,2}\end{array}\right),$$

(58)

where

$$\begin{array}{c}{R}_{1,1}={R_{11}}^{(2)}{\lambda }^2+{R_{11}}^{(1)}\lambda +{R_{11}}^{(-1)}/\lambda +{R_{11}}^{(-2)}/{\lambda }^2+{R_{11}}^{(0)},\hfill \\ R_{1,2}={R_{12}}^{(1)}\lambda +{R_{12}}^{(0)}+{R_{12}}^{(-1)}/\lambda ,\hfill \\ R_{2,1}={R_{21}}^{(1)}\lambda +{R_{21}}^{(0)}+{R_{21}}^{(-1)}/\lambda ,\hfill \\ R_{2,2}={R_{22}}^{(2)}{\lambda }^2+{R_{22}}^{(1)}\lambda +{R_{22}}^{(-2)}/{\lambda }^2+{R_{22}}^{(-1)}/\lambda +{R_{22}}^{(0)}.\hfill \end{array}$$

Thus, we obtain

$$T_{n,t}+T_n{V}_n=R_n{T}_n.$$

(59)

Using (27), (50) and (59), and comparing the coefficients of ${\lambda }^{2N+3}$, ${\lambda }^{2N+2}$, ${\lambda }^{2N+1}$, ${\lambda }^{-2N-1}$, ${\lambda }^{-2N-2}$, ${\lambda }^{-2N-3}$ in (59), we have

$$\begin{array}{r}{R_{11}}^{(2)}=1/2,{R_{11}}^{(1)}=0,{R_{11}}^{(-2)}=-1/2,{R_{11}}^{(-1)}=0,\\ {R_{12}}^{(0)}=0,{R_{21}}^{(0)}=0,{R_{12}}^{(-1)}=-M_{n-1}{a}_n^{(-2N-1)}+b_n^{(-2N)}=-{\tilde{M}}_{n-1},\\ {R_{22}}^{(-1)}=0,{R_{21}}^{(1)}=M_{n-1}{a}_n^{(-2N-1)}-b_n^{(-2N)}={\tilde{M}}_{n-1},{R_{22}}^{(-2)}=1/2,\\ {R_{22}}^{(2)}=-1/2,{R_{22}}^{(1)}=0\end{array}$$

(60)

and

$$\begin{array}{r}{R_{11}}^{(0)}={R_{12}}^{(1)}{b}_n^{(-2N)}+M_{n-1}{b}_n^{(2N)}+M_n{M}_{n-1},\\ {R_{12}}^{(1)}=-(b_n^{(-2N)}+M_n)/a_n^{(-2N-1)},\\ {R_{21}}^{(-1)}=(b_n^{(-2N)}+M_n)/a_n^{(-2N-1)},\\ {R_{22}}^{(0)}=-{R_{21}}^{(-1)}{b}_n^{(-2N)}+M_{n-1}{b}_n^{(2N)}+M_n{M}_{n-1}.\end{array}$$

(61)

In addition, from (53) we can obtain the following relation:

$$a_n^{(-2N-1)}{\tilde{M}}_n-b_n^{(-2N)}-M_n=0.$$

(62)

Substituting (62) into (61), from (32), we can derive

$${R_{11}}^{(0)}={\tilde{M}}_n{\tilde{M}}_{n-1},{R_{12}}^{(1)}=-{\tilde{M}}_n,{R_{21}}^{(-1)}={\tilde{M}}_n,{R_{22}}^{(0)}={\tilde{M}}_n{\tilde{M}}_{n-1}.$$

(63)

From (24), (60), (61) and (63), we can see that $R_n={\tilde{V}}_n$. The theorem is proved. □