Abstract
This paper is concerned with obtaining the approximate solution of a class of semi-explicit Integral Algebraic equations (IAEs) of index-1 with weakly singular kernels. Some function transformations and variable transformations are used to change the equations into integral equations defined on the standard interval , so that the solution of the new system possesses better regularity and the Jacobi orthogonal polynomial theory can be applied conveniently. A Jacobi collocation method is proposed and its convergence analysis is provided, which theoretically justifies the spectral rate of convergence. The numerical results are given to verify our theoretical analysis.
MSC:65R20.
Similar content being viewed by others
1 Introduction
In this paper, we consider the following system of Volterra Integral equations (VIEs) with weakly singular kernels:
where (, ), the functions , and () are known to be smooth on I and , respectively, and , are unknown solutions. We assume that , , . Under these conditions, system (1.1) is called a system of Weakly Singular Integral Algebraic equations (WSIAEs) of index 1. System (1.1) can be written in the following form:
where
In practical applications, one frequently encounters system (1.1). A good source on applications of IAEs with weakly singular kernels is the initial (boundary) value problems for the semi-infinite strip and temperature boundary specification including two/three-phase inverse Stefan problems [1–4]. A wide ranging description of IAEs arising in applications is given in [5]. Several numerical methods for integral algebraic equations have been proposed (see e.g. [5–10]). However, as far as we know the numerical analysis of WSIAEs is largely incomplete and this is a new topic for research. The existence and uniqueness for the solution of WSIAEs has been given in [11, 12]. The piecewise polynomial collocation method for system (1.1) and the concept of tractability index have been considered by Brunner [5]; he analyzed the regularity of the solutions using conditions that hold for the first and second kind Volterra integral equations. Recently, the effective numerical method based on the Chebyshev collocation scheme is designed for system (1.1) in [13] and its convergence analysis is provided.
The solutions of system (1.1) usually have a weak singularity at , whose derivatives are unbounded at . To overcome this difficulty, we use the idea of the authors in [14]. Both function transformation and variable transformation are used to change the system into a new system defined on the standard interval , so that the solutions of the new system possess better regularity and the Jacobi spectral collocation method can be applied conveniently. The aim of this work is to use the Jacobi collocation method to numerically solve the WSIAEs (1.1) and then a rigorous error analysis is provided in the weighted -norm which shows the spectral rate of convergence is attained.
This paper is organized as follows. Some useful results for establishing the convergence results will be provided in Section 2. In Section 3, we carry out the Jacobi collocation approach for system (1.1). The convergence of the method in the weighted -norm as a main result of the paper is given in Section 4. Section 5 gives some numerical experiments. The final section contains conclusions and remarks.
2 Some useful results
In this section, we discuss how the weakly singular IAEs can be changed to treat the problem. Furthermore, the index concept for WSIAEs which plays a fundamental role in both the analysis and the development of numerical algorithms for IAEs is discussed.
2.1 Index definitions for WSIAEs
There are several definitions of index in literature, not all completely equivalent, such as the tractability index (see, e.g. Definition (8.1.7) from [5]), the left index [6] and differentiation index [15]. Generally, the difficulties are arising in the theoretical and numerical analysis of IAEs relevant to the index notion.
In this paper, we use the concept of the differentiation index which measures how far the main WSIAE is apart from a regular system of VIEs. Namely, the number of analytical differentiations of system (1.1) until it can be formulated as a regular system of Volterra integral equations is called the differentiation index.
Now, we consider the index of system (1.1). According to the classical theory of Volterra integral equations with weakly singular kernels from [[5], p.353], if we multiply both sides of the second equation of (1.1) by the factor and integrate with respect to t, the following first kind Volterra integral equation with regular bounded kernels will be obtained:
where
and
We get the following second kind integral equation by differentiation of equation (2.1):
where () and . In fact, can be obtained using integration by parts to with .
Because , we have , then equation (2.2) together with the first equation of (1.1) is a system of regular Volterra integral equation.
But it should be noted that this reduction (differentiation) is not useful from a numerical point of view and such a definition may be useful for understanding the underlying mathematical structure of a WSIAEs, and hence choosing a suitable numerical method for their solutions.
2.2 Smoothness of the solution
We assume that the Hölder space is defined to be a subspace of that consists of functions which are Hölder continuous with the exponent β. For and , we similarly define the Hölder space
It is shown in [16] that this is a Banach space with the following norm:
It is noted that the solutions of system (1.1) and lie in the Hölder space and , respectively (see [[5], Theorems 8.1.8, 6.1.6, and 6.1.14]). In other words, for any positive integer m, the solutions and do not belong to . It is well known that the spectral methods have been an efficient tool for solving the differential equations with smooth solutions. Using the idea of Li and Tang in [14], one can overcome this difficulty by introducing the following variable transformation:
to change (1.1) to the following system:
where
and , are the smooth solutions of system (2.4).
The existence and uniqueness results and the smoothness behavior of solutions and of system (2.4) can be obtained from the corresponding discussions of the classical theory of Volterra integral equations with weakly singular kernels from [5] (see e.g. Theorems 6.1.6 and 6.1.14 for further details).
3 The Jacobi collocation method
We first introduce some notations. Let () be a weight function in the usual sense. As defined in [17], let us denote the Jacobi polynomial of degree n with respect to weight . It is well known that the set of Jacobi polynomials forms a complete orthogonal system, where is the space of functions with , and
Particularly, when , the Jacobi polynomials become Legendre polynomials, and when , the Jacobi polynomials become Chebyshev polynomials.
For the sake of obtaining a Jacobi spectral method for system (2.4), we employ the linear transformation
to rewrite system (2.4) as follows:
where , , , , and
It is well known that, in the Jacobi collocation method, we use and of the following form:
to approximate the solutions and , where are the Gauss-Jacobi quadrature points and are the interpolating Lagrange polynomials
where is the th-order Jacobi polynomial.
Now, we fix the value of v for general kernels and choose , then can be approximated by a univariate Lagrange interpolating polynomial as follows:
Substituting equations (3.3) and (3.5) into (3.2) and inserting the collocation points () in the obtained equation, one obtains the following system of linear equations:
So, the unknown coefficients and are obtained by solving the linear system (3.6) and finally the approximate solutions and will be computed by substituting these coefficients into (3.3).
4 Error estimate
To prove the error estimate in the weighted -norm, we first introduce some lemmas which are usually required to obtain the convergence results.
Lemma 1 ([18])
Let be a linear operator from to , then , , there exists a positive constant , such that , , s.t., .
Lemma 2 ([14])
Let be Lagrange interpolation polynomials with the Jacobi Gauss points , then
Let , denote the error functions. The following main theorem reveals the convergence results of the presented scheme in the weighted -norm.
Theorem 1 Consider the index-1 weakly singular integral algebraic equations (1.1) and its transformed representation (3.2). Let , be the approximated solution for the exact solution of (3.2) based on the spectral collocation scheme (3.6) and suppose the following conditions hold:
-
(1)
(), ;
-
(2)
(), with ;
-
(3)
, .
Then for sufficiently large N,
where .
Proof First, the first equation of system (3.6) can be rewritten as
where
and
Using these notations, equation (4.1) can be written as
where
Multiplying equation (4.2) by and summing up from 0 to N, one obtains
and subtracting equation (4.4) from the first equation of (3.2), we have
where
Equation (4.5) can be rewritten as follows:
where
Next, by using the second equation of (3.2), we have
For the second equation of (3.6), using a similar procedure as outlined for obtaining the relation (4.4), and then inserting equation (4.7) into the resulting equation, we get
where
and
Using a similar method for obtaining equation (2.1) in Section 2, equation (4.8) can be written as
where , .
On differentiation of equation (4.9) with respect to v, we obtain a second kind integral equation as follows:
where
Now, we rewrite equation (4.10) as
equations (4.6) and (4.12) can be written in the form of the compact matrix representation:
where
From equation (2.2), and , and from the condition (3) of Theorem 1, , , so the matrix is invertible and its inverse can be written as
Multiplying equation (4.13) by yields
where and .
By the generalized Gronwall inequality [[19], Lemma (3.6)], one obtains
It follows from the generalized Hardy inequality [[14], Lemma 5] that
From now on, for simplicity, we denote by and try to derive the error bounds for the proposed method step by step.
Step 1: We now estimate the error bounds for (). Since denotes the interpolation operator, we have
It is noted that
where is defined in Lemma 1, and
Using Lemma 1 for , Lemma 2, and Lemma (3.5) from [19], we obtain
Then using the inequality (5.5.28) from [17], we have
Here
Similarly,
Step 2: In this step, we estimate and . Using Lemma 2, we have
Furthermore, from (4.3) we obtain
Using the transformation (3.1), we have
where denotes the Euler Beta function. Then using the inequality (5.5.28) from [17], we have
From (4.21), we obtain
where
Similarly, we have
Step 3: Here, our aim is to find a bound for using the suitable inequalities as well as the previously obtained bounds. Therefore, we estimate equation (4.11) as
By using the generalized Hardy inequality from [14], it can be seen that
Using the inequality (5.5.25) from [17], we have
where .
Let in (4.19), we have
Moreover, using integration by parts and the generalized Hardy inequality, we have
Now, using the inequalities (5.5.22) and (5.5.25) from [17] yields
Similarly,
On the other hand, using the inequality (5.5.4) from [17] and equation (4.22), we obtain
Also we have
Finally, the above estimates together with equation (4.16) lead to Theorem 1. □
It is noted in [20] that the function transformation generally makes the resulting equations and approximations more complicated. As discussed in [[14], p.80], we can also obtain the error estimates for the numerical solutions to the WSIAEs (1.1).
Theorem 2 Consider the index-1 WSIAEs (1.1). Let be the spectral collocation approximation for the exact solution of system (1.1), and suppose the following conditions hold:
-
(1)
(), ;
-
(2)
(), with ;
-
(3)
, .
Then for sufficiently large N,
where .
5 Numerical experiments
In [14, 19, 21], the authors have analyzed the spectral Jacobi collocation method for Volterra integral equations of the second kind with singular kernel. Here, we consider the approximate solution for coupled system of weakly singular integral algebraic equations which consist of both the first and the second kind Volterra integral equations. To our knowledge, there are no other results as regards the numerical analysis of WSIAEs except [13], which designed an effective numerical method based on the Chebyshev collocation scheme for system (1.1) and provided its convergence analysis. It is noted that the Jacobi collocation method becomes the Chebyshev collocation method for . In this section, some numerical examples are given to show the validity of the proposed method. Variable transformations (2.3) and linear transformations (3.1) are used to change the WSIAEs system into a new system such that its solutions have better regularity. All the computations were performed using the software Matlab®. These problems are solved using the Jacobi collocation method for , . In order to show the behavior of the errors, we define the weighted -norm by
where () is the Jacobi weight function.
Example 1 Consider the following index-1 WSIAEs system:
where
and , are chosen such that the exact solution is
Because , , it is noted that and at . For , by using variable transformation , the smooth solutions , are obtained. Inserting , in the WSIAEs and using the transformation (3.1), we have
where
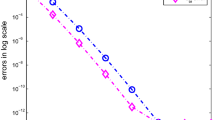
Let denote the approximation of the exact solution that is given by equation (3.3). The proposed Jacobi collocation methods are applied for system (5.1). Table 1 shows the errors for . It is seen that the desired exponential rate of convergence is obtained.
Example 2
where
and , are chosen such that the exact solution is
In Table 2 we present the weighted -norm of errors for the numerical solutions by using the spectral collocation method.
6 Conclusions
This work has been concerned with the theoretical and numerical analysis of integral algebraic equations of index 1 with weakly singular kernels. It is noted that the solutions of the WSIAEs are not sufficiently smooth. So, the original system was changed into a new system, by using some function transformations and variable transformations. We presented a spectral Jacobi collocation approximation for the new WSIAEs. The error estimation of the method in the weighted -norm was obtained. Numerical results are presented to confirm the theoretical prediction of the exponential rate of convergence.
References
Cannon JR: The One-Dimensional Heat Equation. Cambridge University Press, Cambridge; 1984.
Gomilko AM: A Dirichlet problem for the biharmonic equation in a semi-infinite strip. J. Eng. Math. 2003, 46: 253–268. 10.1023/A:1025065714786
Goldman NL Mathematics and Its Applications 412. In Inverse Stefan Problems. Kluwer Academic, Dordrecht; 1997.
Slodička M, Schepper HD: Determination of the heat-transfer coefficient during solidification of alloys. Comput. Methods Appl. Mech. Eng. 2005, 194: 491–498. 10.1016/j.cma.2004.04.010
Brunner H: Collocation Methods for Volterra Integral and Related Functional Equations. Cambridge University Press, Cambridge; 2004.
Bulatov MV, Chistyakov VF: The Properties of Differential-Algebraic Systems and Their Integral Analogs. Memorial University of Newfoundland, Newfoundland; 1997.
Bulatov MV: Regularization of singular system of Volterra integral equation. Comput. Math. Math. Phys. 2002, 42: 315–320.
Bulatov MV, Lima PM: Two-dimensional integral-algebraic systems: analysis and computational methods. J. Comput. Appl. Math. 2011, 236: 132–140. 10.1016/j.cam.2011.06.001
Hadizadeh M, Ghoreishi F, Pishbin S: Jacobi spectral solution for integral-algebraic equations of index-2. Appl. Numer. Math. 2011, 61: 131–148. 10.1016/j.apnum.2010.08.009
Pishbin S, Ghoreishi F, Hadizadeh M: A posteriori error estimation for the Legendre collocation method applied to integral-algebraic Volterra equations. Electron. Trans. Numer. Anal. 2011, 38: 327–346.
Brunner H, Bulatov MV: On singular systems of integral equations with weakly singular kernels. Proceeding 11-th Baikal International School Seminar 1998, 64–67.
Bulatov, MV, Lima, PM, Weinmuller, E: Existence and uniqueness of solutions to weakly singular integral-algebraic and integro-differential equations. Vienna Technical University, ASC Report No. 21 (2012)
Pishbin S, Ghoreishi F, Hadizadeh M: The semi-explicit Volterra integral algebraic equations with weakly singular kernels: the numerical treatments. J. Comput. Appl. Math. 2013, 245: 121–132.
Li X, Tang T: Convergence analysis of Jacobi spectral collocation methods for Abel-Volterra integral equations of second kind. Front. Math. China 2012, 7: 69–84. 10.1007/s11464-012-0170-0
Gear CW: Differential algebraic equations, indices, and integral algebraic equations. SIAM J. Numer. Anal. 1990, 27: 1527–1534. 10.1137/0727089
Atkinson K, Han W: Theoretical Numerical Analysis: A Functional Analysis Framework. Springer, New York; 2009.
Canuto C, Hussaini MY, Quarteroni A, Zang TA: Spectral Methods Fundamentals in Single Domains. Springer, Berlin; 2006.
Graham IG, Sloan IH:Fully discrete spectral boundary integral methods for Helmholtz problems on smooth closed surfaces in . Numer. Math. 2002, 92: 289–323. 10.1007/s002110100343
Chen Y, Tang T: Convergence analysis of the Jacobi spectral collocation methods for Volterra integral equations with a weakly singular kernel. Math. Comput. 2010, 79: 147–167. 10.1090/S0025-5718-09-02269-8
Diogo T, McKee S, Tang T: Collocation methods for second-kind Volterra integral equations with weakly singular kernels. Proc. R. Soc. Edinb. A 1994, 124: 199–210. 10.1017/S0308210500028432
Chen Y, Tang T: Spectral methods for weakly singular Volterra integral equations with smooth solutions. J. Comput. Appl. Math. 2009, 233: 938–950. 10.1016/j.cam.2009.08.057
Acknowledgements
The authors would like to acknowledge the anonymous referees for their careful reading of the manuscript and constructive comments. This work is supported by the National Natural Science Foundation of China (11101109, 11271102), Natural Science Foundation of Hei-long-jiang Province of China (A201107) and SRF for ROCS, SEM.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
A retraction note to this article can be found online at http://dx.doi.org/10.1186/s13662-015-0516-5.
An erratum to this article is available at http://dx.doi.org/10.1186/s13662-015-0516-5.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhao, J., Wang, S. Jacobi spectral solution for weakly singular integral algebraic equations of index-1. Adv Differ Equ 2014, 165 (2014). https://doi.org/10.1186/1687-1847-2014-165
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-165