Convergence analysis of algorithms for memristive oscillator system

Abstract

Memristive oscillator systems are common models for many problems in physics, engineering, and systems biology. This paper presents a convergence analysis of two types of algorithms for solving a fourth-order memristive oscillator system. For the first algorithm, a parallel algorithm, a limiting state of the iterate sequence generated by a Jacobi iterative scheme and the Euler polygonal method, is a solution of the system under some weaker conditions. With the second algorithm, a partial difference method, which is based on the partial difference concept and exponential convergence, is also presented. The proposed algorithms in this paper can be applied to general nonlinear hybrid systems.

1 Introduction

Recently, a large number of applications for memristive oscillator systems have been reported, including nonvolatile memristor memories, digital and analog circuits; see [1–10]. The models of memristive oscillator systems suggest possible responses of simple intelligences in biomimetics as well as new approaches for bio-inspired reconfigurable circuits. Considerable attention has been devoted to the theoretical properties of memristive oscillator systems, and their relationship to memristor dynamics (see [1–4, 6, 9, 10] and references therein). A very lower dimensional memristor equation can appear with complex double-loop behavior. Therefore, the memristive system is a complicated system that has strongly nonlinear behavior, as it includes the switched network cluster and shows a high uncertainty [11]. Deep studies of the memristive system are important in various applications due to the important guiding role in memristor-based physical commercially available devices. For example, nonlinear dynamics has been shown to play an important role in the understanding of a wide spectrum of memristor-based technological and biological systems [1–4, 6, 9–11].

In this paper, we consider a fourth-order memristive oscillator system described by the following differential equations:

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_{1}R}{v}_2(t)-\frac{1}{C_{1}R}{v}_1(t)-\frac{1}{C_1}W(\phi (t))v_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_{2}R}{v}_1(t)-\frac{1}{C_{2}R}{v}_2(t)-\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=\frac{1}{L}{v}_2(t),\end{array}$$

(1)

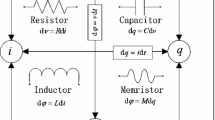
where $v_1(t)$ and $v_2(t)$ denote voltages, $C_1$ and $C_2$ represent capacitors, $W(\phi (t))$ is a memductance function, and $\phi (t)$, $\ell (t)$, R, and L are magnetic flux, current, resistor, and inductor, respectively.

Using the mathematical model of a piecewise-linear memristor [3, 4], the memductance function $W(\phi )$ is characterized by

$$W(\phi )=\{\begin{array}{ll}{a}_1,& |\phi |<1,\\ a_2,& |\phi |>1,\end{array}$$

(2)

where $a_1$ and $a_2$ are parameters.

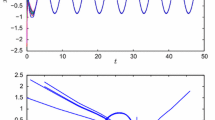
Choose parameters $C_1=5.5\text{nF}$, $C_2=49.5\text{nF}$, $L=7.07\text{mH}$, $R=1\text{,}428\mathrm{\Omega }$, $a_1=-0.8\times {10}^{-3}$, $a_2=-0.5\times {10}^{-3}$, and set the initial condition $\phi (0)=0.1$, $v_1(0)=0.1$, $v_2(0)=0.1$, $\ell (0)=0.1$; we can see that system (1) indeed generates chaotic behavior. Simulated results are depicted in Figures 1 and 2. Figure 1 displays the projections of the chaotic attractor of system (1) in the three-dimensional space. To get a better view of this chaotic attractor, Figure 2 shows the projections of the chaotic attractor of system (1) in the two-dimensional space.

Figure 1

Phase portraits of the chaotic system ( 1 ) in the three-dimensional space.

Figure 2

Phase portraits of the chaotic system ( 1 ) in the two-dimensional space.

To solve the state-dependent nonlinearity of system (1), fuzzy logic has attracted much attention as a powerful tool. The memristive oscillator system (1) can be represented as the following fuzzy model:

Rule 1: If $|\phi |<1$, then

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_{1}R}{v}_2(t)-\frac{1}{C_{1}R}{v}_1(t)-\frac{1}{C_1}{a}_1{v}_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_{2}R}{v}_1(t)-\frac{1}{C_{2}R}{v}_2(t)-\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=\frac{1}{L}{v}_2(t).\end{array}$$

(3)

Rule 2: If $|\phi |>1$, then

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_{1}R}{v}_2(t)-\frac{1}{C_{1}R}{v}_1(t)-\frac{1}{C_1}{a}_2{v}_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_{2}R}{v}_1(t)-\frac{1}{C_{2}R}{v}_2(t)-\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=\frac{1}{L}{v}_2(t).\end{array}$$

(4)

With a center-average defuzzier, the over-fuzzy system in (3) and (4) is represented as

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)=\frac{1}{C_{1}R}{v}_2(t)-\frac{1}{C_{1}R}{v}_1(t)-\frac{1}{C_1}({\sum }_{i=1}^2{\eta }_i(t)a_i)v_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_{2}R}{v}_1(t)-\frac{1}{C_{2}R}{v}_2(t)-\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=\frac{1}{L}{v}_2(t),\end{array}$$

(5)

where

$${\eta }_1(t)=\{\begin{array}{ll}1,& |\phi |<1,\\ 0,& |\phi |>1,\end{array}{\eta }_2(t)=\{\begin{array}{ll}0,& |\phi |<1,\\ 1,& |\phi |>1.\end{array}$$

Notwithstanding the vast literature on nonlinear dynamical systems, the majority of the existing studies focus on memristive oscillator systems whose inner mechanisms have never been thoroughly studied and expounded. This can mainly be attributed to the memristor nonlinearity. One such challenge in the memristive system is a state-dependent nonlinear network cluster [11]. As a result, the monitoring, control, and optimization in memristive systems will be extremely difficult.

An important research problem is to develop some rigorous algorithm theories and design tactics for solving memristive oscillator systems. Algorithm theories represent the structure common to a class of algorithms, which can provide the basis for designing tactics-specialized methods for analyzing memristive oscillator systems. The memristive differential system which is described by a state-dependent nonlinear network cluster presents a difficulty in numerical integration, since the conventional processing approaches make it hard to achieve satisfactory results. In general, solving these problems requires overcoming a number of theoretically challenging issues and even developing entirely new analytical methods. A key open problem is how to devise effective algorithms for dealing with the characteristics of memristive system. Generally, to the best of our knowledge, no relevant work as regards the algorithms and their convergence for memristive oscillator systems has been reported.

The objective of this paper is to develop some algorithms and analyze their corresponding convergence properties. This consideration does not only have theoretical value but also practical meaning. For the numerical solution of complex systems and networks, of the many methods available, a parallel algorithm and a partial difference method show good feasibility and advantages. Thus, these two algorithms are chosen for memristive oscillator systems. The constructive proofs in this paper are able to fully demonstrate that the parallel algorithm and the partial difference method have a general applicability that can make them popular in a wide variety of cases. We believe the basic algorithm and convergence in theory for memristive systems should be a significant research topic due to the potential in a variety of emerging applications.

2 Parallel algorithm

In this section, we give a constructive proof on the parallel algorithm and its convergence for system (1).

By the theories of differential inclusions and set-valued maps, from (5), it follows that

$$\{\begin{array}{l}\dot{\phi }(t)=v_1(t),\\ {\dot{v}}_1(t)\in \frac{1}{C_{1}R}{v}_2(t)-\frac{1}{C_{1}R}{v}_1(t)-\frac{1}{C_1}(co\{a_1,a_2\})v_1(t),\\ {\dot{v}}_2(t)=\frac{1}{C_{2}R}{v}_1(t)-\frac{1}{C_{2}R}{v}_2(t)-\frac{1}{C_2}\ell (t),\\ \dot{\ell }(t)=\frac{1}{L}{v}_2(t),\end{array}$$

(6)

where $co\{a_1,a_2\}$ denotes a closure of the convex hull generated by real numbers $a_1$ and $a_2$.

Transform (6) into the compact form as follows:

$$\dot{\mathrm{\Theta }}\in \left(\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{1}{C_{1}R}-\frac{1}{C_1}co\{a_1,a_2\}& \frac{1}{C_{1}R}& 0\\ 0& \frac{1}{C_{2}R}& -\frac{1}{C_{2}R}& -\frac{1}{C_2}\\ 0& 0& \frac{1}{L}& 0\end{array}\right)\mathrm{\Theta }:=A\mathrm{\Theta },$$

(7)

where the vector $\mathrm{\Theta }={(\phi (t),v_1(t),v_2(t),\ell (t))}^T$,

$$matrixA=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{1}{C_{1}R}-\frac{1}{C_1}co\{a_1,a_2\}& \frac{1}{C_{1}R}& 0\\ 0& \frac{1}{C_{2}R}& -\frac{1}{C_{2}R}& -\frac{1}{C_2}\\ 0& 0& \frac{1}{L}& 0\end{array}\right).$$

In (7), split the matrix A into matrices B and C, i.e., $A=B+C$, where

$$\begin{array}{c}B=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& -\frac{1}{C_{1}R}-\frac{1}{C_1}co\{a_1,a_2\}& 0& 0\\ 0& 0& -\frac{1}{C_{2}R}& 0\\ 0& 0& 0& 0\end{array}\right),\hfill \\ C=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& \frac{1}{C_{1}R}& 0\\ 0& \frac{1}{C_{2}R}& 0& -\frac{1}{C_2}\\ 0& 0& \frac{1}{L}& 0\end{array}\right).\hfill \end{array}$$

Obviously, according to the Jacobi iterative scheme,

$$\{\begin{array}{l}\dot{y}=By+C{\mathrm{\Theta }}^k,y(0)=\mathrm{\Theta }(0),\\ {\mathrm{\Theta }}^{k+1}={\mathrm{\Theta }}^k+\omega (y-{\mathrm{\Theta }}^k),\end{array}$$

(8)

where $y=y(t)={(y_1(t),y_2(t),y_3(t),y_4(t))}^T$, ${\mathrm{\Theta }}^k={\mathrm{\Theta }}^k(t)={({\phi }^k(t),v_1^k(t),v_2^k(t),{\ell }^k(t))}^T$, $\omega \ne 0$ is a constant.

Let $t_0=0$, $t_n=t_0+nh$, denote $y_n=y(t_n)={(y_1(t_n),y_2(t_n),y_3(t_n),y_4(t_n))}^T$, ${\mathrm{\Theta }}_n^k={\mathrm{\Theta }}^k(t_n)={({\phi }^k(t_n),v_1^k(t_n),v_2^k(t_n),{\ell }^k(t_n))}^T$, and applying the Euler polygonal method, by (8), it follows that

$$\{\begin{array}{l}\frac{y_n-y_{n-1}}{h}=B{y}_n+C{\mathrm{\Theta }}_n^k,\\ {\mathrm{\Theta }}_n^{k+1}={\mathrm{\Theta }}_n^k+\omega (y_n-{\mathrm{\Theta }}_n^k),\end{array}$$

(9)

then

$$\{\begin{array}{l}(I-hB)y_n=y_{n-1}+hC{\mathrm{\Theta }}_n^k,\\ {\mathrm{\Theta }}_n^{k+1}=(1-\omega ){\mathrm{\Theta }}_n^k+\omega y_n,\end{array}$$

(10)

where I is the $4\times 4$ identity matrix.

Through the first equation of (10),

$$y_n={(I-hB)}^{-1}{y}_{n-1}+h{(I-hB)}^{-1}C{\mathrm{\Theta }}_n^k=D{y}_{n-1}+hDC{\mathrm{\Theta }}_n^k,$$

(11)

where matrix $D={(I-hB)}^{-1}$. Besides, for (11), if the matrix $I-hB$ is invertible, then $D={(I-hB)}^{-1}$ is the general inverse matrix, otherwise $D={(I-hB)}^{-1}$ is the generalized inverse matrix.

Substitute (11) into the second equation of (10),

$$\begin{array}{rcl}{\mathrm{\Theta }}_n^{k+1}& =& (1-\omega ){\mathrm{\Theta }}_n^k+\omega (D{y}_{n-1}+hDC{\mathrm{\Theta }}_n^k)\\ =& [(1-\omega )I+\omega hDC]{\mathrm{\Theta }}_n^k+\omega D{y}_{n-1}=F{\mathrm{\Theta }}_n^k+\omega D{y}_{n-1},\end{array}$$

(12)

where the matrix $F=(1-\omega )I+\omega hDC$. Therefore, we get

$${\mathrm{\Theta }}_1^{k+1}=F{\mathrm{\Theta }}_1^k+\omega D{y}_0,\text{when }n=1,$$

(13)

$${\mathrm{\Theta }}_2^{k+1}=F{\mathrm{\Theta }}_2^k+\omega D{y}_1,\text{when }n=2.$$

(14)

On the other hand, by (11),

$$y_1=D{y}_0+hDC{\mathrm{\Theta }}_1^k,$$

(15)

thus

$${\mathrm{\Theta }}_2^{k+1}=F{\mathrm{\Theta }}_2^k+\omega D(D{y}_0+hDC{\mathrm{\Theta }}_1^k)=F{\mathrm{\Theta }}_2^k+\omega h{D}^{2}C{\mathrm{\Theta }}_1^k+\omega D^2{y}_0,$$

(16)

through using the method of induction, and then

$${\mathrm{\Theta }}_n^{k+1}=F{\mathrm{\Theta }}_n^k+\omega h{D}^{2}C{\mathrm{\Theta }}_{n-1}^k+\cdots +\omega h{D}^{n}C{\mathrm{\Theta }}_1^k+\omega D^n{y}_0.$$

(17)

In fact, it is not difficult to find that

$$\begin{array}{rcl}F& =& (1-\omega )I+\omega hDC\\ =& (1-\omega )I+\omega h{(I-hB)}^{-1}C\\ =& (1-\omega )I+\omega h{\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1+\frac{h}{C_{1}R}+\frac{h}{C_1}co\{a_1,a_2\}& 0& 0\\ 0& 0& 1+\frac{h}{C_{2}R}& 0\\ 0& 0& 0& 1\end{array}\right)}^{-1}\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& \frac{1}{C_{1}R}& 0\\ 0& \frac{1}{C_{2}R}& 0& -\frac{1}{C_2}\\ 0& 0& \frac{1}{L}& 0\end{array}\right)\\ =& (1-\omega )I+\omega h\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \frac{1}{1+\frac{h}{C_{1}R}+\frac{h}{C_1}co\{a_1,a_2\}}& 0& 0\\ 0& 0& \frac{1}{1+\frac{h}{C_{2}R}}& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& \frac{1}{C_{1}R}& 0\\ 0& \frac{1}{C_{2}R}& 0& -\frac{1}{C_2}\\ 0& 0& \frac{1}{L}& 0\end{array}\right)\\ =& (1-\omega )I+\omega h\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& \frac{1}{1+\frac{h}{C_{1}R}+\frac{h}{C_1}co\{a_1,a_2\}}\frac{1}{C_{1}R}& 0\\ 0& \frac{1}{1+\frac{h}{C_{2}R}}\frac{1}{C_{2}R}& 0& -\frac{1}{1+\frac{h}{C_{2}R}}\frac{1}{C_2}\\ 0& 0& \frac{1}{L}& 0\end{array}\right)\\ =& (1-\omega )I+\left(\begin{array}{cccc}0& \omega h& 0& 0\\ 0& 0& \frac{1}{1+\frac{h}{C_{1}R}+\frac{h}{C_1}co\{a_1,a_2\}}\frac{\omega h}{C_{1}R}& 0\\ 0& \frac{1}{1+\frac{h}{C_{2}R}}\frac{\omega h}{C_{2}R}& 0& -\frac{1}{1+\frac{h}{C_{2}R}}\frac{\omega h}{C_2}\\ 0& 0& \frac{\omega h}{L}& 0\end{array}\right)\\ =& \left(\begin{array}{cccc}1-\omega & \omega h& 0& 0\\ 0& 1-\omega & \frac{1}{1+\frac{h}{C_{1}R}+\frac{h}{C_1}co\{a_1,a_2\}}\frac{\omega h}{C_{1}R}& 0\\ 0& \frac{1}{1+\frac{h}{C_{2}R}}\frac{\omega h}{C_{2}R}& 1-\omega & -\frac{1}{1+\frac{h}{C_{2}R}}\frac{\omega h}{C_2}\\ 0& 0& \frac{\omega h}{L}& 1-\omega \end{array}\right).\end{array}$$

(18)

Clearly, by the iterative scheme (17), we can draw the conclusion of Theorem 1.

Theorem 1 If $\rho (F)<1$, then the iterative scheme (17) is convergent, i.e., (17) converges to a fixed state, where $\rho (F)$ denotes spectral radius of the matrix F.

Theorem 2 If $\parallel F\parallel <1$, then the iterative scheme (17) is convergent, i.e., (17) converges to a fixed state, where $\parallel F\parallel$ denotes the norm of the matrix F.

Proof Since $\rho (F)\le \parallel F\parallel <1$, according to Theorem 1, it follows that Theorem 2 holds. □

Theorem 3 The fixed state of iterative scheme (17) is the solution of system (1).

Proof When ${lim}_{k\to +\mathrm{\infty }}{\mathrm{\Theta }}^k={\mathrm{\Theta }}^{\ast }$, take the limit of (8), then

$$\{\begin{array}{l}\dot{y}=By+C{\mathrm{\Theta }}^{\ast },\\ {\mathrm{\Theta }}^{\ast }={\mathrm{\Theta }}^{\ast }+\omega (y-{\mathrm{\Theta }}^{\ast }),\end{array}$$

thus $y={\mathrm{\Theta }}^{\ast }$, which satisfies (1). □

3 Partial difference method

In this section, we present a constructive proof to illustrate the partial difference method and the related convergence analysis for system (1).

Through the theories of the Taylor formula and the partial difference method, from (5), it follows that

$$\begin{array}{c}\phi (t_k+h)=\phi (t_k)+h\dot{\phi }(t_k)+\frac{h^2}{2}\ddot{\phi }(t_k)=\phi (t_k)+h{v}_1(t_k)+{\frac{h^2}{2}\frac{\mathrm{d}{v}_1(t)}{\mathrm{d}t}|}_{t=t_k}\hfill \\ \phantom{\phi (t_k+h)}=\phi (t_k)+h{v}_1(t_k)+\frac{h}{2}\left[{h\frac{\mathrm{d}{v}_1(t)}{\mathrm{d}t}|}_{t=t_k}\right]\hfill \\ \phantom{\phi (t_k+h)}=\phi (t_k)+h{v}_1(t_k)+\frac{h}{2}[v_1(t_k+h)-v_1(t_k)],\hfill \end{array}$$

(19)

$$\begin{array}{c}{v}_1(t_k+h)=v_1(t_k)+h{\dot{v}}_1(t_k)+\frac{h^2}{2}{\ddot{v}}_1(t_k)\hfill \\ \phantom{v_1(t_k+h)}=v_1(t_k)+h[\frac{1}{C_{1}R}{v}_2(t_k)-\frac{1}{C_{1}R}{v}_1(t_k)-\frac{1}{C_1}(\sum _{i=1}^2{\eta }_i(t_k)a_i)v_1(t_k)]\hfill \\ \phantom{v_1(t_k+h)=}+\frac{h^2}{2}[{\frac{1}{C_{1}R}\frac{\mathrm{d}{v}_2(t)}{\mathrm{d}t}|}_{t=t_k}-{\frac{1}{C_{1}R}\frac{\mathrm{d}{v}_1(t)}{\mathrm{d}t}|}_{t=t_k}-{\frac{1}{C_1}(\sum _{i=1}^2{\eta }_i(t_k)a_i)\frac{\mathrm{d}{v}_1(t)}{\mathrm{d}t}|}_{t=t_k}]\hfill \\ \phantom{v_1(t_k+h)}=v_1(t_k)+h[\frac{1}{C_{1}R}{v}_2(t_k)-\frac{1}{C_{1}R}{v}_1(t_k)-\frac{1}{C_1}(\sum _{i=1}^2{\eta }_i(t_k)a_i)v_1(t_k)]\hfill \\ \phantom{v_1(t_k+h)=}+\frac{h}{2}[\frac{1}{C_{1}R}(v_2(t_k+h)-v_2(t_k))-\frac{1}{C_{1}R}(v_1(t_k+h)-v_1(t_k))\hfill \\ \phantom{v_1(t_k+h)=}-\frac{1}{C_1}(\sum _{i=1}^2{\eta }_i(t_k)a_i)(v_1(t_k+h)-v_1(t_k))],\hfill \end{array}$$

(20)

$$\begin{array}{c}{v}_2(t_k+h)=v_2(t_k)+h{\dot{v}}_2(t_k)+\frac{h^2}{2}{\ddot{v}}_2(t_k)\hfill \\ \phantom{v_2(t_k+h)}=v_2(t_k)+h[\frac{1}{C_{2}R}{v}_1(t_k)-\frac{1}{C_{2}R}{v}_2(t_k)-\frac{1}{C_2}\ell (t_k)]\hfill \\ \phantom{v_2(t_k+h)=}+\frac{h^2}{2}[{\frac{1}{C_{2}R}\frac{\mathrm{d}{v}_1(t)}{\mathrm{d}t}|}_{t=t_k}-{\frac{1}{C_{2}R}\frac{\mathrm{d}{v}_2(t)}{\mathrm{d}t}|}_{t=t_k}-{\frac{1}{C_2}\frac{\mathrm{d}\ell (t)}{\mathrm{d}t}|}_{t=t_k}]\hfill \\ \phantom{v_2(t_k+h)}=v_2(t_k)+h[\frac{1}{C_{2}R}{v}_1(t_k)-\frac{1}{C_{2}R}{v}_2(t_k)-\frac{1}{C_2}\ell (t_k)]\hfill \\ \phantom{v_2(t_k+h)=}+\frac{h}{2}[\frac{1}{C_{2}R}(v_1(t_k+h)-v_1(t_k))-\frac{1}{C_{2}R}(v_2(t_k+h)-v_2(t_k))\hfill \\ \phantom{v_2(t_k+h)=}-\frac{1}{C_2}(\ell (t_k+h)-\ell (t_k))],\hfill \end{array}$$

(21)

$$\begin{array}{c}\ell (t_k+h)=\ell (t_k)+h\dot{\ell }(t_k)+\frac{h^2}{2}\ddot{\ell }(t_k)=\ell (t_k)+h\frac{1}{L}{v}_2(t_k)+\frac{h^2}{2}\left[{\frac{1}{L}\frac{\mathrm{d}{v}_2(t)}{\mathrm{d}t}|}_{t=t_k}\right]\hfill \\ \phantom{\ell (t_k+h)}=\ell (t_k)+\frac{h}{L}{v}_2(t_k)+\frac{h}{2L}\left[{h\frac{\mathrm{d}{v}_2(t)}{\mathrm{d}t}|}_{t=t_k}\right]\hfill \\ \phantom{\ell (t_k+h)}=\ell (t_k)+\frac{h}{L}{v}_2(t_k)+\frac{h}{2L}[v_2(t_k+h)-v_2(t_k)],\hfill \end{array}$$

(22)

where $h\ne 0$ is a constant.

Equations (19)-(22) are a generic form of a first-order partial difference method for system (5). When $h>0$, (19)-(22) are said to be the forward partial difference method for system (5). When $h<0$, (19)-(22) are said to be the backward partial difference method for system (5).

In the following, we consider the convergence of the first-order partial difference method for system (5).

By (19)-(22), we obtain

$$\phi (t_k+h)-\frac{h}{2}{v}_1(t_k+h)=\phi (t_k)+\frac{h}{2}{v}_1(t_k),$$

(23)

$$\begin{array}{c}[1+\frac{h}{2C_{1}R}+\frac{h}{2C_1}(\sum _{i=1}^2{\eta }_i(t_k)a_i)]v_1(t_k+h)-\frac{h}{2C_{1}R}{v}_2(t_k+h)\hfill \\ =\frac{h}{2C_{1}R}{v}_2(t_k)+[1-\frac{h}{2C_{1}R}-\frac{h}{2C_1}(\sum _{i=1}^2{\eta }_i(t_k)a_i)]v_1(t_k),\hfill \end{array}$$

(24)

$$\begin{array}{c}-\frac{h}{2C_{2}R}{v}_1(t_k+h)+(1+\frac{h}{2C_{2}R})v_2(t_k+h)+\frac{h}{2C_2}\ell (t_k+h)\hfill \\ =\frac{h}{2C_{2}R}{v}_1(t_k)+(1-\frac{h}{2C_{2}R})v_2(t_k)-\frac{h}{2C_2}\ell (t_k),\hfill \end{array}$$

(25)

$$\ell (t_k+h)-\frac{h}{2L}{v}_2(t_k+h)=\ell (t_k)+\frac{h}{2L}{v}_2(t_k).$$

(26)

Transform (23)-(26) into the compact form as follows:

$$\begin{array}{c}\left(\begin{array}{cccc}1& -\frac{h}{2}& 0& 0\\ 0& 1+\frac{h}{2C_{1}R}+\frac{h}{2C_1}({\sum }_{i=1}^2{\eta }_i(t_k)a_i)& -\frac{h}{2C_{1}R}& 0\\ 0& -\frac{h}{2C_{2}R}& 1+\frac{h}{2C_{2}R}& \frac{h}{2C_2}\\ 0& 0& -\frac{h}{2L}& 1\end{array}\right)\left(\begin{array}{c}\phi (t_k+h)\\ v_1(t_k+h)\\ v_2(t_k+h)\\ \ell (t_k+h)\end{array}\right)\hfill \\ =\left(\begin{array}{cccc}1& \frac{h}{2}& 0& 0\\ 0& 1-\frac{h}{2C_{1}R}-\frac{h}{2C_1}({\sum }_{i=1}^2{\eta }_i(t_k)a_i)& \frac{h}{2C_{1}R}& 0\\ 0& \frac{h}{2C_{2}R}& 1-\frac{h}{2C_{2}R}& -\frac{h}{2C_2}\\ 0& 0& \frac{h}{2L}& 1\end{array}\right)\left(\begin{array}{c}\phi (t_k)\\ v_1(t_k)\\ v_2(t_k)\\ \ell (t_k)\end{array}\right),\hfill \end{array}$$

(27)

then we have

$$\left(\begin{array}{c}\phi (t_k+h)\\ v_1(t_k+h)\\ v_2(t_k+h)\\ \ell (t_k+h)\end{array}\right)=\mathrm{\Xi }\left(\begin{array}{c}\phi (t_k)\\ v_1(t_k)\\ v_2(t_k)\\ \ell (t_k)\end{array}\right),$$

(28)

where

$$\begin{array}{rcl}\mathrm{\Xi }& =& {\left(\begin{array}{cccc}1& -\frac{h}{2}& 0& 0\\ 0& 1+\frac{h}{2C_{1}R}+\frac{h}{2C_1}({\sum }_{i=1}^2{\eta }_i(t_k)a_i)& -\frac{h}{2C_{1}R}& 0\\ 0& -\frac{h}{2C_{2}R}& 1+\frac{h}{2C_{2}R}& \frac{h}{2C_2}\\ 0& 0& -\frac{h}{2L}& 1\end{array}\right)}^{-1}\\ \times \left(\begin{array}{cccc}1& \frac{h}{2}& 0& 0\\ 0& 1-\frac{h}{2C_{1}R}-\frac{h}{2C_1}({\sum }_{i=1}^2{\eta }_i(t_k)a_i)& \frac{h}{2C_{1}R}& 0\\ 0& \frac{h}{2C_{2}R}& 1-\frac{h}{2C_{2}R}& -\frac{h}{2C_2}\\ 0& 0& \frac{h}{2L}& 1\end{array}\right).\end{array}$$

(29)

Let

$$\begin{array}{rcl}\tilde{\mathrm{\Xi }}& =& {\left(\begin{array}{cccc}1& -\frac{h}{2}& 0& 0\\ 0& 1+\frac{h}{2C_{1}R}+\frac{h}{2C_1}co\{a_1,a_2\}& -\frac{h}{2C_{1}R}& 0\\ 0& -\frac{h}{2C_{2}R}& 1+\frac{h}{2C_{2}R}& \frac{h}{2C_2}\\ 0& 0& -\frac{h}{2L}& 1\end{array}\right)}^{-1}\\ \times \left(\begin{array}{cccc}1& \frac{h}{2}& 0& 0\\ 0& 1-\frac{h}{2C_{1}R}-\frac{h}{2C_1}co\{a_1,a_2\}& \frac{h}{2C_{1}R}& 0\\ 0& \frac{h}{2C_{2}R}& 1-\frac{h}{2C_{2}R}& -\frac{h}{2C_2}\\ 0& 0& \frac{h}{2L}& 1\end{array}\right),\end{array}$$

(30)

where $co\{a_1,a_2\}$ denotes the closure of the convex hull generated by the real numbers $a_1$ and $a_2$.

Obviously, by the iterative scheme (28), we can draw the conclusions of Theorems 4 and 5.

Theorem 4 If $\rho (\tilde{\mathrm{\Xi }})=1$, and the eigenvalues of $M(\tilde{\mathrm{\Xi }})=1$ only correspond to the elementary divisors of the matrix $\tilde{\mathrm{\Xi }}$, then the iterative scheme (28) is convergent, i.e., (28) converges to a fixed state, where $\rho (\tilde{\mathrm{\Xi }})$ and $M(\tilde{\mathrm{\Xi }})$ denote the spectral radius and matrix module of $\tilde{\mathrm{\Xi }}$, respectively.

Theorem 5 If $\rho (\tilde{\mathrm{\Xi }})<1$, then the iterative scheme (28) is convergent, i.e., (28) converges to a fixed state, where $\rho (\tilde{\mathrm{\Xi }})$ denotes spectral radius of the matrix $\tilde{\mathrm{\Xi }}$.

Theorem 6 If $\parallel \tilde{\mathrm{\Xi }}\parallel <1$, then the iterative scheme (28) is convergent, i.e., (28) converges to a fixed state, where $\parallel \tilde{\mathrm{\Xi }}\parallel$ denotes the norm of the matrix $\tilde{\mathrm{\Xi }}$.

Proof Since $\rho (\tilde{\mathrm{\Xi }})\le \parallel \tilde{\mathrm{\Xi }}\parallel <1$, according to Theorem 5, it follows that Theorem 6 holds. □

Remark 1 In fact, in Theorems 5 and 6, according to the theory of stability for discrete dynamical systems, we find that the iterative scheme (28) is exponentially convergent when $\rho (\tilde{\mathrm{\Xi }})<1$ or $\parallel \tilde{\mathrm{\Xi }}\parallel <1$.

4 Conclusion

The area of memristive oscillator systems is ripe with open problems and challenges, and more exploratory analyses will encourage and motivate researchers to enter this exciting field of research. In this paper, we investigate the convergence analysis of two types of algorithms for solving a class of memristive oscillator systems. Some preliminary results have been shown. We hope that such theoretical analysis in this area will contribute to further ignition of interest and promotion of multi-discipline studies.