Sufficient conditions for global exponential stability of discrete switched time-delay systems with linear fractional perturbations via switching signal design

Abstract

The switching signal design for global exponential stability of discrete switched systems with interval time-varying delay and linear fractional perturbations is considered in this paper. Some LMI stability criteria are proposed to design the switching signal and guarantee the global exponential stability for a discrete switched time-delay system. Nonnegative inequalities are introduced to improve the conservativeness of the proposed results. A procedure is provided to guarantee the stability of a switched system and design the switching signal. Finally, some numerical examples are illustrated to show the main results.

1 Introduction

A switched system is composed of a family of subsystems and a switching signal that specifies which subsystem is activated to the system trajectories at each instant of time [1]. Switched systems are often encountered in many practical examples such as automated highway systems, automotive engine control system, constrained robotics, robot manufacture, and stepper motors. Many complicate system behaviors, such as multiple limit cycles and chaos, are produced by a switching signal in systems [1–14]. It is also well known that the existence of delay in a system may cause instability or bad performance in closed control systems [15–18]. Time-delay phenomena usually appear in many practical systems such as AIDS epidemic, chemical engineering systems, hydraulic systems, population dynamic model, and rolling mill. Hence stability analysis and stabilization for discrete switched systems with time delay have been studied in recent years [2–4, 6, 7, 9, 10, 12–14].

There are three basic problems in dealing with the stability of discrete switched systems: (1) Find the stability or controller design of switched systems under an arbitrary switching signal [3, 4, 8, 9, 13]; (2) Identify the useful stabilizing switching signal for switched systems [14]; (3) Construct the stabilizing switching signal for switched systems [6, 7]. In this paper, the stability conditions for switching signal design of uncertain discrete switched time-delay systems will be developed. It is interesting to note that the stable property for each subsystem cannot imply that the overall system is also stable under an arbitrary switching signal [4]. Another interesting fact is that the stability of a switched system can be achieved by choosing a switching signal even when each subsystem is unstable [6, 7]. Although many important results have been proposed to design the switching signal of switched time-delay systems, but there are only few reports concerning the switching signal design of discrete switched time-delay systems [6, 7]. Some additional nonnegative inequalities are used to improve the conservativeness for the obtained results [4, 18]. Interval time-varying delay and linear fractional perturbations of a system are also included in our problem under consideration. In this paper, a new scheme for switching signal design is developed to guarantee global exponential stability of a switched system with interval time-varying delay and linear fractional perturbations. By the proposed approach, our results are shown to be less conservative than some recent reports in our demonstrated numerical examples.

The notation used throughout this paper is as follows. For a matrix A, we denote the transpose by $A^T$, symmetric positive (negative) definite by $A>0$ ($A<0$), maximal eigenvalue by ${\lambda }_{max}(A)$, minimal eigenvalue by ${\lambda }_{min}(A)$, $n\times m$ dimension by $A_{(n\times m)}$. $A\le B$ means that matrix $B-A$ is symmetric positive semi-definite. I denotes the identity matrix. For a vector x, we denote the Euclidean norm by $\parallel x\parallel$. Define $\overline{N}=\{1,2,\dots ,N\}$, $A\setminus B=\{x|x\in A\text{ and }x\notin B\}$, ${\parallel x_k\parallel }_s={max}_{\theta =-r_M,-r_M+1,\dots ,0}\parallel x(k+\theta )\parallel$.

2 Problem statement and preliminaries

Consider the following uncertain discrete switched time-delay system:

(1a)

(1b)

where $x(k)\in {\mathrm{\Re }}^n$, $x_k$ is the state defined by $x_k(\theta ):=x(k+\theta )$, $\mathrm{\forall }\theta \in \{-r_M,-r_M+1,\dots ,0\}$, σ is a switching signal in the finite set $\{1,2,\dots ,N\}$ and will be chosen to preserve the stability of the system, $\varphi (k)\in {\mathrm{\Re }}^n$ is an initial state function, time-varying delay $r(k)$ is a function from $\{0,1,2,3,\dots \}$ to $\{0,1,2,3,\dots \}$ and $1\le r_m\le r(k)\le r_M$, $r_m$ and $r_M$ are two given positive integers. Matrices $A_i,B_i\in {\mathrm{\Re }}^{n\times n}$, $i=1,2,\dots ,N$, are constant. $\mathrm{\Delta }{A}_i(k)$ and $\mathrm{\Delta }{B}_i(k)$ are two perturbed matrices satisfying the following condition:

(1c)

(1d)

where $M_i$, $N_{Ai}$, and $N_{Bi}$, $i=1,2,\dots ,N$, and ${\mathrm{\Xi }}_i$ are some given constant matrices with appropriate dimensions. ${\mathrm{\Gamma }}_i(k)$ is an unknown matrix representing the perturbation which satisfies

$${\mathrm{\Gamma }}_i^T(k){\mathrm{\Gamma }}_i(k)\le I.$$

(1e)

Definition 1 System (1a)-(1e) is said to be globally exponentially stable with a convergence rate α if there are two positive constants $0<\alpha <1$ and Ψ such that

$$\parallel x(k)\parallel \le \mathrm{\Psi }\cdot {\parallel x_0\parallel }_s\cdot {\alpha }^k,k=0,1,2,3,\dots .$$

Define the switching domains of a switching signal by

$${\mathrm{\Omega }}_i(\alpha ,P,U_i,A_i)=\{x(k)\in {\mathrm{\Re }}^n:x^T(k)(A_i^{T}P{A}_i-{\alpha }^2\cdot U_i)x(k)<0\},i=1,2,\dots ,N,$$

(2a)

where the constant $0<\alpha <1$ is a convergence rate, matrices $P>0$, $U_i>0$ are given from the proposed results, and

$$\begin{array}{r}{\overline{\mathrm{\Omega }}}_1={\mathrm{\Omega }}_1,{\overline{\mathrm{\Omega }}}_2={\mathrm{\Omega }}_2\setminus {\overline{\mathrm{\Omega }}}_1,{\overline{\mathrm{\Omega }}}_3={\mathrm{\Omega }}_3\setminus {\overline{\mathrm{\Omega }}}_1\setminus {\overline{\mathrm{\Omega }}}_2,\dots ,\\ {\overline{\mathrm{\Omega }}}_N={\mathrm{\Omega }}_N\setminus {\overline{\mathrm{\Omega }}}_1\setminus \cdots \setminus {\overline{\mathrm{\Omega }}}_{N-1}.\end{array}$$

(2b)

Now the main results are provided in the following theorem.

Theorem 1 If for some constants $0<\alpha <1$, $0\le {\alpha }_i\le 1$, $i\in \overline{N}$, and ${\sum }_{i=1}^N{\alpha }_i=1$, there exist some $n\times n$ matrices $P>0$, $Q>0$, $R_1>0$, $R_2>0$, $R_3>0$, $S>0$, $T>0$, $U_i>0$, $i\in \overline{N}$, $V_{l11}\in {\mathrm{\Re }}^{4n\times 4n}$, $V_{l12}\in {\mathrm{\Re }}^{4n\times n}$, $V_{l22}\in {\mathrm{\Re }}^{n\times n}$, $l=1,2,3,4$, and constants ${\epsilon }_i>0$, $i\in \overline{N}$, such that the following LMI conditions hold for all $j=1,2,\dots ,N$:

(3a)

(3b)

(3c)

(3d)

where

Then system (1a)-(1e) is globally exponentially stable with the convergence rate $0<\alpha <1$ by the switching signal designed by

$$\sigma (k,x(k))=i,\mathit{\text{whenever}}x(k)\in {\overline{\mathrm{\Omega }}}_i,$$

(3e)

where ${\overline{\mathrm{\Omega }}}_i$ is defined in (2a), (2b).

Proof

Define the Lyapunov functional

$$\begin{array}{rcl}V(x_k)& =& {\alpha }^{-2k}{x}^T(k)Px(k)+\sum _{i=k-r(k)}^{k-1}{\alpha }^{-2i}{x}^T(i)Qx(i)+\sum _{j=-r_M+1}^{-r_m}\sum _{i=k+j}^{k-1}{\alpha }^{-2i}{x}^T(i)Qx(i)\\ +\sum _{j=-r_M+1}^0\sum _{i=k-1+j}^{k-1}{\alpha }^{-2i}{y}^T(i)[R_1+R_2]y(i)+\sum _{j=-r_m+1}^0\sum _{i=k-1+j}^{k-1}{\alpha }^{-2i}{y}^T(i)R_{3}y(i)\\ +\sum _{i=k-r_M}^{k-1-r_m}{\alpha }^{-2i}{x}^T(i)Sx(i)+\sum _{i=k-r_m}^{k-1}{\alpha }^{-2i}{x}^T(i)Tx(i),\end{array}$$

(4)

where $P>0$, $Q>0$, $R_1>0$, $R_2>0$, $R_3>0$, $S>0$, $T>0$, and $y(i)=x(i+1)-x(i)$. The forward difference of Lyapunov functional (4) along the solutions of system (1a)-(1e) has the form

$$\begin{array}{rcl}\mathrm{\Delta }V(x_k)& =& V(x_{k+1})-V(x_k)\\ =& {\alpha }^{-2k}\cdot [{\alpha }^{-2}\cdot x^T(k+1)Px(k+1)-x^T(k)Px(k)]\\ +\sum _{i=k+1-r(k+1)}^k{\alpha }^{-2i}{x}^T(i)Qx(i)-\sum _{i=k-r(k)}^{k-1}{\alpha }^{-2i}{x}^T(i)Qx(i)\\ +{\alpha }^{-2k}\cdot (r_M-r_m)\cdot x^T(k)Qx(k)-\sum _{i=k+1-r_M}^{k-r_m}{\alpha }^{-2i}{x}^T(i)Qx(i)\\ +{\alpha }^{-2k}\cdot r_M\cdot y^T(k)[R_1+R_2]y(k)-\sum _{i=k-r_M}^{k-1}{\alpha }^{-2i}{y}^T(i)[R_1+R_2]y(i)\\ +{\alpha }^{-2k}\cdot r_m\cdot y^T(k)R_{3}y(k)-\sum _{i=k-r_m}^{k-1}{\alpha }^{-2i}{y}^T(i)R_{3}y(i)\\ +{\alpha }^{-2k}\cdot [{\alpha }^{2r_m}\cdot x^T(k-r_m)Sx(k-r_m)-{\alpha }^{2r_M}\cdot x^T(k-r_M)Sx(k-r_M)]\\ +{\alpha }^{-2k}\cdot [x^T(k)Tx(k)-{\alpha }^{2r_m}\cdot x^T(k-r_m)Tx(k-r_m)].\end{array}$$

(5a)

By some simple derivations, we have

From the above derivation, we can obtain the following result:

$$\begin{array}{rcl}\mathrm{\Delta }V(x_k)& =& V(x_{k+1})-V(x_k)\\ \le & {\alpha }^{-2k}\cdot \{{\alpha }^{-2}\cdot x^T(k+1)Px(k+1)-x^T(k)[P-T]x(k)\\ +x^T(k)[(r_M-r_m+1)\cdot Q]x(k)-{\alpha }^{2r_M}\cdot x^T(k-r(k))Qx(k-r(k))\\ +{[x(k+1)-x(k)]}^T[r_M\cdot (R_1+R_2)+r_m\cdot R_3][x(k+1)-x(k)]\\ -{\alpha }^{2r_M}\cdot [\sum _{i=k-r(k)}^{k-1}{y}^T(i)R_{1}y(i)+\sum _{i=k-r_M}^{k-r(k)-1}{y}^T(i)R_{1}y(i)+\sum _{i=k-r_M}^{k-1}{y}^T(i)R_{2}y(i)]\\ -{\alpha }^{2r_m}\cdot [\sum _{i=k-r_m}^{k-1}{y}^T(i)R_{3}y(i)]-{\alpha }^{2r_m}\cdot x^T(k-r_m)[T-S]x(k-r_m)\\ -{\alpha }^{2r_M}\cdot x^T(k-r_M)Sx(k-r_M)\}.\end{array}$$

(5b)

Define

$$X^T(k)=\left[\begin{array}{cccc}{x}^T(k)& x^T(k-r(k))& x^T(k-r_M)& x^T(k-r_m)\end{array}\right].$$

By system (1a)-(1e), LMIs in (3b), and ${\sum }_{i=k-r(k)}^{k-1}y(i)=x(k)-x(k-r(k))$, we have

(6a)

(6b)

(6c)

(6d)

Assume $\sigma (k,x(k))=j\in \overline{N}$, then we can obtain the following result from system (1a)-(1e):

and

(7a)

where

(7b)

Define

$${\overline{\mathrm{\Sigma }}}_j=\left[\begin{array}{cc}{\overline{\mathrm{\Sigma }}}_{1j}& {\overline{\mathrm{\Sigma }}}_{2j}\\ \ast & {\mathrm{\Sigma }}_{3j}\end{array}\right]=\left[\begin{array}{cc}{\overline{\mathrm{\Sigma }}}_{1j}& {\mathrm{\Sigma }}_{2j}\\ \ast & {\mathrm{\Sigma }}_{3j}\end{array}\right]+{\mathrm{\Gamma }}_j{\mathrm{\Delta }}_j(k){\mathrm{\Omega }}_j^T+{\mathrm{\Omega }}_j{\mathrm{\Delta }}_j^T(k){\mathrm{\Gamma }}_j^T,$$

(7c)

where

By condition (3d) with Lemma 1 and the switching signal defined in (3e), we can obtain the following result:

$$x^T(k)({\alpha }^{-2}{A}_j^{T}P{A}_j-U_i)x(k)\le 0,\mathrm{\forall }x(k)\in {\overline{\mathrm{\Omega }}}_j.$$

(7d)

By Lemmas 2 and 3, the condition ${\overline{\overline{\mathrm{\Sigma }}}}_j<0$ in (3c) will imply ${\overline{\mathrm{\Sigma }}}_j<0$ in (7c). ${\overline{\mathrm{\Sigma }}}_j<0$ in (7c) will also imply ${\mathrm{\Sigma }}_j<0$ in (7b). From the condition (7d) and ${\mathrm{\Sigma }}_j<0$ in (7b) with (3a) and (3b), we have

This implies

where

$$\begin{array}{rcl}{\delta }_1& =& {\lambda }_{max}(P)+[r_M+r_M(r_M-r_m)]\cdot {\lambda }_{max}(Q)+r_M^2\cdot {\lambda }_{max}(R_1+R_2)+r_m^2\cdot {\lambda }_{max}(R_3)\\ +(r_M-r_m)\cdot {\lambda }_{max}(S)+r_m\cdot {\lambda }_{max}(T).\end{array}$$

By some simple derivations, we have

$$\parallel x(k)\parallel \le \sqrt{{\delta }_1/{\lambda }_{min}(P)}\cdot {\alpha }^k\cdot {\parallel x_0\parallel }_s,k=0,1,2,3,\dots .$$

By Definition 1, system (1a)-(1e) is globally exponentially stable with the convergence rate $0<\alpha <1$ with the switching signal in (3e). This completes this proof. □

Remark 1

Consider the discrete linear switched system:

$$x(k+1)=A_{\sigma }x(k).$$

Now we can choose the Lyapunov function as $V(x_k)={\alpha }^{-2k}{x}^T(k)Px(k)$ with matrix $P>0$, the forward difference of the Lyapunov function is given by

$$\mathrm{\Delta }V(x_k)=V(x_{k+1})-V(x_k)={\alpha }^{-2k}\cdot [{\alpha }^{-2}\cdot x^T(k+1)Px(k+1)-x^T(k)Px(k)].$$

With $\sigma (k,x(k))=j\in \overline{N}$, we have

$$x(k+1)=A_{j}x(k),$$

and

$$\mathrm{\Delta }V(x_k)={\alpha }^{-2k}\cdot x^T(k)[{\alpha }^{-2}\cdot A_j^{T}P{A}_j-U_j+U_j-P]x(k),$$

where matrix $U_i$ satisfies $U_i>0$ and $U_i-P<0$. If the condition in Lemma 1 is satisfied, then we can obtain the following two results:

In order to achieve the exponential stability of a discrete switched system, the condition in Lemma 1 will be a reasonable choice and a feasible setting.

Remark 2 The matrix uncertainties in (1c)-(1e) are usually called linear fractional perturbations [16]. The parametric perturbations in [4, 9, 10] are the special conditions of the considered perturbations with ${\mathrm{\Xi }}_i=0$, $i\in \underline{N}$.

Remark 3 Under the same switching signal defined in (3e), the switching domains of [6, 7] are selected as:

$${\mathrm{\Omega }}_i(P,U,A_i)=\{x(k)\in R^n:x^T(k)[(r_M-r_m)\cdot U-A_i^{T}P-P{A}_i]x(k)<0\},i=1,2,\dots ,N,$$

where matrices $P>0$ and $U>0$. It is noted that above selections are similar to switching signal design in continuous switched systems [8]. Hence the proposed switching domain design approach is the discrete version of [6, 7] and shown to be useful from numerical simulations.

In what follows, we consider the non-switched uncertain discrete time-delay system:

(8a)

(8b)

where $\varphi (k)\in {\mathrm{\Re }}^n$ is an initial state function, time-varying delay $r(k)$ is a function from $\{0,1,2,3,\dots \}$ to $\{0,1,2,3,\dots \}$ and $1\le r_m\le r(k)\le r_M$, $r_m$ and $r_M$ are two given positive integers. Matrices $A,B\in {\mathrm{\Re }}^{n\times n}$ are constant. $\mathrm{\Delta }A(k)$ and $\mathrm{\Delta }B(k)$ are two perturbed matrices satisfying the following condition:

(8c)

(8d)

where M, $N_A$, and $N_B$, and Ξ are some given constant matrices with appropriate dimensions. $\mathrm{\Gamma }(k)$ is an unknown matrix representing the perturbation which satisfies

$${\mathrm{\Gamma }}^T(k)\mathrm{\Gamma }(k)\le I.$$

(8e)

The following sufficient conditions for the stability of system (8a)-(8e) can be obtained in a similar way to Theorem 1.

Theorem 2 If a given constant $0<\alpha <1$, there exist some $n\times n$ matrices $P>0$, $Q>0$, $R_1>0$, $R_2>0$, $R_3>0$, $S>0$, $T>0$, $V_{l11}\in {\mathrm{\Re }}^{4n\times 4n}$, $V_{l12}\in {\mathrm{\Re }}^{4n\times n}$, $V_{l22}\in {\mathrm{\Re }}^{n\times n}$, $l=1,2,3,4$, and constants $\epsilon >0$ such that (3a), (3b), and the following LMI conditions are satisfied:

$$\overline{\overline{\mathrm{\Sigma }}}=\left[\begin{array}{cccccccc}{\mathrm{\Sigma }}_{11}& 0& 0& 0& {\mathrm{\Sigma }}_{15}& {\mathrm{\Sigma }}_{16}& 0& {\mathrm{\Sigma }}_{18}\\ \ast & {\mathrm{\Sigma }}_{22}& 0& 0& {\mathrm{\Sigma }}_{25}& {\mathrm{\Sigma }}_{26}& 0& {\mathrm{\Sigma }}_{28}\\ \ast & \ast & {\mathrm{\Sigma }}_{33}& 0& 0& 0& 0& 0\\ \ast & \ast & \ast & {\mathrm{\Sigma }}_{44}& 0& 0& 0& 0\\ \ast & \ast & \ast & \ast & {\mathrm{\Sigma }}_{55}& 0& {\mathrm{\Sigma }}_{57}& 0\\ \ast & \ast & \ast & \ast & \ast & {\mathrm{\Sigma }}_{66}& {\mathrm{\Sigma }}_{67}& 0\\ \ast & \ast & \ast & \ast & \ast & \ast & {\mathrm{\Sigma }}_{77}& {\mathrm{\Sigma }}_{78}\\ \ast & \ast & \ast & \ast & \ast & \ast & \ast & {\mathrm{\Sigma }}_{88}\end{array}\right]+\left[\begin{array}{cc}{\mathrm{\Omega }}_{(4n\times 4n)}& 0_{(4n\times 4n)}\\ \ast & 0_{(4n\times 4n)}\end{array}\right]<0,$$

where

Then system (8a)-(8e) is globally exponentially stable with the convergence rate $0<\alpha <1$.

Remark 4 In Theorems 1 and 2, the global asymptotic stability of switched system (1a)-(1e) and non-switched system (8a)-(8e) can be achieved by setting $\alpha =1$. The nonnegative inequalities in (6a)-(6d) are used to improve the conservativeness of the obtained results.

Remark 5 If we wish to select a switching signal to guarantee the stability of switched system (1a)-(1e), the following procedures are proposed.

Step 1 Test the exponential stability of each subsystem of switched system (1a)-(1e) by Theorem 2 with $A=A_i$, $B=B_i$, $M=M_i$, $N_A=N_{Ai}$, $N_B=N_{Bi}$, $\mathrm{\Xi }={\mathrm{\Xi }}_i$, $i=1,2,\dots ,N$. If the sufficient conditions in Theorem 2 have a feasible solution for some $i\in \underline{N}$, the switching signal is selected by $\sigma =i$ and the stability of the switched system in (1a)-(1e) can be guaranteed.

Step 2 If the obtained stability results for each subsystem of switched time-delay system (1a)-(1e) do not satisfy the requirement in Step 1, we can use Theorem 1 to design the switching signal to guarantee the global exponential stability of switched time-delay system (1a)-(1e).

From the results in Steps 1-2, we can propose a less conservative stability result of the system.

3 Illustrative examples

Example 1 Consider system (1a)-(1e) with no perturbations and the following parameters (Example 3.1 of [6]):

$$\begin{array}{r}{A}_1=\left[\begin{array}{cc}0.54& 1.02\\ -0.17& -0.31\end{array}\right],A_2=\left[\begin{array}{cc}-0.01& -0.06\\ 0.01& 0.04\end{array}\right],\\ B_1=\left[\begin{array}{cc}0.18& 0.36\\ -0.06& -0.12\end{array}\right],B_2=\left[\begin{array}{cc}0.11& 0.18\\ -0.03& -0.04\end{array}\right].\end{array}$$

(9)

In order to show the obtained results, the allowable delay upper bounds and switching laws in (2a), (2b) that guarantee the global asymptotic and exponential stability for system (1a)-(1e) with (9) are provided in Table 1.

Table 1 The obtained results for our proposed results in this paper

Example 2 Consider system (1a)-(1e) with the following parameters (Example 1 of [10]):

$$\begin{array}{r}{A}_1=\left[\begin{array}{cc}0.8& 0.2\\ 0& 0.91\end{array}\right],A_2=\left[\begin{array}{cc}0.3& 0\\ 0& 0.58\end{array}\right],B_1=\left[\begin{array}{cc}-0.1& 0\\ -0.1& -0.1\end{array}\right],\\ B_2=\left[\begin{array}{cc}0.12& 0\\ 0.11& 0.11\end{array}\right],M_1=M_2=\left[\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right],\\ N_{A1}=N_{A2}=N_{B1}=N_{B2}=\left[\begin{array}{cc}0.01& 0\\ 0& 0.01\end{array}\right],{\mathrm{\Xi }}_1={\mathrm{\Xi }}_2=0.\end{array}$$

(10)

The delay upper bounds and switching signals (3e) with stability domains in (2a), (2b) that guarantee the global asymptotic stability for system (1a)-(1e) with (10) are provided in Table 2.

Table 2 Some obtained results for our proposed results in this paper

Example 3 Consider system (1a)-(1e) with the following parameters:

$$\begin{array}{r}{A}_1=\left[\begin{array}{cc}1.02& 0.1\\ 0& 0.05\end{array}\right],A_2=\left[\begin{array}{cc}0.1& 0\\ 0.1& 1.01\end{array}\right],B_1=\left[\begin{array}{cc}0& 0\\ 0.1& -0.1\end{array}\right],\\ B_2=\left[\begin{array}{cc}-0.1& 0\\ 0.1& -0.1\end{array}\right],M_1=M_2=\left[\begin{array}{cc}0.2& 0\\ 0& 0.1\end{array}\right],\\ N_{A1}=N_{A2}=N_{B1}=N_{B2}=\left[\begin{array}{cc}0.01& 0\\ 0& 0.02\end{array}\right],{\mathrm{\Xi }}_1={\mathrm{\Xi }}_2=0.1\cdot I.\end{array}$$

(11)

The delay upper bounds and switching signals (3e) with stability domains in (2a), (2b) that guarantee the global asymptotic stability for system (1a)-(1e) with (11) are provided in Table 3.

Table 3 The obtained results for our proposed results in this paper

Note that the matrices $A_1$ and $A_2$ in this example are not Hurwitz, the results in [4, 6, 7], and [10] cannot find any feasible solution to guarantee the stability of a switched system for arbitrary and designed switching signals. The proposed results in [4] and [10] are subjected to an arbitrary switching signal condition, we illustrate the comparisons here only for showing the advantage for switching signal design of the proposed results in this paper.

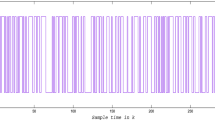
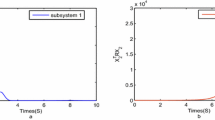
Switched system (1a)-(1e) with (11) is asymptotically stable by the switching signal designed by

$$\sigma (k,x(k))=\{\begin{array}{cc}1,\hfill & x(k)\in {\overline{\mathrm{\Omega }}}_1,\hfill \\ 2,\hfill & x(k)\in {\mathrm{\Re }}^2\setminus {\overline{\mathrm{\Omega }}}_1,\hfill \end{array}$$

(12)

where

$${\overline{\mathrm{\Omega }}}_1=\{{[\begin{array}{cc}{x}_1& x_2\end{array}]}^T\in {\mathrm{\Re }}^2:27.9396x_1^2+3.3182x_1{x}_2-18.2592x_2^2\le 0\}.$$

With initial state $\varphi (\theta )={[10-10]}^T$, $\theta =-7,-6,\dots ,-1,0$, state trajectories for the selected switching signal in (12) and the arbitrary switching signal are shown in Figure 1 and Figure 2, respectively.

Figure 1

State trajectories for the selected switching signal in ( 12 ) (solid line: ${\mathit{x}}_{\mathbf{1}}$ , dotted line:  ${\mathit{x}}_{\mathbf{2}}$ ).

Figure 2

State trajectories for the arbitrary switching signal (solid line: ${\mathit{x}}_{\mathbf{1}}$ , dotted line: ${\mathit{x}}_{\mathbf{2}}$ ).

Example 4 Consider system (1a)-(1e) with no perturbations and the following parameters (Example 1 of [7]):

$$\begin{array}{r}{A}_1=\left[\begin{array}{cc}-0.1& 0.01\\ 0.02& -0.2\end{array}\right],A_2=\left[\begin{array}{cc}1& 0.2\\ 0.1& 2\end{array}\right],\\ B_1=\left[\begin{array}{cc}-0.1& 0.01\\ 0.02& -0.3\end{array}\right],B_2=\left[\begin{array}{cc}0.1& 0.02\\ 0.01& 0.2\end{array}\right].\end{array}$$

(13)

The delay upper bounds and switching signals (3e) with stability domains in (2a), (2b) that guarantee the global asymptotic stability for system (1a)-(1e) with (13) are provided in Table 4.

Table 4 The obtained results for our proposed results in this paper

Note that the eigenvalues of $A_2$ are 0.9804 and 2.0196, Theorem 1 and Theorem 2 with the second subsystem cannot use to guarantee the stability of system (1a)-(1e) with (13).

4 Conclusion

In this paper, the switching signal design to guarantee the global exponential stability for uncertain discrete switched systems with interval time-varying delay and linear fractional perturbations has been considered. Some nonnegative inequalities and LMI approach are used to improve the conservativeness of the proposed results. A procedure has been proposed to test the stability of the switched system and design the switching signal. The obtained results are shown to be less conservative and useful via numerical examples. In the future, switching signal designs for robust stabilization and performance (guaranteed cost control, $H_{\mathrm{\infty }}$ control, nonfragile control, passivity analysis and passive control) can be investigated and developed [10, 19, 20].

Appendix

Lemma 1 If there exist some constants $0<\alpha <1$, $0\le {\alpha }_i\le 1$, $i\in \underline{N}$, ${\sum }_{i=1}^N{\alpha }_i=1$, some matrices $P>0$, $U_i>0$ such that

$$\sum _{i=1}^N{\alpha }_i\cdot (A_i^{T}P{A}_i-{\alpha }^2\cdot U_i)<0,$$

we have

$$\bigcup _{i=1}^N{\overline{\mathrm{\Omega }}}_i={\mathrm{\Re }}^n\mathit{\text{and}}{\overline{\mathrm{\Omega }}}_i\cap {\overline{\mathrm{\Omega }}}_j=\mathrm{\Phi },\mathrm{\forall }i\ne j,$$

where Φ is an empty set of ${\mathrm{\Re }}^n$ and ${\overline{\mathrm{\Omega }}}_i$ is defined in (2a), (2b).

Proof This lemma can be proved in a similar way to [6–8]. □

Lemma 2 [21]

For a given matrix $S=\left[\begin{array}{cc}{S}_{11}& S_{12}\\ 2\ast & S_{22}\end{array}\right]$ with $S_{11}=S_{11}^T$, $S_{22}=S_{22}^T$, the following conditions are equivalent:

• (1) $S<0$,

• (2) $S_{22}<0$, $S_{11}-S_{12}{S}_{22}^{-1}{S}_{12}^T<0$.

Lemma 3 [16]

Suppose that ${\mathrm{\Delta }}_i(k)$ is defined in (1d) and satisfies (1e), then for real matrices $V_i$, $W_i$, and $X_i$ with $X_i=X_i^T$, the following statements are equivalent:

• (I) The inequality is satisfied

  $$X_i+V_i{\mathrm{\Delta }}_i(k)W_i+W_i^T{\mathrm{\Delta }}_i^T(k)V_i^T<0;$$

• (II) There exists a scalar ${\epsilon }_i>0$ such that

  $$\left[\begin{array}{ccc}{X}_i& V_i& {\epsilon }_i\cdot W_i^T\\ \ast & -{\epsilon }_i\cdot I& {\epsilon }_i\cdot {\mathrm{\Xi }}_i^T\\ \ast & \ast & -{\epsilon }_i\cdot I\end{array}\right]<0,$$

where the matrix ${\mathrm{\Xi }}_i$ is defined in (1d).