Abstract
This paper deals with the reliable control problem of positive switched systems with time-varying delays. Under the case where both stable and unstable subsystems coexist, sufficient conditions are proposed to guarantee the exponential stability of positive switched systems with time-varying delays, and the average dwell time approach is utilized for the stability analysis. The result is also extended to solve the reliable control problem. All the results are formulated in a set of linear matrix inequalities (LMIs), which can be easily verified or implemented. The obtained theoretical results are demonstrated by a numerical example.
Similar content being viewed by others
1 Introduction
Switched systems, a type of hybrid dynamical systems, are composed of a number of subsystems and a switching signal which defines a specific subsystem being activated during a certain interval. Many real-world systems such as mechanical systems, automotive industry, aircraft and air traffic control systems as well as chemical processes can be modeled as such systems [1–3].
Very recently, positive switched systems, whose states and outputs are nonnegative whenever the initial conditions and inputs are nonnegative, have been highlighted and investigated by many researchers due to their broad applications in communication systems [4, 5], viral mutation dynamics under drug treatment [6], formation flying [7] and system theory [8–12], to mention a few. So far, many useful results for positive switched systems have been obtained in the literature, particularly with respect to the stability analysis [13–16]. However, it should be noted that, although many recent control engineering and mathematics works on switched systems have appeared [17, 18], there are still many open questions relating to positive switched systems.
In practice, time delay phenomenon is frequently encountered in engineering and social systems, and the existence of it may cause undesirable performance in feedback systems such as chaos [19, 20]. Therefore, many results have been reported for time-delay systems [21–24] over the past years, but not until recently have the positive switched systems with time delays become a topic of major interest.
On the other hand, the popularity of studying a reliable control problem is raised for the growing demands of system reliability in aerospace and industrial process. When controlling a real plant with failures of control components, classical control methods may not achieve satisfactory performance. To overcome this problem, reliable control has made great progress recently. Among the existing studies, the problem of robust reliable control for uncertain switched nonlinear systems with time delays is addressed in [25], and a reliable control method for uncertain switched systems with time-varying delays and actuators faults is presented in [26]. It should be pointed out that the aforementioned results are based on a basic assumption that the subsystems are all stable. Due to the fact that unstable subsystems cannot be avoided in many applications, the reliable stabilization problems for switched systems with faulty actuators are solved in [27–29] under the restrictions that not all subsystems are stable. However, to the best of our knowledge, the issue of reliable control for positive switched systems with stable and unstable subsystems has not been fully investigated, which motivates us to carry out the present work.
In this paper, we focus our attention on the reliable control problem of positive switched delayed systems with both stable and unstable subsystems. The main contribution of this paper lies in three aspects. Firstly, by using the average dwell time approach, stability conditions are proposed for positive switched delayed systems with both stable and unstable subsystems. Secondly, -gain performance analysis for the underlying systems is developed. Thirdly, a reliable controller is derived to guarantee the exponential stability with -gain property of the resulting closed-loop systems.
The remainder of this paper is organized as follows. In Section 2, the necessary definitions and lemmas are reviewed. Section 3 is devoted to deriving the results on stability, -gain property analysis and controller design. An example is provided to illustrate the feasibility of the obtained results in Section 4. Concluding remarks are given in Section 5.
Notations In this paper, (⪯0) means that all entries of matrix A are non-negative (non-positive); (≺0) means that all entries of A are positive (negative); () means that (); denotes the transpose of matrix A; R () is the set of all real (positive real) scalars; () is an n-dimensional real (positive) vector space. The notation , where is the l th element of .
2 Problem statements and preliminaries
Consider the following switched linear systems with time-varying delays:
where and denote the state and controlled output, respectively; is the disturbance input; is the switching signal with N being the number of subsystems; , , , and , , are constant matrices with appropriate dimensions; is a vector-valued initial function defined on the interval , ; is the initial time, and denotes the k th switching instant; denotes the time-varying delay satisfying , for known constants τ and d.
Assumption 1 The exogenous noise signal is time-varying and , that is,
Next, we will give the positive definition for switched system (1).
Definition 1 System (1) is said to be positive if, for any initial conditions , , and any switching signals , the corresponding state trajectory and controlled output hold for all .
Definition 2[30]
A is called a Metzler matrix, if the off-diagonal entries of matrix A are non-negative.
The following lemma can be obtained from Lemma 3 in [14] and Proposition 1 in [13].
Lemma 1 System (1) is positive if and only if, , are Metzler matrices and, , , , .
Definition 3[31]
System (1) is said to be exponentially stable under a switching signal if for the initial condition , , there exist constants , such that the solution of the system satisfies , , where .
Definition 4[32]
For a switching signal and , let denote the switching number of over the interval . For given , , if the inequality
holds, then is called the average dwell time and is the chattering bound.
As commonly used in the literature, we choose in this paper.
Definition 5[33]
System (1) is said to have -gain performance index γ under a switching signal , if the following conditions are satisfied:
-
(i)
System (1) is exponentially stable when ;
-
(ii)
Under zero initial conditions, i.e., , , the following inequality holds for all nonzero :
(2)
Remark 1 In Definition 5, index γ characterizes the disturbance attenuation performance. The smaller γ is, the better the performance is.
When the control input with actuator failures is considered, system (1) can be written as
where , , ; is the control input with actuator failures. Actuator failures are assumed to occur within a prescribed subset of control input channel. We classify actuators of system (3) into two groups. One is a set of actuators susceptible to failures, denoted by . The other is a set of actuators robust to failures, denoted by , i.e., the complementary set of M. , , , , and , , are constant matrices with appropriate dimensions. According to the classification of actuators, we have the decomposition , , where and are formed from corresponding to M and , respectively.
Assume that the actuator faults are modeled as whose elements correspond to the set of faulty actuators M. Denote , where can be considered as a new disturbance input vector. System (3) with the following state feedback control law:
becomes
where , , , .
The purpose of this paper is: (1) to find a switching signal under which positive switched system (1) is exponentially stable with -gain performance; (2) to design a state feedback controller for positive switched system (3) such that resulting closed-loop system (5) is exponentially stable and has -gain performance index γ.
3 Main results
3.1 Stability analysis
In this section, two necessary lemmas are given firstly for the following non-switched positive system:
where A is a Metzler constant matrix and is a constant matrix; denotes the time-varying delay satisfying , ; .
Choose the co-positive type Lyapunov-Krasovskii functional candidate for system (6) as follows:
where

and , .
For the sake of simplicity, is written as in this paper.
Lemma 2 For a given positive constant α, if there exist vectorsandsuch that


where

with () represents the rth column vector of matrix A (), and, , , , represents the rth element of the vector. Then along the trajectory of system (6), we have
Proof Along the trajectory of system (6), for the co-positive type Lyapunov-Krasovskii functional (7), we have

Using the Leibniz-Newton formula, one has
Considering that
the following relationship can be obtained for any vector :
From (10) and (13), we have
One can obtain from (8) and (9) that




It follows that
Then, along the trajectory of system (6), we have
□
Lemma 3 Consider system (6), for a given positive constant β, if there exist vectorsandsuch that


where

() represents the rth column vector of matrix A (); and, , , . Then, along the trajectory of system (6), we have
Proof Choose the following co-positive type Lyapunov-Krasovskii functional candidate for system (6):
where

and , .
The rest of the proof of this lemma is similar to that of Lemma 2, and thus is omitted here. □
Now we are in a position to provide the stability conditions for the following positive switched system:
where , , are Metzler constant matrices and , , are constant matrices; denotes the time-varying delay satisfying , ; .
Let Q denote the index set of all stable subsystems, which is a nonempty subset of , and denote the index set of all unstable subsystems. Let denote the total activation time of the unstable subsystems during , let denote the total activation time of the stable subsystems during , then we have the following result.
Theorem 1 Given positive constants α and β, if there existand, , such that




where

() represents the rth column vector of matrix (), ; and, , , . Then system (21) is exponentially stable for any switching signalswith the average dwell time
where, andsatisfies
Proof
Choose the following piecewise co-positive type Lyapunov-Krasovskii functional candidate:
Let denote the switching instants of over the interval . By Lemmas 2 and 3, one can obtain from (22)-(25) that
From (27) and the co-positive type Lyapunov-Krasovskii functional, at the switching instants , , it is obtained that
where .
By (26), (28), (29) and Definition 4, for , it is not hard to get
Denoting yields
Denote

and , then
From (30)-(32), we obtain

Thus, by denoting , , it can be seen from (33) that , , where . Therefore, we can conclude that system (21) is exponentially stable for any switching signal with average dwell time (26). □
Remark 2 In Theorem 1, sufficient conditions for the existence of the exponential stability for positive switched system (21) with both stable and unstable subsystems are presented via the average dwell time approach. It is shown by (26) that when the average dwell time is sufficiently large and the total activation time of unstable subsystems is relatively small compared with that of stable subsystems, the stability of the system can be guaranteed.
3.2 -gain property analysis
Theorem 2 Given positive constants α, β and γ, if there existand, , such that




where

represents the rth column vector of matrix, . Then system (1) is exponentially stable and has-gain performance index γ for any switching signalwith the average dwell time (26).
Proof It is easy to get that (22)-(25) can be deduced from (34)-(37). According to Theorem 1, system (1) with is exponentially stable. In the sequel, we will prove that the -gain performance of system (1) is guaranteed.
Let denote the switching instants of over the interval . Following the proof line of Theorem 1, one can obtain from (34)-(37) that
where .
Then, for , we have
Under the zero initial condition, we have , then (39) becomes
From the condition (26), it is obvious that
then
That is,
Multiplying both sides of (40) by yields
By Definition 4 and condition (26), one can obtain
Integrating both sides of (42) from to ∞ leads to
This means that system (1) achieves -gain performance index γ.
The proof is completed. □
3.3 Reliable control
In what follows, we design a state feedback controller for positive switched system (3) such that resulting closed-loop system (5) is exponentially stable with -gain performance index γ.
Theorem 3 Consider system (3), for given positive constants α, β and γ, if there existand, , such that




where

() represents the rth column vector of matrix (), ; () represents the rth column vector of matrix (); , .
Then, under the controller (4), resulting closed-loop system (5) is exponentially stable and has-gain performance index γ for any switching signalswith the average dwell time (26).
Proof Under the controller (4), the resulting closed-loop system can be written as (5).
Denote , , and , , then by Theorem 2, one can obtain from (43)-(46) that closed-loop system (5) is exponentially stable and has -gain performance index γ. This completes the proof. □
We now present the following algorithm for the construction of the reliable state feedback controller.
Algorithm 1 Step 1. Input the matrices , , , , and , ;
Step 2. By adjusting parameters α and β, we can find the solutions of , , , , such that (43) and (45) hold;
Step 3. From and , one can obtain the gain matrices , and then substitute into (44) and (46). If inequalities (44) and (46) hold and are Metzler matrices, then go to Step 4; otherwise, go back to Step 2;
Step 4. With , , , the switching signal can be obtained by (26) and (27);
Step 5. Construct the feedback controller (4), where are gain matrices obtained in Step 3.
4 Numerical example
Consider positive switched system (3) with the following parameters:

By Lemma 1, the trajectories of such a system will remain positive if , . From Lemma 6 in [14], it is easy to verify that the first subsystem is unstable. Taking , , , and solving the matrix inequalities (43) and (45) in Theorem 3 gives rise to

Then, by Step 3 in Algorithm 1, the state feedback gain matrices can be obtained as follows:

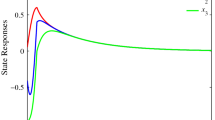
By substituting them into (44) and (46), it is not hard to find that inequalities (44) and (46) are satisfied and , , are Metzler matrices. Then, according to (26) and (27), we can get , and . To illustrate the effectiveness of the proposed results, let us now generate the switching sequences by the average dwell time . We can obtain the state responses shown in Figures 1 and 2 with the initial condition , , , and the switching signal shown in Figure 3. From Figures 1-3, we can see that the state of the closed-loop system is convergent.
5 Conclusions
In this paper, the reliable control problem for positive switched systems with time-varying delays has been discussed. The system studied in this paper consists of stable and unstable subsystems with actuators failures. Using the average dwell time approach, we have proposed a reliable feedback controller and a class of switching signals under which the positive switched system is exponentially stable and has -gain performance for all admissible actuator failures. All the results are formulated in the set of LMIs which can be easily verified or implemented. Our future work will focus on the reliable control problem for discrete-time positive switched systems with time-varying delays.
References
Wong W, Brockett RW: Systems with finite communication bandwidth constraints. I. State estimation problems. IEEE Trans. Autom. Control 1997, 42(9):1294–1299. 10.1109/9.623096
Tomlin C, Pappas GJ, Sastry S: Conflict resolution for air traffic management: a study in multiagent hybrid systems. IEEE Trans. Autom. Control 1998, 43(4):509–521. 10.1109/9.664154
Varaiya P: Smart cars on smart roads: problems of control. IEEE Trans. Autom. Control 1993, 38(2):195–207. 10.1109/9.250509
Shorten R, Wirth F, Leith D: A positive systems model of TCP-like congestion control: asymptotic results. IEEE/ACM Trans. Netw. 2006, 14(3):616–629.
Shorten R, Leith D, Foy J, Kilduff R: Towards an analysis and design framework for congestion control in communication networks. Proceedings of the 12th Yale Workshop on Adaptive and Learning Systems 2003.
Hernandez-Varga E, Middleton R, Colaneri P, Blanchini F: Discrete-time control for switched positive systems with application to mitigating viral escape. Int. J. Robust Nonlinear Control 2011, 21(10):1093–1111. 10.1002/rnc.1628
Jadbabaie A, Lin J, Morse A: Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48(6):988–1001. 10.1109/TAC.2003.812781
Kaczorek T: The choice of the forms of Lyapunov functions for a positive 2D Roesser model. Int. J. Appl. Math. Comput. Sci. 2007, 17(4):471–475.
Kaczorek T: A realization problem for positive continuous-time systems with reduced numbers of delays. Int. J. Appl. Math. Comput. Sci. 2007, 16(3):325–331.
Benvenuti L, Santis A, Farina L (Eds): Lecture Notes in Control and Information Sciences In Positive Systems. Springer, Berlin; 2003.
Rami M, Tadeo F, Benzaouia A: Control of constrained positive discrete systems. Proceedings of American Control Conference 2007, 5851–5856.
Rami M, Tadeo F: Positive observation problem for linear discrete positive systems. Proceedings of the 45th IEEE Conference on Decision and Control 2006, 4729–4733.
Zhao X, Zhang L, Shi P: Stability of a class of switched positive linear time-delay systems. Int. J. Robust Nonlinear Control 2012. doi:10.1002/rnc.2777
Liu X, Dang C: Stability analysis of positive switched linear systems with delays. IEEE Trans. Autom. Control 2011, 56(7):1684–1690.
Fornasini E, Valcher M: Stability and stabilizability of special classes of discrete-time positive switched systems. Proceedings of American Control Conference 2011, 2619–2624.
Zhao X, Zhang L, Shi P, Liu M: Stability of switched positive linear systems with average dwell time switching. Automatica 2012, 48(6):1132–1137. 10.1016/j.automatica.2012.03.008
Xiang W, Xiao J: Stability analysis and control synthesis of switched impulsive systems. Int. J. Robust Nonlinear Control 2012, 22(13):1440–1459. 10.1002/rnc.1757
Xiang W, Xiao J, Iqbal MN:Asymptotic stability, gain, boundness analysis, and control synthesis for switched systems: a switching frequency approach. Int. J. Adapt. Control Signal Process. 2012, 26(4):350–373. 10.1002/acs.1287
Ucar A: A prototype model for chaos studies. Int. J. Eng. Sci. 2002, 40(2):251–258.
Ucar A: On the chaotic behavior of a prototype delayed dynamical system. Chaos Solitons Fractals 2003, 16(2):187–194. 10.1016/S0960-0779(02)00160-1
Karimi HR, Gao H:New delay-dependent exponential synchronization for uncertain neural networks with mixed time delays. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 2010, 40(1):173–185.
Mahmoud MS, Shi P:Robust stability, stabilization and control of time-delay systems with Markovian jump parameters. Int. J. Robust Nonlinear Control 2003, 13(8):755–784. 10.1002/rnc.744
Xiang Z, Wang R: Non-fragile observer design for nonlinear switched systems with time delay. Int. J. Intell. Comput. Cybern. 2009, 2(1):175–189. 10.1108/17563780910939291
Xiang ZR, Wang RH: Robust control for uncertain switched non-linear systems with time delay under asynchronous switching. IET Control Theory Appl. 2009, 3(8):1041–1050. 10.1049/iet-cta.2008.0150
Xiang Z, Wang R: Robust reliable control for uncertain switched nonlinear systems with time delay. Proceedings of the 7th World Congress on Intelligent Control and Automation 2008, 5487–5491.
Song Y, Xiang Z, Chen Q, Hu W: Robust reliable control of switched uncertain systems with time-varying delay. Int. J. Syst. Sci. 2006, 37(15):1077–1087. 10.1080/00207720600879658
Xiang Z, Sun YN, Chen Q: Robust reliable stabilization of uncertain switched neutral systems with delayed switching. Appl. Math. Comput. 2011, 217(23):9835–9844. 10.1016/j.amc.2011.04.082
Xiang Z, Wang R, Chen Q: Robust reliable stabilization of stochastic switched nonlinear systems under asynchronous switching. Appl. Math. Comput. 2011, 217(19):7725–7736. 10.1016/j.amc.2011.02.076
Li L, Feng J, Dimirovski GM, Zhao J:Reliable stabilization and robust control for switched systems with faulty actuators: an average dwell time approach. Proceedings of American Control Conference 2009, 1072–1077.
Mason O, Shorten R: On linear copositive Lyapunov functions and the stability of switched positive linear systems. IEEE Trans. Autom. Control 2007, 52(7):1346–1349.
Sun X, Wang W, Liu G, Zhao J: Stability analysis for linear switched systems with time-varying delay. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 2008, 38(2):528–533.
Hespanha JP, Morse AS: Stability of switched systems with average dwell time. 3. Proceedings of the 38rd IEEE Conference on Decision and Control 1999, 2655–2660.
Xiang M, Xiang Z:Stability, -gain and control synthesis for positive switched systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2013, 9(1):9–17.
Acknowledgements
This research was supported by the National Natural Science Foundation of China under Grant Nos. 60974027 and 61273120.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
MX carried out the main results of this article and drafted the manuscript. ZX directed the study and helped inspection. All the authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xiang, M., Xiang, Z. Reliable control of positive switched systems with time-varying delays. Adv Differ Equ 2013, 25 (2013). https://doi.org/10.1186/1687-1847-2013-25
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-25