Existence results for fractional neutral functional integro-differential evolution equations with infinite delay in Banach spaces

Abstract

In this paper, we investigate the existence results for a class of abstract fractional neutral integro-differential evolution systems involving the Caputo derivative in Banach spaces. The main techniques rely on the fractional calculus, properties of characteristic solution operators, Mönch’s fixed point theorem via measures of noncompactness. Particularly, we do not assume that characteristic solution operators are compact. The application is given to illustrate the theory. The results of this article are generalization and improvement of the recent results on this issue.

MSC:26A33, 34A12, 47H08, 47H10.

1 Introduction

Fractional derivatives provide an excellent tool for the description of memory and hereditary properties of various materials and processes. For more details on fractional calculus theory and applications, one can see the monographs of Kilbas et al. [1], Lakshmikantham et al. [2], Miller and Ross [3], Podlubny [4], Baleanu et al. [5–7] and the papers [8–12] as well as the references therein.

Recently, the existence of solutions for fractional semilinear differential or integro-differential equations is one of the theoretical fields investigated by many authors [11, 13–16]. Very recently, Ji et al. [17] studied the controllability of impulsive differential systems with nonlocal conditions by using Mönch’s fixed point theorem and Wang et al. [18] established the sufficient conditions for nonlocal controllability for fractional evolution systems and the results were obtained by using fractional calculus and Mönch’s fixed point theorem.

However, to the best of our knowledge, no work has been reported on the existence results for fractional neutral integro-differential systems with infinite delay in an abstract phase space via measures of noncompactness combined with the help of characteristic solution operators.

Our aim of this paper is to close the gap, and motivated by works [11, 17, 18], in this paper we investigate the existence of solutions of fractional neutral integro-differential systems with infinite delay of the form

$${}^{C}D^q[x(t)-g(t,x_t)]=Ax(t)+f(t,x_t,{\int }_0^{t}h(t,s,x_s)ds),t\in J:=[0,b],$$

(1.1)

$$x_0=\varphi \in {\mathcal{B}}_h,t\in (-\mathrm{\infty },0],$$

(1.2)

where ${}^{C}D^q$ is the Caputo fractional derivative of order $0<q<1$, A is the infinitesimal generator of a strongly continuous semigroup $\{T(t),t\ge 0\}$ in a Banach space X, which means that there exists $M_1\ge 1$ such that ${sup}_{t\in J}\parallel T(t)\parallel \le M_1$, $f:J\times {\mathcal{B}}_h\times X$, $g:J\times {\mathcal{B}}_h$ and $h:J\times J\times {\mathcal{B}}_h$ are given functions, where ${\mathcal{B}}_h$ is a phase space defined in Section 2. The histories $x_t:(-\mathrm{\infty },0]\to X$, defined by $x_t(s)=x(t+s)$, $s\le 0$, belong to some abstract phase space ${\mathcal{B}}_h$.

The paper is organized as follows. In Section 2, we recall some basic definitions, notations and preliminary facts. Section 3 is devoted to the existence results for fractional neutral integro-differential evolution systems with infinite delay. The application of our theoretical results is given in Section 4. The last section is devoted to our conclusions.

2 Preliminaries

In this section, we mention notations, definitions, lemmas and preliminary facts needed to establish our main results.

Throughout this paper, we denote by X a Banach space with the norm $\parallel \cdot \parallel$. Let Y be another Banach space, let $L_b(X,Y)$ denote the space of bounded linear operators from X to Y. We also use ${\parallel f\parallel }_{L^p(J,R^{+})}$ norm of f whenever $f\in L^p(J,R^{+})$ for some p with $1\le p\le \mathrm{\infty }$. Let $L^p(J,X)$ denote the Banach space of functions $f:J\times {\mathcal{B}}_h\times X\to X$ which are Bochner integrable normed by ${\parallel f\parallel }_{L^p(J,X)}$. Let $\mathcal{C}(J,X)$, be the Banach space of continuous functions from J into X with the usual supremum norm ${\parallel x\parallel }_{\mathcal{C}}:={sup}_{t\in J}\parallel x(t)\parallel$, for $x\in \mathcal{C}$.

In this paper, we assume that $A:D(A)\subset X\to X$ is the infinitesimal generator of a strongly continuous semigroup $T(\cdot )$, then there exists a constant $M\le 1$. Without loss of generality, we assume that $0\in \rho (A)$. Then it is possible to define the fractional power $A^{\alpha }$ for $0<\alpha \le 1$, as a closed linear operator on its domain $D(A^{\alpha })$ with inverse $A^{-\alpha }$ (see [19]). The following are basic properties of $A^{\alpha }$.

• (i) $D(A^{\alpha })$ is a Banach space with the norm ${\parallel x\parallel }_{\alpha }=\parallel A^{\alpha }x\parallel$ for $x\in D(A^{\alpha })$.

• (ii) $T(t):X\to X_{\alpha }$ for $t\ge 0$.

• (iii) $A^{\alpha }T(t)x=T(t)A^{\alpha }x$ for each $x\in D(A^{\alpha })$ and $t\ge 0$.

• (iv) For every $t>0$, $A^{\alpha }T(t)$ is bounded on X and there exists $M_{\alpha }>0$ such that

  $$\parallel A^{\alpha }T(t)\parallel \le \frac{M_{\alpha }}{t^{\alpha }}.$$

• (v) $A^{-\alpha }$ is a bounded linear operator for $0\le \alpha \le 1$ in X.

Now we define the abstract phase space ${\mathcal{B}}_h$, which has been used in [20]. Assume that $h:(-\mathrm{\infty },0]\to (0,+\mathrm{\infty })$ is a continuous function with $l={\int }_{-\mathrm{\infty }}^{0}h(t)dt<+\mathrm{\infty }$. For any $a>0$, we define

$$\mathcal{B}=\{\psi :[-a,0]\to X\text{ such that }\psi (t)\text{ is bounded and measurable}\},$$

and equip the space ℬ with the norm

$${\parallel \psi \parallel }_{[-a,0]}=\underset{s\in [-a,0]}{sup}\parallel \psi (s)\parallel ,\mathrm{\forall }\psi \in \mathcal{B}.$$

Let us define

$$\begin{array}{rcl}{\mathcal{B}}_h& =& \{\psi :(-\mathrm{\infty },0]\to X\text{ such that for any }c>0,\psi {|}_{[-c,0]}\in \mathcal{B}\\ \text{and }{\int }_{-\mathrm{\infty }}^{0}h(s){\parallel \psi \parallel }_{[s,0]}ds<+\mathrm{\infty }\}.\end{array}$$

If ${\mathcal{B}}_h$ is endowed with the norm

$${\parallel \psi \parallel }_{{\mathcal{B}}_h}={\int }_{-\mathrm{\infty }}^{0}h(s){\parallel \psi \parallel }_{[s,0]}ds,\mathrm{\forall }\psi \in {\mathcal{B}}_h,$$

then it is clear that $({\mathcal{B}}_h,{\parallel \cdot \parallel }_{{\mathcal{B}}_h})$ is a Banach space.

Now we consider the space

$${\mathcal{B}}_h^{\mathrm{\prime }}=\{x:(-\mathrm{\infty },b]\to X\text{ such that }x{|}_J\in \mathcal{C}(J,X),x_0=\varphi \in {\mathcal{B}}_h\}.$$

Set ${\parallel \cdot \parallel }_b$ be a seminorm in ${\mathcal{B}}_h^{\mathrm{\prime }}$ defined by

$${\parallel x\parallel }_b={\parallel \varphi \parallel }_{{\mathcal{B}}_h}+sup\{\parallel x(s)\parallel :s\in [0,b]\},x\in {\mathcal{B}}_h^{\mathrm{\prime }}.$$

Lemma 2.1 (See [20])

Assume $x\in {\mathcal{B}}_h^{\mathrm{\prime }}$, then for $t\in J$, $x_t\in {\mathcal{B}}_h$. Moreover,

$$l|x(t)|\le {\parallel x_t\parallel }_{{\mathcal{B}}_h}\le {\parallel \varphi \parallel }_{{\mathcal{B}}_h}+l\underset{s\in [0,t]}{sup}|x(s)|,$$

where $l={\int }_{-\mathrm{\infty }}^{0}h(t)dt<+\mathrm{\infty }$.

Let us recall the following known definitions. For more details see [1, 3, 6].

Definition 2.1 The fractional integral of order α with the lower limit zero for a function f is defined as

$$I^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t\frac{f(s)}{{(t-s)}^{1-\alpha }}ds,t>0,\alpha >0,$$

provided the right-hand side is pointwise defined on $[0,\mathrm{\infty })$, where $\mathrm{\Gamma }(\cdot )$ is the gamma function, which is defined by $\mathrm{\Gamma }(\alpha )={\int }_0^{\mathrm{\infty }}{t}^{\alpha -1}{e}^{-t}dt$.

Definition 2.2 The Riemann-Liouville fractional derivative of order $\alpha >0$, $n-1<\alpha <n$, $n\in N$, is defined as

$${}^{(R-L)}D_{0+}^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\left(\frac{d}{dt}\right)}^n{\int }_0^t{(t-s)}^{n-\alpha -1}f(s)ds,$$

where the function $f(t)$ has absolutely continuous derivative up to order $(n-1)$.

Definition 2.3 The Caputo derivative of order α for a function $f:[0,\mathrm{\infty })\to R$ can be written as

$$D^{\alpha }f(t)=D^{\alpha }(f(t)-\sum _{k=0}^{n-1}\frac{t^k}{k!}{f}^{(k)}(0)),t>0,n-1<\alpha <n.$$

Remark 2.1

• (i) If $f(t)\in C^n[0,\mathrm{\infty })$, then

  $${}^{C}D^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(n-\alpha )}{\int }_0^t\frac{f^{(n)}(s)}{{(t-s)}^{\alpha +1-n}}ds=I^{n-\alpha }{f}^{(n)}(t),t>0,n-1<\alpha <n.$$

• (ii) The Caputo derivative of a constant is equal to zero.

• (iii) If f is an abstract function with values in X, then integrals which appear in Definitions 2.1 and 2.2 are taken in Bochner’s sense.

Definition 2.4 (See [11])

A continuous function $x:(-\mathrm{\infty },b]\to X$ is said to be a mild solution of system (1.1)-(1.2) if $x_0=\varphi \in {\mathcal{B}}_h$ on $(-\mathrm{\infty },0]$ and the following integral equation

$$\begin{array}{rcl}x(t)& =& \mathcal{T}(t)[\varphi (0)-g(0,\varphi (0))]+g(t,x_t)+{\int }_0^t{(t-s)}^{q-1}A\mathcal{S}(t-s)g(s,x_s)ds\\ +{\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)f(s,x_s,{\int }_0^{s}h(s,\tau ,x_{\tau })d\tau )ds,t\in J,\end{array}$$

(2.1)

is satisfied, where $\mathcal{T}(\cdot )$ and $\mathcal{S}(\cdot )$ are called characteristic solution operators and given by

$$\mathcal{T}={\int }_0^{\mathrm{\infty }}{\xi }_q(\theta )T\left(t^q\theta \right)d\theta ,\mathcal{S}=q{\int }_0^{\mathrm{\infty }}\theta {\xi }_q(\theta )T\left(t^q\theta \right)d\theta ,$$

and for $\theta \in (0,\mathrm{\infty })$

$$\begin{array}{c}{\xi }_q(\theta )=\frac{1}{q}{\theta }^{-1-\frac{1}{q}}{\overline{w}}_q\left({\theta }^{-\frac{1}{q}}\right)\ge 0,\hfill \\ {\overline{w}}_q(\theta )=\frac{1}{\pi }\sum _{n=1}^{\mathrm{\infty }}{(-1)}^{n-1}{\theta }^{-nq-1}\frac{\mathrm{\Gamma }(nq+1)}{n!}sin(n\pi q).\hfill \end{array}$$

Here, ${\xi }_q$ is a probability density function defined on $(0,\mathrm{\infty })$, that is

$${\xi }_q(\theta )\ge 0,\theta \in (0,\mathrm{\infty })\text{and}{\int }_0^{\mathrm{\infty }}{\xi }_q(\theta )d\theta =1.$$

The following results of $\mathcal{T}(\cdot )$ and $\mathcal{S}(\cdot )$ are used throughout this paper.

Remark 2.2 (See [11])

It is not difficult to verify that for $\nu \in [0,1]$,

$${\int }_0^{\mathrm{\infty }}{\theta }^{\nu }{\xi }_q(\theta )d\theta ={\int }_0^{\mathrm{\infty }}{\theta }^{-q\nu }{\overline{w}}_q(\theta )d\theta =\frac{\mathrm{\Gamma }(1+\nu )}{\mathrm{\Gamma }(1+q\nu )}.$$

Lemma 2.2 (See [11, 18])

The operators and 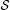have the following properties:

• (i) For any fixed $t\ge 0$, and 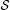are linear and bounded operators, that is, for any $x\in X$,

  $$\parallel \mathcal{T}(t)x\parallel \le M\parallel x\parallel \mathit{\text{and}}\parallel \mathcal{S}(t)x\parallel \le \frac{qM}{\mathrm{\Gamma }(1+q)}\parallel x\parallel .$$

• (ii) $\{\mathcal{T}(t),t\ge 0\}$ and $\{\mathcal{S}(t),t\ge 0\}$ are strongly continuous.

• (iii) For $t\in J$ and any bounded subsets $D\subset X$, $t\to \{\mathcal{T}(t)x:x\in D\}$ and $t\to \{\mathcal{S}(t)x:x\in D\}$ are equicontinuous if $\parallel T(t_2^q(\theta ))x-T(t_1^q(\theta ))x\parallel \to 0$ with respect to $x\in D$ as $t_2\to t_1$ for each fixed $\theta \in [0,\mathrm{\infty }]$.

• (iv) For any $x\in X$, $\alpha ,\beta \in (0,1)$, we have

  $$\begin{array}{c}A{T}_q(t)x=A^{1-\beta }{T}_q(t)A^{\beta }x,t\in J,\hfill \\ \parallel A^{\alpha }{T}_q(t)\parallel \le \frac{q{M}_{\alpha }\mathrm{\Gamma }(2-\alpha )}{\mathrm{\Gamma }(1+q(1-\alpha ))}{t}^{-\alpha q},0<t\le b.\hfill \end{array}$$

Moreover, let us recall some definitions and properties of the measures of noncompactness.

Definition 2.5 (See [17])

Let $E^{+}$ be a positive cone of an ordered Banach space $(E,\le )$. A function Φ defined on the set of all bounded subsets of the Banach space X with values in $E^{+}$ is called a measure of noncompactness (MNC) on X iff $\mathrm{\Phi }(\overline{co}\mathrm{\Omega })=\mathrm{\Phi }(\mathrm{\Omega })$ for all bounded subsets $\mathrm{\Omega }\subseteq X$, where $\overline{co}\mathrm{\Omega }$ stands for the closed convex hull of Ω.

The MNC Φ is said to be

• (1) Monotone iff for all bounded subsets ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ of X we have:

  $$({\mathrm{\Omega }}_1\subseteq {\mathrm{\Omega }}_2)\Rightarrow (\mathrm{\Phi }({\mathrm{\Omega }}_1)\le \mathrm{\Phi }({\mathrm{\Omega }}_2));$$

• (2) Nonsingular iff $\mathrm{\Phi }(\{a\}\cup \mathrm{\Omega })=\mathrm{\Phi }(\mathrm{\Omega })$ for every $a\in X$, $\mathrm{\Omega }\subset X$;

• (3) Regular iff $\mathrm{\Phi }(\mathrm{\Omega })=0$ if and only if Ω is relatively compact in X.

One of the many examples of MNC is the noncompactness measure of Hausdorff β defined on each bounded subset Ω of X by

$$\begin{array}{rcl}\beta (\mathrm{\Omega })& =& inf\{ϵ>0;\mathrm{\Omega }\text{ can be covered by a finite number of balls of radii}\\ \text{smaller than }ϵ\}.\end{array}$$

It is well known that MNC β enjoys the above properties and other properties see [21, 24]. For all bounded subsets Ω, ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ of X,

• (4) $\beta ({\mathrm{\Omega }}_1+{\mathrm{\Omega }}_2)\le \beta ({\mathrm{\Omega }}_1)+\beta ({\mathrm{\Omega }}_2)$, where ${\mathrm{\Omega }}_1+{\mathrm{\Omega }}_2=\{x+y:x\in {\mathrm{\Omega }}_1,y\in {\mathrm{\Omega }}_2\}$;

• (5) $\beta ({\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2)\le max\{\beta ({\mathrm{\Omega }}_1),\beta ({\mathrm{\Omega }}_2)\}$;

• (6) $\beta (\lambda \mathrm{\Omega })\le |\lambda |\beta (\mathrm{\Omega })$ for any $\lambda \in R$;

• (7) If the map $Q:D(Q)\subseteq X\to Z$ is Lipschitz continuous with constant k, then ${\beta }_Z(Q\mathrm{\Omega })\le k\beta (\mathrm{\Omega })$ for any bounded subset $\mathrm{\Omega }\subseteq D(Q)$, where Z is a Banach space.

Lemma 2.3 (See [24])

If $W\subset C([a,b],X)$ is bounded and equicontinuous, then $\beta (W(t))$ is continuous for $t\in [a,b]$ and

$$\beta (W)=sup\{\beta (W(t)),t\in [a,b]\},\mathit{\text{where}}W(t)=\{x(t):x\in W\}\subseteq X.$$

Theorem 2.1 (See [18, 22])

If ${\{u_n\}}_{n=1}^{\mathrm{\infty }}$ is a sequence of Bochner integrable functions from J into X with the estimation $\parallel u_n(t)\parallel \le \mu (t)$ for almost all $t\in J$ and every $n\ge 1$, where $\mu \in L^1(J,R)$, then the function $\psi (t)=\beta (\{u_n(t):n\ge 1\})$ belongs to $L^1(J,R)$ and satisfies $\beta (\{{\int }_0^t\psi (s)ds:n\ge 1\})\le 2{\int }_0^t\psi (s)ds$.

The following fixed-point theorem, a nonlinear alternative of Mönch’s type, plays a key role in our proof of system (1.1)-(1.2).

Lemma 2.4 (See [[23], Theorem 2.2])

Let D be a closed convex subset of a Banach space X and $0\in D$. Assume that $F:D\to X$ is a continuous map which satisfies Mönch’s condition, that is, ($M\subseteq D$ is countable, $M\subseteq \overline{co}(\{0\}\cup F(M))\Rightarrow \overline{M}$ is compact). Then F has a fixed point in D.

3 Existence results

In this section, we present and prove the existence results for problem (1.1)-(1.2). In order to prove the main theorem of this section, we list the following hypotheses.

(H1)

• (i) A generates a strongly continuous semigroup $\{T(t):t\ge 0\}$ in X;

• (ii) For all bounded subsets $D\subset X$ and $x\in D$, $\parallel T(t_2^q\theta )x-T(t_1^q\theta )x\parallel \to 0$ as $t_2\to t_1$ for each fixed $\theta \in (0,\mathrm{\infty })$.

(H2) The function $f:J\times {\mathcal{B}}_h\times X\to X$ satisfies the following:

• (i) $f(\cdot ,\varphi ,x)$ is measurable for all $(\varphi ,x)\in {\mathcal{B}}_h\times X$ and $f(t,\cdot ,\cdot )$ is continuous for a.e. $t\in J$ and for $x\in {\mathcal{B}}_h$, $f(\cdot ,\cdot ,x):[0,T]\to X$ is strongly measurable.

• (ii) There exists a constant $q_1\in (0,q)$ and $m\in L^{\frac{1}{q_1}}(J,R^{+})$ and a nondecreasing continuous function, there is a positive integrable function $\mathrm{\Omega }:R^{+}\to R^{+}$ such that $\parallel f(t,\varphi ,x)\parallel \le m(t)\mathrm{\Omega }({\parallel \varphi \parallel }_{{\mathcal{B}}_h}+\parallel x\parallel )$, for all $(t,\varphi ,x)\in J\times {\mathcal{B}}_h\times X$, where Ω satisfies $lim{inf}_{n\to \mathrm{\infty }}\frac{\mathrm{\Omega }(n)}{n}=0$.

• (iii) There exists a constant $q_2\in (0,q)$ and $h\in L^{\frac{1}{q_2}}(J,R^{+})$ such that, for any bounded subset $D_1\subset X$, $F_1\subset {\mathcal{B}}_h$,

  $$\beta (f(t,F_1,D_1))\le \eta (t)[\underset{-\mathrm{\infty }<\theta \le 0}{sup}\beta (F_1(\theta ))+\beta (D_1)]\text{for a.e. }t\in J,$$

where $F_1(\theta )=\{v(\theta ):v\in D_1\}$ and β is the Hausdorff MNC.

(H3) The function $h:J\times J\times {\mathcal{B}}_h\to X$ satisfies:

• (i) $h(\cdot ,\varphi ,x)$ is measurable for $(\varphi ,x)\in {\mathcal{B}}_h\times X$ and $h(t,\cdot ,\cdot )$ is continuous for a.e. $t\in J$.

• (ii) There exists a constant $H_0>0$ such that $\parallel h(t,s,\varphi )\parallel \le H_0(1+{\parallel \varphi \parallel }_{{\mathcal{B}}_h})$, for all $t,s\in J$, $\varphi \in {\mathcal{B}}_h$.

• (iii) There exists $\zeta \in L^1(J^2,R^{+})$ such that for any bounded subset $D_2\subset X$,

  $$\beta (h(t,s,D_2))\le \zeta (t,s)\left[\underset{-\mathrm{\infty }<\theta \le 0}{sup}\beta (D_2(\theta ))\right]\text{for a.e. }t\in J$$

with ${\zeta }^{\ast }={sup}_{s\in J}{\int }_0^s\zeta (t,\tau )d\tau <\mathrm{\infty }$.

(H4) The function $g:J\times {\mathcal{B}}_h$ is continuous and there exists a constant $H_1>0$, $0<\alpha <1$ such that g is $X_{\alpha }$ valued and

$$\begin{array}{r}\parallel A^{\beta }g(t,x)-A^{\beta }g(t,y)\parallel \le H_1{\parallel x-y\parallel }_{{\mathcal{B}}_h},x,y\in {\mathcal{B}}_h,t\in J:=[0,b],\\ \parallel A^{\beta }g(t,x)\parallel \le H_1(1+{\parallel x\parallel }_{{\mathcal{B}}_h}).\end{array}$$

For our convenience, let us take ${\kappa }_i:={[(\frac{1-q_i}{q-q_i})b^{\frac{q-q_i}{1-q_i}}]}^{1-q_i}$, $i=0,1,2$. $M_4:={\kappa }_1{\parallel m\parallel }_{L^{\frac{1}{q_1}}(J,R^{+})}$, and $M_6={\kappa }_2{\parallel \eta \parallel }_{L^{\frac{1}{q_2}}(J,R^{+})}$.

Theorem 3.1 Assume that the hypotheses (H1)-(H4) are satisfied, then system (1.1)-(1.2) has at least one mild solution provided that,

$$Z^{\ast }=\frac{2M_1{M}_{6}q}{\mathrm{\Gamma }(1+q)}(1+2{\zeta }^{\ast })<1\mathit{\text{for some}}\frac{1}{2}<q<1.$$

(3.1)

Proof In order to prove the existence of mild solutions for system (1.1)-(1.2), transform it into a fixed point problem.

We consider the operator $\mathrm{\Phi }:{\mathcal{B}}_h^{\prime }\to {\mathcal{B}}_h^{\prime }$ defined by

$$\mathrm{\Phi }x(t)=\{\begin{array}{c}\varphi (t),t\in (-\mathrm{\infty },0],\hfill \\ \mathcal{T}(t)[\varphi (0)-g(0,\varphi (0))]+g(t,x_t)+{\int }_0^t{(t-s)}^{q-1}A\mathcal{S}(t-s)g(s,x_s)ds\hfill \\ +{\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)f(s,x_s,{\int }_0^{s}h(s,\tau ,x_{\tau })d\tau )ds,t\in J.\hfill \end{array}$$

(3.2)

For $\varphi \in {\mathcal{B}}_h$, we define $\hat{\varphi }$ by

$$\hat{\varphi }(t)=\{\begin{array}{cc}\varphi (t),\hfill & t\in (-\mathrm{\infty },0],\hfill \\ \mathcal{T}(t)\varphi (0),\hfill & t\in J,\hfill \end{array}$$

then $\hat{\varphi }\in {\mathcal{B}}_h^{\mathrm{\prime }}$. Let $x(t)=y(t)+\hat{\varphi }(t)$, $-\mathrm{\infty }<t\le b$. It is easy to see that x satisfies (2.1) if and only if y satisfies $y_0=0$ and

$$\begin{array}{rcl}y(t)& =& -\mathcal{T}(t)g(0,\varphi )+g(t,y_t+{\hat{\varphi }}_t)+{\int }_0^t{(t-s)}^{q-1}A\mathcal{S}(t-s)g(s,y_s+{\hat{\varphi }}_s)ds\\ +{\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)f(s,y_s+{\hat{\varphi }}_s,{\int }_0^{s}h(s,\tau ,y_{\tau }+{\hat{\varphi }}_{\tau })d\tau )ds.\end{array}$$

Let ${\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }}=\{y\in {\mathcal{B}}_h^{\mathrm{\prime }}:y_0=0\in {\mathcal{B}}_h\}$. For any $y\in {\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }}$,

$$\begin{array}{rcl}{\parallel y\parallel }_b& =& {\parallel y_0\parallel }_{{\mathcal{B}}_h}+sup\{\parallel y(s)\parallel :0\le s\le b\}\\ =& sup\{\parallel y(s)\parallel :0\le s\le b\},\end{array}$$

thus $({\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }},{\parallel \cdot \parallel }_b)$ is a Banach space. Set $B_r=\{y\in {\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }}:{\parallel y\parallel }_b\le r\}$ for some $r>0$, then $B_r\subseteq {\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }}$ is uniformly bounded, and for $y\in B_r$, from Lemma 2.1, we have

$$\begin{array}{rcl}{\parallel y_t+{\hat{\varphi }}_t\parallel }_{{\mathcal{B}}_h}& \le & {\parallel y_t\parallel }_{{\mathcal{B}}_h}+{\parallel {\hat{\varphi }}_t\parallel }_{{\mathcal{B}}_h}\\ \le & l(r+M_1|\varphi (0)|)+{\parallel \varphi \parallel }_{{\mathcal{B}}_h}=r^{\mathrm{\prime }}.\end{array}$$

(3.3)

Define the operator $\tilde{\mathrm{\Phi }}:{\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }}\to {\mathcal{B}}_h^{\mathrm{\prime }\mathrm{\prime }}$ by

$$\tilde{\mathrm{\Phi }}y(t)=\{\begin{array}{c}0,t\in (-\mathrm{\infty },0],\hfill \\ -\mathcal{T}(t)g(0,\varphi )+g(t,y_t+{\hat{\varphi }}_t)+{\int }_0^t{(t-s)}^{q-1}A\mathcal{S}(t-s)g(s,y_s+{\hat{\varphi }}_s)ds\hfill \\ +{\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)f(s,y_s+{\hat{\varphi }}_s,{\int }_0^{s}h(s,\tau ,y_{\tau }+{\hat{\varphi }}_{\tau })d\tau )ds,t\in J.\hfill \end{array}$$

(3.4)

Obviously, the operator Φ has a fixed point is equivalent to $\tilde{\mathrm{\Phi }}$ has one. So, our aim is to show that $\tilde{\mathrm{\Phi }}$ has a fixed point. The proof will be given in several steps.

Step 1: We show that there exists some $r>0$ such that $\tilde{\mathrm{\Phi }}(B_r)\subseteq B_r$. If it is not true, then for each positive number r, there exists a function $y^r(\cdot )\in B_r$ and some $t\in J$ such that $\parallel (\tilde{\mathrm{\Phi }}{y}^r)(t)\parallel >r$.

On the other hand, from hypotheses the (H2)(i), (ii), (H4), Lemma 2.2(i) and Hölder’s inequality, we obtain

$$\begin{array}{rcl}r& <& \parallel \left(\tilde{\mathrm{\Phi }}{y}^r\right)(t)\parallel \\ \le & \parallel -\mathcal{T}(t)g(0,\varphi )\parallel +\parallel g(t,y_t+{\hat{\varphi }}_t)\parallel +\parallel {\int }_0^t{(t-s)}^{q-1}A\mathcal{S}(t-s)g(s,y_s+{\hat{\varphi }}_s)ds\parallel \\ +\parallel {\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)f(s,y_s+{\hat{\varphi }}_s,{\int }_0^{s}h(s,\tau ,y_{\tau }+{\hat{\varphi }}_{\tau })d\tau )ds\parallel \\ :=& I_1+I_2+I_3+I_4.\end{array}$$

Let us estimate, $I_i$, $i=1,2,3,4$. By assumption (H4), we have

$$\begin{array}{l}{I}_1\le M_1\parallel A^{-\beta }\parallel \parallel A^{\beta }g(0,\varphi )\parallel \\ \phantom{I_1}\le M_1{H}_1\parallel A^{-\beta }\parallel (1+{\parallel \varphi \parallel }_{{\mathcal{B}}_h}),\end{array}$$

(3.5)

$$\begin{array}{l}{I}_2\le \parallel A^{-\beta }\parallel \parallel A^{\beta }g(t,y_t+{\hat{\varphi }}_t)\parallel \\ \phantom{I_2}\le H_1\parallel A^{-\beta }\parallel (1+{\parallel y_t+{\hat{\varphi }}_t\parallel }_{{\mathcal{B}}_h})\\ \phantom{I_2}\le H_1\parallel A^{-\beta }\parallel (1+r^{\prime }).\end{array}$$

(3.6)

By using Lemma 2.2 and Hölder’s inequality, one can deduce that

$$\begin{array}{rcl}{I}_3& \le & {\int }_0^t\parallel {(t-s)}^{q-1}{A}^{1-\beta }\mathcal{S}(t-s)A^{\beta }g(s,y_s+{\hat{\varphi }}_s)\parallel ds\\ \le & \frac{M_{1-\beta }\alpha \mathrm{\Gamma }(1+\beta )}{\mathrm{\Gamma }(1+\alpha \beta )}{\int }_0^t{(t-s)}^{\alpha \beta -1}\parallel A^{\beta }g(s,y_s+{\hat{\varphi }}_s)\parallel ds\\ \le & K_1(\alpha ,\beta ){\int }_0^t{(t-s)}^{\alpha \beta -1}{H}_1(1+{\parallel x\parallel }_{{\mathcal{B}}_h})ds\\ \le & K_1(\alpha ,\beta )H_1\frac{T^{\alpha \beta }}{\alpha \beta }(1+r^{\prime }).\end{array}$$

(3.7)

Using assumptions (H2) and (H3), we have

$$\begin{array}{rcl}{I}_4& \le & \parallel {\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)f(s,y_s+{\hat{\varphi }}_s,{\int }_0^{s}h(s,\tau ,y_{\tau }+{\hat{\varphi }}_{\tau }))d\tau \parallel ds\\ \le & \frac{M_1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-s)}^{q-1}m(s)\mathrm{\Omega }({\parallel \varphi \parallel }_{{\mathcal{B}}_h}+\parallel x\parallel )ds\\ \le & \frac{M_1{T}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}m(s)\mathrm{\Omega }(r^{\prime }+b{H}_0(1+r^{\prime }))ds\\ \le & \frac{M_1{T}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}\mathrm{\Omega }(r^{\prime }+b{H}_0(1+r^{\prime }))\underset{t\in J}{sup}m(s).\end{array}$$

(3.8)

Combining estimates (3.5)-(3.8) yields

$$\begin{array}{rcl}{I}_1+I_2+I_3+I_4& <& H_1\parallel A^{-\beta }\parallel [M_1(1+{\parallel \varphi \parallel }_{{\mathcal{B}}_h})+(1+r^{\prime })]+K(\alpha ,\beta )H_1\frac{T^{\alpha \beta }}{\alpha \beta }(1+r^{\prime })\\ +\frac{M_1{T}^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}\mathrm{\Omega }(r^{\prime }+b{H}_0(1+r^{\prime }))\underset{t\in J}{sup}m(s).\end{array}$$

(3.9)

Dividing both sides of (3.9) by r, and taking $r\to \mathrm{\infty }$, we have ≥1, which is a contradiction.

Hence for some positive number r, $\tilde{\mathrm{\Phi }}(B_r)\subseteq B_r$.

Step 2: $\tilde{\mathrm{\Phi }}$ is continuous on $B_r$.

Let ${\{y^n\}}_{n\in N}\subset B_r$ with $y^{(n)}\to y$ in $B_r$ as $n\to \mathrm{\infty }$.

Denote

$$\begin{array}{c}{F}_n(s)=f(s,y_s^{(n)}+{\hat{\varphi }}_s,{\int }_0^{s}h(s,\tau ,y_{\tau }^{(n)}+{\hat{\varphi }}_{\tau })d\tau )\text{and}\hfill \\ F(s)=f(s,y_s+{\hat{\varphi }}_s,{\int }_0^{s}h(s,\tau ,y_{\tau }+{\hat{\varphi }}_{\tau })d\tau ).\hfill \end{array}$$

Then, by using hypotheses (${\mathrm{H}}_2$)(i), (ii), (${\mathrm{H}}_3$)(i), (ii) and Lebesgue’s dominated convergence theorem, we obtain

$${\int }_0^t{(t-s)}^{q-1}\parallel F_n(s)-F(s)\parallel ds\to 0\text{as }n\to \mathrm{\infty },t\in J.$$

(3.10)

Now,

$${\parallel \tilde{\mathrm{\Phi }}{y}^n-\tilde{\mathrm{\Phi }}y\parallel }_{\mathcal{C}}\le \frac{M_{1}q}{\mathrm{\Gamma }(1+q)}{\int }_0^t{(t-s)}^{q-1}\parallel F_n(s)-F(s)\parallel ds.$$

(3.11)

Observing (3.6) and (3.7), we have

$${\parallel \tilde{\mathrm{\Phi }}{y}^n-\tilde{\mathrm{\Phi }}y\parallel }_{\mathcal{C}}\to 0\text{as }n\to \mathrm{\infty },$$

which implies that $\tilde{\mathrm{\Phi }}$ is continuous on $B_r$.

Step 3: $\tilde{\mathrm{\Phi }}(B_r)$ is equicontinuous on J. Indeed, let $z\in \tilde{\mathrm{\Phi }}(B_r)$ and $0\le t_1<t_2\le b$. Then there is $y\in B_r$ such that

$$\begin{array}{c}\parallel z(t_2)-z(t_1)\parallel \hfill \\ \le \parallel \mathcal{T}(t)(t_2)-\mathcal{T}(t)(t_1)\parallel +[\parallel \varphi (0)\parallel +\parallel g(0,\varphi (0)\parallel ]\hfill \\ +\parallel {\int }_0^{t_2}{(t_2-s)}^{q-1}\mathcal{S}(t_2-s)F(s)ds-{\int }_0^{t_1}{(t_1-s)}^{q-1}\mathcal{S}(t_1-s)F(s)ds\parallel \hfill \\ \le \parallel \mathcal{T}(t)(t_2)-\mathcal{T}(t)(t_1)\parallel +[\varphi +\parallel g(0,\varphi (0)\parallel ]+\parallel {\int }_{t_1}^{t_2}{(t_2-s)}^{q-1}\mathcal{S}(t_2-s)F(s)ds\parallel \hfill \\ +\parallel {\int }_{t_1-ϵ}^{t_1}{(t_2-s)}^{q-1}[\mathcal{S}(t_2-s)-\mathcal{S}(t_1-s)]F(s)ds\parallel \hfill \\ +\parallel {\int }_{t_1-ϵ}^{t_1}[{(t_2-s)}^{q-1}-{(t_1-s)}^{q-1}]\mathcal{S}(t_1-s)F(s)ds\parallel \hfill \\ +\parallel {\int }_0^{t_1-ϵ}{(t_2-s)}^{q-1}[\mathcal{S}(t_2-s)-\mathcal{S}(t_1-s)]F(s)ds\parallel \hfill \\ +\parallel {\int }_0^{t_1-ϵ}[{(t_2-s)}^{q-1}-{(t_1-s)}^{q-1}]\mathcal{S}(t_1-s)F(s)ds\parallel .\hfill \end{array}$$

Using Lemma 2.2, we can verify that the right-hand side of the above inequality tends to zero as $t_2\to t_1$. Therefore, $\tilde{\mathrm{\Phi }}(B_r)$ is equicontinuous on J.

Step 4: Mönch’s condition holds.

Suppose that $W\subseteq B_r$ is countable and $W\subseteq conv(\{0\}\cup \tilde{\mathrm{\Phi }}(W))$. We show that $\beta (W)=0$, where β is the Hausdorff MNC. Without loss of generality, we may suppose that $W={\{y^n\}}_{n=1}^{\mathrm{\infty }}$. Now we need to show that $\tilde{\mathrm{\Phi }}(W)(t)$ is relatively compact in X for each $t\in J$.

By Theorem 2.1, we have

$$\begin{array}{c}\beta \left({\{{\tilde{\mathrm{\Phi }}}_{y^n}(s)\}}_{n=1}^{\mathrm{\infty }}\right)\hfill \\ \le \beta \left({\{{\int }_0^t{(t-s)}^{q-1}\mathcal{S}(t-s)F_n(s)ds\}}_{n=1}^{\mathrm{\infty }}\right)\hfill \\ \le \frac{2M_{1}q}{\mathrm{\Gamma }(1+q)}{\int }_0^t{(t-s)}^{q-1}\beta \left({\{F_n(s)ds\}}_{n=1}^{\mathrm{\infty }}\right)ds\hfill \\ \le \frac{2M_{1}q}{\mathrm{\Gamma }(1+q)}{\int }_0^t{(t-s)}^{q-1}\eta (s)[\underset{-\mathrm{\infty }<\theta \le 0}{sup}\beta \left({\{y^n(s+\theta )+\hat{\varphi }(s+\theta )\}}_{n=1}^{\mathrm{\infty }}\right)\hfill \\ +\beta \left({\left\{{\int }_0^{s}h(s,\tau ,y_{\tau }^n+{\hat{\varphi }}_{\tau })d\tau \right\}}_{n=1}^{\mathrm{\infty }}\right)]ds\hfill \\ \le \left[\frac{2M_{1}q}{\mathrm{\Gamma }(1+q)}(1+2{\zeta }^{\ast })M_6\right]\underset{0\le \tau \le s}{sup}\beta (W(\tau ))ds.\hfill \end{array}$$

That is,

$$\beta (\tilde{\mathrm{\Phi }}W(t))\le \frac{2M_1{M}_{6}q}{\mathrm{\Gamma }(1+q)}(1+2{\zeta }^{\ast })\underset{0\le \tau \le s}{sup}\beta (W(\tau ))$$

which implies, by Lemma 2.3, $\beta (\tilde{\mathrm{\Phi }}(W))\le Z^{\ast }\beta (W)$, where $Z^{\ast }$ is defined in condition (3.1). Thus, from Mönch’s condition, we get

$$\beta (W)\le \beta (conv(\{0\}\cup \tilde{\mathrm{\Phi }}(W)))=\beta (\tilde{\mathrm{\Phi }}(W))\le Z^{\ast }\beta (W),$$

which implies that $\beta (W)=0$.

Hence, using Lemma 2.4, $\tilde{\mathrm{\Phi }}$ has a fixed point y in $B_r$. Then $x=y+\hat{\varphi }$ is a mild solution of system (1.1)-(1.2). This completes the proof. □

4 An application

For $1/2<\alpha <1$, consider the following fractional order neutral functional integro-differential of the form

$$\begin{array}{l}{}^{C}D_t^q[z(t,\eta )+{\int }_0^{\pi }b(\theta ,\eta )z(t,\theta )d\theta ]\\ =\frac{{\partial }^2}{\partial {\eta }^2}z(t,\eta )\\ +\mu (t,{\int }_{-\mathrm{\infty }}^t{\mu }_1(s-t)z(s,\eta )ds,{\int }_0^t{\int }_{-\mathrm{\infty }}^0{\mu }_2(s,\eta ,\tau -s)z(\tau ,\eta )d\tau ds),\end{array}$$

(4.1)

$$z(t,0)=z(t,\pi )=0,t\ge 0,$$

(4.2)

$$z(0,\eta )=\psi (\eta ),0\le \eta \le \pi ,$$

(4.3)

where $\mu :J\times [0,1]\times [0,1]\times R\to R$ is continuous functions. To write system (1.1)-(1.3) to the form (4.1)-(4.3), let $X=L^2[0,\pi ]$ and $A:D(A)\subset X\to X$ be defined as follows: $Af=f^{\prime }$ with domain

$$D(A)=\{f\in X:f,f^{\prime }\text{ are absolutely continuous},f^{″}\in X,f(0)=f(\pi )=0\}.$$

It is well known that A is an infinitesimal generator of a semigroup $\{T(t),t\ge 0\}$ in X and is given by $T(t)w(s)=w(t+s)$, for $w\in X$, $T(t)$ is not a compact semigroup on X with $\beta (T(t)D)\le \beta (D)$, where β is the Hausdorff MNC and there exists an $M_1\ge 1$ such that ${sup}_{t\in J}\parallel T(t)\parallel \le M_1$. Moreover, $t\to w(t^{\alpha }\theta +s)x$ is equicontinuous [18] for $t\ge 0$ and $\theta \in (0,\mathrm{\infty })$. Define $f,g:[0,\pi ]\times X\to X$ by

$$\begin{array}{c}g(z)(\eta )={\int }_0^{\pi }b(\theta ,\eta )z(\theta )d\theta ,\hfill \\ f(t,\pi ,{\int }_0^{t}g(s,\pi )ds)(\eta )\hfill \\ =\mu (t,{\int }_{-\mathrm{\infty }}^t{\mu }_1(s-t)z(s,\eta )ds,{\int }_0^t{\int }_{-\mathrm{\infty }}^0{\mu }_2(s,\eta ,\tau -s)z(\tau ,\eta )d\tau ds).\hfill \end{array}$$

We take $\mu (t,{\int }_{-\mathrm{\infty }}^t{\mu }_1(s-t)z(s,\eta )ds,{\int }_0^t{\int }_{-\mathrm{\infty }}^0{\mu }_2(s,\eta ,\tau -s)z(\tau ,\eta )d\tau ds)=C_{0}sin(x(s))$, $C_0$ is a constant. F is Lipschitz continuous for the second variable. Then f satisfies hypotheses (H3) and (H4). This completes the example.

Conclusions

In the current paper, we are focused on establishing the existence result for a class of abstract fractional neutral functional integro-differential evolution systems involving the Caputo fractional derivative in Banach spaces. By using fractional calculus, the properties of characteristic solution operators, Mönch’s fixed point theorem via MNC, we have found the existence results. Here, we do not assume that characteristic solution operators are compact. An example is provided to show the effectiveness of the proposed results.