Adaptive almost surely asymptotically synchronization for stochastic delayed neural networks with Markovian switching

Abstract

In this paper, the problem of the adaptive almost surely asymptotically synchronization for stochastic delayed neural networks with Markovian switching is considered. By utilizing a new nonnegative function and the M-matrix approach, we derive a sufficient condition to ensure adaptive almost surely asymptotically synchronization for stochastic delayed neural networks. Some appropriate parameters analysis and update laws are found via the adaptive feedback control techniques. We also present an illustrative numerical example to demonstrate the effectiveness of the M-matrix-based synchronization condition derived in this paper.

1 Introduction

As we know, the stochastic delayed neural networks (SDNNs) with Markovian switching have played an important role in the fields of science and engineering for their many practical applications, including image processing, pattern recognition, associative memory, and optimization problems [1, 2]. In the past several decades, the characteristics of the SDNNs with Markovian switching, such as the various stability [3, 4], have received a lot of attention from scholars in various fields of nonlinear science. Wang et al. in [5] considered exponential stability for delayed recurrent neural networks with Markovian jumping parameters. Zhang et al. investigated stochastic stability for Markovian jumping genetic regulatory networks with mixed time delays [6]. Huang et al. investigated robust stability for stochastic delayed additive neural networks with Markovian switching [7]. The researchers presented a number of sufficient conditions to achieve the global asymptotic stability and exponential stability for the SDNNs with Markovian switching [8–11]. As is well known, time delays, as a source of instability and oscillations, always appear in various aspects of neural networks. Recently, the time delays of neural networks have received a lot of attention [12–15]. The linear matrix inequality (LMI, for short) approach is one of the most extensively used in recent publications [16, 17].

In recent years, it has been found that the synchronization of the coupled neural networks has potential applications in many fields such as biology and engineering [18–21]. In the coupled nonlinear dynamical systems, many neural networks may experience abrupt changes in their structure and parameters caused by some phenomena such as component failures or repairs, changing subsystem interconnections, and abrupt environmental disturbances. The synchronization may help to protect interconnected neurons from the influence of random perturbations which affect all neurons in the system. Therefore, from the neurophysiological as well as theoretical point of view, it is important to investigate the impact of synchronization on the SDNNs. Moreover, in the adaptive synchronization for the neural networks, the control law needs to be adapted or updated in realtime. So, the adaptive synchronization for neural networks has been used in real neural networks control such as parameter estimation adaptive control, model reference adaptive control, etc. Some stochastic synchronization results have been investigated. For example, in [22], an adaptive feedback controller is designed to achieve complete synchronization for unidirectionally coupled delayed neural networks with stochastic perturbation. In [23], via adaptive feedback control techniques with suitable parameters update laws, several sufficient conditions are derived to ensure lag synchronization for unknown delayed neural networks with or without noise perturbation. In [24], a class of chaotic neural networks is discussed, and based on the Lyapunov stability method and the Halanay inequality lemma, a delay independent sufficient exponential synchronization condition is derived. The simple adaptive feedback scheme has been used for the synchronization for neural networks with or without time-varying delay in [25]. A general model of an array of N linearly coupled delayed neural networks with Markovian jumping hybrid coupling is introduced in [26] and some sufficient criteria have been derived to ensure the synchronization in an array of jump neural networks with mixed delays and hybrid coupling in mean square.

It should be pointed out that, to the best of our knowledge, the adaptive almost surely asymptotically synchronization for the SDNNs with Markovian switching is seldom mentioned although it is of practical importance. Motivated by the above statements, in this paper, we aim to analyze the adaptive almost surely asymptotically synchronization for the SDNNs with Markovian switching. M-matrix-based criteria for determining whether adaptive almost surely asymptotically synchronization for the SDNNs with Markovian switching are developed. An adaptive feedback controller is proposed for the SDNNs with Markovian switching. A numerical simulation is given to show the validity of the developed results.

The rest of this paper is organized as follows: in Section 2, the problem is formulated and some preliminaries are given; in Section 3, a sufficient condition to ensure the adaptive almost surely asymptotically synchronization for the SDNNs with Markovian switching is derived; in Section 4, an example of numerical simulation is given to illustrate the validity of the results; Section 5 gives the conclusion of the paper.

2 Problem formulation and preliminaries

Throughout this paper, ℰ stands for the mathematical expectation operator, ${\parallel x\parallel }^2$ is used to denote a vector norm defined by ${\parallel x\parallel }^2={\sum }_{i=1}^n{x}_i^2$, ‘T’ represents the transpose of a matrix or a vector, $I_n$ is an n-dimensional identical matrix.

Let ${\{r(t)\}}_{t\ge 0}$ be a right-continuous Markov chain on the probability space taking values in a finite state space $S=\{1,2,\dots ,N\}$ with generator $\Gamma ={({\gamma }_{ij})}_{N\times N}$ given by

$$P\{r(t+\delta )=j|r(t)=i\}=\{\begin{array}{ll}{\gamma }_{ij}\delta +o(\delta )& \text{if }i\ne j,\\ 1+{\gamma }_{ii}\delta +o(\delta )& \text{if }i=j,\end{array}$$

where $\delta >0$ and ${\gamma }_{ij}\ge 0$ is the transition rate from i to j if $i\ne j$ while

$${\gamma }_{ij}=-\sum _{j\ne i}{\gamma }_{ij}.$$

We denote $r(0)=r_0$.

In this paper, we consider the neural network called drive system and represented by the compact form as follows:

$$dx(t)=[-C(r(t))x(t)+A(r(t))f(x(t))+B(r(t))f\left(x(t-\tau (t))\right)+D(r(t))]dt,$$

(1)

where $t\ge 0$ is the time, $x(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T\in R^n$ is the state vector associated with n neurons, $f(x(t))={(f_1(x_1(t)),f_2(x_2(t)),\dots ,f_n(x_n(t)))}^T\in R^n$ denote the activation functions of the neurons, $\tau (t)$ is the transmission delay satisfying that $0<\tau (t)\le \overline{\tau }$ and $\dot{\tau }(t)\le \hat{\tau }<1$, where $\overline{\tau }$, $\hat{\tau }$ are constants. As a matter of convenience, for $t\ge 0$, we denote $r(t)=i$ and $A(r(t))=A^i$, $B(r(t))=B^i$, $C(r(t))=C^i$, $D(r(t))=D^i$, respectively. In model (1), furthermore, $\mathrm{\forall }i\in S$, $C^i=diag\{c_1^i,c_2^i,\dots ,c_n^i\}$ (i.e., $C^i$ is a diagonal matrix) has positive and unknown entries $c_k^i>0$, $A^i={(a_{jk}^i)}_{n\times n}$ and $B^i={(b_{jk}^i)}_{n\times n}$ are the connection weight and the delayed connection weight matrices, respectively. $D^i={(d_1^i,d_2^i,\dots ,d_n^i)}^T\in R^n$ is the constant external input vector.

For the drive system (1), a response system is constructed as follows:

$$\begin{array}{rl}dy(t)=& [-C(r(t))y(t)+A(r(t))f(y(t))\\ +B(r(t))f\left(y(t-\tau (t))\right)+D(r(t))+U(t)]dt\\ +\sigma (t,r(t),y(t)-x(t),y(t-\tau (t))-x(t-\tau (t)))d\omega (t),\end{array}$$

(2)

where $y(t)$ is the state vector of the response system (2), $U(t)={(u_1(t),u_2(t),\dots ,u_n(t))}^T\in R^n$ is a control input vector with the form of

$$\begin{array}{rl}U(t)& =K(t)(y(t)-x(t))\\ =diag\{k_1(t),k_2(t),\dots ,k_n(t)\}(y(t)-x(t)),\end{array}$$

(3)

$\omega (t)={({\omega }_1(t),{\omega }_2(t),\dots ,{\omega }_n(t))}^T$ is an n-dimensional Brown moment defined on a complete probability space $(\mathrm{\Omega },\mathcal{F},P)$ with a natural filtration ${\{{\mathcal{F}}_t\}}_{t\ge 0}$ (i.e., ${\mathcal{F}}_t=\sigma \{\omega (s):0\le s\le t\}$ is a σ-algebra) and is independent of the Markovian process ${\{r(t)\}}_{t\ge 0}$, and $\sigma :R_{+}\times S\times R^n\times R^n\to R^{n\times n}$ is the noise intensity matrix and can be regarded as a result of the occurrence of eternal random fluctuation and other probabilistic causes.

Let $e(t)=y(t)-x(t)$. For the purpose of simplicity, we mark $e(t-\tau (t))=e_{\tau }(t)$ and $f(x(t)+e(t))-f(x(t))=g(e(t))$. From the drive system (1) and the response system (2), the error system can be represented as follows:

$$\begin{array}{rl}de(t)=& [-C(r(t))e(t)+A(r(t))g(e(t))+B(r(t))g(e_{\tau }(t))+U(t)]dt\\ +\sigma (t,r(t),e(t),e_{\tau }(t))d\omega (t).\end{array}$$

(4)

The initial condition associated with system (4) is given in the following form:

$$e(s)=\xi (s),s\in [-\overline{\tau },0]$$

for any $\xi \in L_{{\mathcal{F}}_0}^2([-\overline{\tau },0],R^n)$, where $L_{{\mathcal{F}}_0}^2([-\overline{\tau },0],R^n)$ is the family of all ${\mathcal{F}}_0$-measurable $\mathcal{C}([-\overline{\tau },0];R^n)$-value random variables satisfying that ${sup}_{-\overline{\tau }\le s\le 0}E{|\xi (s)|}^2<\mathrm{\infty }$, and $\mathcal{C}([-\overline{\tau },0];R^n)$ denotes the family of all continuous $R^n$-valued functions $\xi (s)$ on $[-\overline{\tau },0]$ with the norm $\parallel \xi \parallel ={sup}_{-\overline{\tau }\le s\le 0}|\xi (s)|$.

To obtain the main result, we need the following assumptions.

Assumption 1 The activation functions of the neurons $f(x(t))$ satisfy the Lipschitz condition. That is, there exists a constant $L>0$ such that

$$|f(u)-f(v)|\le L|u-v|,\mathrm{\forall }u,v\in R^n.$$

Assumption 2 The noise intensity matrix $\sigma (\cdot ,\cdot ,\cdot ,\cdot )$ satisfies the linear growth condition. That is, there exist two positives $H_1$ and $H_2$ such that

$$trace{\left(\sigma (t,r(t),u(t),v(t))\right)}^T\left(\sigma (t,r(t),u(t),v(t))\right)\le H_1{|u(t)|}^2+H_2{|v(t)|}^2$$

for all $(t,r(t),u(t),v(t))\in R_{+}\times S\times R^n\times R^n$.

Assumption 3 In the drive system (1)

$$f(0)\equiv 0,\sigma (t_0,r_0,0,0)\equiv 0.$$

Remark 1 Under Assumption 1∼Assumption 3, the error system (4) admits an equilibrium point (or trivial solution) $e(t,\xi )$, $t\ge 0$.

The following stability concept and synchronization concept are needed in this paper.

Definition 1 The trivial solution $e(t,\xi )$ of the error system (4) is said to be almost surely asymptotically stable if

$$P(\underset{t\to \mathrm{\infty }}{lim}|x(t;i_0,\xi )|=0)=1$$

for any $\xi \in L_{{\mathcal{L}}_0}^p([-\overline{\tau },0];R^n)$.

The response system (2) and the drive system (1) are said to be almost surely asymptotically synchronized if the error system (4) is almost surely asymptotically stable.

The main purpose of the rest of this paper is to establish a criterion of the adaptive almost surely asymptotically synchronization of system (1) and response system (2) by using the adaptive feedback control and M-matrix techniques.

To this end, we introduce some concepts and lemmas which will be frequently used in the proofs of our main results.

Definition 2 [27]

A square matrix $M={(m_{ij})}_{n\times n}$ is called a nonsingular M-matrix if M can be expressed in the form $M=s{I}_n-G$ with some $G\ge 0$ (i.e., each element of G is nonnegative) and $s>\rho (G)$, where $\rho (G)$ is the spectral radius of G.

Lemma 1 [8]

If $M={(m_{ij})}_{n\times n}\in R^{n\times n}$ with $m_{ij}<0$ ($i\ne j$), then the following statements are equivalent:

• (1) M is a nonsingular M-matrix.

• (2) Every real eigenvalue of M is positive.

• (3) M is positive stable. That is, $M^{-1}$ exists and $M^{-1}>0$ (i.e., $M^{-1}\ge 0$ and at least one element of $M^{-1}$ is positive).

Lemma 2 [5]Let $x\in R^n$, $y\in R^n$. Then

$$x^{T}y+y^{T}x\le ϵx^{T}x+{ϵ}^{-1}{y}^{T}y$$

for any $ϵ>0$.

Consider an n-dimensional stochastic delayed differential equation (SDDE, for short) with Markovian switching

$$dx(t)=f(t,r(t),x(t),x_{\tau }(t))dt+g(t,r(t),x(t),x_{\tau }(t))d\omega (t)$$

(5)

on $t\in [0,\mathrm{\infty })$ with the initial data given by

$$\{x(\theta ):-\overline{\tau }\le \theta \le 0\}=\xi \in L_{{\mathcal{L}}_0}^2([-\overline{\tau },0];R^n).$$

If $V\in C^{2,1}(R_{+}\times S\times R^n;R_{+})$, define an operator ℒ from $R_{+}\times S\times R^n$ to R by

$$\begin{array}{rl}\mathcal{L}V(t,i,x,x_{\tau })=& V_t(t,i,x)+V_x(t,i,x)f(t,i,x,x_{\tau })\\ +(1/2)trace(g^T(t,i,x,x_{\tau })V_{xx}(t,i,x)g(t,i,x,x_{\tau }))+\sum _{j=1}^N{\gamma }_{ij}V(t,j,x),\end{array}$$

where

$$\begin{array}{c}{V}_t(t,i,x)=\frac{\partial V(t,i,x)}{\partial t},\hfill \\ V_x(t,i,x)=(\frac{\partial V(t,i,x)}{\partial x_1},\frac{\partial V(t,i,x)}{\partial x_2},\dots ,\frac{\partial V(t,i,x)}{\partial x_n}),\hfill \\ V_{xx}(t,i,x)={\left(\frac{{\partial }^{2}V(t,i,x)}{\partial x_j\partial x_k}\right)}_{n\times n}.\hfill \end{array}$$

For the SDDE with Markovian switching, we have the Dynkin formula as follows.

Lemma 3 (Dynkin formula) [8, 28]

Let $V\in C^{2,1}(R_{+}\times S\times R^n;R_{+})$ and ${\tau }_1$, ${\tau }_2$ be bounded stopping times such that $0\le {\tau }_1\le {\tau }_2$ a.s. (i.e., almost surely). If $V(t,r(t),x(t))$ and $\mathcal{L}V(t,r(t),x(t),x_{\tau }(t))$ are bounded on $t\in [{\tau }_1,{\tau }_2]$ with probability 1, then

$$\mathcal{E}V({\tau }_2,r({\tau }_2),x({\tau }_2))=\mathcal{E}V({\tau }_1,r({\tau }_1),x({\tau }_1))+\mathcal{E}{\int }_{{\tau }_1}^{{\tau }_2}\mathcal{L}V(s,r(s),x(s),x_{\tau }(s))ds.$$

For the SDDE with Markovian switching again, the following hypothesis is imposed on the coefficients f and g.

Assumption 4 Both f and g satisfy the local Lipschitz condition. That is, for each $h>0$, there is an $L_h>0$ such that

$$|f(t,i,x,y)-f(t,i,\overline{x},\overline{y})|+|g(t,i,x,y)-g(t,i,\overline{x},\overline{y})|\le L_h(|x-\overline{x}|+|y-\overline{y}|)$$

for all $(t,i)\in R\times S$ and those $x,y,\overline{x},\overline{y}\in R^n$ with $x\vee y\vee \overline{x}\vee \overline{y}\le h$. Moreover,

$$sup\{|f(t,i,0,0)|\vee |g(t,i,0,0)|:t\ge 0,i\in S\}<\mathrm{\infty }.$$

Now we cite a useful result given by Yuan and Mao [29].

Lemma 4 [29]

Let Assumption  4 hold. Assume that there are functions $V\in C^{2,1}(R_{+}\times S\times R^n;R_{+})$, $\gamma \in L^1(R_{+};R_{+})$ and $w_1,w_2\in C(R^n;R_{+})$ such that

$$\mathcal{L}V(t,i,x,y)\le \gamma (t)-w_1(x)+w_2(y),\mathrm{\forall }(t,i,x,y)\in R_{+}\times S\times R^n\times R^n,$$

(6)

$$w_1(0)=w_2(0)=0,w_1(x)>w_2(x),\mathrm{\forall }x\ne 0$$

(7)

and

$$\underset{|x|\to \mathrm{\infty }}{lim}\underset{0\le t<\mathrm{\infty },i\in S}{inf}V(t,i,x)=\mathrm{\infty }.$$

(8)

Then the solution of Eq. (5) is almost surely asymptotically stable.

3 Main results

In this section, we give a criterion of the adaptive almost surely asymptotically synchronization for the drive system (1) and the response system (2).

Theorem 1 Assume that is a nonsingular M-matrix, where

$$\begin{array}{c}\eta =-2\gamma +\alpha +L^2+\beta +H_1,\hfill \\ \gamma =\underset{i\in S}{min}\underset{1\le j\le n}{min}{c}_j^i,\alpha =\underset{i\in S}{max}{\left(\rho \left(A^i\right)\right)}^2,\beta =\underset{i\in S}{max}{\left(\rho \left(B^i\right)\right)}^2,p\ge 2.\hfill \end{array}$$

Let $m>0$ and (in this case, ${(q_1,q_2,\dots ,q_N)}^T:=M^{-1}\overrightarrow{m}\gg 0$, i.e., all elements of $M^{-1}\overrightarrow{m}$ are positive by Lemma  1). Assume also that

$$(L^2+H_2)\overline{q}<-(\eta q_i+\sum _{k=1}^N{\gamma }_{ik}{q}_k),\mathrm{\forall }i\in S,$$

(9)

where $\overline{q}={max}_{i\in S}{q}_i$.

Under Assumptions 1∼3, the noise-perturbed response system (2) can be adaptive almost surely asymptotically synchronized with the delayed neural network (1) if the update law of the feedback control gain $K(t)$ of the controller (3) is chosen as

$${\dot{k}}_j=-q_i{\alpha }_j{e}_j^2,$$

(10)

where ${\alpha }_j>0$ ($j=1,2,\dots ,n$) are arbitrary constants.

Proof Under Assumptions 1∼3, it can be seen that the error system (4) satisfies Assumption 4.

For each $i\in S$, choose a nonnegative function as follows:

$$V(t,i,e)=q_i{|e|}^2+\sum _{j=1}^n\frac{1}{{\alpha }_j}{k}_j^2.$$

Then it is obvious that condition (8) holds.

Computing $\mathcal{L}V(t,i,e,e_{\tau })$ along the trajectory of the error system (4), and using (10), one can obtain that

$$\begin{array}{rl}\mathcal{L}V(t,i,e,e_{\tau })=& V_t+V_e[-C^{i}e+A^{i}g(e)+B^{i}g(e_{\tau })+U(t)]\\ +(1/2)trace({\sigma }^T(t,i,e,e_{\tau })V_{ee}\sigma (t,i,e,e_{\tau }))+\sum _{k=1}^N{\gamma }_{ik}V(t,k,e)\\ =& 2\sum _{j=1}^n\frac{1}{{\alpha }_j}{k}_j{\dot{k}}_j+2q_i{e}^T[-C^{i}e+A^{i}g(e)+B^{i}g(e_{\tau })+U(t)]\\ +q_{i}trace({\sigma }^T(t,i,e,e_{\tau })\sigma (t,i,e,e_{\tau }))+\sum _{k=1}^N{\gamma }_{ik}{q}_k{|e|}^2\\ =& 2q_i{e}^T[-C^{i}e+A^{i}g(e)+B^{i}g(e_{\tau })]\\ +q_{i}trace({\sigma }^T(t,i,e,e_{\tau })\sigma (t,i,e,e_{\tau }))+\sum _{k=1}^N{\gamma }_{ik}{q}_k{|e|}^2.\end{array}$$

(11)

Now, using Assumptions 1∼2 together with Lemma 2 yields

$$-e^T{C}^{i}e\le -\gamma {|e|}^2,$$

(12)

$$2e^T{A}^{i}g(e)\le e^T{A}^i{\left(A^i\right)}^{T}e+g^T(e)g(e)\le (\alpha +L^2){|e|}^2,$$

(13)

$$2e^T{B}^{i}g(e_{\tau })\le e^T{B}^i{\left(B^i\right)}^{T}e+g^T(e_{\tau })g(e_{\tau })\le \beta {|e|}^2+L^2{|e_{\tau }|}^2$$

(14)

and

$$q_{i}trace({\sigma }^T(t,i,e,e_{\tau })\sigma (t,i,e,e_{\tau }))\le q_i(H_1{|e|}^2+H_2{|e_{\tau }|}^2).$$

(15)

Substituting (12)∼(15) into (11) yields

$$\begin{array}{rl}\mathcal{L}V(t,i,e,e_{\tau })& \le (\eta q_i+\sum _{k=1}^N{\gamma }_{ik}{q}_k){|e|}^2+(L^2+H_2)q_i{|e_{\tau }|}^2\\ \le -m{|e|}^2+(L^2+H_2)\overline{q}{|e_{\tau }|}^2,\end{array}$$

(16)

where $m=-(\eta q_i+{\sum }_{k=1}^N{\gamma }_{ik}{q}_k)$ by ${(q_1,q_2,\dots ,q_N)}^T=M^{-1}\overrightarrow{m}$.

Let $w_1(e)=m{|e|}^2$, $w_2(e_{\tau })=(L^2+H_2)\overline{q}{|e_{\tau }|}^2$. Then inequalities (6) and (7) hold by using (9), where $\gamma (t)=0$ in (6). By Lemma 4, the error system (4) is adaptive almost surely asymptotically stable, and hence the noise-perturbed response system (2) can be adaptive almost surely asymptotically synchronized with the drive delayed neural network (1). This completes the proof. □

Remark 2 In Theorem 1, condition (9) of the adaptive almost surely asymptotically synchronization for the SDNN with Markovian switching obtained by using M-matrix and the Lyapunov functional method is generator-dependent and very different to other methods such as the linear matrix inequality method. And it is easy to check the condition if the drive system and the response system are given and the positive constant m is well chosen. To the best of the authors’ knowledge, this method is the first development in the research area of synchronization for neural networks.

Now, we are in a position to consider two special cases of the drive system (1) and the response system (2).

Special case 1 The Markovian jumping parameters are removed from the neural networks (1) and the response system (2). In this case, $N=1$ and the drive system, the response system and the error system can be represented, respectively, as follows:

$$dx(t)=[-Cx(t)+Af(x(t))+Bf\left(x(t-\tau (t))\right)+D]dt,$$

(17)

$$\begin{array}{c}dy(t)=[-Cy(t)+Af(y(t))+Bf\left(y(t-\tau (t))\right)+D+U(t)]dt\hfill \\ \phantom{dy(t)=}+\sigma (t,y(t)-x(t),y(t-\tau (t))-x(t-\tau (t)))d\omega (t)\hfill \end{array}$$

(18)

and

$$\begin{array}{rl}de(t)=& [-Ce(t)+Ag(e(t))+Bg(e_{\tau }(t))+U(t)]dt\\ +\sigma (t,e(t),e_{\tau }(t))d\omega (t).\end{array}$$

(19)

For this case, one can get the following result that is analogous to Theorem 1.

Corollary 1 Let

$$\begin{array}{c}\eta =-2\gamma +\alpha +L^2+\beta +H_1,\hfill \\ \gamma =\underset{1\le j\le n}{min}{c}_j,\alpha ={(\rho (A))}^2,\beta ={(\rho (B))}^2,p\ge 2.\hfill \end{array}$$

Assume that

$$\eta <0$$

and

$$L^2+H_2<-\eta .$$

(20)

Under Assumptions 1∼3, the noise-perturbed response system (18) can be adaptive almost surely asymptotically synchronized with the delayed neural network (17) if the update law of the feedback gain $K(t)$ of the controller (3) is chosen as

$${\dot{k}}_j=-{\alpha }_j{e}_j^2,$$

(21)

where ${\alpha }_j>0$ ($j=1,2,\dots ,n$) are arbitrary constants.

Proof Choose the following nonnegative function:

$$V(t,e)={|e|}^2+\sum _{j=1}^n\frac{1}{{\alpha }_j}{k}_j^2.$$

The rest of the proof is similar to that of Theorem 1, and hence omitted. □

Special case 2 The noise-perturbation is removed from the response system (2), which yields the noiseless response system

$$\begin{array}{rl}dy(t)=& [-\hat{C}(r(t))y(t)+\hat{A}(r(t))f(y(t))\\ +\hat{B}(r(t))f\left(y(t-\tau (t))\right)+D(r(t))+U(t)]dt\end{array}$$

(22)

and the error system

$$de(t)=[-C(r(t))e(t)+A(r(t))g(e(t))+B(r(t))g(e_{\tau }(t))+U(t)]dt,$$

(23)

respectively.

In this case, one can get the following results.

Corollary 2 Assume that is a nonsingular M-matrix, where

$$\eta =-2\gamma +\alpha +L^2+\beta .$$

Let $m>0$ and (in this case, ${(q_1,q_2,\dots ,q_N)}^T:=M^{-1}\overrightarrow{m}\gg 0$ by Lemma  1). Assume also that

$$L^2\overline{q}<-(\eta q_i+\sum _{k=1}^N{\gamma }_{ik}{q}_k),\mathrm{\forall }i\in S,$$

(24)

where $\overline{q}={max}_{i\in S}{q}_i$.

Under Assumptions 1∼3, the noiseless-perturbed response system (22) can be adaptive almost surely asymptotically synchronized with the unknown drive delayed neural network (1) if the update law of the feedback gain $K(t)$ of the controller (3) is chosen as

$${\dot{k}}_j=-q_i{\alpha }_j{e}_j^2,$$

(25)

where ${\alpha }_j>0$ are arbitrary constants.

Proof For each $i\in S$, choose a nonnegative function as follows:

$$V(t,i,e)=q_i{|e|}^2+\sum _{j=1}^n\frac{1}{{\alpha }_j}{k}_j^2.$$

The rest of the proof is similar to that of Theorem 1, and hence omitted. □

4 Numerical example

In the section, an illustrative example is given to support our main results.

Example 1 Consider a delayed neural network (1), and its response system (2) with Markovian switching and the following network parameters:

$$\begin{array}{c}{C}_1=\left[\begin{array}{cc}2& 0\\ 0& 2.4\end{array}\right],C_2=\left[\begin{array}{cc}1.5& 0\\ 0& 1\end{array}\right],A_1=\left[\begin{array}{cc}3.2& -1.5\\ -2.7& 3.2\end{array}\right],\hfill \\ A_2=\left[\begin{array}{cc}2.1& -0.6\\ -0.8& 3.2\end{array}\right],B_1=\left[\begin{array}{cc}2.7& -3.1\\ 0& 2.3\end{array}\right],B_2=\left[\begin{array}{cc}-1.4& -2.1\\ 0.3& 1.5\end{array}\right],\hfill \\ D_1=\left[\begin{array}{c}0.4\\ 0.5\end{array}\right],D_2=\left[\begin{array}{c}0.4\\ 0.6\end{array}\right],\Gamma =\left[\begin{array}{cc}-1.2& 1.2\\ 0.5& -0.5\end{array}\right],\hfill \\ \sigma (t,e(t),e(t-\tau ),1)={(0.4e_1(t-\tau ),0.5e_2(t))}^T,\hfill \\ \sigma (t,e(t),e(t-\tau ),2)={(0.5e_1(t),0.3e_2(t-\tau ))}^T,\hfill \\ f(x(t))=g(x(t))=tanh(x(t)),\tau =0.12,L=1.\hfill \end{array}$$

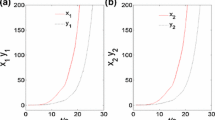
It can be checked that Assumption 1∼Assumption 3 and inequality (9) are satisfied and the matrix M is a nonsingular M-matrix. So, the noise-perturbed response system (2) can be adaptive almost surely asymptotically synchronized with the drive delayed neural network (1) by Theorem 1. The simulation results are given in Figures 1∼2. Figure 1 shows that the state response $e_1(t)$ and $e_2(t)$ of the errors system converge to zero. Figure 2 shows the dynamic curve of the feedback gain $k_1$ and $k_2$. From the simulations, it can be seen that the stochastic delayed neural networks with Markovian switching are adaptive almost surely asymptotically synchronization.

Figure 1

The response curve of the state variable ${\mathit{e}}_{\mathbf{1}}\mathbf{(}\mathit{t}\mathbf{)}$ and ${\mathit{e}}_{\mathbf{2}}\mathbf{(}\mathit{t}\mathbf{)}$ of the errors system.

Figure 2

The dynamic curve of the feedback gain ${\mathit{k}}_{\mathbf{1}}$ and ${\mathit{k}}_{\mathbf{2}}$ .

5 Conclusions

In this paper, we have proposed the concept of adaptive almost surely asymptotically synchronization for the stochastic delayed neural networks with Markovian switching. Making use of the M-matrix and Lyapunov functional method, we have obtained a sufficient condition, under which the response stochastic delayed neural network with Markovian switching can be adaptive almost surely asymptotically synchronized with the drive delayed neural networks with Markovian switching. The method to obtain the sufficient condition of the adaptive synchronization for neural networks is different to that of the linear matrix inequality technique. The condition obtained in this paper is dependent on the generator of the Markovian jumping models and can be easily checked. Extensive simulation results are provided to demonstrate the effectiveness of our theoretical results and analytical tools.