Abstract
This paper is concerned with the p th moment exponential stability of fuzzy cellular neural networks with time-varying delays under impulsive perturbations and stochastic noises. Based on the Lyapunov function, stochastic analysis and differential inequality technique, a set of novel sufficient conditions on p th moment exponential stability of the system are derived. These results generalize and improve some of the existing ones. Moreover, an illustrative example is given to demonstrate the effectiveness of the results obtained.
Similar content being viewed by others
1 Introduction
In the last decades, cellular neural networks [1, 2] have been extensively studied and applied in many different fields such as associative memory, signal processing and some optimization problems. In such applications, it is of prime importance to ensure that the designed neural networks are stable. In practice, due to the finite speeds of the switching and transmission of signals, time delays do exist in a working network and thus should be incorporated into the model equation. In recent years, the dynamical behaviors of cellular neural networks with constant delays or time-varying delays or distributed delays have been studied; see, for example, [3–11] and the references therein.
In addition to the delay effects, recently, studies have been intensively focused on stochastic models. It has been realized that the synaptic transmission is a noisy process brought on by random fluctuations from the release of neurotransmitters and other probabilistic causes, and it is of great significance to consider stochastic effects on the stability of neural networks or dynamical system described by stochastic functional differential equations (see [12–23]). On the other hand, most neural networks can be classified as either continuous or discrete. Therefore most of the investigations focused on the continuous or discrete systems, respectively. However, there are many real-world systems and neural processes that behave in piecewise continuous style interlaced with instantaneous and abrupt change (impulses). Motivated by this fact, several new neural networks with impulses have been recently proposed and studied (see [24–33]).
In this paper, we would like to integrate fuzzy operations into cellular neural networks. Speaking of fuzzy operations, Yang and Yang [34] first introduced fuzzy cellular neural networks (FCNNs) combining those operations with cellular neural networks. So far researchers have found that FCNNs are useful in image processing, and some results have been reported on stability and periodicity of FCNNs [34–40]. However, to the best of our knowledge, few author investigated the stability of stochastic fuzzy cellular neural networks with time-varying delays and impulses.
Motivated by the above discussions, in this paper, we consider the following stochastic fuzzy cellular neural networks with time-varying delays and impulses
where n corresponds to the number of units in the neural networks. For , corresponds to the state of the i th neuron. , are signal transmission functions. denotes the rate at which a cell i resets its potential to the resting state when isolated from other cells and inputs; corresponds to the transmission delay. represents the elements of the feedback template. , , , and are elements of fuzzy feedback MIN template and fuzzy feedback MAX template, fuzzy feed-forward MIN template and fuzzy feed-forward MAX template, respectively; ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operation, respectively; denotes the external input of the i th neurons. is the external bias of the i th unit. is a transmission delay satisfying ; is the diffusion coefficient matrix and is the i th row vector of : is an n-dimensional Brownian motion defined on a complete probability space with a filtration satisfying the usual conditions (i.e., it is right continuous and contains all P-null sets). is the impulses at moment , the fixed moments of time satisfy , ; , .
System (1) is supplemented with the initial condition given by
where is -measurable and continuous everywhere except at a finite number of points , at which and exist and .
Let denote the family of all nonnegative functions on which are continuous once differentiable in t and twice differentiable in x. If , define an operator LV associated with (1) as
where
For convenience, we introduce several notations. denotes a column vector. denotes a vector norm defined by ; denotes the space of continuous mappings from topological space X to topological space Y. Denoted by is the family of all bounded -measurable, -valued random variables ϕ, satisfying , where denotes the expectation of a stochastic process.
Throughout the paper, we give the following assumptions.
(A1) The signal transmission functions , () are Lipschitz continuous on R with Lipschitz constants and , namely, for any ,
(A2) There exist non-negative numbers , such that for all , ,
(A3) , where is the equilibrium point of (1) with the initial condition (2), satisfies .
Definition 1.1 The equilibrium point of system (1) is said to be p th moment exponentially stable if there exist positive constants , such that
where is any solution of system (1) with initial value , .
When , it is usually said to be exponentially stable in mean square.
Lemma 1.1 [34]
Suppose x and y are two states of system (1), then we have
and
Lemma 1.2 If () denote p nonnegative real numbers, then
where denotes an integer. A particular form of (4), namely
2 Main results
In this section, we consider the existence and global p th moment exponential stability of system (1).
Lemma 2.1 For two positive real numbers a and b, assume that there exists a constant number such that . Then the equation
has a unique solution .
Proof Let . It is easy to see , , . Thus, is strictly increasing on . Therefore, Eq. (5) has a unique positive solution . □
Lemma 2.2 [18]
For two positive real numbers a and b, assume that there exists a constant number such that . Assume that is a nonnegative continuous function on and satisfies the following inequality:
then , where λ is a solution of (5) and the upper right Dini derivative of is defined as
Theorem 2.1 Under conditions (A1)-(A3), if there exist constants (), such that
where
Then is a unique equilibrium which is globally pth moment exponential stable.
Proof The proof of existence and uniqueness of equilibrium for the system is similar to that of [39]. So we omit it. Suppose that is the unique equilibrium of system (1).
Let
then system (1) can be transformed into the following equation, for :
We define a Lyapunov function . Let , , then we can get the operator associated with system (8) of the following form:
where
Firstly, for , applying the Ito formula, we obtain that
Since , taking expectations on both sides of equality (10) and applying the inequality (9) yields
Since the Dini derivative is
denote , the preceding result (11) leads directly to
Hence, from Lemma 2.2, we have
Namely,
where , λ is the unique positive solution of the following equation:
Next, suppose that for , the inequality
holds. From (A3), we get
This, together with (14), leads to
On the other hand, for , applying the Ito formula, we get
Then, we have
So, for small enough , we have
From (16) and (17), we have
Similarly, we obtain
Hence, by the mathematical induction, for any , we conclude that
which implies that the equilibrium point of the impulsive system (1) is p th moment exponentially stable. This completes the proof of the theorem. □
3 Comparisons and remarks
It can be easily seen that many neural networks are special cases of system (1). Thus, in this section, we give some comparisons and remarks.
Suppose that , system (1) becomes the stochastic fuzzy cellular neural networks with time-varying delays.
For (20), we have the following corollary by Theorem 2.1.
Corollary 3.1 If (A1)-(A2) hold, if there exist constants (), such that
where
then the unique equilibrium of system (20) is globally pth moment exponential stable.
If we do not consider fuzzy AND and fuzzy OR operations and when in system (1), then system (1) becomes impulsive stochastic cellular neural networks with time-varying delays
Remark 3.1 The stability of system (21) has been investigated in [31]. In [31], authors required the differentiability and monotonicity of a time delays function which satisfied . Hence, this assumption may impose a very strict constraint on the model because time delays sometimes vary dramatically with time in real circuits. Obviously, Theorem 2.1 does not require these conditions.
Remark 3.2 In Theorem 2.1, if we do not consider fuzzy AND and OR operation, it becomes traditional cellular neural networks. The results in [32] are the corollary of Theorem 2.1. Therefore the results of this paper extend the previous known publication.
4 An example
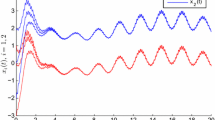
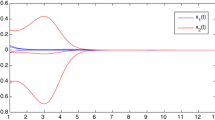
Example 4.1 Consider the following stochastic fuzzy neural networks with time-varying delays and time-varying delays and impulses
where , , , and
and ().
Let , obviously, , . By simple computation, we can easily get that , . Letting , we have
Thus, system (22) satisfies assumptions (A1)-(A3). It follows from Theorem 2.1 that system (22) is exponentially stable in mean square.
References
Chua LO, Yang L: Cellular neural networks: theory. IEEE Trans. Circuits Syst. 1988, 35: 1257-1272. 10.1109/31.7600
Chua LO, Yang L: Cellular neural networks: applications. IEEE Trans. Circuits Syst. 1988, 35: 1273-1290. 10.1109/31.7601
Zhao H, Cao J: New conditions for global exponential stability of cellular neural networks with delays. Neural Netw. 2005, 18: 1332-1340. 10.1016/j.neunet.2004.11.010
Cao J, Chen T: Globally exponentially robust stability and periodicity of delayed neural networks. Chaos Solitons Fractals 2004, 4: 957-963.
Chen Y: Network of neurons with delayed feedback: periodical switching of excitation and inhibition. Dyn. Contin. Discrete Impuls. Syst., Ser. B, Appl. Algorithms 2007, 14: 113-122.
Huang C, Huang L: Dynamics of a class of Cohen-Grossberg neural networks with time-varying delays. Nonlinear Anal., Real World Appl. 2007, 8: 40-52. 10.1016/j.nonrwa.2005.04.008
Wu Y, Li T, Wu Y: Improved exponential stability criteria for recurrent neural networks with time-varying discrete and distributed delays. Int. J. Autom. Comput. 2010, 7: 199-204. 10.1007/s11633-010-0199-z
Liu Z, Chen A, Cao J, Huang L: Existence and global exponential stability of periodic solution for BAM neural networks with periodic coefficients and time-varying delays. IEEE Trans. Circuits Syst. I 2003, 50: 1162-1173. 10.1109/TCSI.2003.816306
Jiang H, Teng Z: Global exponential stability of cellular neural networks with time-varying coefficients and delays. Neural Netw. 2004, 17: 1415-1425. 10.1016/j.neunet.2004.03.002
Huang T, Cao J, Li C: Necessary and sufficient condition for the absolute exponential stability of a class of neural networks with finite delay. Phys. Lett. A 2006, 352: 94-98. 10.1016/j.physleta.2005.11.038
Li X, Huang L, Zhu H: Global stability of cellular neural networks with constant and variable delays. Nonlinear Anal. 2003, 53: 319-333. 10.1016/S0362-546X(02)00176-1
Huang C, He Y, Huang L, Zhu W: p th moment stability analysis of stochastic recurrent neural networks with time-varying delays. Inf. Sci. 2008, 178: 2194-2203. 10.1016/j.ins.2008.01.008
Huang C, Cao J: Almost sure exponential stability of stochastic cellular neural networks with unbounded distributed delays. Neurocomputing 2009, 72: 3352-3356. 10.1016/j.neucom.2008.12.030
Sun Y, Cao J: p th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Anal., Real World Appl. 2007, 8: 1171-1185. 10.1016/j.nonrwa.2006.06.009
Wu S, Li C: Exponential stability of impulsive discrete systems with time delay and applications in stochastic neural networks: a Razumikhin approach. Neurocomputing 2012, 82: 29-36.
Li X, Fu X: Synchronization of chaotic delayed neural networks with impulsive and stochastic perturbations. Commun. Nonlinear Sci. Numer. Simul. 2011, 16: 885-894. 10.1016/j.cnsns.2010.05.025
Park J, Kwon O: Analysis on global stability of stochastic neural networks of neutral type. Mod. Phys. Lett. B 2008, 20: 3159-3170.
Huang C, He Y, Chen P: Dynamic analysis of stochastic recurrent neural networks. Neural Process. Lett. 2008, 27: 267-276. 10.1007/s11063-008-9075-z
Shatyrko A, Diblik J, Khusainov D, Ruzaickova M: Stabilization of Lur’e-type nonlinear control systems by Lyapunov-Krasovskii functionals. Adv. Differ. Equ. 2012., 2012: Article ID 229
Diblik J, Dzhalladova I, Ruzaickova M: The stability of nonlinear differential systems with random parameters. Abstr. Appl. Anal. 2012., 2012: Article ID 924107 10.1155/2012/924107
Dzhalladova I, Bastinec J, Diblik J, Khusainov D: Estimates of exponential stability for solutions of stochastic control systems with delay. Abstr. Appl. Anal. 2011., 2011: Article ID 920412 10.1155/2011/920412
Diblik J, Khusainov D, Grytsay I, Smarda Z: Stability of nonlinear autonomous quadratic discrete systems in the critical case. Discrete Dyn. Nat. Soc. 2010., 2010: Article ID 539087 10.1155/2010/539087
Khusainov D, Diblik J, Svoboda Z, Smarda Z: Instable trivial solution of autonomous differential systems with quadratic right-hand sides in a cone. Abstr. Appl. Anal. 2011., 2011: Article ID 154916 10.1155/2011/154916
Bai C: Stability analysis of Cohen-Grossberg BAM neural networks with delays and impulses. Chaos Solitons Fractals 2008, 35: 263-267. 10.1016/j.chaos.2006.05.043
Guan Z, James L, Chen G: On impulsive auto-associative neural networks. Neural Netw. 2000, 13: 63-69. 10.1016/S0893-6080(99)00095-7
Guan Z, Chen G: On delayed impulsive Hopfield neural networks. Neural Netw. 1999, 12: 273-280. 10.1016/S0893-6080(98)00133-6
Li Y: Globe exponential stability of BAM neural networks with delays and impulses. Chaos Solitons Fractals 2005, 24: 279-285.
Zhang Y, Sun J: Stability of impulsive neural networks with time delays. Phys. Lett. A 2005, 348: 44-50. 10.1016/j.physleta.2005.08.030
Chen Z, Ruan J: Global dynamic analysis of general Cohen-Grossberg neural networks with impulse. Chaos Solitons Fractals 2007, 32: 1830-1837. 10.1016/j.chaos.2005.12.018
Song Q, Zhang J: Global exponential stability of impulsive Cohen-Grossberg neural network with time-varying delays. Nonlinear Anal., Real World Appl. 2008, 9: 500-510. 10.1016/j.nonrwa.2006.11.015
Sun Y, Cao J: p th moment exponential stability of stochastic recurrent neural networks with time-varying delays. Nonlinear Anal., Real World Appl. 2007, 8: 1171-1185. 10.1016/j.nonrwa.2006.06.009
Li X, Zou J, Zhu E: The p th moment exponential stability of stochastic cellular neural networks with impulses. Adv. Differ. Equ. 2013., 2013: Article ID 6
Song Q, Wang Z: Stability analysis of impulsive stochastic Cohen-Grossberg neural networks with mixed time delays. Physica A 2008, 387: 3314-3326. 10.1016/j.physa.2008.01.079
Yang T, Yang L: The global stability of fuzzy cellular neural networks. IEEE Trans. Circuits Syst. I 1996, 43: 880-883. 10.1109/81.538999
Yang T, Yang L, Wu C, Chua L: Fuzzy cellular neural networks: theory. In Proc. IEEE Int. Workshop Cellular Neural Networks Appl.. Edited by: Circuits I, Society S. IEEE Press, New York; 1996:181-186.
Yang T, Yang L, Wu C, Chua L: Fuzzy cellular neural networks: applications. In Proc. IEEE Int. Workshop Cellular Neural Networks Appl.. Edited by: Circuits I, Society S. IEEE Press, New York; 1996:225-230.
Huang T: Exponential stability of fuzzy cellular neural networks with distributed delay. Phys. Lett. A 2006, 351: 48-52. 10.1016/j.physleta.2005.10.060
Huang T: Exponential stability of delayed fuzzy cellular neural networks with diffusion. Chaos Solitons Fractals 2007, 31: 658-664. 10.1016/j.chaos.2005.10.015
Zhang Q, Yang L: Exponential p -stability of impulsive stochastic fuzzy cellular neural networks with mixed delays. WSEAS Trans. Math. 2011, 12: 490-499.
Yuan K, Cao J, Deng J: Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays. Neurocomputing 2006, 69: 1619-1627. 10.1016/j.neucom.2005.05.011
Acknowledgements
The authors would like to thank the editor and the referees for their helpful comments and valuable suggestions regarding this paper. This work is partially supported by 973 program (2009CB326202), the National Natural Science Foundation of China (11071060, 60835004, 11101133), Fundamental Research Fund for the Central Universities of China (531107040222) and Scientific Research Fund of Hunan Provincial Education Department (Grant No. 12A206).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors indicated in parentheses made substantial contributions to the following tasks of research: drafting the manuscript (PX); participating in the design of the study (LH); writing of paper (PX).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xiong, P., Huang, L. On p th moment exponential stability of stochastic fuzzy cellular neural networks with time-varying delays and impulses. Adv Differ Equ 2013, 172 (2013). https://doi.org/10.1186/1687-1847-2013-172
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-172