FDM for fractional parabolic equations with the Neumann condition

Abstract

In the present study, the first and second order of accuracy stable difference schemes for the numerical solution of the initial boundary value problem for the fractional parabolic equation with the Neumann boundary condition are presented. Almost coercive stability estimates for the solution of these difference schemes are obtained. The method is illustrated by numerical examples.

MSC:34K37, 35R11, 35B35, 39A14, 47B48.

1 Introduction

Mathematical modeling of fluid mechanics (dynamics, elasticity) and other areas of physics lead to fractional partial differential equations. Numerical methods and theory of solutions of the problems for fractional differential equations have been studied extensively by many researchers (see, e.g., [1–31] and the references given therein).

The method of operators as a tool for investigation of the well-posedness of boundary value problems for parabolic partial differential equations is well known (see, e.g., [32–41]). In paper [42], the initial value problem

$$\frac{du(t)}{dt}+D_t^{\frac{1}{2}}u(t)+Au(t)=f(t),0<t<T,u(0)=0$$

(1.1)

for the fractional differential equation in a Banach space E with the strongly positive operator A was investigated. This fractional differential equation corresponds to the Basset problem [43]. It represents a classical problem in fluid dynamics where the unsteady motion of a particle accelerates in a viscous fluid due to the gravity of force. Here $D_t^{\frac{1}{2}}=D_{0+}^{\frac{1}{2}}$ is the standard Riemann-Liouville’s derivative of order $\frac{1}{2}$.

The well-posedness of (1.1) in spaces of smooth functions was established. The coercive stability estimates for the solution of the 2m th order multidimensional fractional parabolic equation and the one-dimensional fractional parabolic equation with nonlocal boundary conditions in space variable were obtained.

In paper [44], the stable first order of accuracy difference scheme for the approximate solution of initial value problem (1.1)

$$\{\begin{array}{l}{\tau }^{-1}(u_k-u_{k-1})+A{u}_k+D_{\tau }^{\frac{1}{2}}{u}_k=f_k,\\ f_k=f(t_k),t_k=k\tau ,1\le k\le N,N\tau =T,u_0=0\end{array}$$

(1.2)

was presented. Here (see, [45]),

$$\begin{array}{r}{D}_{\tau }^{\frac{1}{2}}{u}_k=\frac{1}{\sqrt{\pi }}\sum _{m=1}^k\frac{\mathrm{\Gamma }(k-m+\frac{1}{2})}{(k-m)!}\frac{u_m-u_{m-1}}{{\tau }^{\frac{1}{2}}},\\ \mathrm{\Gamma }(k-m+\frac{1}{2})={\int }_0^{\mathrm{\infty }}{t}^{k-m-\frac{1}{2}}{e}^{-t}dt.\end{array}$$

(1.3)

Let $F_{\tau }(E)$ be the linear space of mesh functions ${\phi }^{\tau }={\{{\phi }_k\}}_1^N$ with values in the Banach space E. Next, on $F_{\tau }(E)$ we introduce the Banach space $C_{\tau }(E)=C({[0,T]}_{\tau },E)$ with the norm

$${\parallel {\phi }^{\tau }\parallel }_{C_{\tau }(E)}=\underset{1\le k\le N}{max}{\parallel {\phi }_k\parallel }_E.$$

The well-posedness of (1.2) in difference analogues of spaces of smooth functions was established. Namely, we have the following theorems.

Theorem 1.1 Let A be a strongly positive operator in a Banach space E. Then, for the solution $u^{\tau }={\{u_k\}}_1^N$ in $C_{\tau }(E)$ of initial value problem (1.2) the stability inequality holds:

$${\parallel {\left\{D_{\tau }^{\frac{1}{2}}{u}_k\right\}}_1^N\parallel }_{C_{\tau }(E)}+{\parallel {\{{\tau }^{-1}(u_k-u_{k-1})+A{u}_k\}}_1^N\parallel }_{C_{\tau }(E)}\le M{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}.$$

(1.4)

Theorem 1.2 Let A be a strongly positive operator in a Banach space E. Then, for the solution $u^{\tau }={\{u_k\}}_1^N$ in $C_{\tau }(E)$ of initial value problem (1.2) the almost coercive stability inequality is valid:

$$\begin{array}{r}{\parallel {\{{\tau }^{-1}(u_k-u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}+{\parallel {\{A{u}_k\}}_1^N\parallel }_{C_{\tau }(E)}\\ \le Mmin\{ln\frac{1}{\tau },1+ln{\parallel A\parallel }_{E\to E}\}{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}.\end{array}$$

(1.5)

Here, and in future, positive constants, which can differ in time (hence: not a subject of precision) will be indicated with an M. On the other hand $M(\alpha ,\beta ,\dots )$ is used to focus on the fact that the constant depends only on $\alpha ,\beta ,\dots$ .

Finally, the coercive stability and almost coercive stability estimates for the solution of difference schemes the first order of approximation in t for the 2m th order multidimensional fractional parabolic equation and the one-dimensional fractional parabolic equation with nonlocal boundary conditions in space variable were obtained.

In the present paper, applying the second order of approximation formula

$$D_{\tau }^{1/2}{u}_k=\{\begin{array}{ll}-d\sqrt{2}/3u_0+d\sqrt{2}/3u_1,& k=1,\\ 2d\sqrt{6}/5u_0+d\sqrt{6}/5u_1+d\sqrt{6}/5u_2,& k=2,\\ d{\sum }_{m=2}^{k-1}\{[(k-m)\lambda (k-m)+\mu (k-m)]u_{m-2}\\ +[(2m-2k-1)\lambda (k-m)-2\mu (k-m)]u_{m-1}\\ +[(k-m+1)\lambda (k-m)+\mu (k-m)]u_m\}\\ +\frac{d}{6\sqrt{2}}[-u_{k-2}-4u_{k-1}+5u_k],& 3\le k\le N\end{array}$$

(1.6)

for

$$D_t^{1/2}u(t_k-\tau /2)=\frac{1}{\mathrm{\Gamma }(1/2)}{\int }_0^{t_k-\tau /2}{(t_k-\tau /2-s)}^{-1/2}{u}^{\mathrm{\prime }}(s)ds,$$

and using the Crank-Nicholson difference scheme for parabolic equations, we present the second order of accuracy difference scheme

$$\{\begin{array}{l}{\tau }^{-1}(u_k-u_{k-1})+\frac{1}{2}A(u_k+u_{k-1})+D_{\tau }^{\frac{1}{2}}{u}_k=f_k,\\ f_k=f(t_k-\frac{\tau }{2}),t_k=k\tau ,1\le k\le N,N\tau =T,u_0=0\end{array}$$

(1.7)

for the approximate solution of initial value problem (1.1). Here,

$$\begin{array}{r}d=\frac{2}{\sqrt{\pi \tau }},\lambda (r)=\sqrt{r+1/2}-\sqrt{r-1/2},\\ \mu (r)=-\frac{1}{3}({(r+1/2)}^{3/2}-{(r-1/2)}^{3/2}).\end{array}$$

The well-posedness of (1.7) in $C_{\tau }(E)$ is established. In applications, the initial boundary value problem for the fractional parabolic equation

$$\{\begin{array}{l}\frac{\partial u(t,x)}{\partial t}+D_t^{1/2}u(t,x)-{\sum }_{p=1}^m{a}_p(x)\frac{{\partial }^{2}u(t,x)}{\partial x_p^2}+{\sum }_{p=1}^m{b}_p(x)\frac{\partial u(t,x)}{\partial x_p}+\sigma u(t,x)=f(t,x),\\ x=(x_1,\dots ,x_m)\in \mathrm{\Omega },0<t<T,\\ \frac{\partial u(t,x)}{\partial \overrightarrow{n}}=0,x\in S,0\le t\le T,\\ u(0,x)=0,x\in \overline{\mathrm{\Omega }}\end{array}$$

(1.8)

is considered. Here, Ω is the open cube in the m-dimensional Euclidean space

$${\mathbb{R}}^m:\{x\in \mathrm{\Omega }:x=(x_1,\dots ,x_m);0<x_j<1,1\le j\le m\}$$

with boundary S, $\overline{\mathrm{\Omega }}=\mathrm{\Omega }\cup S$, $a_p(x)$ and $b_p(x)$ ($x\in \mathrm{\Omega }$) and $f(t,x)$ ($t\in (0,T)$, $x\in \mathrm{\Omega }$) are given smooth functions and $a_p(x)\ge a>0$, $\sigma >0$ and $\overrightarrow{n}$ is the normal vector to S.

The first and second order of accuracy difference schemes for the approximate solution of problem (1.8) are presented. The almost coercive stability estimates for the solution of these difference schemes are established. The theoretical statements for the solution of these difference schemes for one-dimensional fractional parabolic equations are supported by numerical examples.

2 The well-posedness of difference scheme

It is clear that the following representation formula

$$u_k=-\sum _{s=1}^k{B}^{k-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^k{B}^{k-s}C{f}_s\tau ,1\le k\le N$$

(2.1)

holds for the solution of problem (1.7). Here, $C={(I+\frac{\tau A}{2})}^{-1}$ and $B=(I-\frac{\tau A}{2})C$.

Theorem 2.1 Let A be a strongly positive operator in a Banach space E. Then, for the solution $u^{\tau }={\{u_k\}}_1^N$ in $C_{\tau }(E)$ of initial value problem (1.2) the following stability inequality holds:

$${\parallel {\left\{D_{\tau }^{\frac{1}{2}}{u}_k\right\}}_1^N\parallel }_{C_{\tau }(E)}+{\parallel {\{{\tau }^{-1}(u_k-u_{k-1})+\frac{A}{2}(u_k+u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}\le M{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}.$$

(2.2)

Proof Using formulas (2.1) and (1.6), we get

$$\begin{array}{r}{D}_{\tau }^{\frac{1}{2}}{u}_1=d\sqrt{2}/3\{-C{D}_{\tau }^{\frac{1}{2}}{u}_1\tau +C{f}_1\tau \},\\ D_{\tau }^{\frac{1}{2}}{u}_2=d\sqrt{6}/5\{-C^2{D}_{\tau }^{\frac{1}{2}}{u}_1\tau -\frac{C}{2}{D}_{\tau }^{\frac{1}{2}}{u}_2\tau +C^2{f}_1\tau +\frac{C}{2}{f}_2\tau \},\\ D_{\tau }^{\frac{1}{2}}{u}_k=d\sum _{m=2}^{k-1}\{[(k-m)\lambda (k-m)+\mu (k-m)]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}\times [-\sum _{s=1}^{m-2}{B}^{m-2-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^{m-2}{B}^{m-2-s}C{f}_s\tau ]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}+[(2m-2k-1)\lambda (k-m)-2\mu (k-m)]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}\times [-\sum _{s=1}^{m-1}{B}^{m-1-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^{m-1}{B}^{m-1-s}C{f}_s\tau ]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}+[(k-m+1)\lambda (k-m)+\mu (k-m)]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}\times [-\sum _{s=1}^m{B}^{m-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^m{B}^{m-s}C{f}_s\tau ]\}\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}+\frac{d}{6\sqrt{2}}\{-[-\sum _{s=1}^{k-2}{B}^{k-2-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^{k-2}{B}^{k-2-s}C{f}_s\tau ]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}-4[-\sum _{s=1}^{k-1}{B}^{k-1-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^{k-1}{B}^{k-1-s}C{f}_s\tau ]\\ \phantom{D_{\tau }^{\frac{1}{2}}{u}_k=}+5[-\sum _{s=1}^k{B}^{k-s}C{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\sum _{s=1}^k{B}^{k-s}C{f}_s\tau ]\},3\le k\le N.\end{array}$$

(2.3)

Now, let us first estimate $z_k={\parallel D_{\tau }^{\frac{1}{2}}{u}_k\parallel }_E$ for any $1\le k\le N$. Using formula (2.3) and the estimate

$${\parallel C\parallel }_{E\to E}\le M,$$

(2.4)

we get

(2.5)

(2.6)

Now we consider the case $3\le k\le N$. Applying formula (2.3), the triangle inequality and estimates [46]

$${\parallel A{B}^k{C}^2\parallel }_{E\to E}\le \frac{M}{k\tau },{\parallel B^{k}C\parallel }_{E\to E}\le M,1\le k\le N,$$

(2.7)

we get

$$z_k\le M_3\sum _{s=1}^{k-1}\frac{1}{\sqrt{(k-s)\tau }}\tau (z_s+{\parallel f_s\parallel }_E)+M_4(z_k+{\parallel f_k\parallel }_E){\tau }^{\frac{1}{2}}.$$

(2.8)

Applying the difference analogue of the integral inequality and inequalities (2.5), (2.6) and (2.8), we get

$${\parallel {\left\{D_{\tau }^{\frac{1}{2}}{u}_k\right\}}_1^N\parallel }_{C_{\tau }(E)}={\parallel {\{z_k\}}_1^N\parallel }_{C_{\tau }(E)}\le M{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}.$$

(2.9)

Using the triangle inequality and equation (1.2), we get

$$\begin{array}{rcl}{\parallel {\{{\tau }^{-1}(u_k-u_{k-1})+\frac{A}{2}(u_k+u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}& \le & [{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}+{\parallel {\left\{D_{\tau }^{\frac{1}{2}}{u}_k\right\}}_1^N\parallel }_{C_{\tau }(E)}]\\ \le & M_1{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}.\end{array}$$

(2.10)

Estimate (2.2) follows from estimates (2.9) and (2.10). Theorem 2.1 is proved. □

Theorem 2.2 Let A be a strongly positive operator in a Banach space E. Then, for the solution $u^{\tau }={\{u_k\}}_1^N$ in $C_{\tau }(E)$ of initial value problem (1.2) the almost coercive stability inequality is valid:

$$\begin{array}{r}{\parallel {\{{\tau }^{-1}(u_k-u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}+{\parallel {\{\frac{A}{2}(u_k+u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}\\ \le Mmin\{ln\frac{1}{\tau },1+ln{\parallel A\parallel }_{E\to E}\}{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}.\end{array}$$

(2.11)

Proof Using formula (2.1), we get

$$\begin{array}{r}{\tau }^{-1}(u_k-u_{k-1})\\ =-\frac{C}{2}{D}_{\tau }^{\frac{1}{2}}{u}_k-\sum _{s=1}^{k-1}A{B}^{k-1-s}{C}^2{D}_{\tau }^{\frac{1}{2}}{u}_s\tau +\frac{C}{2}{f}_k+\sum _{s=1}^{k-1}A{B}^{k-1-s}{C}^2{f}_s\tau .\end{array}$$

(2.12)

The proof of estimate

$${\parallel {\{{\tau }^{-1}(u_k-u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}\le Mmin\{ln\frac{1}{\tau },1+ln{\parallel A\parallel }_{E\to E}\}{\parallel f^{\tau }\parallel }_{C_{\tau }(E)}$$

(2.13)

for the solution of initial value problem (1.2) is based on formula (2.12) and estimate (2.2) and the following estimates [46]:

$$\begin{array}{r}\underset{1\le k\le N}{max}{\parallel \frac{C}{2}{f}_k+\sum _{s=1}^{k-1}A{B}^{k-1-s}{C}^2{f}_s\tau \parallel }_E\\ \le Mmin\{ln\frac{1}{\tau },1+ln{\parallel A\parallel }_{E\to E}\}{\parallel f^{\tau }\parallel }_{C(E)},\\ \underset{1\le k\le N}{max}{\parallel \frac{C}{2}{f}_k+\sum _{s=1}^{k-1}A{B}^{k-1-s}{C}^2{D}_{\tau }^{\frac{1}{2}}{u}_s\tau \parallel }_E\\ \le Mmin\{ln\frac{1}{\tau },1+ln{\parallel A\parallel }_{E\to E}\}{\parallel {\left\{D_{\tau }^{\frac{1}{2}}{u}_k\right\}}_1^N\parallel }_{C(E)}.\end{array}$$

Using these estimates, the triangle inequality and equation (1.2), we get

$${\parallel {\{\frac{A}{2}(u_k+u_{k-1})\}}_1^N\parallel }_{C_{\tau }(E)}\le M_{1}min\{ln\frac{1}{\tau },1+ln{\parallel A\parallel }_{E\to E}\}{\parallel f^{\tau }\parallel }_{C(E)}.$$

(2.14)

Estimate (2.11) follows from estimates (2.13) and (2.14). Theorem 2.2 is proved. □

3 Applications

Now, we consider the applications of Theorems 2.1 and 2.2 to initial boundary value problem (1.8). The discretization of problem (1.8) is carried out in two steps. In the first step, let us define the grid space

$$\{\begin{array}{l}{\overline{\mathrm{\Omega }}}_h=\{x=x_p=(h_1{p}_1,\dots ,h_m{p}_m),p=(p_1,\dots ,p_m),\\ \phantom{{\overline{\mathrm{\Omega }}}_h=}0\le p_j\le M_j,h_j{M}_j=1,j=1,\dots ,m\},\\ {\mathrm{\Omega }}_h={\overline{\mathrm{\Omega }}}_h\cap \mathrm{\Omega },S_h={\overline{\mathrm{\Omega }}}_h\cap S.\end{array}$$

We introduce the Banach space $C_h=C({\overline{\mathrm{\Omega }}}_h)$ of the grid function ${\phi }^h(x)=\{\phi (h_1{p}_1,\dots ,h_m{p}_m)\}$ defined on $\overline{\mathrm{\Omega }}$, equipped with the norm

$${\parallel {\phi }^h\parallel }_{C({\overline{\mathrm{\Omega }}}_h)}=\underset{x\in {\overline{\mathrm{\Omega }}}_h}{max}|{\phi }^h(x)|.$$

To the differential operator $A^x$ generated by problem (1.8), we assign the difference operator $A_h^x$ by the formula

$$A_h^x{u}^h(x)=-\sum _{p=1}^m{a}_p(x)u_{\overline{x}{x}_p,j_p}^h(x)+\sum _{p=1}^m{b}_p(x)u_{\stackrel{\circ }{x},j_p}^h(x)+\sigma u^h(x)$$

acting in the space of grid functions $u^h(x)$, satisfying the conditions $D^h{u}^h(x)=0$ for all $x\in S_h$. Here, $D^h{u}^h(x)$ is the first or second order of approximation of $\frac{\partial u}{\partial \overrightarrow{n}}$. It is known that (see, [47, 48]) $A_h^x$ is a strongly positive definite operator in $C({\overline{\mathrm{\Omega }}}_h)$. With the help of $A_h^x$ we arrive at the initial boundary value problem

$$\{\begin{array}{l}\frac{d{v}^h(t,x)}{dt}+D_t^{1/2}{v}^h(t,x)+A_h^x{v}^h(t,x)=f^h(t,x),0<t<T,x\in {\mathrm{\Omega }}_h,\\ v^h(0,x)=0,x\in \overline{\mathrm{\Omega }}\end{array}$$

(3.1)

for a finite system of ordinary fractional differential equations.

In the second step, applying the first order of approximation formula defined by (1.3) for

$$D_t^{1/2}u(t_k)=\frac{1}{\mathrm{\Gamma }(1/2)}{\int }_0^{t_k}{(t_k-s)}^{-1/2}{u}^{\mathrm{\prime }}(s)ds$$

and using the first order of accuracy stable difference scheme for parabolic equations, we can present the first order of accuracy difference scheme

$$\{\begin{array}{l}\frac{u_k^h(x)-u_{k-1}^h(x)}{\tau }+D_{\tau }^{1/2}{u}_k^h(x)+A_h^x{u}_k^h(x)=f_k^h(x),x\in {\overline{\mathrm{\Omega }}}_h,\\ f_k^h(x)=f^h(t_k,x),t_k=k\tau ,1\le k\le N,N\tau =T,\\ u_0^h(x)=0,x\in {\overline{\mathrm{\Omega }}}_h\end{array}$$

(3.2)

for the approximate solution of problem (1.8).

Moreover, applying the second order of approximation formula defined by (1.6) for

$$D_t^{1/2}u(t_k-\tau /2)=\frac{1}{\mathrm{\Gamma }(1/2)}{\int }_0^{t_k-\tau /2}{(t_k-\tau /2-s)}^{-1/2}{u}^{\mathrm{\prime }}(s)ds$$

and using the Crank-Nicholson difference scheme for parabolic equations, we can present the second order of accuracy difference scheme

$$\{\begin{array}{l}\frac{u_k^h(x)-u_{k-1}^h(x)}{\tau }+D_{\tau }^{1/2}{u}_k^h(x)+\frac{1}{2}{A}_h^x(u_k^h(x)+u_{k-1}^h(x))=f_k^h(x),x\in {\overline{\mathrm{\Omega }}}_h,\\ f_k^h(x)=f(t_k-\frac{\tau }{2},x),t_k=k\tau ,1\le k\le N,N\tau =T,\\ u_0^h(x)=0,x\in {\overline{\mathrm{\Omega }}}_h\end{array}$$

(3.3)

for the approximate solution of problem (1.8).

Theorem 3.1 Let τ and $|h|=\sqrt{h_1^2+\cdots +h_n^2}$ be sufficiently small numbers. Then the solutions of difference scheme (3.2) satisfy the following almost coercive stability estimates:

$$\begin{array}{r}\underset{1\le k\le N}{max}{\parallel \frac{u_k^h-u_{k-1}^h}{\tau }\parallel }_{C_h}\le M_{2}ln\frac{1}{\tau +|h|}\underset{1\le k\le N}{max}{\parallel f_k^h\parallel }_{C_h},\\ \underset{1\le k\le N}{max}\sum _{p=1}^m{\parallel {\left(u_k^h\right)}_{{\overline{x}}_p{x}_p,j_p}\parallel }_{C_h}\le M_2(\sigma )ln\frac{1}{h}ln\frac{1}{\tau +|h|}\underset{1\le k\le N}{max}{\parallel f_k^h\parallel }_{C_h}.\end{array}$$

The proof of Theorem 3.1 is based on the abstract Theorem 1.2 and on the estimate

$$min\{ln\frac{1}{\tau },1+|ln{\parallel A_h^x\parallel }_{C_h\to C_h}\left|\right\}\le M(\sigma )ln\frac{1}{\tau +|h|}$$

(3.4)

as well as on the positivity of the operator $A_h^x$ in $C_h$ [47, 48], along with the following theorem on the almost coercivity inequality for the solution of the elliptic difference equation in $C_h$.

Theorem 3.2 [49]

Let $|h|=\sqrt{h_1^2+\cdots +h_n^2}$ be sufficiently small number. Then, for the solutions of the elliptic difference equation

$$A_h^x{u}^h(x)={\omega }^h(x),x\in {\mathrm{\Omega }}_h$$

(3.5)

the following almost coercivity inequality

$$\sum _{p=1}^m{\parallel u_{{\overline{x}}_p{x}_p,j_p}^h\parallel }_{C_h}\le M(\sigma )ln\frac{1}{|h|}{\parallel {\omega }^h\parallel }_{C_h}$$

is valid.

Theorem 3.3 Let τ and $|h|=\sqrt{h_1^2+\cdots +h_m^2}$ be sufficiently small numbers. Then the solutions of difference scheme (3.3) satisfy the following almost coercive stability estimates:

$$\begin{array}{r}\underset{1\le k\le N}{max}{\parallel \frac{u_k^h-u_{k-1}^h}{\tau }\parallel }_{C_h}\le M_{3}ln\frac{1}{\tau +|h|}\underset{1\le k\le N}{max}{\parallel f_k^h\parallel }_{C_h},\\ \underset{1\le k\le N}{max}\frac{1}{2}\sum _{p=1}^m{\parallel {(u_k^h+u_{k-1}^h)}_{{\overline{x}}_p{x}_p,j_p}\parallel }_{C_h}\le M_3(\sigma )ln\frac{1}{h}ln\frac{1}{\tau +|h|}\underset{1\le k\le N}{max}{\parallel f_k^h\parallel }_{C_h}.\end{array}$$

The proof of Theorem 3.3 is based on the abstract Theorem 2.2 and on estimate (3.4) and on the positivity of the operator $A_h^x$ in $C_h$ and on Theorem 3.2 on the almost coercivity inequality for the solution of the elliptic difference equation in $C_h$.

Note that one has not been able to get a sharp estimate for the constants figuring in the almost coercive stability estimates of Theorems 3.1 and 3.3. Therefore, our interest in the present paper is studying the difference schemes (3.2) and (3.3) by numerical experiments. Applying these difference schemes, the numerical methods are proposed in the following section for solving the one-dimensional fractional parabolic partial differential equation. The method is illustrated by numerical experiments.

4 Numerical results

For the numerical result, the initial value problem

$$\{\begin{array}{l}\frac{\partial u(t,x)}{\partial t}+D_t^{1/2}u(t,x)-\frac{\partial }{\partial x}((1+x)\frac{\partial u(t,x)}{\partial x})+u(t,x)=f(t,x),\\ f(t,x)=[3+t+\frac{16\sqrt{t}}{5\sqrt{\pi }}+(1+x){\pi }^{2}t]t^{2}cos\pi x\\ \phantom{f(t,x)=}+\pi t^{3}sin\pi x,0<t<1,0<x<1,\\ u_x(t,0)=u_x(t,1)=0,0\le t\le 1,\\ u(0,x)=0,0\le x\le 1\end{array}$$

(4.1)

for the one-dimensional fractional parabolic partial differential equation is considered. The exact solution of problem (4.1) is $u(t,x)=t^{3}cos\pi x$.

4.1 First order of accuracy difference scheme

Applying difference scheme (3.2), we obtain

$$\{\begin{array}{l}\frac{u_n^k-u_n^{k-1}}{\tau }+\frac{1}{\sqrt{\pi }}{\sum }_{r=1}^k\frac{\mathrm{\Gamma }(k-r+1/2)}{(k-r)!}(\frac{u_n^r-u_n^{r-1}}{{\tau }^{1/2}})\\ -\frac{1}{h}[(1+x_{n+1})\frac{u_{n+1}^k-u_n^k}{h}-(1+x_n)\frac{u_n^k-u_{n-1}^k}{h}]+u_n^k={\phi }_n^k,\\ {\phi }_n^k=f(t_k,x_n),t_k=k\tau ,1\le k\le N,x_n=nh,1\le n\le M-1,\\ u_0^k=u_1^k,u_{M-1}^k=u_M^k,0\le k\le N,\\ u_n^0=0,0\le n\le M.\end{array}$$

It can be rewritten in the matrix form

$$\{\begin{array}{l}A{U}_{n+1}+B{U}_n+C{U}_{n-1}=D{\phi }_n,1\le n\le M-1,\\ U_0=U_1,U_{M-1}=U_M,\end{array}$$

where

$$\begin{array}{r}A={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ 0& a_n& 0& \cdots & 0& 0\\ 0& 0& a_n& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & a_n& 0\\ 0& 0& 0& \cdots & 0& a_n\end{array}\right]}_{(N+1)\times (N+1)},\\ B={\left[\begin{array}{cccccc}{b}_{11}& 0& 0& \cdots & 0& 0\\ b_{21}& b_{22}& 0& \cdots & 0& 0\\ b_{31}& b_{32}& b_{33}& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ b_{N1}& b_{N2}& b_{N3}& \cdots & b_{NN}& 0\\ b_{N+1,1}& b_{N+1,2}& b_{N+1,3}& \cdots & b_{N+1,N}& b_{N+1,N+1}\end{array}\right]}_{(N+1)\times (N+1)},\\ C={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ 0& c_n& 0& \cdots & 0& 0\\ 0& 0& c_n& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & c_n& 0\\ 0& 0& 0& \cdots & 0& c_n\end{array}\right]}_{(N+1)\times (N+1)},\\ D={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ 0& 1& 0& \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & 0& 1\end{array}\right]}_{(N+1)\times (N+1)},\\ {\phi }_n={\left[\begin{array}{c}{\phi }_n^0\\ {\phi }_n^1\\ {\phi }_n^2\\ ⋮\\ {\phi }_n^{N-1}\\ {\phi }_n^N\end{array}\right]}_{(N+1)\times 1},U_q={\left[\begin{array}{c}{u}_q^0\\ u_q^1\\ u_q^2\\ ⋮\\ u_q^{N-1}\\ u_q^N\end{array}\right]}_{(N+1)\times 1},q=n\pm 1,n,\\ a_n=-\frac{1+x_{n+1}}{h^2},c_n=-\frac{1+x_n}{h^2},b_{11}=1,b_{21}=-\frac{1}{\sqrt{\tau }}-\frac{1}{\tau },\\ b_{22}=\frac{1}{\sqrt{\tau }}+\frac{1}{\tau }+\frac{2+x_{n+1}+x_n}{h^2}+1,b_{31}=-\frac{\mathrm{\Gamma }(1+1/2)}{\sqrt{\pi \tau }},\\ b_{32}=\frac{\mathrm{\Gamma }(1+1/2)-\mathrm{\Gamma }(1/2)}{\sqrt{\pi \tau }}-\frac{1}{\tau },b_{33}=\frac{1}{\sqrt{\tau }}+\frac{1}{\tau }+\frac{2+x_{n+1}+x_n}{h^2}+1,\\ b_{ij}=\{\begin{array}{ll}-\frac{\mathrm{\Gamma }(i-2+1/2)}{\sqrt{\pi \tau }(i-2)!},& j=1,\\ \sqrt{\pi \tau }[\frac{\mathrm{\Gamma }(i-j+1/2)}{(i-j)!}-\frac{\mathrm{\Gamma }(i-j-1+1/2)}{(i-j-1)!}],& 2\le j\le i-2,\\ \sqrt{\pi \tau }[\mathrm{\Gamma }(1+1/2)-\mathrm{\Gamma }(1/2)]-\frac{1}{\tau },& j=i-1,\\ \frac{1}{\sqrt{\tau }}+\frac{1}{\tau }+\frac{2+x_{n+1}+x_n}{h^2}+1,& j=i,\\ 0,& i<j\le N+1\end{array}\end{array}$$

for $i=4,5,\dots ,N+1$ and

$${\phi }_n^k=[3+k\tau +\frac{16\sqrt{k\tau }}{5\sqrt{\pi }}+(1+nh){\pi }^{2}k\tau ]{(k\tau )}^{2}cos(\pi nh)+\pi {(k\tau )}^{3}sin(\pi nh).$$

So, we have the second order difference equation with respect to n matrix coefficients. This type system was developed by Samarskii and Nikolaev [50]. To solve this difference equation, we have applied a procedure for difference equation with respect to k matrix coefficients. Hence, we seek a solution of the matrix equation in the following form:

$$U_j={\alpha }_{j+1}{U}_{j+1}+{\beta }_{j+1},U_M={(I-{\alpha }_M)}^{-1}{\beta }_M,j=M-1,\dots ,2,1,$$

where ${\alpha }_j$ ($j=1,2,\dots ,M$) are $(N+1)\times (N+1)$ square matrices and ${\beta }_j$ ($j=1,2,\dots ,M$) are $(N+1)\times 1$ column matrices defined by

$$\begin{array}{r}{\alpha }_{j+1}=-{(B+C{\alpha }_j)}^{-1}A,\\ {\beta }_{j+1}={(B+C{\alpha }_j)}^{-1}(D{\phi }_j-C{\beta }_j),j=1,2,\dots ,M-1,\end{array}$$

where $j=1,2,\dots ,M-1$, ${\alpha }_1$ is the $(N+1)\times (N+1)$ identity matrix and ${\beta }_1$ is the $(N+1)\times 1$ zero matrix.

4.2 Second order of accuracy difference scheme

Applying the formulas

$$\begin{array}{r}{u}_x(t_k,0)=\frac{u_1^k-u_0^k}{h}-\frac{h}{2}{u}_{xx}(t_k,0)+o\left(h^2\right),0\le k\le N,\\ u_x(t_k,M)=\frac{3u_M^k-4u_{M-1}^k+u_{M-2}^k}{2h}+o\left(h^2\right),0\le k\le N,\\ u_t(t_k,0)=\frac{u_0^{k+1}-u_0^{k-1}}{2\tau }+o\left({\tau }^2\right),1\le k\le N-1,\\ u_t(t_N,0)=\frac{3u_0^N-4u_0^{N-1}+u_0^{N-2}}{2\tau }+o\left({\tau }^2\right),k=N\end{array}$$

and using difference scheme (3.3), we obtain the second order of accuracy difference scheme in t and in x

$$\{\begin{array}{l}\frac{u_n^k-u_n^{k-1}}{\tau }+D_{\tau }^{1/2}{u}_n^k-\frac{1}{2}[(1+x_n)\frac{u_{n+1}^k-2u_n^k+u_{n-1}^k}{h^2}+\frac{u_{n+1}^k-u_{n-1}^k}{2h}-u_n^k\\ +(1+x_n)\frac{u_{n+1}^{k-1}-2u_n^{k-1}+u_{n-1}^{k-1}}{h^2}+\frac{u_{n+1}^{k-1}-u_{n-1}^{k-1}}{2h}-u_n^{k-1}]={\phi }_n^k,\\ {\phi }_n^k=f(t_k-\tau /2,x_n),t_k=k\tau ,x_n=nh,1\le k\le N,1\le n\le M-1,\\ u_0^0=0,k=0,\\ -\frac{h}{4\tau }{u}_0^{k-1}+[\frac{1}{h}+\frac{h}{2}{D}_{\tau }^{1/2}+\frac{h}{2}]u_0^k+\frac{h}{4\tau }{u}_0^{k+1}=\frac{1}{h}{u}_1^k+\frac{h}{2}{\phi }_0^k,1\le k\le N-1,\\ \frac{h}{4\tau }{u}_0^{N-2}-\frac{h}{\tau }{u}_0^{N-1}+[\frac{1}{h}+\frac{3h}{4\tau }+\frac{h}{2}{D}_{\tau }^{1/2}+\frac{h}{2}]u_0^N=\frac{1}{h}{u}_1^N+\frac{h}{2}{\phi }_0^N,k=N,\\ 3u_M^k-4u_{M-1}^k+u_{M-2}^k=0,0\le k\le N,\\ u_n^0=0,0\le n\le M.\end{array}$$

Here, $D_{\tau }^{1/2}{u}_n^k$ is the fractional difference derivative defined by the formula (1.6). It can be rewritten in the matrix form

$$\{\begin{array}{l}A{U}_{n+1}+B{U}_n+C{U}_{n-1}=D{\phi }_n,1\le n\le M-1,\\ E{U}_0=F{U}_1+R{\phi }_0,3U_M-4U_{M-1}+U_{M-2}=0,\end{array}$$

(4.2)

where

$$\begin{array}{r}A={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ a_n& a_n& 0& \cdots & 0& 0\\ 0& a_n& a_n& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & a_n& 0\\ 0& 0& 0& \cdots & a_n& a_n\end{array}\right]}_{(N+1)\times (N+1)},\\ B={\left[\begin{array}{cccccc}{b}_{11}& 0& 0& \cdots & 0& 0\\ b_{21}& b_{22}& 0& \cdots & 0& 0\\ b_{31}& b_{32}& b_{33}& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ b_{N1}& b_{N2}& b_{N3}& \cdots & b_{NN}& 0\\ b_{N+1,1}& b_{N+1,2}& b_{N+1,3}& \cdots & b_{N+1,N}& b_{N+1,N+1}\end{array}\right]}_{(N+1)\times (N+1)},\\ C={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ c_n& c_n& 0& \cdots & 0& 0\\ 0& c_n& c_n& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & c_n& 0\\ 0& 0& 0& \cdots & c_n& c_n\end{array}\right]}_{(N+1)\times (N+1)},\\ D={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ 0& 1& 0& \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & 0& 1\end{array}\right]}_{(N+1)\times (N+1)},\\ {\phi }_n={\left[\begin{array}{c}{\phi }_n^0\\ {\phi }_n^1\\ {\phi }_n^2\\ ⋮\\ {\phi }_n^{N-1}\\ {\phi }_n^N\end{array}\right]}_{(N+1)\times 1},U_q={\left[\begin{array}{c}{u}_q^0\\ u_q^1\\ u_q^2\\ ⋮\\ u_q^{N-1}\\ u_q^N\end{array}\right]}_{(N+1)\times 1},q=n\pm 1,n,\\ a_n=-\frac{1}{2}(\frac{1+x_n}{h^2}+\frac{1}{2h}),c_n=-\frac{1}{2}(\frac{1+x_n}{h^2}-\frac{1}{2h}),d=\frac{2}{\sqrt{\pi \tau }},\\ \lambda (r)=\sqrt{r+1/2}-\sqrt{r-1/2},\mu (r)=-\frac{1}{3}[{(r+1/2)}^{3/2}-{(r-1/2)}^{3/2}],\\ b_{11}=1,b_{21}=-\frac{d\sqrt{2}}{3}-\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},b_{22}=\frac{d\sqrt{2}}{3}+\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},\\ b_{31}=\frac{d2\sqrt{6}}{5},b_{32}=\frac{d\sqrt{6}}{5}-\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},b_{33}=\frac{d\sqrt{6}}{5}+\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},\\ b_{41}=d[\lambda (1)+\mu (1)],b_{42}=d[-3\lambda (1)-2\mu (1)]-\frac{d}{6\sqrt{2}},\\ b_{43}=d[2\lambda (1)+\mu (1)]-4\frac{d}{6\sqrt{2}}-\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},b_{44}=5\frac{d}{6\sqrt{2}}+\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},\\ b_{51}=d[2\lambda (2)+\mu (2)],b_{52}=d[-5\lambda (2)-2\mu (2)+\lambda (1)+\mu (1)],\\ b_{53}=d[3\lambda (2)+\mu (2)-3\lambda (1)-2\mu (1)]-\frac{d}{6\sqrt{2}},\\ b_{54}=d[2\lambda (1)+\mu (1)]-4\frac{d}{6\sqrt{2}}-\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},b_{55}=5\frac{d}{6\sqrt{2}}+\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},\\ b_{i,j}=\{\begin{array}{ll}d[(i-3)\lambda (i-3)+\mu (i-3)],& j=1,\\ d[(5-2i)\lambda (i-3)-2\mu (i-3)+(i-4)\lambda (i-4)+\mu (i-4)],& j=2,\\ d[(i-j+1)\lambda (i-j)+\mu (i-j)+(2j-2i+1)\lambda (i-j-1)\\ -2\mu (i-j-1)+(i-j-2)\lambda (i-j-2)+\mu (i-j-2)],& 3\le j\le i-3,\\ d[3\lambda (2)+\mu (2)-3\lambda (1)-2\mu (1)]-\frac{d}{6\sqrt{2}},& j=i-2,\\ d[2\lambda (1)+\mu (1)]-4\frac{d}{6\sqrt{2}}-\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},& j=i-1,\\ 5\frac{d}{6\sqrt{2}}+\frac{1}{\tau }+\frac{1+x_n}{h^2}+\frac{1}{2},& j=i,\\ 0,& i<j\le N+1\end{array}\end{array}$$

for $i=6,7,\dots ,N+1$ and

$${\phi }_n^k=[3+k\tau +\frac{16\sqrt{k\tau }}{5\sqrt{\pi }}+(1+nh){\pi }^{2}k\tau ]{(k\tau )}^{2}cos(\pi nh)+\pi {(k\tau )}^{3}sin(\pi nh).$$

For the solution of the matrix equation (4.2), we use the same algorithm as in the first order of accuracy difference scheme, where

$$\begin{array}{r}{u}_M={[3I-4{\alpha }_M+{\alpha }_{M-1}{\alpha }_M]}^{-1}\ast [(4I-{\alpha }_{M-1}){\beta }_M-{\beta }_{M-1}],\\ {\alpha }_1=E^{-1}F,{\beta }_1=E^{-1}R{\phi }_0,\\ F={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ 0& 1/h& 0& \cdots & 0& 0\\ 0& 0& 1/h& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 1/h& 0\\ 0& 0& 0& \cdots & 0& 1/h\end{array}\right]}_{(N+1)\times (N+1)},\\ R={\left[\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ 0& 1& 0& \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& 0& 0& \cdots & 1& 0\\ 0& 0& 0& \cdots & 0& 1\end{array}\right]}_{(N+1)\times (N+1)},\\ E={\left[\begin{array}{cccccc}{e}_{11}& 0& 0& \cdots & 0& 0\\ e_{21}& e_{22}& 0& \cdots & 0& 0\\ e_{31}& e_{32}& e_{33}& \cdots & 0& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ e_{N1}& e_{N2}& e_{N3}& \cdots & e_{NN}& 0\\ e_{N+1,1}& e_{N+1,2}& e_{N+1,3}& \cdots & e_{N+1,N}& e_{N+1,N+1}\end{array}\right]}_{(N+1)\times (N+1)},\\ e_{11}=1,e_{21}=-\frac{h}{4\tau }-\frac{4h}{3\sqrt{\pi \tau }},e_{22}=\frac{1}{h}+\frac{h}{2}+\frac{4h}{3\sqrt{\pi \tau }},e_{23}=\frac{h}{4\tau },\\ e_{31}=\frac{2\sqrt{2}h}{15\sqrt{\pi \tau }},e_{32}=\frac{-16\sqrt{2}h}{15\sqrt{\pi \tau }}-\frac{h}{4\tau },e_{33}=\frac{1}{h}+\frac{h}{2}+\frac{14\sqrt{2}h}{15\sqrt{\pi \tau }},e_{34}=\frac{h}{4\tau },\\ e_{41}=\frac{dh}{2}[(1+1/2)\lambda (1)+\mu (1)],e_{42}=\frac{dh}{2}[-4\lambda (1)-2\mu (1)+1/2\lambda (0)+\mu (0)],\\ e_{43}=-\frac{h}{4\tau }+\frac{dh}{2}[(2+1/2)\lambda (1)+\mu (1)-2-2(-1/3)],\\ e_{44}=\frac{1}{h}+\frac{h}{2}+\frac{dh}{2}[(1+1/2)\lambda (0)+\mu (0)],e_{45}=\frac{h}{4\tau },\\ e_{51}=\frac{dh}{2}[(2+1/2)\lambda (2)+\mu (2)],\\ e_{52}=\frac{dh}{2}[-2\cdot 3\lambda (2)-2\mu (2)+(1+1/2)\lambda (1)+\mu (1)],\\ e_{53}=\frac{dh}{2}[(2+1+1/2)\lambda (2)+\mu (2)-2\cdot 2\lambda (1)-2\mu (1)+1/2\lambda (0)+\mu (0)],\\ e_{54}=-\frac{h}{4\tau }+\frac{dh}{2}[(1+1+1/2)\lambda (1)+\mu (1)-2\lambda (0)-2\mu (0)],\\ e_{55}=\frac{1}{h}+\frac{h}{2}+\frac{dh}{2}[(1+1/2)\lambda (0)+\mu (0)],e_{56}=\frac{h}{4\tau },\\ e_{ij}=\{\begin{array}{ll}\frac{dh}{2}[(i-3+1/2)\lambda (i-3)+\mu (i-3)],& j=1,\\ \frac{dh}{2}[-2(i-2)\lambda (i-3)-2\mu (i-3)\\ +(i-4+1/2)\lambda (i-4)+\mu (i-4)],& j=2,\\ \frac{dh}{2}[(i-j+1+1/2)\lambda (i-j)+\mu (i-j)-2(i-j)\lambda (i-j-1)\\ -2\mu (i-j-1)+(i-j-2+1/2)\lambda (i-j-2)+\mu (i-j-2)],& 3\le j\le i-2,\\ -\frac{h}{4\tau }+\frac{dh}{2}[(2+1/2)\lambda (1)+\mu (1)-2\lambda (0)-2\mu (0)],& j=i-1,\\ \frac{1}{h}+\frac{h}{2}+\frac{dh}{2}[(1+1/2)\lambda (0)+\mu (0)],& j=i,\\ \frac{h}{4\tau },& j=i+1,\\ \frac{h}{4\tau }+\frac{dh}{2}[(i-N+2+1/2)\lambda (i-N+1)+\mu (i-N+1)\\ -2(i-N+1)\lambda (i-N)-2\mu (i-N)\\ +(i-N-1+1/2)\lambda (i-N-1)+\mu (i-N-1)],& j=N-1,\\ -\frac{h}{\tau }+\frac{dh}{2}[(2+1/2)\lambda (1)+\mu (1)-2\lambda (0)-2\mu (0)],& j=N,\\ \frac{1}{h}+\frac{h}{2}+\frac{3h}{4\tau }+\frac{dh}{2}[(1+1/2)\lambda (0)+\mu (0)],& j=N+1,\\ 0,& j>i+1\end{array}\end{array}$$

for $i=6,7,\dots ,N+1$ and

$${\phi }_0^k=(3+k\tau +\frac{16\sqrt{k\tau }}{5\sqrt{\pi }}+{\pi }^{2}k\tau ){(k\tau )}^2.$$

4.3 Error analysis

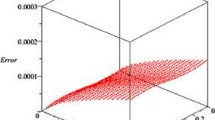
Finally, we give the results of the numerical analysis. The error is computed by the following formula

$$E_M^N=\underset{1\le k\le N,1\le n\le M-1}{max}|u(t_k,x_n)-u_n^k|,$$

where $u(t_k,x_n)$ represents the exact solution and $u_n^k$ represents the numerical solutions of these difference schemes at $(t_k,x_n)$.

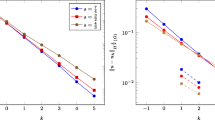
The numerical solutions are recorded for different values of N and M. Table 1 is constructed for $N=M=30,60\text{ and }120$, respectively.

Table 1 Comparison of errors

Thus, the results show that, by using the Crank-Nicholson difference scheme increases faster then the first order of accuracy difference scheme.

5 Conclusion

In the present study, the second order of accuracy difference scheme for the approximate solution of initial value problem (1.1) is presented. A theorem on almost coercivity of this difference scheme in maximum norm is established. Almost coercive stability estimates for the solution of the first and second order of accuracy stable difference schemes for the numerical solution of the initial boundary value problem for the fractional parabolic equation with the Neumann boundary condition are obtained. Of course, stability estimates permits us to obtain the convergence of difference schemes for the numerical solution of the initial boundary value problem for the fractional parabolic equation with the Neumann boundary condition. Moreover, the Banach fixed-point theorem and method of the present paper enables us to obtain the estimate of convergence of difference schemes of the first and second order of accuracy for approximate solutions of the initial-boundary value problem:

$$\{\begin{array}{l}\frac{\partial u(t,x)}{\partial t}+D_t^{\alpha }u(t,x)-{\sum }_{p=1}^m{a}_p(x)\frac{{\partial }^{2}u(t,x)}{\partial x_p^2}+\sigma u(t,x)\\ =f(t,x;u(t,x),u_{x_1}(t,x),\dots ,u_{x_m}(t,x)),x=(x_1,\dots ,x_m)\in \mathrm{\Omega },0<t<T,\\ \frac{\partial u(t,x)}{\partial \overrightarrow{n}}{|}_S=0,0\le t\le T,0\le \alpha <1,\\ u(0,x)=0,x\in \overline{\mathrm{\Omega }}\end{array}$$

for semilinear fractional parabolic partial differential equations with smooth $a_p(x)$ and $f(t,x;u(t,x),v_1(t,x),\dots ,v_m(t,x))$.