A mass conserved splitting method for the nonlinear Schrödinger equation

Abstract

A mass conserved time-splitting difference method is presented for the one-dimensional dipolar Bose-Einstein condensates (BECs) described by a nonlocal nonlinear Schrödinger equation with a convolution term. As a result of the singularity in the convolution term, it brings difficulties both in mathematical analysis and in numerical simulations. By properly using the difference scheme to deal with the convolution term, an imaginary time method is given to compute the ground states and then a time-splitting method is obtained for dynamics of dipolar BECs. This time-splitting numerical method is mass conserved everywhere, and it has second-order accuracy and is also unconditionally stable. Numerical results are given to verify the stability and energy conservation when there is no blow up.

Mathematics Subject Classification (2010) 65M06; 35Q41.

1 Introduction

Since its first experimental realization in dilute bosonic atomic gases in 1995, the Bose-Einstein condensation (BEC) of ultra-cold atomic and molecular gases has attracted considerable interests both theoretically and experimentally. Most of their properties of these trapped quantum gases are governed by the interactions between particles in the condensate [1]. In recent years, there has been an investigation for realizing a new kind of quantum gases with the dipolar interaction, acting between particles having a permanent magnetic or electric dipole moment. A BEC of ⁵²Cr atoms was realized [2, 3] at Stuttgart University in 2005, which paves the way towards the experimental as well as the theoretical and the numerical investigation on this novel dipolar quantum gases. The interest on dipolar gases has also been motivated by a broad range of exciting applications [4–6]. In such condensates, there are two kinds of interactions, namely, the short-range repulsive interaction between the particles as well as their long-range partially attractive/partially repulsive dipolar interactions. Therefore, the macroscopic condensate dynamics is determined by a dynamical equilibration of these forces [7, 8]. The effects of the interparticle interactions on the condensate properties have been widely discussed for the case of short-range interactions. However, since the dipole-dipole interactions are long range, anisotropic and partially attractive, the nontrivial task of achieving and controlling dipolar BECs is thus particularly challenging.

As we know, the properties of a BEC at temperatures T very much smaller than the critical temperature T_c are usually described by the nonlinear Schrödinger (NLS) equation for the macroscopic wave function known as the Gross-Pitaevskii (GP) equation. As far as the dipolar interaction is concerned, a convolution term is introduced [9–11] to modify the classical GP equation, which results in the following differential-integral equation

$$i\hslash {\psi }_t\left(\mathbf{x},t\right)=\left(-\frac{\hslash }{2m}{\nabla }^2+V\left(\mathbf{x}\right)+g{\left|\psi \left(\mathbf{x},t\right)\right|}^2+V_{\mathsf{\text{dip}}}\left(\mathbf{x}\right)*{\left|\psi \left(\mathbf{x},t\right)\right|}^2\right)\psi \left(\mathbf{x},t\right),$$

(1)

where ħ is the Planck constant, m the mass of the atom and V (x) is the external trapping potential, which is generally harmonic, and g = 4πħ²a _s /m is the local interactions between dipoles in the condensate with a_s the s wave scattering length (positive for repulsive interaction and negative for attractive interaction). V_dip(x) is the long-range isotropic dipolar interaction potential between two dipoles. The wave function ψ(x, t) is normalized according to

$${∥\psi ∥}^2=\underset{{ℝ}^3}{\int }{\left|\psi \left(\mathbf{x},t\right)\right|}^2\mathsf{\text{d}}\mathbf{x}=N,$$

(2)

where N is the number of the atoms in the dipolar BEC. The Equation 1 can be made dimensionless and simplified by adopting a unit system where the units for length, time and energy are given by a₀, 1/ω₀, and ħω₀, respectively, with ω₀ = min{ω₁, ω₂, ω₃}, $a_0=\sqrt{\frac{\hslash }{m{\omega }_0}}$. Here, we only consider the one-dimensional (1D) case. Apart from a conceptual clarity, lower dimensional dipolar BECs also offer a clear advantage for numerical computations. And also, in the case of radial symmetry in 2D and spherical symmetry in 3D (by tuning the trap frequencies), the multi-dimensional problem can be reduced to 1D case.

Now consider the following 1D dimensionless GP equation:

$$i\frac{\partial \psi \left(x,t\right)}{\partial t}=\left(-\frac{1}{2}{\nabla }^2+V\left(x\right)+\beta {\left|\psi \left(x,t\right)\right|}^2+\lambda V_{\mathsf{\text{dip}}}\left(x\right)*{\left|\psi \left(x,t\right)\right|}^2\right)\psi \left(x,t\right),$$

(3)

$$\psi \left(x,0\right)={\psi }_0\left(x\right),x\in ℝ,$$

(4)

where t is time, x is displacement, β and λ are two dimensionless real parameters stand for the strength of the short-range interaction between the particles and the long-range dipolar interaction, respectively. $\psi \left(x,t\right):ℝ\times {ℝ}^{+}\to ℂ$ is a complex-valued function, V (x) = x²/ 2 stands for the harmonic potential in 1D, V_dip(x) = |x|^-α, 0 < α < 1 is the convolution kernel representing the dipolar potential and * is the standard convolution in , i.e.,

$$V_{\text{dip}}(x)\ast |\psi (x,t){|}^2={\displaystyle \underset{ℝ}{\int }\frac{|\psi (y,t){|}^2}{|x-y{|}^{\alpha }}}\text{d}y,x,y\in ℝ.$$

(5)

In order to study the ground states and dynamics of dipolar BECs, an efficient numerical method is necessary. For the study in mathematics, the existence and uniqueness as well as the possible blowup of solutions were studied in [12], and the existence of standing waves was proven in [13, 14]. Due to the dipolar interaction potential of the nonlocal NLS, mathematical and numerical difficulties are introduced. Currently, the Fourier transform [15, 16] is generally used for dealing with the convolution in (3). However, there are two limitations in these numerical methods: (i) the Fourier transform of the dipolar interaction potential V_dip(x) and the density function is usually carried out in the whole space in the continuous level, while they are carried out on a bounded domain Ω in the discrete level, so there is a locking phenomena in practical computation as observed in [17]; (ii) the denominator of the dipolar interaction potential equals zero when x equals y, thus this singularity may cause some numerical difficulties too. The purpose here is to present a robust method for computing ground states and dynamics of dipolar BECs without these two limitations. The key issue is to deal with the convolution term in the nonlocal NLS equation efficiently.

This paper is organized as follows. In Sect. 2, some analytic results are given for the nonlocal NLS. In Sect. 3, a Crank-Nicolson numerical method is presented for computing ground states of dipolar BECs. In Sect. 4, a time-splitting numerical scheme is proposed for computing the dynamics. Numerical results are reported to verify the efficiency of this numerical method in Sect. 5. Finally, some concluding remarks are drawn in Sect. 6.

2 Analytical results

Two important invariants of (3) are the mass (or normalization) of the wave function

$$N(\psi (x,t)):={\Vert \psi (x,t)\Vert }^2={\displaystyle \underset{ℝ}{\int }|}\psi (x,t){|}^2\text{d}x\equiv {\displaystyle \underset{ℝ}{\int }|}\psi (x,0){|}^2\text{d}x=1,t\ge 0,$$

(6)

and the energy of per particle

$$\begin{array}{ll}\hfill E\left(\psi \left(x,t\right)\right):& =\underset{ℝ}{\int }\left\{\frac{1}{2}{\left|\nabla \psi \right|}^2+V\left(x\right){\left|\psi \right|}^2+\frac{\beta }{2}{\left|\psi \right|}^4+\frac{\lambda }{2}\left(V_{\mathsf{\text{dip}}}\left(x\right)*{\left|\psi \right|}^2\right){\left|\psi \right|}^2\right\}\mathsf{\text{d}}x\\ \equiv E\left(\psi \left(x,0\right)\right),t\ge 0.\end{array}$$

(7)

In order to obtain the ground states, we take the ansatz

$$\psi \left(x,t\right)={\mathsf{\text{e}}}^{-i\mu t}\varphi \left(x\right),x\in ℝ,t\ge 0,$$

(8)

where $\mu \in ℝ$ is the chemical potential and ϕ := ϕ(x) is a time-independent function. Inserting (8) into (3), we get the time-independent GP equation or the eigenvalue problem

$$\mu \varphi \left(x\right)=\left(-\frac{1}{2}{\nabla }^2+V\left(x\right)+\beta {\left|\varphi \left(x\right)\right|}^2+\lambda V_{\mathsf{\text{dip}}}\left(x\right)*{\left|\varphi \left(x\right)\right|}^2\right)\varphi \left(x\right),x\in ℝ,$$

(9)

under the constraint

$$\Vert \varphi \Vert :=\sqrt{{\displaystyle \underset{ℝ}{\int }|\varphi (x){|}^2\text{d}x}}=1.$$

(10)

The ground state of a dipolar BEC is defined as the solution of the following nonconvex minimization problem:

Find ϕ _g ∈ S and ${\mu }_g\in ℝ$ such that

$$E^g:=E\left({\varphi }_g\right)=\underset{\varphi \in S}{\text{min}}E\left(\varphi \right),{\mu }^g:=\mu \left({\varphi }_g\right),$$

(11)

where the nonconvex set S is defined as

$$S:=\left\{\varphi \left(x\right)|∥\varphi ∥=1,E\left(\varphi \right)<\infty \right\}.$$

(12)

And the chemical potential (or eigenvalue of (9)) is defined as

$$\begin{array}{ll}\hfill \mu \left(\varphi \right):& =\underset{ℝ}{\int }\left\{\frac{1}{2}|\nabla \varphi {|}^2+V\left(x\right)|\varphi {|}^2+\beta |\varphi {|}^4+\lambda \left(V_{\mathsf{\text{dip}}}\left(x\right)*|\varphi {|}^2\right)|\varphi {|}^2\right\}\mathsf{\text{d}}x\\ \equiv E\left(\varphi \right)+\frac{1}{2}\underset{ℝ}{\int }\left\{\beta |\varphi {|}^4+\lambda \left(V_{\mathsf{\text{dip}}}\left(x\right)*|\varphi {|}^2\right)|\varphi {|}^2\right\}\mathsf{\text{d}}x.\end{array}$$

(13)

The total energy in (7) is composed of kinetic, potential, interaction and dipolar energies, respectively, i.e.,

$$E\left(\varphi \right)=E_{\mathsf{\text{kin}}}\left(\varphi \right)+E_{\mathsf{\text{pot}}}\left(\varphi \right)+E_{\mathsf{\text{int}}}\left(\varphi \right)+E_{\mathsf{\text{dip}}}\left(\varphi \right),$$

(14)

where

$$\begin{array}{c}{E}_{\mathsf{\text{kin}}}\left(\varphi \right)=\frac{1}{2}\underset{ℝ}{\int }|\nabla \varphi {|}^2\mathsf{\text{d}}x,E_{\mathsf{\text{pot}}}\left(\varphi \right)=\underset{ℝ}{\int }V\left(x\right)|\varphi \left(x\right){|}^2\mathsf{\text{d}}x,\\ E_{\mathsf{\text{int}}}\left(\varphi \right)=\frac{\beta }{2}\underset{ℝ}{\int }|\varphi \left(x\right){|}^4\mathsf{\text{d}}x,E_{\mathsf{\text{dip}}}\left(\varphi \right)=\frac{\lambda }{2}\underset{ℝ}{\int }\left(V_{dip}\left(x\right)*|\varphi \left(x\right){|}^2\right)|\varphi {|}^2\mathsf{\text{d}}x,\end{array}$$

and ϕ(x) defined in (8) is a stationary state of a dipolar BEC.

3 Numerical method for computing ground states

In this section, we will propose an implicit numerical method for computing the ground states of a dipolar BEC. In practical computation, we usually truncate the problem (3) and (4) into a bounded computational domain Ω (chosen as an interval [−a, a] in 1D, with a sufficiently large), with homogeneous Dirichlet boundary condition. There are various numerical methods proposed in literatures for computing the ground states of BEC [8, 9, 16–19]. One of the efficient and popular techniques for the constraint (6) is through the following construction [13]: we choose a time step size τ > 0 and set t _k = k τ for k = 0, 1, . . .. Applying the imaginary time method [18] without considering the constraint (6), and then projecting the solution back to the unit nonconvex set S at the end of each time interval [t _k , t _{k +1}] to satisfy the constraint. Then the function ϕ(x, t) is the solution of the following gradient flow with discrete normalization [19]:

$$\frac{\partial \varphi \left(x,t\right)}{\partial t}=\left\{\frac{1}{2}{\nabla }^2-V\left(x\right)-\beta |\varphi \left(x,t\right){|}^2-\lambda V_{dip}\left(x\right)*|\varphi \left(x,t\right){|}^2\right\}\varphi \left(x,t\right),$$

(15)

$$\varphi \left(x,t\right){|}_{x\in \partial \Omega }=0,t\ge 0,$$

(16)

$$\varphi \left(x,t_{k+1}\right):=\varphi \left(x,t_{k+1}^{+}\right)=\frac{\varphi \left(x,t_{k+1}^{-}\right)}{∥\varphi \left(\cdot ,t_{k+1}^{-}\right)∥},x\in \Omega ,k\ge 1,$$

(17)

$$\varphi \left(x,0\right)={\varphi }_0\left(x\right),∥{\varphi }_0∥=1,$$

(18)

where $\varphi \left(x,t_k^{\pm }\right)=\underset{t\to t_k\pm }{\text{lim}}\varphi \left(x,t\right)$ and ϕ₀(x) is the initial condition.

Suppose M is a positive integer, choose the spatial step h = 2a/M, and define x _j = −a + j h, j = 0, 1, . . . , M. Let $F_j^k$ be the approximation of V_dip(x _j ) * |ϕ(x _j , t _k )|², and ${\varphi }_j^k$ be the approximations of (x _j , t _k ), which are the exact solution of (15)-(18) at the mesh grid (x _j , t _k ).

Choose ${\varphi }_j^0={\varphi }_0\left(x_j\right)$, j = 0, 1, . . . , M. From time t _k to t _{k +1}, a cental difference discretization for (15)-(18) is

$$\frac{{\varphi }_j^{k+1}-{\varphi }_j^k}{\tau }=\frac{1}{2h^2}{\delta }_x^2\left({\varphi }_j^{k+1/2}\right)-V\left(x_j\right){\varphi }_j^{k+1/2}-\beta \left(|{\varphi }_j^k{|}^2\right){\varphi }_j^{k+1/2}-\lambda F_j^k{\varphi }_j^{k+1/2},j=0,1,\dots ,M,$$

(19)

where

$$\begin{array}{ll}\hfill {\varphi }_j^{k+1/2}& =\left({\varphi }_j^{k+1}+{\varphi }_j^k\right)/2,{\delta }_x^2\left({\varphi }_j^k\right)={\varphi }_{j+1}^k-2{\varphi }_j^k+{\varphi }_{j-1}^k,\\ F_j^k=\sum _{r=0}^{M-1}\left(\frac{1}{1-\alpha }|\varphi \right.\left(x_r,t_k\right){|}^2\left|\right|\left(r+1-j\right)h{|}^{1-\alpha }-\left|\left(r-j\right)h{|}^{1-\alpha }\right|+\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-|\varphi \left(x_{r-1},t_k\right){|}^2}{2h}.\\ \left.\underset{0}{\overset{h}{\int }}\frac{s}{|\left(r-j\right)h+s{|}^{\alpha }}\mathsf{\text{d}}s+\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-2|\varphi \left(x_r,t_k\right){|}^2+|\varphi \left(x_{r-1},t_k\right){|}^2}{h^2}\cdot \underset{0}{\overset{h}{\int }}\frac{s^2}{2|\left(r-j\right)h+s{|}^{\alpha }}\mathsf{\text{d}}s\right),\end{array}$$

(20)

and the details of F _j ^k are given in the Appendix. Notice that in the above scheme, we replace $\beta \left(|{\varphi }_j^{k+1/2}{|}^2\right){\varphi }_j^{k+1/2}$, $F_j^{k+1/2}$ with $\beta \left(|{\varphi }_j^k{|}^2\right){\varphi }_j^{k+1/2}$ and F _j ^k , respectively, to linearize the nonlinear terms. It is easy to see that the local truncation error of (19) is O(h² + τ²) because 0 < α < 1. Using the classical finite difference method theory, we claim our numerical scheme is the second-order algorithm which will be justified by the numerical examples in Sect. 5.

4 Time-splitting numerical method for dynamics

We will propose a time-splitting finite difference (TSFD) method for computing the dynamics of a dipolar BEC based on the nonlocal NLS equation (3). The advantage of this method is to deal with the discretization of nonlinear terms in the NLS equation by solving an ordinary differential equation (ODE) exactly. By virtue of this way, the computational cost and complexity can be reduced. As in Sect. 3, the whole space problem is truncated into a bounded computational domain Ω = [−a, a] with homogeneous Dirichlet boundary condition.

From t = t _k to t = t _{k +1}, the GP equation (3)-(4) is solved by three steps. First, we solve

$$i\frac{\partial \psi \left(x,t\right)}{\partial t}=-\frac{1}{2}{\nabla }^2\psi \left(x,t\right),x\in \Omega ,$$

(21)

$$\psi \left(-a,t\right)=0,\psi \left(a,t\right)=0,$$

(22)

from t _k to t _{k +1/2}, followed by solving the nonlinear ODE

$$i\frac{\partial \psi \left(x,t\right)}{\partial t}=\left(V\left(x\right)+\beta |\psi \left(x,t\right){|}^2+\lambda V_{\mathsf{\text{dip}}}\left(x\right)*|\psi \left(x,t\right){|}^2\right)\psi \left(x,t\right),$$

(23)

$$\psi \left(-a,t\right)=0,\psi \left(a,t\right)=0,t_k\le t\le t_{k+1},$$

(24)

for one time step. Again, we slove (21) from t _{k +1/2} to t _{k +1}.

Equation 21 can be discretized in space by Crank-Nicolson scheme, and Equation 23 can be solved exactly. In fact, for t ∈ [t _k , t _{k +1}], multiplying (23) by the conjugation of ψ(x, t), i.e., $\overline{\psi \left(x,t\right)}$, we get

$$i\frac{\partial \psi \left(x,t\right)}{\partial t}\overline{\psi \left(x,t\right)}=\left(V\left(x\right)+\beta |\psi \left(x,t\right){|}^2+\lambda V_{\mathsf{\text{dip}}}\left(x\right)*|\psi \left(x,t\right){|}^2\right)\psi \left(x,t\right)\overline{\psi \left(x,t\right)},$$

(25)

and we also have

$$-i\frac{\partial \overline{\psi \left(x,t\right)}}{\partial t}\psi \left(x,t\right)=\left(V\left(x\right)+\beta |\psi \left(x,t\right){|}^2+\lambda V_{\mathsf{\text{dip}}}\left(x\right)*|\psi \left(x,t\right){|}^2\right)\overline{\psi \left(x,t\right)}\psi \left(x,t\right),$$

(26)

Therefore, subtracting (26) from (25), one obtains

$$i\frac{\mathsf{\text{d}}}{\mathsf{\text{d}}t}|\psi \left(x,t\right){|}^2=0.$$

which implies

$$|\psi \left(x,t\right){|}^2=|\psi \left(x,t_k\right){|}^2,t_k\le t\le t_{k+1}.$$

(27)

Substituting (27) into (23), we get a linear ODE

$$i\frac{\partial \psi \left(x,t\right)}{\partial t}=\left(V\left(x\right)+\beta |\psi \left(x,t_k\right){|}^2+\lambda V_{\mathsf{\text{dip}}}\left(x\right)*|\psi \left(x,t_k\right){|}^2\right)\psi \left(x,t\right)$$

(28)

which can be solved exactly. Integrating (28) from t _k to t , one gets

$$\psi \left(x,t\right)=\text{exp}\left\{-i\left[V\left(x\right)+\beta |\psi \left(x,t_k\right){|}^2+\lambda V_{dip}\left(x\right)*|\psi \left(x,t_k\right){|}^2\right]\left(t-t_k\right)\right\}\psi \left(x,t_k\right),t_k\le t\le t_{k+1}.$$

(29)

Let ψ _j ^k be the approximation of ψ(x _j , t _k ). Then a second-order TSFD method for solving (3)-(4) via the standard Strang splitting [20–22] is as follows:

$$\left\{\begin{array}{c}\hfill {\psi }_{j-1}^{\left(1\right)}+\left(4i/{\lambda }_0-2\right){\psi }_j^{\left(1\right)}+{\psi }_{j+1}^{\left(1\right)}=-{\psi }_{j-1}^k+\left(4i/{\lambda }_0+2\right){\psi }_j^k-{\psi }_{j+1}^k,\hfill \\ \hfill {\psi }_j^{\left(2\right)}=\text{exp}\left\{-i\tau \left[V\left(x_j\right)+\beta |{\psi }_j^{\left(1\right)}{|}^2+\lambda F_j^{\left(1\right)}\right]\right\}{\psi }_j^{\left(1\right)},j=1,2,\dots ,M-1,\hfill \\ \hfill {\psi }_{j-1}^{k+1}+\left(4i/{\lambda }_0-2\right){\psi }_j^{k+1}+{\psi }_{j+1}^{k+1}=-{\psi }_{j-1}^{\left(2\right)}+\left(4i/{\lambda }_0+2\right){\psi }_j^{\left(2\right)}-{\psi }_{j+1}^{\left(2\right)},\hfill \end{array}\right.$$

(30)

where λ₀ = τ/2h², ψ _M = 0 and $F_j^{\left(1\right)}=V_{\mathsf{\text{dip}}}\left(x_j\right)*|{\psi }_j^{\left(1\right)}{|}^2$.

The above method is implicit, unconditionally stable. In fact, for the stability or conservation, we have

Theorem 1. The scheme (30) is normalization conservation, i.e.,

$${∥{\psi }^{k+1}∥}_{l^2}^2:=h\sum _{j=0}^M|{\psi }_j^{k+1}{|}^2\equiv h\sum _{j=0}^M|{\psi }_j^0{|}^2={∥{\psi }^0∥}_{l^2}^2,k\ge 0.$$

(31)

Proof. According to the first equation of (30), if we denote $A_j={\psi }_j^{\left(1\right)}+{\psi }_j^k$, we have

$$\frac{4i}{{\lambda }_0}\left({\psi }_j^{\left(1\right)}-{\psi }_j^k\right)=-\left(A_{j-1}+A_{j+1}\right)+2A_j.$$

(32)

Multiplying (32) by the conjugation of A _j , one gets

$$\frac{4i}{{\lambda }_0}\left(|{\psi }_j^{\left(1\right)}{|}^2+{\psi }_j^{\left(1\right)}{\psi }_j^{k*}-{\psi }_j^{\left(1\right)*}{\psi }_j^k-|{\psi }_j^k{|}^2\right)=-\left(A_{j-1}+A_{j+1}\right)A_j^{*}+2|A_j{|}^2.$$

(33)

Therefore

$$-\frac{4i}{{\lambda }_0}\left(|{\psi }_j^{\left(1\right)}{|}^2+{\psi }_j^{\left(1\right)*}{\psi }_j^k-{\psi }_j^{\left(1\right)}{\psi }_j^{k*}-|{\psi }_j^k{|}^2\right)=-\left(A_{j-1}^{*}+A_{j+1}^{*}\right)A_j+2|A_j{|}^2.$$

Combine the above two equations, we have

$$\frac{8i}{{\lambda }_0}\left(|{\psi }_j^{\left(1\right)}{|}^2-|{\psi }_j^k{|}^2\right)=-\left(A_{j-1}+A_{j+1}\right)A_j^{*}+\left(A_{j-1}^{*}+A_{j+1}^{*}\right)A_j$$

(34)

Then let j be 1, 2, . . . , M − 1, respectively, in (34) and add them together, it is easy to see that, the right-hand side vanishes due to the homogeneous Dirichlet boundary condition ψ₀ = ψ _M = 0.

Therefore, we have the following equation

$$\sum _{j=1}^{M-1}|{\psi }_j^{\left(1\right)}{|}^2=\sum _{j=1}^{M-1}|{\psi }_j^k{|}^2.$$

(35)

Similarly, the following equation is obtained from the third equation of (30),

$$\sum _{j=1}^{M-1}|{\psi }_j^{k+1}{|}^2=\sum _{j=1}^{M-1}|{\psi }_j^{\left(2\right)}{|}^2.$$

(36)

Based on Equation (29) and the second equation of (30), we have

$$\sum _{j=1}^{M-1}|{\psi }_j^{\left(2\right)}{|}^2=\sum _{j=1}^{M-1}{\left|\text{exp}\left\{-i\tau \left[V\left(x_j\right)+|{\psi }_j^{\left(1\right)}{|}^2+\lambda F_j^{\left(1\right)}\right]\right\}{\psi }_j^{\left(1\right)}\right|}^2=\sum _{j=1}^{M-1}|{\psi }_j^{\left(1\right)}{|}^2.$$

(37)

Combining (35), (36) with (37), we have

$$\sum _{j=1}^{M-1}|{\psi }_j^{k+1}{|}^2=\sum _{j=1}^{M-1}|{\psi }_j^k{|}^2.$$

Owing to the boundary condition, we have ${∥{\psi }^{k+1}∥}_{l^2}^2={∥{\psi }^k∥}_{l^2}^2$, which implies the l² stable property, i.e., ${∥{\psi }^{k+1}∥}_{l^2}\equiv {∥{\psi }^0∥}_{l^2},k\ge 0$.

5 Numerical results

In this section, we first evaluate numerically the convolution term and then report ground states and dynamics of dipolar BECs using our numerical method.

5.1 Error for the convolution term

To test the accuracy of this numerical method, correct computation of the convolution term is important. We take ϕ(x) = x^{3/ 2}for example, as the convolution term V_dip *|ϕ(x)|² can be computed exactly in this case. Based on our numerical method, i.e., (20), the numerical result shows at least the second-order accuracy. And in fact, it is almost the third-order accuracy. We choose α = 0.5 and solve this problem on [0, 10]. Table 1 shows the maximum errors with different sizes h.

Table 1 Comparison for evaluating the convolution term under varying spatial sizes h

From Table 1, one can see that our new method has a higher order accuracy between the second-order and the third-order in space for evaluating the convolution term.

5.2 Ground states of dipolar BECs

Using numerical scheme (15)-(18), the ground states of a dipolar BEC with different parameters are given. The initial condition is ${\varphi }_0\left(x\right)=\frac{1}{{\pi }^{1/4}}{e}^{-x^2/2}$. We solve this problem on [− 16, 16] with h = 1/ 8 and τ = 0.001. ϕ _g := ϕ^k+1 is reached numerically when

$${∥{\varphi }^{k+1}-{\varphi }^k∥}_{\infty }:=\underset{0\le j\le M}{\text{max}}|{\varphi }_j^{k+1}-{\varphi }_j^k|\le \epsilon :=10^{-6}$$

in (15). Figure 1 shows the plot of the ground state ϕ _g (x), of a dipolar BEC with λ = − 0.2 and β = 0.5. Table 2 shows the energy E^g , chemical potential µ^g , kinetic energy $E_{\mathsf{\text{kin}}}^g:=E_{\mathsf{\text{kin}}}\left({\varphi }_g\right)$, potential energy $E_{\mathsf{\text{pot}}}^g:=E_{\mathsf{\text{pot}}}\left({\varphi }_g\right)$, interaction energy $E_{\mathsf{\text{int}}}^g:=E_{\mathsf{\text{int}}}\left({\varphi }_g\right)$, dipolar energy $E_{\mathsf{\text{dip}}}^g:=E_{\mathsf{\text{dip}}}\left({\varphi }_g\right)$, and the maximum value of the wave function ϕ _g (0) with α = 0.5 and potential V (x) = x²/ 2 for different λ and β with fixed λ/β = − 0.4; Table 3 gives computational results with β = 0.5 for different values of − 0.5 ≤ λ/β ≤ 1. In addition, since the GP equation has no analytical solution, we take the numerical solution in a finer mesh with M = 2048 and τ = 0.001 as the "exact" solution, and the maximum error are given in Table 4.

Figure 1

The ground state of a dipolar BEC with λ = − 0.2 and β = 0.5.

Table 2 The ground states of a dipolar BEC for different λ and β with fixed values of λ/β = − 0.4.

Table 3 The ground states of a dipolar BEC with different values of λ/β for β = 0.5

Table 4 The maximum error of the ground state with different mesh

From Tables 2, 3, 4, and Figure 1, we make the following conclusions: when λ increases or β decreases with fixed λ/β = − 0.4, the maximum value of the wave function ϕ _g (0), kinetic energy $E_{\mathsf{\text{kin}}}^g$, dipolar energy $E_{\mathsf{\text{dip}}}^g$, energy E^g as well as the chemical potential µ^g increase; the potential energy $E_{\mathsf{\text{pot}}}^g$, interaction energy $E_{\mathsf{\text{int}}}^g$, and the radius mean square $x_{\mathsf{\text{rms}}}^g$, defined by $x_{\mathsf{\text{rms}}}=\sqrt{\underset{ℝ}{\int }{x}^2|{\varphi }_g\left(x\right){|}^2\mathsf{\text{d}}x}$ decrease (cf. Table 2). For fixed β , when the ratio λ/β increases from − 0.5 to 1, $E_{\mathsf{\text{pot}}}^g$,$E_{\mathsf{\text{dip}}}^g$, E^g µ^g , and x_rms of the ground states increase; the maximum value of the wave function ϕ _g (0), $E_{\mathsf{\text{kin}}}^g$, and $E_{\mathsf{\text{int}}}^g$ decrease (cf. Table 3). This numerical method is second-order accurate and can compute the ground states efficiently (cf. Figure 1; Table 4).

5.3 Dynamics of dipolar BECs

By applying our numerical method (30), the dynamics of a dipolar BEC is considered. We apply the bounded computational domain [− 8, 8], M = 128, i.e., h = 1/ 8, time step τ = 0.01. The initial data is chosen the same as in the case of computing the ground state of a dipolar BEC.

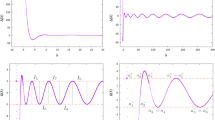
Figure 2 depicts the evolution of kinetic energy E_kin(t):= E_kin(ψ(·, t)), potential energy E_pot(t):= E_pot(ψ(·, t)), interaction energy E_int(t):= E_int(ψ(·, t)), dipolar energy E_dip(t):= E_dip(ψ(·, t)), the energy E(t):= E(ψ(·, t)) as well as the chemical potential µ(t) := µ(ψ(·, t)), condensate width ${\sigma }_x:={\sigma }_x(\psi (·,t))={\displaystyle \underset{ℝ}{\int }{x}^2}|\psi (x,t){|}^2\text{d}x$, and l₂ norm ${∥\psi \left(\cdot ,t\right)∥}_{l^2}$ for the case of β = 5.0 and λ = − 0.8. In addition, Figure 3 shows the results for the case of β = 25 and λ = 0.8. Figure 4 shows the results for the case of β = − 25 and λ = 80.

Figure 2

Time evolution at different times for a dipolar BEC with β = 5.0 and λ = − 0.8.

Figure 3

Time evolution at different times for a dipolar BEC with β = 25.0 and λ = 0.8.

Figure 4

Time evolution for a dipolar BEC with β = − 25.0 and λ = 80.0.

From Figures 2, 3, and 4, we can obtain the conclusion that global existence of the solution is observed in the first two cases (cf. Figures 2, 3) and finite time blow-up is observed in the last case (cf. Figure 4). The total energy is numerically conserved in our computation when there is no blow-up (cf. Figures 2, 3) and the discrete l²-norm ||ψ|| is numerically conserved very well whether there is blow-up or not (cf. Figures 2, 3, 4).

6 Conclusions

Efficient numerical methods are presented for computing ground states and dynamics of dipolar Bose-Einstein condensates based on the one-dimensional Grosss-Pitaevskii equation with a nonlocal dipolar interaction potential. By applying the difference method, the discretization of the dipolar interaction potential term is given. The imaginary method and time-splitting difference method are given for computing the ground states and dynamics of a dipolar BEC, respectively. Our numerical method is mass conserved and second-order accurate. In addition, the proof of the discrete energy conservation is an open problem. We only find the energy conservation from a numerical point of view. Numerical results are given to demonstrate the efficiency of our numerical method.

Appendix

The discretization of the convolution term

Here, we need to handle the convolution term

$$V_{\mathsf{\text{dip}}}\left(x\right)*|\psi \left(x,t\right){|}^2=|x{|}^{-\alpha }*|\psi {|}^2=\underset{R}{\int }\frac{1}{|x-y{|}^{\alpha }}|\psi \left(y,t\right){|}^2\mathsf{\text{d}}y$$

First, consider $|x{|}^{-\alpha }*|\psi {|}^2{|}_{\left(x_j,t_k\right)}$, i.e., ${\int }_{x_0}^{x_M}\frac{|\psi {\left(y,t_k\right)}^2}{|x_j-y{|}^{\alpha }}\mathsf{\text{d}}y$ where [x₀, x _M ] is the discretizised integration area. It is easy to see that x _j is a singular point and we need to deal with it piecewisely. We denote $I={\int }_{x_0}^{x_M}\frac{|\psi {\left(y,t_k\right)}^2}{|x_j-y{|}^{\alpha }}\mathsf{\text{d}}y$, let the convolution term be two parts, we have

$$\underset{x_0}{\overset{x_M}{\int }}\frac{|\varphi \left(y,t_k\right){|}^2}{|x_j-y{|}^{\alpha }}\mathsf{\text{d}}y=I_1+I_2,$$

(A.1)

where

$$I_1=\underset{x_0}{\overset{x_j}{\int }}\frac{|\varphi \left(y,t_k\right){|}^2}{|x_j-y{|}^{\alpha }}\mathsf{\text{d}}y,I_2=\underset{x_j}{\overset{x_M}{\int }}\frac{|\varphi \left(y,t_k\right){|}^2}{|x_j-y{|}^{\alpha }}\mathsf{\text{d}}y.$$

(A.2)

For I₁ in (A.2), let y = x _r + s, we have

$$I_1=\sum _{r=0}^{j-1}\underset{x_r}{\overset{x_{r+1}}{\int }}\frac{|\varphi \left(y,t_k\right){|}^2}{{\left(x_j-y\right)}^{\alpha }}\mathsf{\text{d}}y=\sum _{r=0}^{j-1}\underset{0}{\overset{h}{\int }}\frac{|\varphi \left(x_r+s,t_k\right){|}^2}{{\left(x_j-x_r-s\right)}^{\alpha }}\mathsf{\text{d}}s.$$

Then, substituting |ϕ(x _r + s, t _k )|² by the Taylor expansion at (x _r , t _k ), we obtain

$$\begin{array}{ll}\hfill I_1& =\sum _{r=0}^{j-1}\underset{0}{\overset{h}{\int }}\frac{1}{{\left(x_j-x_r-s\right)}^{\alpha }}\left[|{\left.\varphi \left(x_r,t_k\right){|}^2+\frac{\partial \left(|\varphi \left(s,t_k\right){|}^2\right)}{\partial s}\right|}_{s=x_r}{\left.s+\frac{{\partial }^2\left(|\varphi \left(s,t_k\right){|}^2\right)}{\partial s^2}\right|}_{s=x_r}\frac{1}{2}{s}^2+O\left(s^3\right)\right]\mathsf{\text{d}}s\\ =\sum _{r=0}^{j-1}\left[{\left.\frac{-1}{1-\alpha }|\varphi \left(x_r,t_k\right){|}^2{\left(x_j-x_r-s\right)}^{1-\alpha }\right|}_0^h{\left.+\frac{\partial \left(|\varphi \left(s,t_k\right){|}^2\right)}{\partial s}\right|}_{s=x}\underset{r_0}{\overset{h}{\int }}\frac{s}{{\left(x_j-x_r-s\right)}^{\alpha }}\mathsf{\text{d}}s\right.\\ \left.{\left.+\frac{{\partial }^2\left(|\varphi \left(s,t_k\right){|}^2\right)}{\partial s^2}\right|}_{s=x_r}\underset{0}{\overset{h}{\int }}\frac{s^2}{2{\left(x_j-x_r-s\right)}^{\alpha }}\mathsf{\text{d}}s+O\left(h^{4-\alpha }\right)\right]\\ =\sum _{r=0}^{j-1}\left(\frac{1}{1-\alpha }\right.|\varphi \left(x_r,t_k\right){|}^2\left\{{\left[\left(j-r\right)h\right]}^{1-\alpha }-{\left[\left(j-r-1\right)h\right]}^{1-\alpha }\right\}\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-|\varphi \left(x_{r-1},t_k\right){|}^2}{2h}+O\left(h^2\right)\right]\underset{0}{\overset{h}{\int }}\frac{s}{{\left(x_j-x_r-s\right)}^{\alpha }}\mathsf{\text{d}}s\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-2|\varphi \left(x_r,t_k\right){|}^2+|\varphi \left(x_{r-1},t_k\right){|}^2}{h^2}+O\left(h^2\right)\right]\left.\underset{0}{\overset{h}{\int }}\frac{s^2}{2{\left(x_j-x_r-s\right)}^{\alpha }}\mathsf{\text{d}}s+O\left(h^{4-\alpha }\right)\right)\\ =\sum _{r=0}^{j-1}\left(\frac{1}{1-\alpha }|\varphi \right.\left(x_r,t_k\right){|}^2\left\{{\left[\left(j-r\right)h\right]}^{1-\alpha }-{\left[\left(j-r-1\right)h\right]}^{1-\alpha }\right\}\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-|\varphi \left(x_{r-1},t_k\right){|}^2}{2h}\right]\underset{0}{\overset{h}{\int }}\frac{s}{{\left[\left(j-r\right)h-s\right]}^{\alpha }}\mathsf{\text{d}}s\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-2|\varphi \left(x_r,t_k\right){|}^2+|\varphi \left(x_{r-1},t_k\right){|}^2}{h^2}\right]\left.\underset{0}{\overset{h}{\int }}\frac{s^2}{2{\left[\left(j-r\right)h-s\right]}^{\alpha }}\mathsf{\text{d}}s\right)+O\left(h^{3-\alpha }\right).\end{array}$$

(A.3)

Similarly, for I₂ in (A.2), we get

$$\begin{array}{ll}\hfill I_2& =\sum _{r=j}^{M-1}\left(\frac{1}{1-\alpha }|\varphi \right.\left(x_r,t_k\right){|}^2\left\{{\left[\left(r+1-j\right)h\right]}^{1-\alpha }-{\left[\left(r-j\right)h\right]}^{1-\alpha }\right\}\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-|\varphi \left(x_{r-1},t_k\right){|}^2}{2h}\right]\underset{0}{\overset{h}{\int }}\frac{s}{{\left[\left(r-j\right)h+s\right]}^{\alpha }}\mathsf{\text{d}}s\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-2|\varphi \left(x_r,t_k\right){|}^2+|\varphi \left(x_{r-1},t_k\right){|}^2}{h^2}\right]\left.\underset{0}{\overset{h}{\int }}\frac{s^2}{2{\left[\left(r-j\right)h+s\right]}^{\alpha }}\mathsf{\text{d}}s\right)+O\left(h^{3-\alpha }\right).\end{array}$$

(A.4)

Combining (A.1), (A.3) and (A.4), we obtain the discretization of convolution term

$$\begin{array}{ll}\hfill F_j^k& =\sum _{r=0}^{M-1}\left(\frac{1}{1-\alpha }\right.\left|\varphi \left(x_r,t_k\right){|}^2\right||\left(r+1-j\right)h{|}^{1-\alpha }-|\left(r-j\right)h{|}^{1-\alpha }|\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-|\varphi \left(x_{r-1},t_k\right){|}^2}{2h}\right]\underset{0}{\overset{h}{\int }}\frac{s}{|\left(r-j\right)h+s{|}^{\alpha }}\mathsf{\text{d}}s\\ +\left[\frac{|\varphi \left(x_{r+1},t_k\right){|}^2-2|\varphi \left(x_r,t_k\right){|}^2+|\varphi \left(x_{r-1},t_k\right){|}^2}{h^2}\right]\left.\underset{0}{\overset{h}{\int }}\frac{s^2}{2|\left(r-j\right)h+s{|}^{\alpha }}\mathsf{\text{d}}s\right).\end{array}$$

(A.5)

with the local truncation error O(h^3-α). Moreover, The integrals in (A.3), (A.4) and (A.5) can be calculated analytically, we omit here for brevity.