Isochronal function projective synchronization between chaotic and time-delayed chaotic systems

Abstract

Isochronal function projective synchronization between chaotic and time-delayed chaotic systems with unknown parameters is investigated in this article. Based on Lyapunov stability theory, adaptive controllers and parameter updating laws are designed to achieve the isochronal function projective synchronization between chaotic and time-delayed chaotic systems. The scheme is applied to realize the synchronization between time-delayed Lorenz systems and time-delayed hyper-chaotic Chen systems, respectively. Numerical simulations are also presented to show the effectiveness of the proposed method.

Mathematics Subject Classification 2000: 34C28; 34D20; 37N35.

1. Introduction

In the last few years, chaos synchronization has gained a lot of attention for its potential applications in some engineering applications, such as image processing, chemical and biological systems, information science and in particular secure communication. Since the pioneering work of Pecora and Carroll [1], in which complete synchronization between two identical chaotic systems with different initial conditions was realized, various approaches have been put forward for synchronization of chaotic systems, such as complete synchronization [2], phase synchronization [3], generalized synchronization [4], lag synchronization [5], projective synchronization [6], modified projective synchronization [7, 8] and function projective synchronization [9–11], function projective lag synchronization [12], anti-synchronization [13] and so on.

Among all types of chaos synchronization, projective synchronization phenomenon is of great significance for its potential application in secure communication. In 1999, Mainieri and Rehacek [14] first proposed the concept of projective synchronization, which is characterized that the drive and the response systems could be synchronized up to a scaling factor. Because of the proportionality between its synchronized dynamical states, the feature can be used to M-nary digital communication for achieving fast communication. So projective synchronization have attracted increasing attention during recent years and some conditions ensuring projective synchronization have been obtained. Recently, some scholars extended the concept of projective synchronization and proposed modified projective synchronization [15], function projective synchronization [16] and modified function projective synchronization [17, 18], in which master and slave system are synchronized with a scaling function matrix.

As we know, delayed differential equations could exhibit complex dynamical behaviors and have attracted much attention in the field of nonlinear dynamics. Note that research on synchronization between time-delayed chaotic systems has been extensively carried out, see, for example, [19–21]. Recently, dual-anticipating, dual and dual-lag synchronization [22] between two identical time-delayed chaotic systems, lag synchronization [23] were investigated, where lag or anticipatory dynamics occurred, i.e., there existed a lag time or anticipatory time phase shift between state vectors. While results about zero lag time difference between synchronized state shifts, i.e., isochronal synchronization [24, 25] are also obtained between time-delayed systems. Note that projective synchronization [26, 27] between time-delayed chaotic systems was extensively investigated. However, results about isochronal function projective synchronization between chaotic and time-delayed chaotic systems are still few. In this article, isochronal function projective synchronization scheme between chaotic and time-delayed chaotic systems with unknown parameters is proposed. The method is shown to be effective by applying to Lorenz and hyper-chaotic Chen systems.

The remainder of this article is organized as follows. In Section 2 the synchronization scheme is presented. Section 3 is devoted to the application of the proposed scheme to Lorenz and hyper-Chaotic systems, respectively. Numerical simulations are also presented to demonstrate the effectiveness of the method. Some conclusions are drawn in Section 4.

2. Statement of the problem

Consider the chaotic system given by

$$\dot{x}=F(x)\theta +G(x)\beta +f(x),$$

(1)

where x ∈ Rⁿdenotes the state vector, F, G : Rⁿ→ R^{n × p}are continuous function matrices, f : Rⁿ→ Rⁿis a continuous nonlinear vector function, θ, β ∈ R^pare parameter vectors. Note that many chaotic and hyper-chaotic systems, such as Lorenz system, Chen system, Lü system, Rössler system, hyper-chaotic Chen system, etc, could be described by system (1).

The time-delayed version of system (1) could also exhibit chaotic behaviors, such as time-delayed Lorenz system [19] and time-delayed Rossler system [21], etc. To consider the isochronal synchronization between chaotic and time-delayed chaotic systems, take the drive system as follows

$$\dot{y}=F(y){\theta }_r+G(y-\tau ){\beta }_r+f(y).$$

(2)

The response system is

$$\dot{x}=F(x)\theta +G(x)\beta +f(x)+u,$$

(3)

where u = (u₁, u₂,..., u _n )^T∈ Rⁿis the control input to be determined later.

Now we need to design the controller u such that the chaotic system (1) could track the trajectory of time-delayed system (2). Define the error e = x - λ(t)y, where λ(t) = diag(λ₁(t), λ₂(t),...,λ _n (t)).

Definition 1. It is said that isochronal function projective synchronization occurs between systems (1) and (2) if there exists a diagonal function matrix λ(t) such that

$$\underset{t\to \infty }{\text{lim}}∥e∥=\underset{t\to \infty }{\text{lim}}∥x-\lambda \left(t\right)y∥=0.$$

To achieve the isochronal synchronization between (1) and (2) with different initial conditions, now the control input is chosen as

$$\begin{array}{ll}\hfill u& =-F\left(x\right)\theta -G\left(x\right)\beta -f\left(x\right)+\lambda \left(t\right)\left(F\left(y\right)\theta +G\left(y-\tau \right)\beta +f\left(y\right)\right)\\ +\dot{\lambda }\left(t\right)y-ke,\end{array}$$

(4)

where k = diag(k₁, k₂,..., k _n ), k _i > 0(i = 1, 2,..., n) are constants. Consequently, we get

$$\dot{e}=\lambda (t)F(y)(\theta -{\theta }_r)+\lambda (t)G(y-\tau )(\beta -{\beta }_r)-ke.$$

(5)

The parameter updating laws for θ _r , β _r are chosen as

$$\left\{\begin{array}{c}{\dot{\theta }}_r=\lambda \left(t\right)eF\left(y\right),\hfill \\ {\dot{\beta }}_r=\lambda \left(t\right)eG\left(y-\tau \right),\hfill \end{array}\right.$$

(6)

then the synchronization result follows immediately.

Theorem 1. Isochronal function projective synchronization between systems (1) and (2) will occur under the control (4) and parameter updating laws (6).

Proof. Take the Lyapunov function

$$V=\frac{1}{2}\left(e^{T}e+e_{\theta }^T{e}_{\theta }+e_{\beta }^T{e}_{\beta }\right),$$

(7)

where e _θ = θ - θ _r , e _β = β - β _r . The time derivative of V along the trajectory of error system (5) is

$$\begin{array}{c}\dot{V}=e^T\dot{e}+e_{\theta }^T{\dot{e}}_{\theta }+e_{\beta }^T{\dot{e}}_{\beta }\\ =e^T\dot{e}+e_{\theta }^T(-{\dot{\theta }}_r)+e_{\beta }^T(-{\dot{\beta }}_r).\end{array}$$

In view of systems (5) and (6), one has

$$\dot{V}=-\sum _{i=1}^n{k}_i{e}_i^2\le 0.$$

(8)

So by Lyapunov stability theory, e _i → 0 as t → ∞, i.e., the synchronization will occur.

Remark 1. When λ(t) = I, -I, the complete synchronization and anti-synchronization between (1) and (2) are achieved, respectively. When λ(t) = αI, diag(λ₁,..., λ _n ), then generalized projective synchronization and modified projective synchronization between (1) and (2) will happen, respectively.

Remark 2. Here structures of systems (1) and (2) are in the same form. Similarly, the synchronization result could also hold between chaotic and delayed chaotic systems with different structures under appropriate controllers and parameter updating laws.

3. Applications

3.1. FPS between Lorenz and delayed Lorenz systems

The delayed Lorenz system is taken as the drive system

$$\{\begin{array}{l}{\dot{y}}_1=a_r(y_2-y_1),\hfill \\ {\dot{y}}_2=b_r{y}_1-y_2-y_2{y}_3,\hfill \\ {\dot{y}}_3=y_1{y}_2-c_r{y}_3(t-\tau ),\hfill \end{array}$$

(9)

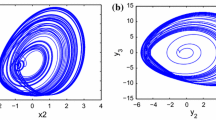
where a _r , b _r , c _r are uncertain parameters to be estimated. The system exhibits chaotic behaviors when a _r = 10, b _r = 28, $c_r=\frac{8}{3}$ and τ = 0.3, see Figure 1.

Figure 1

Chaotic attractor of time-delayed Lorenz system.

The response system is the Lorenz system with controllers

$$\{\begin{array}{l}{\dot{x}}_1=a(x_2-x_1)+u_1,\hfill \\ {\dot{x}}_2=b{x}_1-x_2-x_2{x}_3+u_2,\hfill \\ {\dot{x}}_3=x_1{x}_2-c{x}_3+u_3.\hfill \end{array}$$

(10)

Define the errors e _i = x _i - λ _i (t)y _i , i = 1, 2, 3. Choose the controllers as follows

$$\{\begin{array}{l}{u}_1=-a(x_2-x_1)+{\lambda }_1(t)a(y_2-y_1)+{\dot{\lambda }}_1(t)y_1-k_1{e}_1,\hfill \\ u_2=-b{x}_1+x_2+x_2{x}_3+{\lambda }_2(t)(b{y}_1-y_2-y_1{y}_3)+{\dot{\lambda }}_2(t)y_2-k_2{e}_2,\hfill \\ u_3=-x_1{x}_2+c{x}_3+{\lambda }_3(t)(y_1{y}_2-c{y}_3(t-\tau ))+{\dot{\lambda }}_3(t)y_3-k_3{e}_3,\hfill \end{array}$$

(11)

where k _i > 0, i = 1, 2, 3, then from systems (9), (10), and (11) one has

$$\{\begin{array}{l}{\dot{e}}_1={\lambda }_1(t)(a-a_r)(y_2-y_1)-k_1{e}_1,\hfill \\ {\dot{e}}_2={\lambda }_2(t)(b-b_r)y_1-k_2{e}_2,\hfill \\ {\dot{e}}_3=-{\lambda }_3(t)(c-c_r)y_3(t-\tau )-k_3{e}_3.\hfill \end{array}$$

(12)

The parameter updating laws are given by

$$\{\begin{array}{l}{\dot{a}}_r={\lambda }_1(t)(y_2-y_1)e_1,\hfill \\ {\dot{b}}_r={\lambda }_2(t)y_1{e}_2,\hfill \\ {\dot{c}}_r=-{\lambda }_3(t)y_3(t-\tau )e_3.\hfill \end{array}$$

(13)

Along the way similar to that of Theorem 1, one could arrive the following result.

Theorem 2. Isochronal function projective synchronization between Lorenz system (10) and delayed Lorenz system (9) will be realized under the controllers (11) and parameter updating laws (13).

3.2. FPS between hyper-chaotic Chen and delayed hyper-chaotic Chen systems

Consider the delayed hyper-chaotic Chen system

$$\{\begin{array}{l}{\dot{y}}_1=a_r(y_2-y_1)+y_4,\hfill \\ {\dot{y}}_2=d_r{y}_1-y_1{y}_3+c_r{y}_2(t-\tau ),\hfill \\ {\dot{y}}_3=b_r{y}_3-y_1{y}_2,\hfill \\ {\dot{y}}_4=p_4{y}_4+y_2{y}_3.\hfill \end{array}$$

(14)

When a _r = 35, b _r = 3, c _r = 12, d _r = 7, p _r = 0.5, and τ = 0.4, then the system displays chaotic behaviors, see Figure 2.

Figure 2

Chaotic attractor of time-delayed hyper-chaotic Chen system.

The response system is the hyper-chaotic Chen system with controllers

$$\{\begin{array}{l}{\dot{x}}_1=a(x_2-x_1)+x_4+u_1,\hfill \\ {\dot{x}}_2=d{x}_1-x_1{x}_3+c{x}_2+u_2,\hfill \\ {\dot{x}}_3=b{x}_3-x_1{x}_2+u_3,\hfill \\ {\dot{x}}_4=p{x}_4+x_2{x}_3+u_4.\hfill \end{array}$$

(15)

Define the errors e _i = x _i - λ _i (t)y _i , i = 1, 2, 3, 4. Choose the controllers as follows

$$\{\begin{array}{l}{u}_1=-a(x_2-x_1)-x_4+{\lambda }_1(t)(a(y_2-y_1)+y_4)+{\dot{\lambda }}_1(t)y_1-k_1{e}_1,\hfill \\ \begin{array}{l}{u}_2=-d{x}_1+x_1{x}_3-c{x}_2+{\lambda }_2(t)(d{y}_1-y_1{y}_3+c_2{y}_2(t-\tau ))\\ +{\dot{\lambda }}_2(t)y_2-k_2{e}_2,\end{array}\hfill \\ u_3=-x_1{x}_2+b{x}_3+{\lambda }_3(t)(y_1{y}_2-b{y}_3)+{\dot{\lambda }}_3(t)y_3-k_3{e}_3,\hfill \\ u_4=-p_4{y}_4-x_2{x}_3+{\dot{\lambda }}_4(t)y_4+{\lambda }_4(t)(p{y}_4+y_2{y}_3)-k_4{e}_4,\hfill \end{array}$$

(16)

where k _i > 0, i = 1, 2, 3, 4, then from systems (14), (15), and (16) one has

$$\{\begin{array}{l}{\dot{e}}_1={\lambda }_1(t)(a-a_r)(y_2-y_1)-k_1{e}_1,\hfill \\ {\dot{e}}_2={\lambda }_2(t)(c-c_r)y_2(t-\tau )+{\lambda }_2(t)(d-d_r)y_1-k_2{e}_2,\hfill \\ {\dot{e}}_3=-{\lambda }_3(t)(b-b_r)y_3-k_3{e}_3,\hfill \\ {\dot{e}}_4={\lambda }_4(t)(p-p_4)y_4-k_4{e}_4.\hfill \end{array}$$

(17)

The parameter updating laws are given by

$$\{\begin{array}{l}{\dot{a}}_r={\lambda }_1(t)(y_2-y_1)e_1,\hfill \\ {\dot{b}}_r=-{\lambda }_3(t)y_3{e}_3,\hfill \\ {\dot{c}}_r={\lambda }_2(t)y_2(t-\tau )e_2,\hfill \\ {\dot{d}}_r={\lambda }_2(t)y_1{e}_2,\hfill \\ {\dot{p}}_r={\lambda }_4(t)y_4{e}_4.\hfill \end{array}$$

(18)

As a result, the synchronization between (14) and (15) will happen.

Theorem 3. Isochronal function projective synchronization between hyper-chaotic Chen system (15) and delayed hyper-chaotic Chen system (14) will be achieved under the controllers (16) and parameter updating laws (18).

The proof is similar to that of Theorem 1.

3.3. Numerical simulations

The initial conditions for systems (9) and (10) are respectively chosen as (y₁(0), y₂(0), y₃(0)) = (1,-3,2) and (x₁(0), x₂(0), x₃(0)) = (-1,3,-2), and let τ = 0.3. The scaling functions are λ₁ (t) = sin(t), λ₂(t) = cos(t), λ₃(t) = - sin(t). Moreover, (k₁, k₂, k₃) = (1, 3, 2). The simulation results are shown in Figure 3. Note that the error variables e₁, e₂, e₃ tend to zero and the estimated values of unknown parameters a _r , b _r , c _r converge to $10,28,\frac{8}{3}$, respectively.

Figure 3

Time evolution of errors and estimated values of unknown parameters.

The initial conditions for systems (14) and (15) are respectively chosen as (y₁(0), y₂(0), y₃(0), y₄(0)) = (-3,4,-2,-2) and (x₁(0), x₂(0), x₃(0), x₄(0)) = (3,-4,2,2), and let τ = 0.3. The scaling functions are λ₁(t) = sin(t), λ₂(t) = -cos(t), λ₃(t) = cos(t), λ₄(t) = -sin(t). Moreover, the control gains are chosen as (k₁, k₂, k₃, k₄) = (7, 5, 5, 5). The simulation results are shown in Figures 4 and 5. Note that the error variables tend to zero and the estimated values of unknown parameters a _r , b _r , c _r , d _r , p _r converge to 35, 3, 12, 7, 0.5, respectively.

Figure 4

Time evolution of error variables of systems (18).

Figure 5

Time evolution of unknown parameters of system (19).

4. Conclusions

In this article, function projective synchronization between chaotic and time-delayed chaotic systems with unknown parameters is investigated. Adaptive synchronization scheme is proposed by designing appropriate controllers and parameter updating laws. Based on Lyapunov stability theory, synchronization results are obtained. The method is applied to Lorenz and hyper-chaotic Chen systems, respectively. Corresponding numerical simulations show the effectiveness of the method proposed. In existing literatures results about synchronization between chaotic and time-delayed chaotic systems are still few. So the obtained will be helpful in synchronizing chaotic and time-delayed chaotic systems.