Almost periodic dynamics of a discrete Nicholson’s blowflies model involving a linear harvesting term

Abstract

We consider a discrete Nicholson’s blowflies model involving a linear harvesting term. Under appropriate assumptions, sufficient conditions are established for the existence and exponential convergence of positive almost periodic solutions of this model. To expose the effectiveness of the main theorems, we support our result by a numerical example.

MSC:39A11.

1 Introduction

In [1], Gurney et al. proposed the following nonlinear autonomous delay equation:

$$x^{\mathrm{\prime }}(t)=-\alpha x(t)+\beta x(t-\tau )e^{-\lambda x(t-\tau )},\alpha ,\beta ,\tau ,\lambda \in (0,\mathrm{\infty })$$

(1.1)

to describe the population of the Australian sheep blowfly and to agree with the experimental data obtained by Nicholson in [2]. Here $x(t)$ is the size of the population at time t, β is the maximum per capita daily egg production, $1/\lambda$ is the size at which the blowfly population reproduces at its maximum rate, α is the per capita daily adult death rate, and τ is the generation time. Equation (1.1) is recognized in the literature as Nicholson’s blowflies model. The dynamical behavior of solutions of this model and its various modifications have been extensively studied by many authors during the last couple of decades. For more details, we suggest to the readers that they consult [3–18].

Biologists have proposed that the process of harvesting population is of great significance in the exploitation of biological resources, i.e., in fishery, forestry and wildlife management. This justification has attracted the attention of many mathematicians who are interested in studying the dynamic behavior of population models governed by differential or difference equations [19, 20]. In their recent paper [21], in particular, Berezansky et al. have put forward a question about the asymptotic behavior of the well-known Nicholson’s blowflies model involving a linear harvesting term of the form

$$x^{\mathrm{\prime }}(t)=-\alpha x(t)+\beta x(t-\tau )e^{-\lambda x(t-\tau )}-Hx(t-\sigma ),\alpha ,\beta ,\tau ,\lambda ,\sigma ,H\in (0,\mathrm{\infty }).$$

(1.2)

Recently, there have appeared many results concerning the investigation of periodic and almost periodic behaviors of system (1.2) via employing several utilities such as fixed-point theorems and the coincidence degree theory [22–25, 27, 28].

The delay difference equation

$$\mathrm{\Delta }x(n)=-\alpha x(n)+\beta x(n-\tau )e^{-\gamma x(n-\tau )},\alpha ,\beta ,\tau ,\lambda \in (0,\mathrm{\infty })$$

is a discrete analogue of the delay differential equation (1.1). For the purpose of convenience, however, we shall consider a discrete Nicholson’s blowflies model involving a linear harvesting term of the form

$$\mathrm{\Delta }x(n)=-\alpha (n)x(n+1)+\beta (n)x(n-\tau (n))e^{-\gamma (n)x(n-\tau (n))}-H(n)x(n-\sigma (n)),$$

(1.3)

where $n\in \mathbb{Z}$ and $\alpha ,\beta ,\gamma ,\tau ,\sigma ,H:\mathbb{Z}\to [0,\mathrm{\infty })$ are almost periodic sequences.

A primary purpose of this paper is to study the almost periodic dynamics of equation (1.3). We shall employ the contraction mapping principle to establish sufficient conditions for the existence of an almost periodic solution for (1.3). By constructing an appropriate Lyapunov functional, we also prove that the solutions of (1.3) converge exponentially to an almost periodic solution. We provide a numerical example to illustrate the effectiveness of the main theorems. To the best of authors’ knowledge, no paper regarding the investigation of almost periodicity of equation (1.3) has been published. Thus, our paper is different and presents a new approach.

2 Preliminaries

For a bounded sequence g defined on $\mathbb{Z}$, we define $g^{+}$ and $g^{-}$ as follows:

$$g^{+}=\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}g(n)\text{and}{g}^{-}=\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}g(n).$$

In the sequel, we assume that

$${\alpha }^{-}>0,{\beta }^{-}>0,{\gamma }^{-}>0$$

(2.1)

and

$$r=max\{{\tau }^{+},{\sigma }^{+}\}>0.$$

(2.2)

Let $I=\{-r,-r+1,\dots ,-1,0\}$, $C=\{\phi :I\to \mathbb{Z}\}$ and $C^{+}=\{\phi \in C:\phi \ge 0,\phi (0)>0\}$. For each $\phi \in C$, we define the norm of φ as ${\parallel \phi \parallel }_0={max}_{s\in I}|\phi |$. Denote $x_n=x(n+s)$ for all $s\in I$. For any $\phi \in C^{+}$, it is easy to see that there is a unique solution $x(n,0,\phi )$ of (1.3) with

$$x_0=\phi$$

(2.3)

and $x(n,0,\phi )>0$ for all $n\in \mathbb{Z}$.

Definition 1 A sequence $f(n)$ is said to be almost periodic if for $ϵ>0$, there is a constant $l(ϵ)>0$ such that in any interval of length $l(ϵ)$ there exists a number $\overline{\tau }\in \mathbb{Z}$ such that the inequality

$$|f(n+\overline{\tau })-f(n)|<ϵ$$

is satisfied for all $n\in \mathbb{Z}$.

The following basic results are essential for proving the main results in Section 3. They were provided in [26] for arbitrary time scale $\mathbb{T}$. If $\mathbb{T}=\mathbb{Z}$, then these results can be formulated as follows.

Theorem 1 ([26])

Let $f:\mathbb{Z}\to \mathbb{R}$ be an almost periodic sequence, then $f(n)$ is bounded on $\mathbb{Z}$.

Theorem 2 ([26])

If $f,g:\mathbb{Z}\to \mathbb{R}$ are almost periodic sequences, then $f+g$ and fg are almost periodic.

Theorem 3 ([26])

If $f:\mathbb{Z}\to \mathbb{R}$ is an almost periodic sequence, then $F(n)$ is almost periodic if and only if $F(n)$ is bounded on $\mathbb{Z}$ where $F(n)={\sum }_{k=0}^{n-1}f(k)$.

Theorem 4 ([26])

If $f:\mathbb{Z}\to \mathbb{R}$ is an almost periodic sequence and $F(\cdot )$ is defined on the value field of $f(n)$, then $F\circ f$ is almost periodic.

We assume that

A.1 There exist two constants ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ such that

$${\mathrm{\Gamma }}_1>{\mathrm{\Gamma }}_2,{\left(\frac{\beta }{\gamma }\right)}^{+}\frac{1}{{\alpha }^{-}e}<{\mathrm{\Gamma }}_1\text{and}\frac{{\beta }^{-}}{{\alpha }^{+}}{\mathrm{\Gamma }}_1{e}^{-{\gamma }^{+}{\mathrm{\Gamma }}_1}-\frac{H^{+}{\mathrm{\Gamma }}_1}{{\alpha }^{+}}>{\mathrm{\Gamma }}_2\ge \frac{1}{{\gamma }^{-}}.$$

The following result tells that every solution of (1.3) persists.

Lemma 1 Let A.1 hold. Then for $\phi \in C^0:=\{\phi :{\mathrm{\Gamma }}_2<\phi (n)<{\mathrm{\Gamma }}_1,\mathrm{\forall }n\in I\}$, the solution $x(n,n_0,\phi )$ of (1.3) and (2.3) satisfy

$${\mathrm{\Gamma }}_2<x(n,n_0,\phi )<{\mathrm{\Gamma }}_1,\mathrm{\forall }n\in [n_0,\mathrm{\infty }).$$

(2.4)

Proof Set $x(n)=x(n,n_0,\phi )$. Let $[n_0,T)\subseteq [n_0,\mathrm{\infty })$ be an interval such that

$$x(n)>0,\mathrm{\forall }n\in [n_0,T).$$

(2.5)

We claim that

$$0<x(n)<{\mathrm{\Gamma }}_1,\mathrm{\forall }n\in [n_0,T).$$

(2.6)

For the sake of contradiction, we assume that (2.6) is not true. Then, one can find $n_1\in (n_0,T)$ such that

$$x(n_1+1)\ge {\mathrm{\Gamma }}_1\text{and}0<x(n)<{\mathrm{\Gamma }}_1,\mathrm{\forall }n\in [n_0-r,n_1+1).$$

(2.7)

In view of (1.3), A.1, (2.7) and the fact that ${sup}_{u\ge 0}u{e}^{-u}=\frac{1}{e}$, we have

$$\begin{array}{rcl}0& \le & \mathrm{\Delta }x(n_1)\\ =& -\alpha (n_1)x(n_1+1)+\beta (n_1)x(n_1-\tau (n_1))e^{-\gamma (n_1)x(n_1-\tau (n_1))}-H(n_1)x(n_1-\sigma (n_1))\\ =& -\alpha (n_1)x(n_1+1)+\frac{\beta (n_1)}{\gamma (n_1)}\gamma (n_1)x(n_1-\tau (n_1))e^{-\gamma (n_1)x(n_1-\tau (n_1))}\\ -H(n_1)x(n_1-\sigma (n_1))\\ \le & -{\alpha }^{-}x(n_1+1)+{\left(\frac{\beta }{\gamma }\right)}^{+}\frac{1}{e}\\ \le & {\alpha }^{-}[-{\mathrm{\Gamma }}_1+{\left(\frac{\beta }{\gamma }\right)}^{+}\frac{1}{{\alpha }^{-}e}]\\ <& 0,\end{array}$$

which is a contradiction, and this implies that (2.6) holds. Next, we show that

$$x(n)>{\mathrm{\Gamma }}_2,\mathrm{\forall }n\in [n_0,T).$$

(2.8)

On the contrary, assume that there exists $n_2\in (n_0,T)$ such that

$$x(n_2+1)\le {\mathrm{\Gamma }}_2,\text{and}x(n)>{\mathrm{\Gamma }}_2,\mathrm{\forall }n\in [n_0-r,n_2+1).$$

(2.9)

In virtue of A.1 and (2.6), we obtain

$${\mathrm{\Gamma }}_2<x(n)<{\mathrm{\Gamma }}_1,{\gamma }^{+}x(n)\ge {\gamma }^{+}\frac{1}{{\gamma }^{-}}\ge 1,\mathrm{\forall }n\in [n_0-r,n_2+1).$$

(2.10)

In view of (1.3), A.1, (2.9), (2.10) and the fact that ${min}_{1\le u\le \delta }u{e}^{-u}=\delta e^{-\delta }$, we have

$$\begin{array}{rcl}0& \ge & \mathrm{\Delta }x(n_2)\\ =& -\alpha (n_2)x(n_2+1)+\beta (n_2)x(n_2-\tau (n_2))e^{-\gamma (n_2)x(n_2-\tau (n_2))}-H(n_2)x(n_2-\sigma (n_2))\\ =& -\alpha (n_2)x(n_2+1)+\frac{\beta (n_2)}{\gamma (n_2)}\gamma (n_2)x(n_2-\tau (n_2))e^{-\gamma (n_2)x(n_2-\tau (n_2))}\\ -H(n_2)x(n_2-\sigma (n_2))\\ \ge & -{\alpha }^{+}{\mathrm{\Gamma }}_2+\frac{{\beta }^{-}}{{\gamma }^{+}}{\gamma }^{+}{\mathrm{\Gamma }}_1{e}^{-{\gamma }^{+}{\mathrm{\Gamma }}_1}-H^{+}{\mathrm{\Gamma }}_1\\ \ge & {\alpha }^{+}[-{\mathrm{\Gamma }}_2+\frac{{\beta }^{-}}{{\alpha }^{+}}{\mathrm{\Gamma }}_1{e}^{-{\gamma }^{+}{\mathrm{\Gamma }}_1}-\frac{H^{+}{\mathrm{\Gamma }}_1}{{\alpha }^{+}}]>0,\end{array}$$

which is a contradiction, and this implies that (2.8) holds. In view of (2.6) and (2.8), it follows that relation (2.4) is true. Hence the proof is complete. □

3 The main results

Consider the linear difference system

$$x(n+1)=A(n)x(n),$$

(3.1)

where $x\in {\mathbb{Z}}^m$, and $A:\mathbb{Z}\to {\mathbb{Z}}^{m\times m}$ is a matrix sequence. In what follows, we denote by $\parallel \cdot \parallel$ any convenient norm either of a vector or of a matrix.

Definition 2 The difference system (3.1) is said to possess an exponential dichotomy on $\mathbb{Z}$ if there exists a projection P, that is, an $m\times m$ matrix P such that $P^2=P$, and constants $K>0$, $\nu >0$ such that

$$\begin{array}{c}\parallel X(r)P{X}^{-1}(s+1)\parallel \le K{\left(\frac{1}{1+\nu }\right)}^{r-s-1},r\ge s,\hfill \\ \parallel X(r)(I-P)X^{-1}(s+1)\parallel \le K{\left(\frac{1}{1+\nu }\right)}^{s+1-r},s\ge r,\hfill \end{array}$$

where $X(t)$ is the fundamental solution matrix of (3.1) and $r,s\in \mathbb{Z}$.

Consider the following almost periodic difference system:

$$x(n+1)=A(n)x(n)+f(n),$$

(3.2)

where $A:\mathbb{Z}\to {\mathbb{Z}}^{m\times m}$ is an almost periodic matrix sequence and $f:\mathbb{Z}\to {\mathbb{Z}}^m$ is an almost periodic vector sequence.

Theorem 5 If the linear system (3.1) admits an exponential dichotomy, then system (3.2) has a bounded solution $x(n)$ in the form

$$x(n)=\sum _{k=-\mathrm{\infty }}^{n-1}X(n)P{X}^{-1}(k+1)f(k)-\sum _{k=n}^{\mathrm{\infty }}X(n)(I-P)X^{-1}(k+1)f(k),$$

(3.3)

where $X(t)$ is the fundamental solution matrix of (3.1).

Proof By direct substitution, we obtain

$$\begin{array}{rcl}x(n+1)-A(n)x(n)& =& \sum _{k=-\mathrm{\infty }}^{n}X(n+1)P{X}^{-1}(k+1)f(k)\\ -\sum _{k=n+1}^{\mathrm{\infty }}X(n+1)X^{-1}(k+1)f(k)\\ +\sum _{k=n+1}^{\mathrm{\infty }}X(n+1)P{X}^{-1}(k+1)f(k)\\ -A(n)\sum _{k=-\mathrm{\infty }}^{n-1}X(n)P{X}^{-1}(k+1)f(k)\\ +A(n)\sum _{k=n}^{\mathrm{\infty }}X(n)X^{-1}(k+1)f(k)\\ -A(n)\sum _{k=n}^{\mathrm{\infty }}X(n)P{X}^{-1}(k+1)f(k).\end{array}$$

It follows that

$$\begin{array}{rcl}x(n+1)-A(n)x(n)& =& X(n+1)P{X}^{-1}(n+1)f(n)-A(n)X(n)P{X}^{-1}(n+1)f(n)\\ +A(n)X(n)X^{-1}(n+1)f(n)=f(n).\end{array}$$

Moreover, we have

$$\begin{array}{rcl}\parallel x(n)\parallel & =& \underset{n\in \mathbb{Z}}{sup}|\sum _{k=-\mathrm{\infty }}^{n-1}X(n)P{X}^{-1}(k+1)f(k)-\sum _{k=n}^{\mathrm{\infty }}X(n)(I-P)X^{-1}(k+1)f(k)|\\ \le & \underset{n\in \mathbb{Z}}{sup}\left(\right|\sum _{k=-\mathrm{\infty }}^{n-1}X(n)P{X}^{-1}(k+1)|+|\sum _{k=n}^{\mathrm{\infty }}X(n)(I-P)X^{-1}(k+1)\left|\right)K\parallel f\parallel \\ \le & \left(\right|\sum _{k=-\mathrm{\infty }}^{n-1}{\left(\frac{1}{1+\nu }\right)}^{n-k-1}|+|\sum _{k=n}^{\mathrm{\infty }}{\left(\frac{1}{1+\nu }\right)}^{k+1-n}\left|\right)K\parallel f\parallel \\ \le & (\frac{1+\nu }{\nu }+\frac{1}{\nu })K\parallel f\parallel =\frac{2+\nu }{\nu }K\parallel f\parallel ,\end{array}$$

where $\parallel \cdot \parallel ={sup}_{t\in \mathbb{Z}}|\cdot |$. By Theorem 1, $x(n)$ is a bounded solution of system (3.2). The proof is complete. □

Theorem 6 ([26])

Let $\alpha (n)>0$ be an almost periodic sequence on $\mathbb{Z}$ and

$$\underset{n\in \mathbb{Z}}{inf}\frac{\alpha (n)}{1+\alpha (n)}>0,$$

(3.4)

then the linear system

$$\mathrm{\Delta }x(n)=-\alpha (n)x(n+1)$$

(3.5)

admits an exponential dichotomy on $\mathbb{Z}$.

Set

$$\mathcal{B}=\{\phi :\phi \text{ is an almost periodic sequence on }\mathbb{Z}\}.$$

If we define the norm ${\parallel \phi \parallel }_{\mathcal{B}}$ =${sup}_{n\in \mathbb{Z}}|\phi (n)|$, for any $\phi \in \mathcal{B}$, then one can easily deduce that $\mathcal{B}$ is a Banach space.

We assume that

A.2 $\frac{{\beta }^{+}}{{\alpha }^{-}}\frac{1}{e^2}+\frac{H^{+}}{{\alpha }^{-}}<1$.

Theorem 7 Let A.1 and A.2 hold. Then, there exists a unique positive almost periodic solution of (1.3) in ${\mathcal{B}}^{\ast }:=\{\phi :\phi \in \mathcal{B},{\mathrm{\Gamma }}_2<\phi (n)<{\mathrm{\Gamma }}_1,\mathrm{\forall }n\in \mathbb{Z}\}$.

Proof For any $\varphi \in \mathcal{B}$, we consider an auxiliary equation

$$\mathrm{\Delta }x(n)=-\alpha (n)x(n+1)+\beta (n)\varphi (n-\tau (n))e^{-\gamma (n)\varphi (n-\tau (n))}-H(n)\varphi (n-\sigma (n)).$$

(3.6)

Since ${inf}_{n\in \mathbb{Z}}\frac{\alpha (n)}{1+\alpha (n)}>0$, it follows from Theorem 6 that the linear system

$$\mathrm{\Delta }x(n)=-\alpha (n)x(n+1)$$

(3.7)

admits an exponential dichotomy on $\mathbb{Z}$. By Theorem 5 and Theorem 6, we deduce that system (3.6) has a bounded solution of the form

$$\begin{array}{rcl}{x}^{\varphi }(n)& =& \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)[\beta (m)\varphi (m-\tau (m))e^{-\gamma (m)\varphi (m-\tau (m))}\\ -H(m)\varphi (m-\sigma (m))].\end{array}$$

(3.8)

In virtue of Theorem 2, Theorem 3, Theorem 4, and using the almost periodicity of ${\prod }_{r=m}^{n-1}(\frac{1}{1+\alpha (r)})$ and the fact that the uniform limit of almost periodic sequences is also almost periodic, we deduce that $x^{\varphi }$ is also almost periodic.

Define a mapping $T:\mathcal{B}\to \mathcal{B}$ by setting

$$T(\varphi (n))=x^{\varphi }(n),\mathrm{\forall }\varphi \in \mathcal{B}.$$

It is easy to see that ${\mathcal{B}}^{\ast }$ is a closed subset of $\mathcal{B}$. For any $\varphi \in {\mathcal{B}}^{\ast }$, we have

$$\begin{array}{rcl}{x}^{\varphi }(n)& \le & \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)\beta (m)\varphi (m-\tau (m))e^{-\gamma (m)\varphi (m-\tau (m))}\\ =& \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)\frac{\beta (m)}{\gamma (m)}\gamma (m)\varphi (m-\tau (m))e^{-\gamma (m)\varphi (m-\tau (m))}.\end{array}$$

By the fact that ${sup}_{u\ge 0}u{e}^{-u}=\frac{1}{e}$, we obtain

$$x^{\varphi }(n)\le \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)\frac{\beta (m)}{\gamma (m)e}$$

(3.9)

or

$$x^{\varphi }(n)\le \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+{\alpha }^{-}}\right){\left(\frac{\beta }{\gamma }\right)}^{+}\frac{1}{e}.$$

(3.10)

Using that ${\sum }_{m=-\mathrm{\infty }}^{n-1}{\prod }_{r=m}^{n-1}(\frac{1}{1+{\alpha }^{-}})=\frac{1}{{\alpha }^{-}}$, we end up with

$$x^{\varphi }(n)\le {\left(\frac{\beta }{\gamma }\right)}^{+}\frac{1}{{\alpha }^{-}e}\le {\mathrm{\Gamma }}_1,\mathrm{\forall }n\in \mathbb{Z}.$$

(3.11)

On the other hand, we have

$$\begin{array}{rcl}{x}^{\varphi }(n)& =& \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)[\beta (m)\varphi (m-\tau (m))e^{-\gamma (m)\varphi (m-\tau (m))}-H(m)\varphi (m-\sigma (m))]\\ \ge & \sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)[\frac{\beta (m)}{{\gamma }^{+}}{\gamma }^{+}\varphi (m-\tau (m))e^{-{\gamma }^{+}\varphi (m-\tau (m))}-H^{+}{\mathrm{\Gamma }}_1].\end{array}$$

By virtue of the fact that ${min}_{1\le u\le \kappa }u{e}^{-u}=\kappa e^{-\kappa }$, we obtain

$$x^{\varphi }(n)\ge \frac{{\beta }^{-}}{{\alpha }^{+}}{\mathrm{\Gamma }}_1{e}^{-{\gamma }^{+}{\mathrm{\Gamma }}_1}-\frac{H^{+}{\mathrm{\Gamma }}_1}{{\alpha }^{+}}\ge {\mathrm{\Gamma }}_2,\mathrm{\forall }n\in \mathbb{Z}.$$

This tells that the mapping T is a self-mapping from ${\mathcal{B}}^{\ast }$ to ${\mathcal{B}}^{\ast }$.

Let $\phi ,\psi \in {\mathcal{B}}^{\ast }$. Then

$$\begin{array}{rcl}{\parallel T(\phi )-T(\psi )\parallel }_{\mathcal{B}}& =& \underset{n\in \mathbb{Z}}{sup}|T(\phi (n))-T(\psi (n))|\\ =& \underset{n\in \mathbb{Z}}{sup}|\sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)\beta (m)[\phi (m-\tau (m))e^{-\gamma (m)\phi (m-\tau (m))}\\ -\psi (m-\tau (m))e^{-\gamma (m)\psi (m-\tau (m))}]\\ -H(m)[\phi (m-\sigma (m))-\psi (m-\sigma (m))]|\\ =& \underset{n\in \mathbb{Z}}{sup}\left|\sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+\alpha (r)}\right)\frac{\beta (m)}{\gamma (m)}\right[\gamma (m)\phi (m-\tau (m))e^{-\gamma (m)\phi (m-\tau (m))}\\ -\gamma (m)\psi (m-\tau (m))e^{-\gamma (m)\psi (m-\tau (m))}]\\ -H(m)[\phi (m-\sigma (m))-\psi (m-\sigma (m))]|.\end{array}$$

In virtue of the fact that ${sup}_{u\ge 1}|\frac{1-u}{e^u}|=\frac{1}{e^2}$, we observe that

$$\begin{array}{rcl}|x{e}^{-x}-y{e}^{-y}|& =& \left|\frac{1-(x+\theta (y-x))}{e^{x+\theta (y-x)}}\right||x-y|\\ \le & \frac{1}{e^2}|x-y|,x,y\in [1,\mathrm{\infty }),0<\theta <1.\end{array}$$

(3.12)

By A.1, we get

$$\gamma (m)\phi (m-\tau (m))\ge \gamma (m){\mathrm{\Gamma }}_2\ge \gamma (m)\frac{1}{{\gamma }^{-}}\ge 1,\mathrm{\forall }n\in \mathbb{Z}.$$

Therefore, by (1.3), (2.1) and (3.12), we have

$$\begin{array}{rcl}{\parallel T(\phi )-T(\psi )\parallel }_{\mathcal{B}}& \le & \underset{n\in \mathbb{Z}}{sup}\sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+{\alpha }^{-}}\right)\left[\frac{\beta (m)}{e^2}\right|\phi (m-\tau (m))-\psi (m-\tau (m))|\\ +H(m)|\phi (m-\sigma (m))-\psi (m-\sigma (m))|]\\ \le & \left(\underset{n\in \mathbb{Z}}{sup}\sum _{m=-\mathrm{\infty }}^{n-1}\prod _{r=m}^{n-1}\left(\frac{1}{1+{\alpha }^{-}}\right)\right)(\frac{\beta (m)}{e^2}+H^{+})\parallel \phi -\psi \parallel .\end{array}$$

Therefore, we end up with

$${\parallel T(\phi )-T(\psi )\parallel }_{\mathcal{B}}\le (\frac{{\beta }^{+}}{{\alpha }^{-}{e}^2}+\frac{H^{+}}{{\alpha }^{-}})\parallel \phi -\psi \parallel ,$$

which implies by A.2 that the mapping T is contractive on ${\mathcal{B}}^{\ast }$. Therefore, the mapping T possesses a unique fixed point ${\phi }^{\ast }\in {\mathcal{B}}^{\ast }$ such that $T{\phi }^{\ast }={\phi }^{\ast }$. Thus, ${\phi }^{\ast }$ is an almost periodic solution of (1.3) in the ${\mathcal{B}}^{\ast }$. The proof is complete. □

We assume that

A.3 ${\alpha }^{-}>1+\frac{{\beta }^{+}}{e^2}+H^{+}$.

Theorem 8 Let A.1 and A.3 hold. Further, assume $x^{\ast }(n)$ is a positive almost periodic solution of (1.3) in the set ${\mathcal{B}}^{\ast }$. Then, the solution $x(n,n_0,\phi )$ of (1.3) with $\phi \in C^0$ converges exponentially to $x^{\ast }(n)$ as $n\to \mathrm{\infty }$.

Proof Set $x(n)=x(n,n_0,\phi )$ and $y(n)=x(n)-x^{\ast }(n)$, where $n\in [n_0-r,\mathrm{\infty })$. Then

$$\begin{array}{rcl}\mathrm{\Delta }y(n)& =& -\alpha (n)y(n+1)+\beta (n)[x(n-\tau (n))e^{-\gamma (n)x(n-\tau (n))}\\ -x^{\ast }(n-\tau (n))e^{-\gamma (n)x^{\ast }(n-\tau (n))}]-H(n)y(n-\sigma (n)).\end{array}$$

(3.13)

The result of Lemma 1 tells that $x(n)$ is positive and bounded on $[n_0,\mathrm{\infty })$ and

$${\mathrm{\Gamma }}_2<x(n)<{\mathrm{\Gamma }}_1,\mathrm{\forall }n\in [n_0-r,\mathrm{\infty }).$$

(3.14)

Define a function $\mathrm{\Phi }(u)$ by setting

$$\mathrm{\Phi }(u)=e^u-{\alpha }^{-}+{\beta }^{+}\frac{1}{e^2}{e}^{u(r+1)}+H^{+}{e}^{u(r+1)},u\in [0,1].$$

(3.15)

It is clear that Φ is continuous on $[0,1]$. Then, by A.3 we have

$$\mathrm{\Phi }(0)=1-{\alpha }^{-}+\frac{{\beta }^{+}}{e^2}+H^{+}<0,$$

which implies that there exist two constants $\eta >0$ and $0<\lambda \le 1$ such that

$$\mathrm{\Phi }(\lambda )=e^{\lambda }-{\alpha }^{-}+{\beta }^{+}\frac{1}{e^2}{e}^{\lambda (r+1)}+H^{+}{e}^{\lambda (r+1)}<-\eta <0.$$

(3.16)

We consider the discrete Lyapunov functional

$$V(n)=|y(n)|e^{\lambda n}.$$

(3.17)

Calculating the difference of $V(n)$ along the solution $y(n)$ of (3.13), we have

$$\begin{array}{rcl}\mathrm{\Delta }V(n)& =& \mathrm{\Delta }\left(\right|y(n)\left|e^{\lambda n}\right)\\ =& \mathrm{\Delta }|y(n)|e^{\lambda (n+1)}+|y(n)|\mathrm{\Delta }{e}^{\lambda n}\\ \le & -\alpha (n)|y(n+1)|e^{\lambda (n+1)}+\beta (n)|x(n-\tau (n))e^{-\gamma (n)x(n-\tau (n))}\\ -x^{\ast }(n-\tau (n))e^{-\gamma (n)x^{\ast }(n-\tau (n))}|e^{\lambda (n+1)}\\ +H(n)\left|y(n-\sigma (n))\right|e^{\lambda (n+1)}+|y(n)|(e^{\lambda (n+1)}-e^{\lambda n})\\ \le & |y(n)|e^{\lambda (n+1)}-\alpha (n)|y(n+1)|e^{\lambda (n+1)}\\ +[\beta (n)|x(n-\tau (n))e^{-\gamma (n)x(n-\tau (n))}-x^{\ast }(n-\tau (n))e^{-\gamma (n)x^{\ast }(n-\tau (n))}|\\ +H(n)\left|y(n-\sigma (n))\right|]e^{\lambda (n+1)}\end{array}$$

(3.18)

for all $n\ge n_0$.

Let

$$M:=e^{\lambda n_0}\left(\underset{n\in [n_0,\mathrm{\infty })}{max}\right|\phi (n)-x^{\ast }(n)|+1),\mathrm{\forall }n\ge n_0.$$

Then, we claim that

$$V(n)=|y(n)|e^{\lambda n}<M,\mathrm{\forall }n\ge n_0.$$

(3.19)

Assume, on the contrary, that there exists $n_{\ast }>n_0$ such that

$$V(n_{\ast })\ge M\text{and}V(n)<M,\mathrm{\forall }n\in [n_0-r,n_{\ast }),$$

(3.20)

which implies that

$$V(n_{\ast })-M\ge 0\text{and}V(n)-M<0,\mathrm{\forall }n\in [n_0-r,n_{\ast }).$$

(3.21)

In virtue of (3.12), (3.18) and (3.20), we obtain

$$\begin{array}{rcl}0& \le & \mathrm{\Delta }(V(n_{\ast })-M)=\mathrm{\Delta }V(n_{\ast })\\ \le & |y(n_{\ast })|e^{\lambda (n_{\ast }+1)}-\alpha (n_{\ast })|y(n_{\ast }+1)|e^{\lambda (n_{\ast }+1)}\\ +[\beta (n_{\ast })|x(n_{\ast }-\tau (n_{\ast }))e^{-\gamma (n_{\ast })x(n_{\ast }-\tau (n_{\ast }))}-x^{\ast }(n_{\ast }-\tau (n_1))e^{-\gamma (n_{\ast })x^{\ast }(n_{\ast }-\tau (n_{\ast }))}|\\ +H(n_{\ast })\left|y(n_{\ast }-\sigma (n_{\ast }))\right|]e^{\lambda (n_{\ast }+1)}\\ \le & |y(n_{\ast })|e^{\lambda (n_{\ast }+1)}-\alpha (n_{\ast })|y(n_{\ast }+1)|e^{\lambda (n_{\ast }+1)}\\ +\frac{\beta (n_{\ast })}{e^2}\left|y(n_{\ast }-\tau (n_{\ast }))\right|e^{\lambda (n_{\ast }+1-\tau (n_{\ast }))}{e}^{\lambda \tau (n_{\ast })}\\ +H(n_{\ast })\left|y(n_{\ast }-\sigma (n_{\ast }))\right|e^{\lambda (n_{\ast }+1-\sigma (n_{\ast }))}{e}^{\lambda \sigma (n_{\ast })}\\ \le & (e^{\lambda }-{\alpha }^{-})M+\frac{{\beta }^{+}}{e^2}M{e}^{\lambda (r+1)}+H^{+}M{e}^{\lambda (r+1)}\\ =& [e^{\lambda }-{\alpha }^{-}+\frac{{\beta }^{+}}{e^2}{e}^{\lambda (r+1)}+H^{+}{e}^{\lambda (r+1)}]M.\end{array}$$

Thus,

$$e^{\lambda }-{\alpha }^{-}+\frac{{\beta }^{+}}{e^2}{e}^{\lambda (r+1)}+H^{+}{e}^{\lambda (r+1)}\ge 0,$$

which contradicts (3.16). Hence (3.19) holds. It follows that $|y(n)|<M{e}^{-\lambda n}$ for all $n\ge n_0$. The proof is complete. □

4 An example and concluding remark

In this section, we construct an example to demonstrate the results obtained in the previous sections. A concluding remark is also reported.

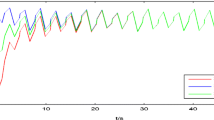
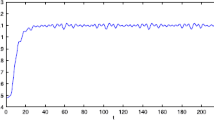
Example 1 Consider the following Nicholson’s blowflies model with a linear harvesting term of the form

$$\begin{array}{rcl}\mathrm{\Delta }x(n)& =& -(18+{cos}^{2}n)x(n+1)\\ +e^{e-1}(20+0.01|sin\sqrt{5}n|)x(n-e^{2|cos\sqrt{3}n|})e^{-x(n-e^{2|cos\sqrt{3}n|})}\\ -\frac{(18+{sin}^{2}n)|sinn|}{10\text{,}000}x(n-e^{2|cos\sqrt{5}n|}),\end{array}$$

(4.1)

where

$$\begin{array}{c}\alpha (n)=18+{cos}^{2}n,\beta (n)=e^{e-1}(20+0.01|sin\sqrt{5}n|),\hfill \\ \tau (n)=e^{2|cos\sqrt{3}n|},\gamma (n)=1\hfill \end{array}$$

and

$$\sigma (n)=e^{2|cos\sqrt{5}n|},H(n)=\frac{(18+{sin}^{2}n)|sinn|}{10\text{,}000}.$$

It is clear that

$${\alpha }^{-}=18,{\alpha }^{+}=19,{\beta }^{-}=20e^{e-1},{\beta }^{+}=20.01e^{e-1},{\gamma }^{+}={\gamma }^{-}=1$$

and

$${\tau }^{+}={\sigma }^{+}=e^2,H^{-}=0,H^{+}=\frac{19}{10\text{,}000}.$$

Thus, conditions (2.1) and (2.2) hold. Let ${\mathrm{\Gamma }}_1=e$ and ${\mathrm{\Gamma }}_2=1$. Then

$${\mathrm{\Gamma }}_1=e>{\mathrm{\Gamma }}_2=1,{\left(\frac{\beta }{\gamma }\right)}^{+}\frac{1}{{\alpha }^{-}e}\approx 1.140<e,\frac{{\beta }^{-}}{{\alpha }^{+}}{\mathrm{\Gamma }}_1{e}^{-{\gamma }^{+}{\mathrm{\Gamma }}_1}-\frac{H^{+}{\mathrm{\Gamma }}_1}{{\alpha }^{+}}\approx 1.05>1$$

and this shows that condition A.1 is satisfied. It remains to check conditions A.2 and A.3. However, one can see the validity of these conditions since

$$\frac{{\beta }^{+}}{{\alpha }^{-}}\frac{1}{e^2}+\frac{H^{+}}{{\alpha }^{-}}\approx 0.83<1\text{and}1+\frac{{\beta }^{+}}{e^2}+H^{+}\approx 16<18.$$

Therefore, we conclude that all assumptions of Theorem 7 and Theorem 8 are fulfilled. Hence, system (4.1) has a positive almost periodic solution $x^{\ast }$ in ${\mathcal{B}}^{\ast }=\{\phi :\phi \in \mathcal{B},1<\phi (n)<e,\mathrm{\forall }n\in \mathbb{Z}\}$. Moreover, if $\phi \in C^0$, then $x(n,n_0,\phi )$ converges exponentially to $x^{\ast }$ as $n\to \mathrm{\infty }$.

Remark 1 It is well known that the optimal management of renewable resources has direct relationship to the sustainable development of exploitation of population. One way to handle this is to study population models involving harvesting, dispersal or competition. Assuming that harvesting is a function of the delayed estimate of the true population, Nicholson’s blowflies model involving a linear harvesting term has been the object of recent research.

Following this trend, we study the almost periodic behavior of a discrete analogue of Nicholson’s blowflies model involving a linear harvesting term of form (1.3). It is worth mentioning here that most of the discrete analogues of Nicholson’s models investigated in the literature have involved a linear part of form $\mathrm{\Delta }x(n)=-\alpha (n)x(n)$. In this paper, however, we consider Nicholson’s model of form (1.3) to guarantee the convergence of the series appears in the solution representation (3.8).

A result concerning the persistence of the solutions is provided prior to proving the main theorems. Under the assumptions A.1-A.3, sufficient conditions are established for the existence and exponential convergence of positive almost periodic solutions of (1.3). Our approach is based on the contraction mapping principle as well as on the construction of an appropriate Lyapunov functional.

The results of this paper could be generalized to Nicholson’s model involving multiple delays and multiple linear harvesting terms. As Nicholson’s model under consideration is involving a linear harvesting term, one can easily figure out that some of the results reported in the literature might be no longer applicable for proving the existence and exponential convergence of almost periodic solutions of (1.3). This implies that the main theorems of this paper improve and extend some of previously obtained results.