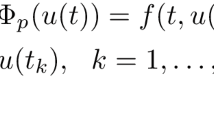Positive solutions for second order impulsive differential equations with Stieltjes integral boundary conditions

Abstract

In this paper, we study the existence of positive solutions for a singular second order impulsive differential equations with Stieltjes integral boundary conditions. By means of fixed point theorems, some results on the existence and multiplicity of positive solutions are obtained. Two examples are given to demonstrate the main results.

MSC:34B10, 34B15, 34B18, 34B37.

1 Introduction

In this paper, we consider the existence of positive solutions for the following second-order impulsive boundary value problem (IBVP for short)

$$\{\begin{array}{c}{x}^{″}(t)+a(t)x^{\prime }(t)+b(t)x(t)+h(t)f(t,x(t))=0,t\in J^{\prime },\hfill \\ -\mathrm{△}{x}^{\prime }{|}_{t=t_i}=I_i(x(t_i)),i=1,2,\dots ,m,\hfill \\ x(0)=\alpha [x],x(1)=\beta [x],\hfill \end{array}$$

(1.1)

where $J=[0,1]$, $0<t_1<t_2<\cdots <t_m<1$, $J^{\prime }=J\setminus \{t_1,t_2,\dots ,t_m\}$, $J_0=(0,t_1],J_1=(t_1,t_2],\dots ,J_m=(t_m,1)$, $f\in C(J\times {\mathbb{R}}^{+},{\mathbb{R}}^{+})$, $I_i\in C({\mathbb{R}}^{+},{\mathbb{R}}^{+})$, $i=1,2,\dots ,m$, ${\mathbb{R}}^{+}=[0,+\mathrm{\infty })$. $\mathrm{△}{x}^{\prime }{|}_{t=t_i}$ denotes the jump of $x^{\prime }$ at $t=t_i$, i.e.,

$$\mathrm{△}{x}^{\prime }{|}_{t=t_i}=x^{\prime }\left(t_i^{+}\right)-x^{\prime }\left(t_i^{-}\right),$$

where $x^{\prime }(t_i^{+})$ and $x^{\prime }(t_i^{-})$ represent the right-hand limit and the left-hand limit of $x^{\prime }$ at $t_i$, respectively. $\alpha [x]$, $\beta [x]$ are linear functionals on $C(I)$ given by

$$\alpha [x]={\int }_0^{1}x(t)dA(t),\beta [x]={\int }_0^{1}x(t)dB(t)$$

involving Stieltjes integrals with signed measures, that is, A, B are suitable functions of bounded variation.

Impulsive differential equations describe processes with sudden changes in their state at certain moments. The theory of impulse differential equations has been further developed significantly in recent years and has played a very important role in modern applied mathematical modeling of real world processes in physics, population dynamics, chemical technology, biotechnology and economics. For details, see [1–9] and references therein.

Recently, Feng and Xie [10] have dealt with the second order m-point boundary value problem with impulse effects

$$\{\begin{array}{c}-x^{″}(t)=f(t,x(t)),t\in J,t\ne t_i,\hfill \\ -\mathrm{△}{x}^{\prime }{|}_{t=t_i}=I_i(x(t_i)),i=1,2,\dots ,n,\hfill \\ x(0)={\sum }_{i=1}^{m-2}{a}_{i}x({\xi }_i),x(1)={\sum }_{i=1}^{m-2}{b}_{i}x({\xi }_i),\hfill \end{array}$$

where $a_i,b_i\in (0,1)$, $0<{\xi }_1<{\xi }_2<\cdots <{\xi }_{m-2}<1$, ${\sum }_{i=1}^{m-2}{b}_i{\xi }_i<1$, ${\sum }_{i=1}^{m-2}{a}_i(1-{\xi }_i)<1$. The existence results of one and two positive solutions are obtained based on the fixed point theorems in a cone.

For the case of $I_i=0$, $i=1,2,\dots ,m$, one of the special cases of problem (1.1) is the following multi-point boundary value problem

$$\{\begin{array}{c}{x}^{″}(t)+a(t)x^{\prime }(t)+b(t)x(t)+h(t)f(x(t))=0,t\in (0,1),\hfill \\ x(0)=0,x(1)={\sum }_{i=1}^{m-2}{a}_{i}x({\xi }_i),\hfill \end{array}$$

(1.2)

where $0<{\xi }_1<{\xi }_2<\cdots <{\xi }_{m-2}<1$. Boundary value problem (1.2) and related problems have been extensively studied in many papers in recent years (see [11–15] and references therein). The existence and multiplicity results of positive solutions are obtained by applying the Krasnosel’skii fixed-point theorem in cones, the Leggett-Williams fixed point theorem and the fixed point index theory. For example, Ma and Wang in [14] studied the existence of positive solutions to the nonlinear boundary-value problem

$$\{\begin{array}{c}{x}^{″}(t)+a(t)x^{\prime }(t)+b(t)x(t)+h(t)f(x(t))=0,t\in (0,1),\hfill \\ x(0)=0,x(1)=\alpha x(\eta ),\hfill \end{array}$$

(1.3)

where $a\in C(J)$, $b\in C(J,(-\mathrm{\infty },0))$, $0<\eta <1$ and $0<\alpha \varphi (\eta )<1$ are given, ϕ is the unique solution of the linear boundary value problem

$$\{\begin{array}{c}{x}^{″}(t)+a(t)x^{\prime }(t)+b(t)x(t)=0,t\in (0,1),\hfill \\ x(0)=0,x(1)=1.\hfill \end{array}$$

The authors established the existence of at least one positive solution of (1.3) if f is either superlinear or sublinear by applying the fixed point theorem in cones.

Inspired by the work of the above papers, the aim of this paper is to establish the existence and multiplicity of positive solutions for the IBVP (1.1). We discuss the boundary value problem with Stieltjes integral boundary conditions, i.e., the IBVP (1.1) which includes second order two-point, three-point, multi-point and nonlocal boundary value problems as special cases. Moreover, $\alpha [\cdot ]$ and $\beta [\cdot ]$ are two linear functions on $C[0,1]$ denoting the Stieltjes integrals, where $A,B$ are of bounded variation, that is dA and dB may change sign. By using the Krasnosel’skii fixed-point theorem and the Leggett-Williams fixed point theorem, some existence and multiplicity results of positive solutions are obtained.

This paper is organized as follows. In Section 2, we present some preliminaries and lemmas. Section 3 is devoted to the proof of the main results. In Section 4, two examples are given to demonstrate the validity of our main results.

2 Some preliminaries and lemmas

In this section, we first introduce some background definitions in a Banach space, present some basic lemmas, and then present the fixed point theorems that are to be used in the proof of the main results.

Let $P{C}^1(J,{\mathbb{R}}^{+})=\{x:x\in C(J,{\mathbb{R}}^{+}),x{|}_{J_i}\in C^1(J,{\mathbb{R}}^{+}),i=0,1,\dots ,m,\text{ and }{x}^{\prime }(t_i^{+})\text{ exists for }i=1,2,\dots ,m\}$ with the norm ${\parallel x\parallel }_{P{C}^1}=max\{{\parallel x\parallel }_{PC},{\parallel x^{\prime }\parallel }_{PC}\}$, where

$${\parallel x\parallel }_{PC}=\underset{t\in J}{sup}|x(t)|,{\parallel x^{\prime }\parallel }_{PC}=\underset{t\in J}{sup}|x^{\prime }(t)|.$$

Then $P{C}^1(J,{\mathbb{R}}^{+})$ is a Banach space. A function $x\in P{C}^1(J,{\mathbb{R}}^{+})\cap C^2(J^{\prime },\mathbb{R})$ is called a positive solution of problem (1.1) if it satisfies (1.1).

Lemma 2.1 [14]

Assume that $a\in C(J)$, $b\in C(J,(-\mathrm{\infty },0))$. Let ϕ and ψ be the unique solution of the following boundary value problem

$$\{\begin{array}{c}{\varphi }^{″}(t)+a(t){\varphi }^{\prime }(t)+b(t)\varphi (t)=0,t\in J,\hfill \\ \varphi (0)=0,\varphi (1)=1\hfill \end{array}$$

and

$$\{\begin{array}{c}{\psi }^{″}(t)+a(t){\psi }^{\prime }(t)+b(t)\psi (t)=0,t\in J,\hfill \\ \psi (0)=1,\psi (1)=0,\hfill \end{array}$$

respectively. Then ϕ is strictly increasing on J, ψ is strictly decreasing on J.

Throughout this paper, we adopt the following assumptions:

($H_1$) $a\in C(J)$, $b\in C(J,(-\mathrm{\infty },0))$, $k_1,k_4\in (0,1]$, $k_2,k_3\ge 0$, $k>0$, and

where

($H_2$) $h:(0,1)\to {\mathbb{R}}^{+}$ is a Lebesgue integral and $0<{\int }_0^{1}h(t)dt<+\mathrm{\infty }$, $I_i:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is continuous for $i=1,2,\dots ,m$.

($H_3$) $f:J\times {\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is continuous.

Remark 2.1 If dA and dB are two positive measures, then assumption ($H_1$) can be replaced by the weaker assumption

($H_1^{\prime }$) $a\in C(J)$, $b\in C(J,(-\mathrm{\infty },0))$, and $k_1>0$, $k_4>0$, $k>0$.

Lemma 2.2 Assume that ($H_1$) holds. Then for any $y\in L^1[0,1]$, the problem

$$\{\begin{array}{c}{x}^{″}(t)+a(t)x^{\prime }(t)+b(t)x(t)+y(t)=0,t\in J,t\ne t_i,\hfill \\ -\mathrm{△}{x}^{\prime }{|}_{t=t_i}=I_i\in \mathbb{R},i=1,2,\dots ,m,\hfill \\ x(0)=\alpha [x],x(1)=\beta [x],\hfill \end{array}$$

(2.1)

has a unique solution given by the following formula:

$$\begin{array}{rcl}x(t)& =& {\int }_0^{1}G(t,s)p(s)y(s)ds+\psi (t)\alpha [x]+\varphi (t)\beta [x]\\ +\psi (t)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i+\varphi (t)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i\end{array}$$

(2.2)

for $t\in J_i$, $i=0,1,\dots ,m$. Moreover, $x(t)\ge 0$ on J provided $y\ge 0$.

Proof By similar arguments in [5]. So it is omitted. □

Remark 2.2 If ($H_1$) holds, then for any $t,s\in J$, it is easy to testify that

$$\gamma (t)G(s,s)\le G(t,s)\le G(s,s),$$

(2.3)

where $\gamma (t)=min\{\varphi (t),\psi (t)\}$, $t\in J$. Let $\xi \in (0,t_1)$, $\eta \in (t_m,1)$, then

$$G(t,s)\ge \gamma G(s,s),t\in [\xi ,\eta ],s\in J,$$

(2.4)

where $\gamma ={min}_{\xi \le t\le \eta }\gamma (t)$.

Put

$$K=\{x\in PC(J,{\mathbb{R}}^{+}):\underset{\xi \le t\le \eta }{min}x(t)\ge \gamma {\parallel x\parallel }_{PC},\alpha [x]\ge 0,\beta [x]\ge 0\}.$$

Clearly, K is a cone of $PC(J,{\mathbb{R}}^{+})$. For any $r>0$, let $K_r=\{x\in K:{\parallel x\parallel }_{PC}<r\}$, $\partial K_r=\{x\in K:{\parallel x\parallel }_{PC}=r\}$ and ${\overline{K}}_r=\{x\in K:{\parallel x\parallel }_{PC}\le r\}$.

For $x\in C(J,{\mathbb{R}}^{+})$, we define two operators T and S by

$$Tx(t)=\psi (t)\alpha [x]+\varphi (t)\beta [x]+Fx(t)+Qx(t)$$

and

$$\begin{array}{rcl}Sx(t)& =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t),\end{array}$$

where

Lemma 2.3 Assume that ($H_1$)-($H_3$) hold. Then $T:K\to K$, $S:C(I,{\mathbb{R}}^{+})\to K$ are completely continuous.

Proof Problem (1.1) has a solution x if and only if x solves the operator equation $x=Tx$ in K. Let $x\in K$, by (2.3) and the monotonicity of ϕ, ψ, we have

$$\begin{array}{rcl}{\parallel Tx\parallel }_{PC}& \le & \alpha [x]+\beta [x]+{\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ +\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)).\end{array}$$

Moreover, by (2.3) and the definition of γ, we have

$$\begin{array}{rcl}\underset{\xi \le t\le \eta }{min}|Tx(t)|& \ge & \gamma (t)\alpha [x]+\gamma (t)\beta [x]+\gamma (t){\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ +\gamma (t)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\gamma (t)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \ge & \gamma {\parallel Tx\parallel }_{PC}.\end{array}$$

On the other hand,

$$\begin{array}{rcl}\alpha [Tx]& =& \alpha [\psi ]\alpha [x]+\alpha [\varphi ]\beta [x]+\alpha [Fx]+\alpha [Qx]\\ =& (1-k_1)\alpha [x]+k_2\beta [x]+{\int }_0^1({\int }_0^{1}G(t,s)p(s)h(s)f(s,x(s))ds)dA(t)\\ +(1-k_1)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+k_2\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ =& (1-k_1)\alpha [x]+k_2\beta [x]+{\int }_0^1{\mathcal{G}}_A(s)h(s)f(s,x(s))ds\\ +(1-k_1)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+k_2\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\ge 0,\\ \beta [Tx]& =& \beta [\psi ]\alpha [x]+\beta [\varphi ]\beta [x]+\beta [Fx]+\beta [Qx]\\ =& k_3\alpha [x]+(1-k_4)\beta [x]+{\int }_0^1({\int }_0^{1}G(t,s)p(s)h(s)f(s,x(s))ds)dB(t)\\ +k_3\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+(1-k_4)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ =& k_3\alpha [x]+(1-k_4)\beta [x]+{\int }_0^1{\mathcal{G}}_B(s)h(s)f(s,x(s))ds\\ +k_3\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+(1-k_4)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\ge 0.\end{array}$$

This shows that $T:K\to K$.

Now we consider the operator S. Similarly as for the operator T, we have

$$\begin{array}{rcl}{\parallel Sx\parallel }_{PC}& \le & k^{-1}(k_3+k_4)(\alpha [Fx]+\alpha [Qx])+k^{-1}(k_1+k_2)(\beta [Fx]+\beta [Qx])\\ +{\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ +\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)),\end{array}$$

and

$$\begin{array}{rcl}\underset{\xi \le t\le \eta }{min}|Sx(t)|& \ge & k^{-1}(k_3+k_4)\gamma (t)(\alpha [Fx]+\alpha [Qx])+k^{-1}(k_1+k_2)\gamma (t)(\beta [Fx]+\beta [Qx])\\ +\gamma (t){\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ +\gamma (t)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\gamma (t)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \ge & \gamma {\parallel Sx\parallel }_{PC}.\end{array}$$

Moreover,

$$\begin{array}{rcl}\alpha [Sx]& =& k^{-1}(k_3{k}_2+k_4(1-k_1))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1{k}_2+k_2(1-k_1))(\beta [Fx]+\beta [Qx])+\alpha [Fx]+\alpha [Qx]\\ =& k^{-1}{k}_4(\alpha [Fx]+\alpha [Qx])+k^{-1}{k}_2(\beta [Fx]+\beta [Qx])\ge 0,\end{array}$$

(2.5)

$$\begin{array}{rcl}\beta [Sx]& =& k^{-1}(k_3(1-k_4)+k_4{k}_3)(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1(1-k_4)+k_2{k}_3)(\beta [Fx]+\beta [Qx])+\beta [Fx]+\beta [Qx]\\ =& k^{-1}{k}_3(\alpha [Fx]+\alpha [Qx])+k^{-1}{k}_1(\beta [Fx]+\beta [Qx])\ge 0.\end{array}$$

(2.6)

This yields that $S:C(J,{\mathbb{R}}^{+})\to K$.

Next, by similar arguments in [16], one can prove that $T:K\to K$, $S:C(J,{\mathbb{R}}^{+})\to K$ are completely continuous. So we omit further details, and Lemma 2.3 is proved. □

Lemma 2.4 Assume that ($H_1$)-($H_3$) hold. Then operators T and S have the same fixed point in K.

Proof Let x be a fixed point of the operator S, i.e., $x=Sx$. Then by (2.5) and (2.6), we have

So we have

$$\alpha [Fx]+\alpha [Qx]=k_1\alpha [x]-k_2\beta [x],\beta [Fx]+\beta [Qx]=-k_3\alpha [x]+k_4\beta [x].$$

Then

$$\begin{array}{rcl}x(t)& =& Sx(t)\\ =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t)\\ =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(k_1\alpha [x]-k_2\beta [x])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(-k_3\alpha [x]+k_4\beta [x])+Fx(t)+Qx(t)\\ =& \psi (t)\alpha [x]+\varphi (t)\beta [x]+Fx(t)+Qx(t)=Tx(t).\end{array}$$

This implies that x also is a fixed point of the operator T.

On the other hand, let x be a fixed point of the operator T, i.e., $x=Tx$. Then

So we have

Therefore,

$$\begin{array}{rcl}x(t)& =& Tx(t)\\ =& \psi (t)\alpha [x]+\varphi (t)\beta [x]+Fx(t)+Qx(t)\\ =& \psi (t)k^{-1}[k_4(\alpha [Qx]+\alpha [Fx])+k_2(\beta [Fx]+\beta [Qx])]\\ +\varphi (t)k^{-1}[k_3(\alpha [Qx]+\alpha [Fx])+k_1(\beta [Fx]+\beta [Qx])]+Fx(t)+Qx(t)\\ =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t)=Sx(t).\end{array}$$

This implies that x is also a fixed point of the operator S. The proof is completed. □

Lemma 2.5 [17]

Let X be a real Banach space, K is a cone in X. Assume that ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ are two bounded open sets of X with $\theta \in {\mathrm{\Omega }}_1$ and ${\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$. Let $T:K\cap ({\overline{\mathrm{\Omega }}}_2\mathrm{\setminus }{\mathrm{\Omega }}_1)\to K$ be a completely continuous operator such that either

• (i) $\parallel Tx\parallel \le \parallel x\parallel$, $x\in K\cap \partial {\mathrm{\Omega }}_1$ and $\parallel Tx\parallel \ge \parallel x\parallel$, $x\in K\cap \partial {\mathrm{\Omega }}_2$, or

• (ii) $\parallel Tx\parallel \ge \parallel x\parallel$, $x\in K\cap \partial {\mathrm{\Omega }}_1$ and $\parallel Tx\parallel \le \parallel x\parallel$, $x\in K\cap \partial {\mathrm{\Omega }}_2$.

Then T has a fixed point in $K\cap ({\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1)$.

Lemma 2.6 [18, 19]

Let K be a cone in a real Banach space X, $K_c=\{x\in K:\parallel x\parallel <c\}$, φ is a nonnegative continuous concave functional on K such that $\phi (x)\le \parallel x\parallel$, for all $x\in {\overline{K}}_c$, and $K(\phi ,b,d)=\{x\in K:b\le \phi (x),\parallel x\parallel \le d\}$. Suppose that $T:{\overline{K}}_c\to {\overline{K}}_c$ is completely continuous and there exist positive constants $0<a<b<d\le c$ such that

($C_1$) $\{x\in K(\phi ,b,d):\phi (x)>b\}\ne \varphi$ and $\phi (Tx)>b$ for $x\in K(\phi ,b,d)$,

($C_2$) $\parallel Tx\parallel <a$ for $x\in {\overline{K}}_a$,

($C_3$) $\phi (Tx)>b$ for $x\in K(\phi ,b,c)$ with $\parallel Tx\parallel >d$.

Then T has at least three fixed points $x_1$, $x_2$ and $x_3$ with

$$\parallel x_1\parallel <a,b<\phi (x_2),a<\parallel x_3\parallel \mathit{\text{with}}\phi (x_3)<b.$$

Remark 2.3 If there holds $d=c$, then condition ($C_1$) of Lemma 2.6 implies condition ($C_3$) of Lemma 2.6.

3 Main results

Let

where ω denotes 0 or ∞. Let

(3.1)

(3.2)

and let the nonnegative continuous concave functional φ on the cone K be defined by

$$\phi (x)=\underset{\xi \le t\le \eta }{min}|x(t)|.$$

In this section, we apply Lemmas 2.5 and 2.6 to establish the existence of positive solutions for IBVP (1.1). Since operators T and S have the same fixed points (see Lemma 2.4), to prove the following theorems we always use the operator S instead of T.

Theorem 3.1 Assume that ($H_1$)-($H_3$) hold. In addition, suppose $f^0+{\sum }_{j=1}^m{I}_j^0=0$ and $max\{f_{\mathrm{\infty }},I_{1\mathrm{\infty }},\dots ,I_{m\mathrm{\infty }}\}=\mathrm{\infty }$ are satisfied, then IBVP (1.1) has at least one positive solution $x^{\ast }(t)$.

Proof From $f^0+{\sum }_{j=1}^m{I}_j^0=0$, there exists $r_1>0$ such that $f(t,u)<{\epsilon }_{1}u$, $I_j(u)<{\epsilon }_{1}u$ ($j=1,2,\dots ,m$) for all $t\in J$ and $0\le u\le r_1$, where ${\epsilon }_1>0$ satisfies

$${\epsilon }_1<min\{\frac{1}{2[L_1+\sigma (L_2+L_3)]},\frac{1}{2\sigma ({\sum }_{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)+{\sum }_{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i))}\}.$$

(3.3)

If $x\in {\overline{K}}_{r_1}$, then ${\parallel x\parallel }_{PC}\le r_1$. So we have $0\le x(t)\le r_1$, $t\in J$ and

(3.4)

(3.5)

(3.6)

(3.7)

(3.8)

(3.9)

So, by (3.4)-(3.9), for any $x\in \partial K_{r_1}$, $t\in J$, we have

$$\begin{array}{rcl}|Sx(t)|& =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t)\\ \le & k^{-1}(k_3+k_4)(\alpha [Fx]+\alpha [Qx])+k^{-1}(k_1+k_2)(\beta [Fx]+\beta [Qx])\\ +\underset{t\in J}{max}|Fx(t)|+\underset{t\in J}{max}|Qx(t)|\\ \le & k^{-1}(k_3+k_4)\alpha [Fx]+k^{-1}(k_1+k_2)\beta [Fx]+\underset{t\in J}{max}|Fx(t)|\\ +k^{-1}(k_3+k_4)((1-k_1)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +k_2\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)))\\ +k^{-1}(k_1+k_2)(k_3\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +(1-k_4)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)))\\ +\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \le & k^{-1}(k_3+k_4)L_2{\epsilon }_1{r}_1+k^{-1}(k_1+k_2)L_3{\epsilon }_1{r}_1+L_1{\epsilon }_1{r}_1\\ +k^{-1}(k_3+k_4)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +k^{-1}(k_1+k_2)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \le & {\epsilon }_1[L_1+\sigma (L_2+L_3)]r_1+{\epsilon }_1{r}_1\sigma [\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)]\\ <& r_1={\parallel x\parallel }_{PC},\end{array}$$

(3.10)

which means that

$${\parallel Sx\parallel }_{PC}\le {\parallel x\parallel }_{PC},x\in \partial K_{r_1}.$$

(3.11)

Next, consider $max\{f_{\mathrm{\infty }},I_{1\mathrm{\infty }},\dots ,I_{m\mathrm{\infty }}\}=\mathrm{\infty }$. Without loss of generality, we assume that $max\{f_{\mathrm{\infty }},I_{1\mathrm{\infty }},\dots ,I_{m\mathrm{\infty }}\}=f_{\mathrm{\infty }}$, which means that there exists ${\overline{r}}_2>0$ such that $f(t,u)>{\epsilon }_{2}u$ for all $t\in [\xi ,\eta ]$ and $u\ge {\overline{r}}_2$, where ${\epsilon }_2$ satisfies

$${\epsilon }_2>max\{\frac{1}{\gamma [L_1+\tau (L_2+L_3)]},\frac{1}{\gamma \tau ({\sum }_{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)+{\sum }_{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i))}\}.$$

(3.12)

Let $r_2\ge max\{2r_1,\frac{{\overline{r}}_2}{\gamma }\}$, then for any $x\in \partial K_{r_2}$, $t\in [\xi ,\eta ]$, we have

$$\begin{array}{rcl}|Sx(t)|& \ge & \underset{\xi \le t\le \eta }{min}(k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t))\\ \ge & \gamma k^{-1}(k_3+k_4)\alpha [Fx]+\gamma k^{-1}(k_1+k_2)\beta [Fx]\\ +\gamma {\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ \ge & \gamma [k^{-1}(k_3+k_4)L_2{\epsilon }_2{r}_2+k^{-1}(k_1+k_2)L_3{\epsilon }_2{r}_2+L_1{\epsilon }_2{r}_2]\\ \ge & \gamma {\epsilon }_2[L_1+\tau (L_2+L_3)]r_2\\ >& r_2={\parallel x\parallel }_{PC}.\end{array}$$

Consequently, we have

$${\parallel Sx\parallel }_{PC}\ge {\parallel x\parallel }_{PC},x\in \partial K_{r_2}.$$

(3.13)

Applying (i) of Lemma 2.5 to (3.11) and (3.13) yields that S has a fixed point $x^{\ast }:r_1\le {\parallel x^{\ast }\parallel }_{PC}\le r_2$. Thus it follows that IBVP (1.1) has a positive solution $x^{\ast }$. □

Theorem 3.2 Assume that ($H_1$)-($H_3$) hold. In addition, suppose $f^{\mathrm{\infty }}+{\sum }_{j=1}^m{I}_j^{\mathrm{\infty }}=0$ and $max\{f_0,I_{10},\dots ,I_{m0}\}=\mathrm{\infty }$ are satisfied, then IBVP (1.1) has at least one positive solution $x^{\ast }(t)$.

Proof Consider $max\{f_0,I_{10},\dots ,I_{m0}\}=\mathrm{\infty }$. Without loss of generality, we assume that $max\{f_0,I_{10},\dots ,I_{m0}\}=f_0$, which means that there exists $R_1>0$ such that $f(t,u)>{\epsilon }_{2}u$ for all $t\in [\xi ,\eta ]$ and $0\le u\le R_1$, where ${\epsilon }_2$ satisfies (3.12). Then for any $x\in \partial K_{R_1}$, $t\in [\xi ,\eta ]$, we have

$$\begin{array}{rcl}|Sx(t)|& \ge & \underset{\xi \le t\le \eta }{min}(k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t))\\ \ge & \gamma k^{-1}(k_3+k_4)\alpha [Fx]+\gamma k^{-1}(k_1+k_2)\beta [Fx]\\ +\gamma {\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ \ge & \gamma [k^{-1}(k_3+k_4)L_2{\epsilon }_2{R}_1+k^{-1}(k_1+k_2)L_3{\epsilon }_2{R}_1+L_1{\epsilon }_2{R}_1]\\ \ge & \gamma {\epsilon }_2[L_1+\tau (L_2+L_3)]r_2\\ >& R_1={\parallel x\parallel }_{PC},\end{array}$$

which yields that

$${\parallel Sx\parallel }_{PC}\ge {\parallel x\parallel }_{PC},x\in \partial K_{R_1}.$$

(3.14)

On the other hand, it follows from $f^{\mathrm{\infty }}+{\sum }_{j=1}^m{I}_j^{\mathrm{\infty }}=0$ that there exists $R_2:R_2>R_1$ such that $f(t,u)<{\epsilon }_{1}u$, $I_j(u)<{\epsilon }_{1}u$ ($j=1,2,\dots ,m$) for all $t\in J$ and $u\ge R_2$, where ${\epsilon }_1>0$ satisfies (3.3). Similar to (3.10), for any $x\in \partial K_{R_2}$, $t\in J$, we have

$$\begin{array}{rcl}|Sx(t)|& =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t)\\ \le & k^{-1}(k_3+k_4)(\alpha [Fx]+\alpha [Qx])+k^{-1}(k_1+k_2)(\beta [Fx]+\beta [Qx])\\ +\underset{t\in J}{max}|Fx(t)|+\underset{t\in J}{max}|Qx(t)|\\ \le & k^{-1}(k_3+k_4)\alpha [Fx]+k^{-1}(k_1+k_2)\beta [Fx]+\underset{t\in J}{max}|Fx(t)|\\ +k^{-1}(k_3+k_4)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +k^{-1}(k_1+k_2)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \le & {\epsilon }_1[L_1+\sigma (L_2+L_3)]R_2+{\epsilon }_1{R}_2\sigma [\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)]\\ <& R_2={\parallel x\parallel }_{PC},\end{array}$$

which means that

$${\parallel Sx\parallel }_{PC}\le {\parallel x\parallel }_{PC},x\in \partial K_{R_2}.$$

(3.15)

Applying (ii) of Lemma 2.5 to (3.14) and (3.15) yields that S has a fixed point $x^{\ast }:R_1\le {\parallel x^{\ast }\parallel }_{PC}\le R_2$. Thus it follows that IBVP (1.1) has a positive solution $x^{\ast }$. □

Theorem 3.3 Assume that ($H_1$)-($H_3$) hold. In addition, we suppose that there exist positive constants Γ, Λ and $a<b<c$ such that

where γ, $L_i$ ($i=1,2,3$) and σ, τ are defined by (2.4), (3.1) and (3.2), respectively, $M\ge 0$, $N\ge 0$, and

($S_1$) $f(t,u)\le \frac{c}{\mathrm{\Gamma }}$, for $(t,u)\in J\times [0,c]$, and

$$\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(u_i)+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(u_i)\le \frac{M}{\mathrm{\Gamma }}c,$$

for $u_i\in [0,c]$, $i=0,1,\dots ,m$.

($S_2$) $f(t,u)<\frac{a}{\mathrm{\Gamma }}$, for $(t,u)\in J\times [0,a]$, and

$$\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(u_i)+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(u_i)\le \frac{M}{\mathrm{\Gamma }}a,$$

for $u_i\in [0,a]$, $i=0,1,\dots ,m$.

($S_3$) $f(t,u)\ge \frac{b}{\mathrm{\Lambda }}$, for $(t,u)\in [\xi ,\eta ]\times [b,c]$, and

$$\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(u_i)+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(u_i)\ge \frac{N}{\mathrm{\Lambda }}b,$$

for $b\le u_i\le c$, $i=0,1,\dots ,m$.

Then IBVP (1.1) has at least three positive solutions $x_1$, $x_2$ and $x_3$ with

$${\parallel x_1\parallel }_{PC}<a,b<\underset{\xi \le t\le \eta }{min}|x_2(t)|<{\parallel x_2\parallel }_{PC}\le c$$

and

$$a<{\parallel x_3\parallel }_{PC},\underset{\xi \le t\le \eta }{min}|x_3(t)|<b.$$

Proof We shall show that all the conditions of Lemma 2.6 are satisfied.

First, if $x\in {\overline{K}}_c$, then ${\parallel x\parallel }_{PC}\le c$ and (3.4), (3.6), (3.7) are valid if $r_1$ is replaced by $\frac{c}{\mathrm{\Gamma }}$. From this and (3.5), (3.8) and (3.9), for any $x\in {\overline{K}}_c$, we have

$$\begin{array}{rcl}|Sx(t)|& =& k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t)\\ \le & k^{-1}(k_3+k_4)(\alpha [Fx]+\alpha [Qx])+k^{-1}(k_1+k_2)(\beta [Fx]+\beta [Qx])\\ +\underset{t\in J}{max}|Fx(t)|+\underset{t\in J}{max}|Qx(t)|\\ \le & k^{-1}(k_3+k_4)\alpha [Fx]+k^{-1}(k_1+k_2)\beta [Fx]+\underset{t\in J}{max}|Fx(t)|\\ +k^{-1}(k_3+k_4)((1-k_1)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +k_2\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)))\\ +k^{-1}(k_1+k_2)(k_3\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +(1-k_4)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)))\\ +\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \le & k^{-1}(k_3+k_4)\frac{L_2}{\mathrm{\Gamma }}c+k^{-1}(k_1+k_2)\frac{L_3}{\mathrm{\Gamma }}c+\frac{L_1}{\mathrm{\Gamma }}c\\ +k^{-1}(k_3+k_4)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +k^{-1}(k_1+k_2)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \le & \frac{1}{\mathrm{\Gamma }}[L_1+\sigma (L_2+L_3+M)]c<c,\end{array}$$

which means that ${\parallel Sx\parallel }_{PC}\le c,x\in {\overline{K}}_c$. Therefore, $S:{\overline{K}}_c\to {\overline{K}}_c$. By Lemma 2.3, we know that $S:{\overline{K}}_c\to {\overline{K}}_c$ is completely continuous.

Next, it follows from condition ($S_2$) that if $x\in {\overline{K}}_a$ then

$$\begin{array}{rcl}{\parallel Sx\parallel }_{PC}& \le & k^{-1}(k_3+k_4)(\alpha [Fx]+\alpha [Qx])+k^{-1}(k_1+k_2)(\beta [Fx]+\beta [Qx])\\ +\underset{t\in J}{max}|Fx(t)|+\underset{t\in J}{max}|Qx(t)|\\ \le & \sigma \frac{L_2}{\mathrm{\Gamma }}a+\sigma \frac{L_3}{\mathrm{\Gamma }}a+\frac{L_1}{\mathrm{\Gamma }}a+\sigma \sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))\\ +\sigma \sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \le & \frac{1}{\mathrm{\Gamma }}[L_1+\sigma (L_2+L_3+M)]a<a.\end{array}$$

So the condition ($C_2$) of Lemma 2.6 holds.

Now, we take $x(t)=\frac{b+c}{2}$, $t\in J$, then it is easy to see that $x(t)=\frac{b+c}{2}\in K(\phi ,b,c)$, and hence

$$\phi (x)=\underset{\xi \le t\le \eta }{min}|x(t)|=\frac{b+c}{2}>b.$$

Moreover, $\alpha [x]\ge 0$, $\beta [x]\ge 0$. This proves that $\{x\in K(\phi ,b,c):\phi (x)>b\}\ne \varphi$.

On the other hand, if $x\in K(\phi ,b,c)$, then $b\le x(t)\le c$, $t\in [\xi ,\eta ]$. By condition ($S_3$), we have

$$\begin{array}{rcl}\phi (Sx)& =& \underset{\xi \le t\le \eta }{min}|Sx(t)|\\ =& \underset{\xi \le t\le \eta }{min}(k^{-1}(k_3\varphi (t)+k_4\psi (t))(\alpha [Fx]+\alpha [Qx])\\ +k^{-1}(k_1\varphi (t)+k_2\psi (t))(\beta [Fx]+\beta [Qx])+Fx(t)+Qx(t))\\ \ge & \gamma k^{-1}(k_3+k_4)(\alpha [Fx]+\alpha [Qx])+\gamma k^{-1}(k_1+k_2)(\beta [Fx]+\beta [Qx])\\ +\gamma {\int }_0^{1}G(s,s)p(s)h(s)f(s,x(s))ds\\ +\gamma \sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\gamma \sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\\ \ge & \gamma \{k^{-1}(k_3+k_4)\frac{L_{2}b}{\mathrm{\Lambda }}+k^{-1}(k_1+k_2)\frac{L_{3}b}{\mathrm{\Lambda }}+\frac{L_{1}b}{\mathrm{\Lambda }}+k^{-1}(k_3+k_4)\\ \times ((1-k_1)\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+k_2\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)))\\ +\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))+k^{-1}(k_1+k_2)\\ \times (k_3\sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+(1-k_4)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i)))\}\\ =& \gamma \{k^{-1}(k_3+k_4)\frac{L_{2}b}{\mathrm{\Lambda }}+k^{-1}(k_1+k_2)\frac{L_{3}b}{\mathrm{\Lambda }}+\frac{L_{1}b}{\mathrm{\Lambda }}+k^{-1}(k_3+k_4)\\ \times \sum _{i=1}^j{\rho }^{-1}p(t_i)\varphi (t_i)I_i(x(t_i))+k^{-1}(k_1+k_2)\sum _{i=j+1}^m{\rho }^{-1}p(t_i)\psi (t_i)I_i(x(t_i))\}\\ \ge & \frac{1}{\mathrm{\Lambda }}\gamma (L_1+\tau (L_2+L_3+N))b\\ >& b,\end{array}$$

which implies that $\phi (Sx)>b$, for $x\in K(\phi ,b,c)$. This shows that condition ($C_1$) of Lemma 2.6 is also satisfied.

By Lemma 2.6 and Remark 2.3, IBVP (1.1) has at least three positive solutions $x_1,x_2$ and $x_3$ such that

$${\parallel x_1\parallel }_{PC}<a,b<\underset{\xi \le t\le \eta }{min}|x_2(t)|<{\parallel x_2\parallel }_{PC}\le c$$

and

$$a<{\parallel x_3\parallel }_{PC},\underset{\xi \le t\le \eta }{min}|x_3(t)|<b.$$

The proof of Theorem 3.3 is completed. □

4 Examples

Example 4.1 Consider the following singular IBVP

$$\{\begin{array}{c}{x}^{″}(t)-x(t)+\frac{\sqrt{t(1-t)}}{(e^{1+t}-e^{1-t})(e^{2-t}-e^t)}(\sqrt{t^2+1}|lnx|)=0,t\in (0,1)\setminus \{t_1\},\hfill \\ -\mathrm{△}{x}^{\prime }{|}_{t=t_1}=\sqrt[3]{x(t_1)},t_1=\frac{1}{2},\hfill \\ x(0)=\alpha [x],x(1)=\beta [x].\hfill \end{array}$$

(4.1)

We conclude that IBVP (4.1) has at least one positive solution.

Proof IBVP (4.1) can be regarded as a IBVP of the form (1.1), where $a(t)\equiv 0$, $b(t)\equiv -1$, $h(t)=\frac{\sqrt{t(1-t)}}{(e^{1+t}-e^{1-t})(e^{2-t}-e^t)}$, $f(t,u)=\sqrt{t^2+1}|lnu|$, $I_1(u)=\sqrt[3]{u}$. It is not difficult to see that $h(t)$ is singular at $t=0$ and $t=1$, $0<{\int }_0^{1}h(t)dt<+\mathrm{\infty }$, $h(t)\ge 0$ for $t\in (0,1)$, $f(t,u)\ge 0$, $I_1(u)\ge 0$ for $t\in J$, $u\in {\mathbb{R}}^{+}$. Choosing $\xi =\frac{1}{4}$, $\eta =\frac{3}{4}$, then

Let ϕ and ψ satisfy

Then

Case 1. Let $\alpha [x]=\frac{e^2-1}{2(e^{\frac{7}{4}}-e^{\frac{1}{4}})}x(\frac{1}{4})$, $\beta [x]=\frac{e^2-1}{2(e^{\frac{7}{4}}-e^{\frac{1}{4}})}x(\frac{3}{4})$. By direct calculation, we have

So all the conditions of Theorem 3.2 are satisfied. By Theorem 3.2, IBVP (4.1) has at least one positive solution.

Case 2. Let $\alpha [x]={\int }_0^{1}x(t)(4{\pi }^2+1)cos2\pi tdt$, that is $dA(t)=(4{\pi }^2+1)cos2\pi tdt$, so the measure dA changes sign on $[0,1]$. For convenience, we still take $\beta [x]=\frac{e^2-1}{2(e^{\frac{7}{4}}-e^{\frac{1}{4}})}x(\frac{3}{4})$. By direct calculation, we have

So all conditions of Theorem 3.2 are satisfied. By Theorem 3.2, IBVP (4.1) has at least one positive solution. □

Example 4.2 Consider the following singular IBVP

$$\{\begin{array}{c}{x}^{″}(t)+\frac{t}{1+t}{x}^{\prime }(t)-\frac{1}{1+t}x(t)+h(t)f(t,x(t))=0,t\in (0,1)\setminus \{t_1\},\hfill \\ -\mathrm{△}{x}^{\prime }{|}_{t=t_1}=I_1,t_1=\frac{1}{2},\hfill \\ x(0)=x(\frac{1}{2}),x(1)=\frac{1}{4}x(\frac{1}{2}),\hfill \end{array}$$

(4.2)

where

$$h(t)=\{\begin{array}{cc}\frac{1+t}{(2e^{-\frac{1}{2}}-e^{-1})t\sqrt{t}{e}^t},\hfill & 0\le t\le \frac{1}{2},\hfill \\ \frac{1+t}{(1-t{e}^{t-1})\sqrt{1-t}},\hfill & \frac{1}{2}\le t\le 1\hfill \end{array}$$

and

$$f(t,u)=\{\begin{array}{cc}\frac{1}{50}(t+1)(10-u),\hfill & 0\le t\le 1,0\le u\le 10,\hfill \\ \frac{1}{5}(t+1){(u-10)}^2,\hfill & 0\le t\le 1,10\le u\le 20,\hfill \\ \frac{1}{196}(t+1)(u+3900),\hfill & 0\le t\le 1,u\ge 20.\hfill \end{array}$$

We conclude that IBVP (4.2) has at least three positive solutions.

Proof IBVP (4.2) can be regarded as a IBVP of the form (1.1), where $a(t)=\frac{t}{1+t}$, $b(t)=-\frac{1}{1+t}$. It is not difficult to see that $h(t)$ is singular at $t=0$ and $t=1$, $0<{\int }_0^{1}h(t)dt<+\mathrm{\infty }$, $h(t)\ge 0$ for $t\in (0,1)$, $f(t,u)\ge 0$ for $t\in J$, $u\in {\mathbb{R}}^{+}$.

Let ϕ and ψ satisfy

Then

By direct calculation, we have

Therefore the conditions ($H_1$)-($H_3$) hold. In addition, $\sigma =\frac{12e+4-8\sqrt{e}}{7e+4-8\sqrt{e}}$, $\tau =\frac{7e-1+2\sqrt{e}}{7e+4-8\sqrt{e}}$,

Let $\xi =\frac{1}{8}$, $\eta =\frac{3}{4}$, $M=5$, $N=0$. Then $\gamma =\frac{1}{8}$, $\mathrm{\Gamma }>18.002$, $0<\mathrm{\Lambda }<0.715$. Take $\mathrm{\Gamma }=20$, $\mathrm{\Lambda }=\frac{1}{2}$, $a=10$, $b=20$, $c=1000$. Then $0<I_1\le 4.545$. Consequently, all the assumptions of Theorem 3.3 are satisfied, and thus, by Theorem 3.3, we infer that the singular IBVP (4.2) has at least three positive solutions $x_1$, $x_2$ and $x_3$ satisfying

 □