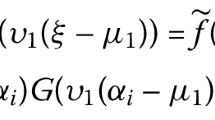Asymptotic behavior of impulsive non-autonomous delay difference equations with continuous variables

Abstract

In this article, a class of impulsive non-autonomous delay difference equations with continuous variables is considered. By establishing a delay difference inequality with impulsive initial conditions and using the decomposition approach, we obtain the attracting and invariant sets of the equations.

Introduction

Recently, there has been an increasing interest in the study of the asymptotic behavior and other behaviors of the difference equations with continuous variables in which the unknown function is a function of a continuous variable. In particular, delay effects on the asymptotic behavior and other behaviors of this kind of equations have widely been studied in the literature [1–7].

However, besides delay effects, impulsive effects likewise exist in a wide variety of evolutionary process, in which states are changed abruptly at certain moments of time. Recently, impulsive delay difference equations have extensively been studied by many authors. For example, the reader is referred to [8–13]. Unfortunately, impulsive delay difference equations with continuous variables are not well developed due to some theoretical and technical difficulties. Some sufficient conditions for the existence of the invariant and attracting sets of impulsive delay difference equations with continuous variables are obtained in [14, 15]. To the best of the authors' knowledge, there are no results on the corresponding problems for impulsive non-autonomous delay difference equations with continuous variables. With motivation from the above discussions, this article is devoted to the discussion of this problem. By establishing a delay difference inequality with impulsive initial conditions and using the decomposition approach, we obtain the attracting and invariant sets of the equations.

Preliminaries

Let ${ℝ}^n\left({ℝ}_{+}^n\right)$ be the space of n-dimensional (non-negative) real column vectors, ${ℝ}^{m\times n}\left({ℝ}_{+}^{m\times n}\right)$ be the set of m×n (non-negative) real matrices, E be the n-dimensional unit matrix, and |·| be the Euclidean norm of ℝⁿ. For A, B ∈ ℝ^m×nor A, B ∈ ℝⁿ, A ≥ B(A ≤ B, A > B, A < B) means that each pair of corresponding elements of A and B satisfies the inequality " ≥ (≤, >, <)". Especially, A is called a non-negative matrix if A ≥ 0, and z is called a positive vector if z > 0. $\mathcal{N}\triangleq \left\{1,2,\dots n\right\}$ and ϱ(A) denotes the spectral radius of A.

C[X, Y ] denotes the space of continuous mappings from the topological space X to the topological space Y. Especially, let C ≜ C[[-τ₂, 0], ℝⁿ], where τ₂ > 0.

$$PC\left[\mathbb{J},{ℝ}^n\right]=\left\{\psi :\mathbb{J}\to {ℝ}^n\left|\begin{array}{c}\psi \left(s\right)\text{is}\text{continuous}\text{for}\text{all}\text{but}\text{at}\text{most}\text{countable}\text{points}s\in \mathbb{J}\hfill \\ \text{and at these points }s\in \mathbb{J},\psi \left(s^{+}\right)\text{and}\psi \left(s^{-}\right)\text{exist},\psi \left(s\right)=\psi \left(s^{+}\right)\hfill \end{array}\right.\right\},$$

where $\mathbb{J}\subset ℝ$ is an interval, and ψ(s⁺) and ψ(s^-) denote the right- and left-hand limits of the the function ψ(s), respectively. Especially, let PC ≜ PC[[-τ₂, 0], ℝⁿ].

In this article, we consider the following impulsive non-autonomous delay difference equation with continuous variable

$$\{\begin{array}{l}{x}_i(t)=a_i(t)x_i(t-{\tau }_1)+{\displaystyle \sum _{j=1}^n{a}_{ij}}(t)f_j((x_j(t-{\tau }_2)),t\ne t_k,t\ge t_0,i\in \mathcal{N},\hfill \\ x_i(t)=J_{ik}(x_i(t^{-})),t\ge t_0,t=t_k,k=1,2,\dots ,i\in \mathcal{N},\hfill \\ x_i(t_0+\theta )={\varphi }_i(\theta ),{\varphi }_i\in PC[[-{\tau }_2,0],ℝ],\theta \in [-{\tau }_2,0],\hfill \end{array}$$

(1)

where a _i (t) = a _i h(t) and a _ij (t) = a _ij h(t), a _i and a _ij are real constants, h(t) ≤ 1 is a positive integral function and satisfies ${\mathsf{\text{sup}}}_{t\ge t_0}{\int }_{t-{\tau }_2}^{t}h\left(s\right)ds=H_2<\infty$ and ${\mathsf{\text{lim}}}_{t\to \infty }{\int }_{t_0}^{t}h\left(s\right)ds=\infty$. τ₁ and τ₂ are positive real numbers such that τ₁ < τ₂. t _k (k = 1, 2,...) is an impulsive sequence such that t₁ < t₂ <..., lim_k→∞t _k = ∞. f _j and J _ik : ℝ →ℝ are real-valued functions. Moreover, we assume that f _j (0) = 0 and J _ik (0) = 0, then system (1) admits an equilibrium solution x(t) ≡ 0.

By the solution of (1), we mean a piecewise continuous real-valued function x _i (t) defined on the interval [t₀ - τ₂, ∞) which satisfies (1) for all t ≥ t₀.

By the method of steps, one can easily see that, for any given initial function ϕ _i ∈ PC[[-τ₂, 0], ℝ], there exists a unique solution x _i (t), $i\in \mathcal{N}$, of (1).

For convenience, we rewrite the system (1) as the following vector form

$$\left\{\begin{array}{c}x\left(t\right)=h\left(t\right)\left[A_{0}x\left(t-{\tau }_1\right)+Af\left(x\left(t-{\tau }_2\right)\right)\right],t\ne t_k,t\ge t_0,\hfill \\ x\left(t\right)=J_k\left(x\left(t^{-}\right)\right),t\ge t_0,t=t_k,k=1,2,\dots ,\hfill \\ x\left(t_0+\theta \right)=\varphi \left(\theta \right),\theta \in \left[-{\tau }_2,0\right],\hfill \end{array}\right.$$

(2)

where x(t) = (x₁(t),..., x _n (t))^T , A₀ = diag{a₁,..., a _n }, A = (a _ij )_n×n, f(x) = (f₁(x₁),..., f _n (x _n ))^T, J _k (x) = (J_1k(x₁),..., J _nk (x _n ))^T , and ϕ = (ϕ₁,..., ϕ _n )^T ∈ PC.

Definition 2.1. The set S ⊂ PC is called a positive invariant set of (2), if for any initial value ϕ ∈ S, the solution x _t (t₀, ϕ) ∈ S, t ≥ t₀, where x _t (t₀, ϕ) = x(t + s, t₀, ϕ) ∈ PC, s ∈ [-τ₂, 0].

Definition 2.2. The set S ⊂ PC is called a global attracting set of (2), if for any initial value ϕ ∈ PC, the solution x(t, t₀, ϕ) satisfies

$$\mathsf{\text{dist}}\left(x\left(t,t_0,\varphi \right),S\right)\to 0,\mathsf{\text{as}}t\to +\infty ,$$

where dist(ϕ, S) = inf_ψ∈Sdist(ϕ, ψ), dist(ϕ, ψ) = sup_θ∈[-τ_2,0] |ϕ(θ) - ψ(θ)|, for ψ ∈ PC.

Definition 2.3. System (2) is said to be globally exponentially stable if for any solution x(t, t₀, ϕ), there exist constants λ₀ > 0 and κ₀ ≥ 0 such that,

$$\left|x\left(t,t_0,\varphi \right)\right|\le {\kappa }_0\left|\right|\varphi \left|\right|e^{-{\lambda }_0\left(t-t_0\right)},t\ge t_0,$$

where $\left|\right|\varnothing \left|\right|={\text{sup}}_{\theta \in [-{\tau }_2,0]}|\varnothing (s)|$.

Following [16], we split the matrices A₀, A into two parts, respectively,

$$A_0=A_0^{+}-A_0^{-},A=A^{+}-A^{-}$$

with $a_i^{+}=\mathsf{\text{max}}\left\{a_i,0\right\}$, $a_i^{-}=\mathsf{\text{max}}\left\{-a_i,0\right\}$, $a_{ij}^{+}=\mathsf{\text{max}}\left\{a_{ij},0\right\}$, $a_{ij}^{-}=\mathsf{\text{max}}\left\{-a_{ij},0\right\}$.

Set y = -x, g(u) = -f(-u). Then, by a similar argument with [15], we can get the following equations from the first equation of (2)

$$v\left(t\right)=h\left(t\right)\left[{\mathcal{A}}_{0}v\left(t-{\tau }_1\right)+\mathcal{A}\xi \left(v\left(t-{\tau }_2\right)\right)\right],$$

(3)

where

$$v(t)=\left\{\begin{array}{c}x(t)\\ y(t)\end{array}\right\},\xi (v(t))=\left\{\begin{array}{c}f(x(t))\\ g(y(t))\end{array}\right\},{\mathcal{A}}_0=\left\{\begin{array}{cc}{A}_0^{+}& A_0^{-}\\ A_0^{-}& A_0^{+}\end{array}\right\},\mathcal{A}=\left\{\begin{array}{cc}{A}^{+}& A^{-}\\ A^{-}& A^{+}\end{array}\right\}.$$

Set I _k (u) = -J _k (-u); in view of the impulsive part of (2), we have

$$v\left(t_k\right)={\omega }_k\left(v\left(t_k^{-}\right)\right),k=1,2,\dots ,$$

(4)

where ω _k (v) = (J _k (x)^T , I _k (y(t)^T)^T.

Lemma 2.1. [17, 18]If $M\in {ℝ}_{+}^{n\times n}$and ϱ(M) < 1, then (E - M) ^-1 ≥ 0.

Lemma 2.2. [18]Suppose that $M\in {ℝ}_{+}^{n\times n}$ and ϱ(M) < 1, then there exists a positive vector z such that (E - M) z > 0.

For $M\in {ℝ}_{+}^{n\times n}$ and ϱ(M) < 1, we denote

$${\mathrm{\Omega }}_{\varrho }\left(M\right)=\left\{z\in {ℝ}^n|\left(E-M\right)z>0,z>0\right\}.$$

In order to discuss the asymptotic behavior of (2), and for the brevity of later discussion, we list all our conditions as follows.

(A₁) For any x, y ∈ ℝⁿ , there exists a non-negative diagonal matrix $\bar{P}$ and vector μ = (μ₁,..., μ _n )^T ≥ 0 such that

$$f\left(x\right)-f\left(y\right)\le \bar{P}\left(x-y\right)+\mu .$$

(5)

(A₂) For any x, y ∈ ℝⁿ, there exist nonnegative matrices R _k such that

$$J_k\left(x\right)-J_k\left(y\right)\le R_k\left(x-y\right),k=1,2,\dots .$$

(6)

(A₃) Let $\varrho \left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)<1$, where $\mathcal{P}=\mathsf{\text{diag}}\left\{\bar{P},\bar{P}\right\}$.

(A₄) There exists a constant γ such that

$$\frac{\mathsf{\text{ln}}{\gamma }_k}{{\int }_{t_{k-\mathsf{\text{l}}}}^{t_k}h\left(s\right)ds}\le \gamma <\lambda ,k=1,2,\dots ,$$

(7)

where the scalar λ satisfies 0 < λ and is determined by the following inequality

$$\left({\mathcal{A}}_0{e}^{\lambda H_1}+\mathcal{A}\mathcal{P}{e}^{\lambda H_2}-E\right)z\le 0,$$

(8)

where $z={\left(z_1,\dots ,z_{2n}\right)}^T\in {\mathrm{\Omega }}_{\varrho }\left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)$, and

$${\gamma }_k\ge 1\mathsf{\text{and}}{\gamma }_{k}z\ge {\mathcal{R}}_{k}z,{\mathcal{R}}_k=\mathsf{\text{diag}}\left\{R_k,R_k\right\},k=1,2,\dots .$$

(9)

(A₅) Let

$$\sigma ={\displaystyle \sum _{k=1}^{\infty }\ln }{\sigma }_k<\infty ,k=1,2,\dots ,$$

(10)

where σ _k ≥ 1 satisfy

$${\mathcal{R}}_k{\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }\le {\sigma }_k{\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda },$$

(11)

where Λ = (μ^T, μ^T)^T.

Main results

In this section, we will give the main results of this article. The proofs of these results are placed in the following section for the sake of brevity.

Theorem 3.1. Let P = (p _ij )_n×n, $W={\left(w_{ij}\right)}_{n\times n}\in {ℝ}_{+}^{n\times n}$, $I={\left(I_1,\dots ,I_n\right)}^T\in {ℝ}_{+}^n$, and u(t) ∈ ℝⁿ be a solution of the following delay difference inequality with the initial condition u(t₀ + θ) = ϕ(θ), θ ∈ [-τ₂, 0] ϕ ∈ PC,

$$u\left(t\right)\le h\left(t\right)\left[Pu\left(t-{\tau }_1\right)+Wu\left(t-{\tau }_2\right)+I\right],t\ge t_0,$$

(12)

where τ₂ > τ₁, h(t) ≤ 1 is a positive integral function and ${\mathsf{\text{sup}}}_{t\ge t_0}{\int }_{t-{\tau }_2}^{t}h\left(s\right)ds=H_2<\infty$and ${\mathsf{\text{lim}}}_{t\to \infty }{\int }_{t_0}^{t}h\left(s\right)ds=\infty$.

If ϱ(P + W) < 1, then there exists a positive vector z = (z₁, z₂,..., z _n )^T such that

$$u\left(t\right)\le \kappa z{e}^{-\lambda {\int }_{t_0}^{t}h\left(s\right)ds}+{\left(E-P-W\right)}^{-1}I,t\ge t_0,$$

(13)

provided that the initial condition satisfies

$$u(t)\le \kappa z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}+{(E-P-W)}^{-1}I,\kappa \ge 0,t\in [t_0-{\tau }_2,t_0],$$

(14)

where the positive number λ > 0 is determined by the following inequality

$$\left(P{e}^{\lambda H_1}+W{e}^{\lambda H_2}-E\right)z\le 0,$$

(15)

where $H_1{\mathsf{\text{sup}}}_{t\ge t_0}{\int }_{t-{\tau }_1}^{t}h\left(s\right)ds$. Clearly, H₁ < H₂ < ∞.

Theorem 3.2. If (A₁)-(A₅) hold, then $S=\left\{\varphi \in PC|-e^{\sigma }{\mathcal{N}}_2\le \varphi \le e^{\sigma }{\mathcal{N}}_1\right\}$is a global attracting set of (2), where ${\mathcal{N}}_1,{\mathcal{N}}_2\in {ℝ}^n$ and ${\left({\mathcal{N}}_1^T,{\mathcal{N}}_2^T\right)}^T=\widehat{N}={\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }$.

Theorem 3.3. If (A₁)-(A₃) with R _k ≤ E hold, then $S=\left\{\varphi \in PC|-{\mathcal{N}}_2\le \varphi \le {\mathcal{N}}_1\right\}$is a positive invariant set and also a global attracting set of (2), where ${\mathcal{N}}_1,{\mathcal{N}}_2\in {ℝ}^n$ and ${\left({\mathcal{N}}_1^T,{\mathcal{N}}_2^T\right)}^T=\widehat{N}={\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }$

For the case I = 0, we easily observe x(t) ≡ 0 is a solution of (2) from (A₁) and (A₂). In the following, we give the attractivity of the zero solution and the proof is similar to that of Theorem 3.2.

Corollary 3.1. If (A₁)-(A₄) hold with I = 0, then the zero solution of (2) is globally exponentially stable.

Proofs of main results

Proof of Theorem 3.1. Since P, $W\in {ℝ}_{+}^{n\times n}$and ϱ(P + W) < 1, by Lemma 2.2, there exists a positive vector z ∈ Ω _ϱ (P + W) such that (E - P - W)) z > 0. By continuity, we know that (15) has at least one positive solution λ, i.e.,

$${\displaystyle \sum _{j=1}^n[p_{ij}{e}^{\lambda H_1}+w_{ij}{e}^{\lambda H_2}]}{z}_j\le z_i,i\in \mathcal{N}.$$

(16)

Set

$$u\left(t\right)=v\left(t\right)e^{-\lambda {\int }_{t_0}^{t}h\left(s\right)ds}+N,t\ge t_0-{\tau }_2,$$

(17)

where N = (E - P - W)^-1I; substituting (17) into (12), we have

$$v\left(t\right)e^{-\lambda {\int }_{t_0}^{t}h\left(s\right)ds}+N\le h\left(t\right)\left[P\left(v\left(t-{\tau }_1\right)e^{-\lambda {\int }_{t_0}^{t-{\tau }_1}h\left(s\right)ds}+N\right)+W\left(v\left(t-{\tau }_2\right)e^{-\lambda {\int }_{t_0}^{t-{\tau }_2}h\left(s\right)ds}+N\right)+I\right].$$

(18)

Then, by (18) and h(t) ≤ 1, we obtain

$$v\left(t\right)\le h\left(t\right)\left[Pv\left(t-{\tau }_1\right)e^{\lambda {\int }_{t-{\tau }_1}^{t}h\left(s\right)ds}+Wv\left(t-{\tau }_2\right)e^{\lambda {\int }_{t-{\tau }_2}^{t}h\left(s\right)ds}\right].$$

(19)

By (14) and (17), we get that

$$v\left(\theta \right)\le \kappa z,\theta \in \left[t_0-{\tau }_2,t_0\right].$$

(20)

Next, we will prove for any t ≥ t₀,

$$v\left(t\right)\le \kappa z.$$

(21)

To prove (21), we first prove that for any positive constant ε,

$$v\left(t\right)<\left(1+\epsilon \right)\kappa z,t\ge t_0.$$

(22)

If (22) is not true, then there must be a t* > t₀ and some integer r such that

$$v\left(t\right)<\left(1+\epsilon \right)\kappa z,\mathsf{\text{for}}t\in \left[t_0,t^{*}\right),v_r\left(t^{*}\right)=\left(1+\epsilon \right)\kappa z_r.$$

(23)

By using (16) and (19), we obtain that

$$\begin{array}{l}(1+\epsilon )\kappa z_r=v_r(t^{*})\le h(t^{*}){\displaystyle \sum _{j=1}^n[p_{rj}{v}_j(t^{*}-{\tau }_1)e^{\lambda {\displaystyle {\int }_{t^{*}-{\tau }_1}^{t^{*}}h}(s)ds}+w_{rj}{v}_j(t^{*}-{\tau }_2)e^{\lambda {\displaystyle {\int }_{t^{*}-{\tau }_2}^{t^{*}}h}(s)ds}]}\\ <h(t^{*}){\displaystyle \sum _{j=1}^n[p_{rj}}{e}^{\lambda {\displaystyle {\int }_{t^{*}-{\tau }_1}^{t^{*}}h}(s)ds}+w_{rj}{e}^{\lambda {\displaystyle {\int }_{t^{*}-{\tau }_2}^{t^{*}}h}(s)ds}](1+\epsilon )\kappa z_j\\ \le h(t^{*}){\displaystyle \sum _{j=1}^n[p_{rj}{e}^{\lambda H_1}+w_{rj}{e}^{\lambda H_2}]}(1+\epsilon )\kappa z_j\\ \le (1+\epsilon )\kappa z_r\end{array}$$

which is a contradiction. Hence, (22) holds for all numbers ε > 0; it follows immediately that (21) is always satisfied, which can easily be led to (13). This completes the proof.    □

Proof of Theorem 3.2. Since $\varrho \left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)<1$, by Lemma 2.2, there exists a positive vector $z\in {\mathrm{\Omega }}_{\varrho }\left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)$ such that $\left(E-\left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)\right)z>0$. Using continuity, we obtain that inequality (8) has at least one positive solution λ.

From (5) and Condition (6), we can claim that for any v ∈ℝ²ⁿ,

$$\xi \left(v\right)\le \mathcal{P}v+\mathrm{\Lambda },$$

(24)

and

$${\omega }_k\left(v\right)\le {\mathcal{R}}_{k}v\left(t_k^{-}\right),k=1,2,\dots ,$$

(25)

where Λ = (μ^T, μ^T)^T.

So by using (3) and (4) and taking into account (24) and (25), we get

$$v\left(t\right)\le h\left(t\right)\left[{\mathcal{A}}_{0}v\left(t-{\tau }_1\right)+\mathcal{A}\mathcal{P}v\left(t-{\tau }_2\right)+\mathcal{A}\mathrm{\Lambda }\right],$$

(26)

and

$$v\left(t_k\right)\le {\mathcal{R}}_{k}v\left(t_k^{-}\right),k=1,2,\dots ,$$

(27)

respectively.

Noting $\varrho \left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)<1$ and ${\mathcal{A}}_0$, $\mathcal{A}\mathcal{P}\in {ℝ}_{+}^{n\times n}$, then, by Lemma 2.1, we can get ${\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\ge 0$ and $\widehat{N}\triangleq {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }\ge 0$.

For the initial conditions: x(t₀ + θ) = ϕ(θ), θ ∈ [-τ₂, 0], where ϕ ∈ PC, we have

$$v(t)\le {\kappa }_{0}z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}\le {\kappa }_{0}z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}+\widehat{N},t\in [t_0-{\tau }_2,t_0],$$

(28)

where

$${\kappa }_0=\frac{\left|\right|\varphi \left|\right|}{{\mathsf{\text{min}}}_{1\le i\le 2n}\left\{z_i\right\}},z\in {\mathrm{\Omega }}_{\varrho }\left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right).$$

Then, all the conditions of Theorem 3.1 are satisfied by (26), (28), and Condition (A₃), we derive that

$$v\left(t\right)\le {\kappa }_{0}z{e}^{-\lambda {\int }_{t_0}^{t}h\left(s\right)ds}+\widehat{N},t\in \left[t_0,t_1\right).$$

(29)

Suppose for all ι = 1,..., k, the inequalities

$$v(t)\le {\gamma }_0\cdots {\gamma }_{\iota -1}{\kappa }_{0}z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}+{\sigma }_0\cdots {\sigma }_{\iota -1}\widehat{N},t\in [t_{\iota -1},t_{\iota }),$$

(30)

hold, where γ₀ = σ₀ = 1. Then, from (9), (11), (30), and (A₂), the impulsive part of (2) satisfies that

$$\begin{array}{cc}\hfill v\left(t_k\right)& \le {\mathcal{R}}_{k}v\left(t_k^{-}\right)\hfill \\ \le {\mathcal{R}}_k\left[{\gamma }_0\cdots {\gamma }_{k-1}{\kappa }_{0}z{e}^{-\lambda {\int }_{t_0}^{t_k}h\left(s\right)ds}+{\sigma }_0\cdots {\sigma }_{k-1}\widehat{N}\right]\hfill \\ \le {\gamma }_0\cdots {\gamma }_{k-1}{\gamma }_k{\kappa }_{0}z{e}^{-\lambda {\int }_{t_0}^{t_k}h\left(s\right)ds}+{\sigma }_0\cdots {\sigma }_{k-1}{\sigma }_k\widehat{N}.\hfill \end{array}$$

(31)

This, together with (30) and γ _k , σ _k ≥ 1, leads to

$$v(t)\le {\gamma }_0\cdots {\gamma }_{k-1}{\gamma }_k{\kappa }_{0}z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}+{\sigma }_0\cdots {\sigma }_{k-1}{\sigma }_k\widehat{N},t\in [t_k-{\tau }_2,t_k].$$

(32)

On the other hand,

$$v(t)\le h(t)[{\mathcal{A}}_{0}v(t-{\tau }_1)+\mathcal{A}\mathcal{P}v(t-{\tau }_2)+{\sigma }_0,\cdots {\sigma }_k\mathcal{A}\Lambda ],t\ne t_k.$$

(33)

It follows from (32)-(33) and Theorem 3.1 that

$$v(t)\le {\gamma }_0\cdots {\gamma }_{k-1}{\gamma }_k{\kappa }_{0}z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}+{\sigma }_0\cdots {\sigma }_{k-1}{\sigma }_k\widehat{N},t\in [t_k,t_{k+1}).$$

(34)

By the mathematical induction, we can conclude that

$$v(t)\le {\gamma }_0\cdots {\gamma }_{k-1}{\kappa }_{0}z{e}^{-\lambda {\displaystyle {\int }_{t_0}^{t}h}(s)ds}+{\sigma }_0\cdots {\sigma }_{k-1}\widehat{N},t\in [t_{k-1},t_k),k=1,2,\dots .$$

(35)

From (7) and (10),

$${\gamma }_k\le e^{\gamma {\int }_{t_{k-1}}^{t_k}h\left(s\right)ds},{\sigma }_0\cdots {\sigma }_{k-1}\le e^{\sigma },$$

we can use (35) to conclude that

$$\begin{array}{cc}\hfill v\left(t\right)& \le e^{\gamma {\int }_{t_0}^{t_1}h\left(s\right)ds}\cdots e^{\gamma {\int }_{t_{k-2}}^{t_{k-1}}h\left(s\right)ds}{\kappa }_{0}z{e}^{-\lambda {\int }_{t_0}^{t}h\left(s\right)ds}+{\sigma }_0\cdots {\sigma }_{k-1}\widehat{N}\hfill \\ \le {\kappa }_{0}z{e}^{\gamma {\int }_{t_0}^{t}h\left(s\right)ds}{e}^{-\lambda {\int }_{t_0}^{t}h\left(s\right)ds}+e^{\sigma }\widehat{N}\hfill \\ ={\kappa }_{0}z{e}^{-\left(\lambda -\gamma \right){\int }_{t_0}^{t}h\left(s\right)ds}+e^{\sigma }\widehat{N},t\in \left[t_{k-1},t_k\right),k=1,2,\dots .\hfill \end{array}$$

This implies that the conclusion of the theorem holds and the proof is complete.    □

Proof of Theorem 3.3. Similarly, the inequality (8) holds by (A₃). For the initial conditions: x(t₀ + s) = ϕ(s), s ∈ [-τ₂, 0], where ϕ ∈S, we have

$$v\left(t\right)\le {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda },t\in \left[t_0-{\tau }_2,t_0\right].$$

(36)

By (36) and Theorem 3.1 with κ = 0, we have

$$v\left(t\right)\le {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda },t\in \left[t_0,t_1\right).$$

(37)

Then, from (27) and R _k ≤ E,

$$v\left(t_1\right)\le {\mathcal{R}}_{1}v\left(t_1^{-}\right)\le Ev\left(t_1^{-}\right)\le {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }.$$

(38)

Thus,

$$v\left(t\right)\le {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda },t\in \left[t_1-{\tau }_2,t_1\right].$$

(39)

Using Theorem 3.1 again, we obtain

$$v\left(t\right)\le {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda },t\in \left[t_1,t_2\right).$$

(40)

By introduction, we have

$$v\left(t\right)\le {\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda },t\in \left[t_{k-1},t_k\right),k=1,2,\dots .$$

(41)

Therefore, $S=\left\{\varphi \in PC|-{\mathcal{N}}_2\le \varphi \le {\mathcal{N}}_1\right\}$is a positive invariant set. Since ℛ _k ≤ E, a direct calculation shows that γ _k = σ _k = 1 and σ = 0 in Theorem 3.2. It follows from Theorem 3.2 that the set S is also a global attracting set of (2). The proof is complete.    □

Illustrative example

The following illustrative example will demonstrate the effectiveness of our results.

Example 4.1 Consider the following impulsive delay difference equation:

$$\left\{\begin{array}{c}{x}_1\left(t\right)=\left(1+{\mathsf{\text{cos}}}^{2}t\right)\left[\frac{1}{4}{x}_1\left(t-1\right)+\frac{1}{3}{x}_2\left(t-2\right)+2\right]\hfill \\ x_2\left(t\right)=\left(1+{\mathsf{\text{cos}}}^{2}t\right)\left[-\frac{1}{4}{x}_2\left(t-1\right)+\frac{1}{5}{x}_1\left(t-2\right)+2\right]\hfill \end{array}\right.,t\ne t_k,$$

(42)

with

$$\left\{\begin{array}{c}{x}_1\left(t_k\right)={\alpha }_{1k}{x}_1\left(t_k^{-}\right)-{\beta }_{1k}{x}_2\left(t_k^{-}\right)\hfill \\ x_2\left(t_k\right)={\beta }_{2k}{x}_1\left(t_k^{-}\right)+{\alpha }_{2k}{x}_2\left(t_k^{-}\right)\hfill \end{array}\right.,$$

where α _ik and β _ik are non-negative constants, and the impulsive sequence t _k (k = 1, 2,...) satisfy: t₁ < t₂ < · · · , lim_k→∞t _k = ∞.

The parameters of (A₁)-(A₃) are as follows:

$$\begin{array}{c}{A}_0=\left(\begin{array}{c}\hfill \frac{1}{4}0\hfill \\ \hfill 0-\frac{1}{4}\hfill \end{array}\right),A=\left(\begin{array}{c}\hfill 0\frac{1}{3}\hfill \\ \hfill \frac{1}{5}0\hfill \end{array}\right),\bar{P}=\left(\begin{array}{c}\hfill 10\hfill \\ \hfill 01\hfill \end{array}\right),\mu =\left(\begin{array}{c}\hfill 2\hfill \\ \hfill 2\hfill \end{array}\right),R_k=\left(\begin{array}{cc}\hfill {\alpha }_{1k}\hfill & \hfill {\beta }_{1k}\hfill \\ \hfill {\beta }_{2k}\hfill & \hfill {\alpha }_{2k}\hfill \end{array}\right),\\ {\mathcal{A}}_0=\left(\begin{array}{c}\hfill \frac{1}{4}000\hfill \\ \hfill 000\frac{1}{4}\hfill \\ \hfill 00\frac{1}{4}0\hfill \\ \hfill 0\frac{1}{4}00\hfill \end{array}\right),\mathcal{A}=\left(\begin{array}{c}\hfill 0\frac{1}{3}00\hfill \\ \hfill \frac{1}{5}000\hfill \\ \hfill 000\frac{1}{3}\hfill \\ \hfill 00\frac{1}{5}0\hfill \end{array}\right),{\mathcal{R}}_k=\left(\begin{array}{cccc}\hfill {\alpha }_{1k}\hfill & \hfill {\beta }_{1k}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\beta }_{2k}\hfill & \hfill {\alpha }_{2k}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\alpha }_{1k}\hfill & \hfill {\beta }_{1k}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\beta }_{2k}\hfill & \hfill {\alpha }_{2k}\hfill \end{array}\right),\end{array}$$

and $\mathcal{P}=\mathsf{\text{diag{ 1,1,1,1}}}$.

It is easy to prove that $\varrho \left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)=0.5082<1$ and

$${\mathrm{\Omega }}_{\varrho }\left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)=\left\{{\left(z_1,z_2,z_3,z_4\right)}^T>0\left|\left\{\begin{array}{c}\frac{3}{4}{z}_1-\frac{1}{3}{z}_2>0\hfill \\ -\frac{1}{5}{z}_1+z_2-\frac{1}{4}{z}_4>0\hfill \\ \frac{3}{4}{z}_3-\frac{1}{3}{z}_4>0\hfill \\ -\frac{1}{4}{z}_2-\frac{1}{5}{z}_3+z_4>0\hfill \end{array}\right\}\right.\right..$$

Let $z={\left(1,1,1,1\right)}^T\in {\mathrm{\Omega }}_{\varrho }\left({\mathcal{A}}_0+\mathcal{A}\mathcal{P}\right)$and λ = 0.05 which satisfies the inequality

$$\left({\mathcal{A}}_0{e}^{\lambda H_1}+\mathcal{A}{\mathcal{P}}^{\lambda H_2}-E\right)z\le 0,$$

where, $1\le H_1={\int }_{t-1}^t\left(1+{\mathsf{\text{cos}}}^{2}t\right)ds\le 2$, $2\le H_2={\int }_{t-2}^t\left(1+{\mathsf{\text{cos}}}^{2}t\right)ds\le 4$.

Let γ _k = 3 max{α_1k+ β_1k, α_2k+ β_2k}, then γ _k satisfy γ _k z ≥ R _k z, k = 1, 2,....

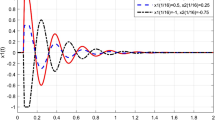
Case 4.1. Let ${\alpha }_{1k}={\alpha }_{2k}=\frac{1}{9}{e}^{\frac{1}{{25}^k}}$, ${\beta }_{1k}={\beta }_{2k}=\frac{2}{9}{e}^{\frac{1}{{25}^k}}$ and t _k - t_k-1= 2k, then ${\gamma }_k=e^{\frac{1}{{25}^k}}\ge 1$ and

$$\frac{\mathsf{\text{ln}}{\gamma }_k}{{\int }_{t_{k-\mathsf{\text{l}}}}^{t_k}h\left(s\right)ds}=\frac{\mathsf{\text{ln}}{\gamma }_k}{{\int }_{t_{k-1}}^{t_k}\left(1+{\mathsf{\text{cos}}}^{2}t\right)ds}\le \frac{\mathsf{\text{ln}}{e}^{\frac{1}{{25}^k}}}{2k}=\frac{1}{{25}^k\times 2k}\le 0.02=\gamma <\lambda .$$

By simple computation, we know that ${\sigma }_k=e^{\frac{1}{{25}^k}}\ge 1$, $\sigma ={\sum }_{k=1}^{\infty }\mathsf{\text{ln}}{\sigma }_k={\sum }_{k=1}^{\infty }\mathsf{\text{ln}}{e}^{\frac{1}{{25}^k}}=\frac{1}{24}$, ${\mathcal{R}}_k{\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }=e^{\frac{1}{{25}^k}}{\left(0.3361,0.3810,0.3361,0.3810\right)}^T$, ${\sigma }_k{\left(E-{\mathcal{A}}_0-\mathcal{A}\mathcal{P}\right)}^{-1}\mathcal{A}\mathrm{\Lambda }=e^{\frac{1}{{25}^k}}{\left(1.2773,0.8739,1.2773,0.8739\right)}^T$.

Clearly, all conditions of Theorem 3.2 are satisfied. So $S=\{\varphi \in PC|-{(1.2773e^{\frac{1}{24}},0.8739e^{\frac{1}{24}})}^T\le \varphi \le {(1.2773e^{\frac{1}{24}},0.8739e^{\frac{1}{24}})}^T$ is a global attracting set of (42).

Case 4.2. Let ${\alpha }_{1k}={\alpha }_{2k}=\frac{1}{9}{e}^{\frac{1}{2^k}}$ and β_1k= β_2k= 0, then $R_k=\frac{1}{9}{e}^{\frac{1}{2^k}}E\le E$. Therefore, by Theorem 3.3, S = {ϕ ∈ PC| - (1.2773, 0.8739)^T ≤ ϕ ≤ (1.2773, 0.8739)^T is a positive invariant set and also a global attracting set of (42).

Case 4.3. If μ = 0 and let ${\alpha }_{1k}={\alpha }_{2k}=\frac{1}{3}{e}^{0.04k}$ and ${\beta }_{1k}={\beta }_{2k}=\frac{2}{3}{e}^{0.04k}$, then γ _k = e^0.04k≥ 1 and

$$\frac{\mathsf{\text{ln}}{\gamma }_k}{{\int }_{t_{k-\mathsf{\text{l}}}}^{t_k}h\left(s\right)ds}=\frac{\mathsf{\text{ln}}{\gamma }_k}{{\int }_{t_{k-1}}^{t_k}\left(1+{\mathsf{\text{cos}}}^{2}t\right)ds}\le \frac{\mathsf{\text{ln}}{e}^{0.04k}}{2k}=0.02=\gamma <\lambda .$$

Clearly, all conditions of Corollary 3.1 are satisfied. Therefore, by Corollary 3.1, the zero solution of (42) is globally exponentially stable.