Periodic solutions for a class of higher-order difference equations

Abstract

In this article, we discuss the existence of periodic solutions for the higher-order difference equation

$$x(n+k)=g(x(n))-f(n,x(n-\tau (n)).$$

We show the existence of periodic solutions by using Schauder's fixed point theorem, and illustrate three examples.

MSC 2010: 39A10; 39A12.

1 Introduction and main results

Let ℝ denote the set of the real numbers, ℤ the integers and ℕ the positive integers. In this article, we investigate the existence of periodic solutions of the following high-order functional difference equation

$$x(n+k)=g(x\left(n\right))-f(n,x(n-\tau (n\left)\right),n\in \mathbb{Z},$$

(1.1)

where k ∈ N, τ : ℤ → ℤ and τ (n + ω) = τ (n), f (n + ω, u) = f (n, u) for any (n, u) ∈ ℤ × ℝ, ω ∈ ℕ.

Difference equations have attracted the interest of many researchers in the last 20 years since they provided a natural description of several discrete models, in which the periodic solution problem is always a important topic, and the reader can consult [1–7] and the references therein. There are many good results about existence of periodic solutions for first-order functional difference equations [8–12]. Only a few article have been published on the same problem for higher-order functional difference equations. Recently, using coincidence degree theory, Liu [13] studied the second-order nonlinear functional difference equation

$${\Delta }^{2}x\left(n-1\right)=f\left(n,x\left(n-{\tau }_1\left(n\right)\right),x\left(n-{\tau }_2\left(n\right)\right),\dots ,x\left(n-{\tau }_m\left(n\right)\right)\right),$$

(1.2)

and obtain sufficient conditions for the existence of at least one periodic solution of equation (1.2). By using fixed point theorem in a cone, Wang and Chen [14] discussed the following higher-order functional difference equation

$$x\left(n+m+k\right)-ax\left(n+m\right)-bx\left(n+k\right)+abx\left(n\right)=f\left(n,x\left(n-\tau \left(n\right)\right)\right),$$

(1.3)

where a ≠ 1, b ≠ 1 are positive constants, τ : ℤ → ℤ and τ(n+ω) = τ(n), ω, m, k ∈ ℕ, and obtained existence theorem for single and multiple positive periodic solutions of (1.3).

Our aim of this article is to study the existence of periodic solutions for the higher-order difference equations (1.1) using the well-known Schauder's fixed point theorem. Our results extend the known results in the literature.

The main results of this article are following sufficient conditions which guarantee the existence of a periodic solution for (1.1).

Theorem 1.1. Assume that there exist constants m < M, r > 0 such that g ∈ C ¹[m, M] with r ≤ g'(u) ≤ 1 for any u ∈ [m, M] and f (n, u): ℤ × [m, M] → ℝ is continuous in u,

$$g\left(M\right)-M\le f\left(n,u\right)\le g\left(m\right)-m$$

(1.4)

for any (n, u) ∈ ℤ × [m, M], then (1.1) has at least one ω-periodic solution x with m ≤ x ≤ M.

Theorem 1.2. Assume that there exist constants m < M such that g ∈ C ¹[m, M] with g'(u) ≥ 1 for any u ∈ [m, M] and f (n, u): ℤ × [m, M] → ℝ is continuous in u,

$$g\left(m\right)-m\le f\left(n,u\right)\le g\left(M\right)-M$$

(1.5)

for any (n, u) ∈ ℤ × [m, M], then (1.1) has at least one ω-periodic solution x with m ≤ x ≤ M.

2 Some examples

In this section, we present three examples to illustrate our conclusions.

Example 2.1. Consider the difference equation

$$x\left(n+k\right)=ax\left(n\right)+q\left(n\right)\sqrt[3]{x\left(n-\tau \left(n\right)\right)},$$

(2.1)

$$x\left(n+k\right)=bx\left(n\right)-q\left(n\right)\sqrt[3]{x\left(n-\tau \left(n\right)\right)},$$

(2.2)

where k ∈ ℕ, 0 < a < 1, b > 1, q is one ω-periodic function with q(n) > 0 for all n ∈ [1, ω] and τ : ℤ → ℤ and τ (n + ω) = τ (n).

Let m > 0 be sufficiently small and M > 0 sufficiently large. It is easy to check that

$$\begin{array}{c}\left(a-1\right)M\le -q\left(n\right)\sqrt[3]{u}\le \left(a-1\right)m,\\ \left(b-1\right)m\le q\left(n\right)\sqrt[3]{u}\le \left(b-1\right)M\end{array}$$

for n ∈ ℤ and u ∈ [m.M]. By Theorem 1.1 (Theorem 1.2), Equation (2.1) (or (2.2)) has at least one positive ω-periodic solution x with m ≤ x ≤ M. When k = 1, this conclusion about (2.1) and (2.2) can been obtained from the results in [15]. Our result holds for all k ∈ ℕ.

Remark 1 Consider the difference equations

$$x\left(n+k\right)=ax\left(n\right)+q\left(n\right)f\left(x\left(n-\tau \left(n\right)\right)\right),$$

(2.3)

$$x\left(n+k\right)=bx\left(n\right)-q\left(n\right)f\left(x\left(n-\tau \left(n\right)\right)\right),$$

(2.4)

where k ∈ ℕ, 0 < a < 1, b > 1, q is one ω-periodic function with q(n) > 0 for all n ∈ [1, ω], τ : ℤ → ℤ and τ(n + ω) = τ (n) and f : (0, + ∞) → (0, + ∞) is continuous.

The following result generalizes the conclusion of Example 2.1.

Proposition 2.1 Assume that f ₀ = + ∞ and f _∞, = 0, here

$$f_0=\underset{u\to 0+}{lim}\frac{f\left(u\right)}{u},f_{\infty }=\underset{u\to \infty }{lim}\frac{f\left(u\right)}{u},$$

then (2.3) or (2.4) has at least one positive ω-periodic solution.

Proof Here, we only consider (2.3). From f ₀ = + ∞ and f _∞ = 0, we obtain that there exist 0 < ρ ₁ < ρ ₂ such that

$$f\left(u\right)\ge \frac{1-a}{minq\left(n\right)}u,0<u\le {\rho }_1,f\left(u\right)\le \frac{1-a}{maxq\left(n\right)}u,u\ge {\rho }_2.$$

Let A = min q(n) min {f (u): ρ ₁ ≤ u ≤ ρ ₂} and B = max q(n) max{f (u): ρ ₁ ≤ u ≤ ρ ₂}. Choosing θ ∈ (0, 1) such that

$$\frac{A}{1-a}\ge \theta {\rho }_1,\frac{B}{1-a}\le {\theta }^{-1}{\rho }_2,$$

we obtain that

$$\begin{array}{c}f\left(u\right)\ge \frac{1-a}{minq\left(n\right)}u\ge \frac{\theta \left(1-a\right){\rho }_1}{minq\left(n\right)},\theta {\rho }_1\le u\le {\rho }_1,\\ f\left(u\right)\le \frac{{\theta }^{-1}\left(1-a\right){\rho }_2}{maxq\left(n\right)},{\rho }_2\le u\le {\theta }^{-1}{\rho }_2,\\ A\le q\left(n\right)f\left(u\right)\le B,\forall n\in \mathbb{Z},{\rho }_1\le u\le {\rho }_2.\end{array}$$

Using the above three inequalities, we have

$$\left(1-a\right)\theta {\rho }_1\le q\left(n\right)f\left(u\right)\le \left(1-a\right){\theta }^{-1}{\rho }_2,\forall n\in \mathbb{Z},\theta {\rho }_1\le u\le {\theta }^{-1}{\rho }_2.$$

By Theorem 1.1, Equation (2.3) has at least one positive ω-periodic solution x with θ ρ ₁ ≤ x ≤ θ ^-1 ρ ₂. □

Example 2.2. Consider the difference equation

$$x\left(n+k\right)=-\frac{1}{x^{\alpha }\left(n\right)}+q\left(n\right),$$

(2.5)

where k ∈ ℕ, α > 0, q is one ω-periodic function.

We claim that there is a λ > 0 such that (2.5) has at least two positive ω-periodic solutions for min q(n) > λ.

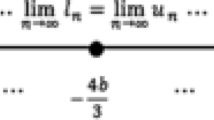
In fact, g(x) = - x ^-α. Let $0<a<\sqrt[\alpha +1]{\alpha }$ be sufficiently small and $b>\sqrt[\alpha +1]{\alpha }$ be sufficiently large, then

$$\begin{array}{c}\frac{\alpha }{b^{\alpha +1}}\le g^{\prime }\left(x\right)=\frac{\alpha }{x^{\alpha +1}}\le 1,\mathsf{\text{for}}x\in \left[\sqrt[\alpha +1]{\alpha },b\right],\\ g^{\prime }\left(x\right)=\frac{\alpha }{x^{\alpha +1}}\ge 1,\mathsf{\text{for}}x\in \left[a,\sqrt[\alpha +1]{\alpha }\right].\end{array}$$

If the following conditions are fulfilled

$$-\frac{1}{b^{\alpha }}-b\le -q\left(n\right)\le -\frac{1}{\sqrt[\alpha +1]{{\alpha }^{\alpha }}}-\sqrt[\alpha +1]{\alpha },\forall n\in \mathbb{Z},$$

(2.6)

$$-\frac{1}{a^{\alpha }}-a\le -q\left(n\right)\le -\frac{1}{\sqrt[\alpha +1]{{\alpha }^{\alpha }}}-\sqrt[\alpha +1]{\alpha },\forall n\in \mathbb{Z},$$

(2.7)

then (2.5) has at least one periodic solution $\left[a,\sqrt[\alpha +1]{\alpha }\right]$ and $\left[\sqrt[\alpha +1]{\alpha },b\right]$ respectively. When min q(n) is sufficiently large, the conditions (2.6) and (2.7) are satisfied.

Example 2.3. Consider the difference equation

$$x\left(n+k\right)=x^3\left(n\right)-2x\left(n\right)-q\left(n\right)x^2\left(n-\tau \left(n\right)\right),$$

(2.8)

where k ∈ ℕ, q is one ω-periodic function with q(n) > 0 for all n ∈ [1, ω], τ : ℤ → ℤ and τ (n + ω) = τ (n).

Let m = 1, M > 3 + max q(n) and g(u) = u ³ - 2u, f (n, u) = q(n)u ². It is easy to check that g'(u) ≥ 1 for u ∈ [m, M], and

$$g\left(m\right)-m=-2<f\left(n,u\right)\le g\left(M\right)-M=M^3-3M,\forall n\in \mathbb{Z},u\in \left[m,M\right].$$

By Theorem 1.2, Equation (2.8) has at least one positive ω-periodic solution x with m ≤ x ≤ M.

Remark 2 Consider the difference equation

$$x\left(n+k\right)=g\left(x\left(n\right)\right)-q\left(n\right)f\left(x\left(n-\tau \left(n\right)\right)\right),$$

(2.9)

where k ∈ ℕ, q is one ω-periodic function with q(n) > 0 for all n ∈ [1, ω], τ : ' → ' and τ(n + ω) = τ(n) and f : (0, +∞) → (0, +∞) is continuous.

Proposition 2.2 Assume that there exists a > 0 such that g ∈ C ¹([a, +∞), R) with g'(u) ≥ 1 for u > a, f(u) ≥ (g(a) - a)/min q(n) for u ≥ a. Further suppose that

$$\underset{u\to +\infty }{lim}\frac{g\left(u\right)-u}{f\left(u\right)}>maxq\left(n\right),\underset{u\to +\infty }{lim}\left(g\left(u\right)-u\right)=+\infty .$$

Then (2.9) has at least one positive ω-periodic solution.

Proof There exist ρ > 0 such that

$$g\left(u\right)-u\ge f\left(u\right)maxq\left(n\right),u\ge \rho .$$

Let A = min q(n) min{f(u): a ≤ u ≤ ρ} and B = max q(n) max{f(u): a ≤ u ≤ ρ}. Since lim _u→+∞(g(u) - u) = +∞ and g'(u) ≥ 1 for u > a, there is M > ρ such that g(M) - M > B and

$$f\left(u\right)maxq\left(n\right)\le g\left(u\right)-u\le g\left(M\right)-M,\rho \le u\le M.$$

Thus, (2.9) has at least one ω-periodic solution x with a ≤ x ≤ M. □

3 Proof

Let X be the set of all real ω-periodic sequences. When endowed with the maximum norm ||x|| = max _{n∈[0, ω-1]}|x(n)|, X is a Banach space.

Let k ∈ ℕ and 0 < c ≠ 1, and consider the equation

$$x\left(n+k\right)=cx\left(n\right)+\gamma \left(n\right),$$

(3.1)

where γ ∈ X. Set (k, ω) is the greatest common divisor of k and ω, h = ω/(k, ω). We obtain that if x ∈ X satisfies (3.1), then

$$\begin{array}{c}{c}^{-1}x\left(n+k\right)-x\left(n\right)=c^{-1}\gamma \left(n\right),\\ c^{-2}x\left(n+2k\right)-c^{-1}x\left(n+k\right)=c^{-2}\gamma \left(n+k\right),\\ \cdots \cdots \cdots \cdots \\ c^{-p}x\left(n+hk\right)-c^{1-p}x\left(n+\left(h-1\right)k\right)=c^{-p}\gamma \left(n+\left(h-1\right)k\right).\end{array}$$

By summing the above equations and using periodicity of x, we obtain the following result.

Lemma 3.1. Assume that 0 < c ≠ 1, then (3.1) has a unique periodic solution

$$x\left(n\right)={\left(c^{-h}-1\right)}^{-1}\sum _{i=1}^h{c}^{-i}\gamma \left(n+\left(i-1\right)k\right).$$

The following well-known Schauder's fixed point theorem is crucial in our arguments.

Lemma 3.2. [16]Let X be a Banach space with D ⊂ X closed and convex. Assume that T : D → D is a completely continuous map, then T has a fixed point in D.

Now, we rewrite (1.1) as

$$x(n+k)=px\left(n\right)+\left[g\right(x\left(n\right))-f(n,x(n-\tau (n\left)\right)-px\left(n\right)],$$

(3.2)

where p > 0 is a constant which is determined later. By Lemma 3.1, if x is a periodic solution of (1.1), x satisfies

$$x\left(n\right)={\left(p^{-h}-1\right)}^{-1}\sum _{i=1}^h{p}^{-i}\left(H_{p}x\right)\left(n+\left(i-1\right)k\right),$$

where h = ω/(k, ω), the mapping H _p is defined as

$$\left(H_{p}x\right)\left(n\right)=g\left(x\right(n\left)\right)-px\left(n\right)-f(n,x(n-\tau \left(n\right)),x\in X.$$

Define a mapping T _p in X by

$$\left(T_{p}x\right)\left(n\right)={\left(p^{-h}-1\right)}^{-1}\sum _{i=1}^h{p}^{-i}\left(H_{p}x\right)\left(n+\left(i-1\right)k\right),x\in X.$$

Clearly, the fixed point of T _p in X is a periodic solution of (1.1).

Proof of Theorem 1.1 Let p = r and Ω = {x ∈ X : m ≤ x(n) ≤ M for n ∈ '}, then Ω is a closed and convex set. If r = 1, then g(u) = u on [m, M]. It is easy to check that any constant c ∈ [m, M] is a periodic solution of (1.1). Set r < 1. Now we show that T _r satisfies all conditions of Lemma 3.2. Noting that the function g(u) - ru is nondecreasing in [m, M], we have for any x ∈ Ω,

$$g\left(m\right)-rm\le g\left(x\left(n\right)\right)-rx\left(n\right)\le g\left(M\right)-rM,\forall n\in \mathbb{Z}.$$

Let (1.4) be fulfilled. For any x ∈ Ω and n ∈ ℤ,

$$\begin{array}{c}(H_{r}x)(n)=g(x(n))-px(n)-f(n,x(n-\tau (n)\\ \le g(M)-rM-(g(M)-M)\\ =(1-r)M,\\ (H_{r}x)(n)=g(x(n))-px(n)-f(n,x(n-\tau (n)\\ \ge g(m)-rm-(g(m)-m)\\ =(1-r)m.\end{array}$$

Hence, for any x ∈ Ω and n ∈ ℤ,

$$\begin{array}{ll}\hfill \left(T_{r}x\right)\left(n\right)& ={\left(r^{-h}-1\right)}^{-1}\sum _{i=1}^h{r}^{-i}\left(H_{p}x\right)\left(n+\left(i-1\right)k\right)\\ \le {\left(r^{-h}-1\right)}^{-1}\sum _{i=1}^h{r}^{-i}\left(1-r\right)M=M,\\ \hfill \left(T_{r}x\right)\left(n\right)& ={\left(r^{-h}-1\right)}^{-1}\sum _{i=1}^h{r}^{-i}\left(H_{p}x\right)\left(n+\left(i-1\right)k\right)\\ \ge {\left(r^{-h}-1\right)}^{-1}\sum _{i=1}^h{r}^{-i}\left(1-r\right)m=m.\end{array}$$

Hence, T _r (Ω) ⊆ Ω.

Since X is finite-dimensional and g(u), f(n, u) are continuous in u, one easily show that T _r is completely continuous in Ω. Therefore, T _r has a fixed point x ∈ Ω by Lemma 3.2, which is a ω = periodic solution of (1.1). The proof is complete. □

Proof of Theorem 1.2 Since g ∈ C ¹[m, M], max{g'(u): m ≤ u ≤ M} exists and max{g'(u): m ≤ u ≤ M} ≥ 1. Let p = max{g'(u): m ≤ u ≤ M}. If p = 1, then g(u) ≡ u on [m, M]. It is easy to check that any constant c ∈ [m, M] is a periodic solution of (1.1). Next, we assume that p > 1. Set Ω = {x ∈ X : m ≤ x(n) ≤ M for n ∈ ℤ}. Noting that the function g(u) - pu is nonincreasing in [m, M], we have for any x ∈ Ω,

$$g\left(M\right)-pM\le g\left(x\left(n\right)\right)-px\left(n\right)\le g\left(m\right)-pm,\forall n\in \mathbb{Z}.$$

For any x ∈ Ω and n ∈ ℤ,

$$\begin{array}{c}(H_{p}x)(n)=g(x(n))-px(n)-f(n,x(n-\tau (n)\\ \le g(m)-pm-(g(m)-m)\\ =(1-p)m,\\ (H_{p}x)(n)=g(x(n))-px(n)-f(n,x(n-\tau (n)\\ \ge g(M)-pM-(g(M)-M)\\ =(1-p)M.\end{array}$$

Hence, for any x ∈ Ω and n ∈ ℤ,

$$\begin{array}{ll}\hfill \left(T_{p}x\right)\left(n\right)& ={\left(p^{-h}-1\right)}^{-1}\sum _{i=1}^h{p}^{-i}\left(H_{p}x\right)\left(n+\left(i-1\right)k\right)\\ \ge {\left(p^{-h}-1\right)}^{-1}\sum _{i=1}^h{p}^{-i}\left(1-p\right)m=m,\\ \hfill \left(T_{p}x\right)\left(n\right)& ={\left(p^{-h}-1\right)}^{-1}\sum _{i=1}^h{p}^{-i}\left(H_{p}x\right)\left(n+\left(i-1\right)k\right)\\ \le {\left(p^{-h}-1\right)}^{-1}\sum _{i=1}^h{p}^{-i}\left(1-p\right)M=M.\end{array}$$

Hence, T _p (Ω) ⊆ Ω. T _p has a fixed point x ∈ Ω. The proof is complete. □