Global behavior of the solutions of some difference equations

Abstract

In this article we study the difference equation

$$x_{n+1}=\frac{a{x}_{n-l}{x}_{n-k}}{b{x}_{n-p}-c{x}_{n-q}},n=0,1,\dots ,$$

where the initial conditions x _-r , x _-r+1, x _-r+2,..., x ₀ are arbitrary positive real numbers, r = max{l, k, p, q} is nonnegative integer and a, b, c are positive constants: Also, we study some special cases of this equation.

1 Introduction

The purpose of this article is to investigate the global attractivity of the equilibrium point, and the asymptotic behavior of the solutions of the following difference equation

$$x_{n+1}=\frac{a{x}_{n-l}{x}_{n-k}}{b{x}_{n-p}-c{x}_{n-q}},n=0,1,\dots ,$$

(1)

where the initial conditions x _-r , x _-r+1, x _-r+2,..., x ₀ are arbitrary positive real numbers, r = max{l, k, p, q} is nonnegative integer and a, b, c are positive constants: Moreover, we obtain the form of the solution of some special cases of Equation 1 and some numerical simulations to the equation are given to illustrate our results.

Let us introduce some basic definitions and some theorems that we need in the sequel.

Let I be some interval of real numbers and let

$$f:I^{k+1}\to I,$$

be a continuously differentiable function. Then for every set of initial conditions x _-k , x _-k+1,..., x ₀ ∈ I, the difference equation

$$x_{n+1}=f\left(x_n,x_{n-1},\dots ,x_{n-k}\right),n=0,1,\dots ,$$

(2)

has a unique solution ${\left\{x_n\right\}}_{n=-k}^{\infty }\left[1\right]$.

A point $\bar{x}\in I$ is called an equilibrium point of Equation 2 if

$$\bar{x}=f\left(\bar{x},\bar{x},\dots ,\bar{x}\right).$$

That is, $x_n=\bar{x}$ for n ≥ 0, is a solution of Equation 2, or equivalently, $\bar{x}$ is a fixed point of f.

Definition 1 (Stability)

• (i) The equilibrium point $\bar{x}$ of Equation 2 is locally stable if for every ε > 0, there exists δ > 0 such that for all x _-k , x _-k+1 ,..., x _-1, x ₀ ∈ I with

  $$|x_{-k}-\bar{x}|+|x_{-k+1}-\bar{x}|+\cdots +|x_0-\bar{x}|<\delta ,$$

we have

$$|x_n-\bar{x}|<\epsilon \mathsf{\text{for all}}n\ge -k.$$

• (ii) The equilibrium point $\bar{x}$ of Equation 2 is locally asymptotically stable if $\bar{x}$ is locally stable solution of Equation 2 and there exists γ > 0, such that for all x _-k , x _-k+1,..., x _-1, x ₀ ∈ I with

  $$|x_{-k}-\bar{x}|+|x_{-k+1}-\bar{x}|+\dots +|x_0-\bar{x}|<\gamma ,$$

we have

$$\underset{n\to \infty }{lim}{x}_n=\bar{x}.$$

• (iii) The equilibrium point $\bar{x}$ of Equation 2 is global attractor if for all x _-k , x _-k+1,..., x _-1, x ₀ ∈ I, we have

  $$\underset{n\to \infty }{lim}{x}_n=\bar{x}.$$

• (iv) The equilibrium point $\bar{x}$ of Equation 2 is globally asymptotically stable if $\bar{x}$ is locally stable and $\bar{x}$ is also a global attractor of Equation 2.

• (v) The equilibrium point $\bar{x}$ of Equation 2 is unstable if $\bar{x}$ is not locally stable.

The linearized equation of Equation 2 about the equilibrium $\bar{x}$ is the linear difference equation

$$y_{n+1}={\sum }_{i=0}^k\frac{\partial f\left(\bar{x},\bar{x},\dots ,\bar{x}\right)}{\partial x_{n-i}}{y}_{n-i}.$$

(3)

Theorem A [2]

Assume that p, q ∈ R and k ∈ {0, 1, 2,...}. Then

$$\left|p\right|+\left|q\right|<1,$$

is a sufficient condition for the asymptotic stability of the difference equation

$$x_{n+1}+p{x}_n+q{x}_{n-k}=0,n=0,1,\dots .$$

Remark 1 Theorem A can be easily extended to a general linear equations of the form

$$x_{n+k}+p_1{x}_{n+k-1}+\dots +p_k{x}_n=0,n=0,1,\dots ,$$

(4)

where p ₁, p ₂,..., p _k ∈ R and k ∈ {1, 2,...}. Then Equation 4 is asymptotically stable provided that

$$\sum _{i=1}^k\left|p_i\right|<1.$$

Definition 2

(Fibonacci Sequence) The sequence ${\left\{F_m\right\}}_{m=0}^{\infty }=\left\{1,2,3,5,8,13,\dots \right\}$ i.e. F _m = F _m-1 + F _m-2, m ≥ 0, F _-2 = 0, F _-1 = 1 is called Fibonacci Sequence.

The nature of many biological systems naturally leads to their study by means of a discrete variable. Particular examples include population dynamics and genetics. Some elementary models of biological phenomena, including a single species population model, harvesting of fish, the production of red blood cells, ventilation volume and blood CO₂ levels, a simple epidemics model and a model of waves of disease that can be analyzed by difference equations are shown in [3]. Recently, there has been interest in so-called dynamical diseases, which correspond to physiological disorders for which a generally stable control system becomes unstable. One of the first papers on this subject was that of Mackey and Glass [4]. In that paper they investigated a simple first order difference-delay equation that models the concentration of blood-level CO₂. They also discussed models of a second class of diseases associated with the production of red cells, white cells, and platelets in the bone marrow.

The study of the nonlinear rational difference equations of a higher order is quite challenging and rewarding, and the results about these equations offer prototypes towards the development of the basic theory of the global behavior of nonlinear difference equations of a big order, recently, many researchers have investigated the behavior of the solution of difference equations for example: Elabbasy et al. [5] investigated the global stability, periodicity character and gave the solution of special case of the following recursive sequence

$$x_{n+1}=a{x}_n-\frac{b{x}_n}{c{x}_n-d{x}_{n-1}}.$$

Elabbasy et al. [6] investigated the global stability, boundedness, periodicity character and gave the solution of some special cases of the difference equation

$$x_{n+1}=\frac{\alpha x_{n-k}}{\beta +\gamma {\prod }_{i=0}^k{x}_{n-i}}.$$

Elabbasy et al. [7] investigated the global stability character, boundedness and the periodicity of solutions of the difference equation

$$x_{n+1}=\frac{\alpha x_n+\beta x_{n-1}+\gamma x_{n-2}}{A{x}_n+B{x}_{n-1}+C{x}_{n-2}}.$$

El-Metwally et al. [8] investigated the asymptotic behavior of the population model:

$$x_{n+1}=\alpha +\beta x_{n-1}{e}^{-x_n},$$

where α is the immigration rate and β is the population growth rate.

Yang et al. [9] investigated the invariant intervals, the global attractivity of equilibrium points and the asymptotic behavior of the solutions of the recursive sequence

$$x_{n+1}=\frac{a{x}_{n-1}+b{x}_{n-2}}{c+d{x}_{n-1}{x}_{n-2}}.$$

Cinar [10, 11] has got the solutions of the following difference equations

$$x_{n+1}=\frac{x_{n-1}}{1+a{x}_n{x}_{n-1}},x_{n+1}=\frac{x_{n-1}}{-1+a{x}_n{x}_{n-1}}.$$

Aloqeili [12] obtained the form of the solutions of the difference equation

$$x_{n+1}=\frac{x_{n-1}}{a-x_n{x}_{n-1}}.$$

Yalçinkaya [13] studied the following nonlinear difference equation

$$x_{n+1}=\alpha +\frac{x_{n-m}}{x_n^k}.$$

For some related work see [1–29].

The article proceeds as follows. In Sect. 2 we show that when 2a |b - c| + a(b + c) < (b - c)², then the equilibrium point of Equation 1 is locally asymptotically stable. In Sect. 3 we prove that the equilibrium point of Equation 1 is global attractor. In Sect. 4 we give the solutions of some special cases of Equation 1 and give a numerical examples of each case and draw it by using Matlab 6.5.

2 Local stability of Equation 1

In this section we investigate the local stability character of the solutions of Equation 1. Equation 1 has a unique positive equilibrium point and is given by

$$\overline{x}=\frac{a{\overline{x}}^2}{b\overline{x}-c\overline{x}},$$

if a ≠ b-c, b ≠ c, then the unique equilibrium point is $\bar{x}=0.$

Let f : (0, ∞)⁴ → (0, ∞) be a function defined by

$$f\left(u,v,w,s\right)=\frac{auv}{bw-cs}.$$

(5)

Therefore, it follows that

$$f_u\left(u,v,w,s\right)=\frac{av}{\left(bw-cs\right)},f_v\left(u,v,w,s\right)=\frac{au}{\left(bw-cs\right)},$$

$$f_w\left(u,v,w,s\right)=\frac{-bauv}{{\left(bw-cs\right)}^2},f_s\left(u,v,w,s\right)=\frac{cauv}{{\left(bw-cs\right)}^2},$$

we see that

$$f_u\left(\bar{x},\bar{x},\bar{x},\bar{x}\right)=\frac{a}{\left(b-c\right)},f_v\left(\bar{x},\bar{x},\bar{x},\bar{x}\right)=\frac{a}{\left(b-c\right)},$$

$$f_w\left(\bar{x},\bar{x},\bar{x},\bar{x}\right)=\frac{-ab}{{\left(b-c\right)}^2},f_s\left(\bar{x},\bar{x},\bar{x},\bar{x}\right)=\frac{ac}{{\left(b-c\right)}^2}.$$

The linearized equation of Equation 1 about $\bar{x}$ is

$$y_{n+1}+\frac{a}{\left(b-c\right)}{y}_{n-1}+\frac{a}{\left(b-c\right)}{y}_{n-k}-\frac{ab}{{\left(b-c\right)}^2}{y}_{n-p}+\frac{ac}{{\left(b-c\right)}^2}{y}_{n-q}=0.$$

(6)

Theorem 1

Assume that

$$a(3\zeta -\eta )<{(b-c)}^2.$$

where ζ = max{b, c}, η = min{b, c}. Then the equilibrium point of Equation 1 is locally asymptotically stable.

Proof: It is follows by Theorem A that Equation 6 is asymptotically stable if

$$\left|\frac{a}{\left(b-c\right)}\right|+\left|\frac{a}{\left(b-c\right)}\right|+\left|\frac{ab}{{\left(b-c\right)}^2}\right|+\left|\frac{ab}{{\left(b-c\right)}^2}\right|<1,$$

or

$$\left|\frac{2a}{\left(b-c\right)}\right|+\left|\frac{a\left(b+c\right)}{{\left(b-c\right)}^2}\right|<1,$$

and so

$$2a|b-c|+a\left(b+c\right)<{\left(b-c\right)}^2.$$

The proof is complete.

3 Global attractivity of the equilibrium point of Equation 1

In this section we investigate the global attractivity character of solutions of Equation 1.

We give the following two theorems which is a minor modification of Theorem A.0.2 in [1].

Theorem 2

Let [a, b] be an interval of real numbers and assume that

$$f:{[a,b]}^{k+1}\to [a,b],$$

is a continuous function satisfying the following properties:

• (i) f(x ₁, x ₂,...., x _k+1) is non-increasing in one component (for example x _t ) for each x _r (r ≠ t) in [a, b] and non-decreasing in the remaining components for each x _t in [a, b].

• (ii) If $\left(m,M\right)\in \left[a,b\right]\times \left[a,b\right]$ is a solution of the system

M = f(M, M,...,M, m, M,...,M, M) and m = f(m, m,...,m, M, m,...m, m) implies

$$m=M.$$

Then Equation 2 has a unique equilibrium $\bar{x}\in \left[a,b\right]$ and every solution of Equation 2 converges to $\bar{x}$

Proof: Set

$$m_0=a\mathsf{\text{and}}{M}_0=b,$$

and for each i = 1, 2,...set

$$m_i=f\left(m_{i-1},m_{i-1},\dots ,m_{i-1},M_{i-1},m_{i-1},\dots ,m_{i-1},m_{i-1}\right),$$

and

$$M_i=f\left(M_{i-1},M_{i-1},\dots ,M_{i-1},m_{i-1},M_{i-1},\dots ,M_{i-1},M_{i-1}\right).$$

Now observe that for each i ≥ 0,

$$a=m_0\le m_1\le \dots \le m_i\le \dots \le M_i\le \dots \le M_1\le M_0=b,$$

and

$$m_i\le x_p\le M_i\mathsf{\text{for}}p\ge \left(k+1\right)i+1.$$

Set

$$m=\underset{x\to \infty }{lim}{m}_i\mathsf{\text{and}}M=\underset{i\to \infty }{lim}{M}_i.$$

Then

$$M\ge \underset{i\to \infty }{lim}sup{x}_i\ge lim\underset{i\to \infty }{inf}{x}_i\ge m$$

and by the continuity of f,

M = f(M, M,...,M, m, M,...,M, M) and m = f(m, m,...,m, M, m,...m, m).

In view of (ii),

$$m=M=\bar{x},$$

from which the result follows.

Theorem 3

Let [a, b] be an interval of real numbers and assume that

$$f:{[a,b]}^{k+1}\to [a,b],$$

is a continuous function satisfying the following properties:

• (i) f(x ₁, x ₂,...,x _k+1) is non-increasing in one component (for example x _t ) for each x _r (r ≠ t) in [a, b] and non-increasing in the remaining components for each x _t in [a, b].

• (ii) If (m, M)∈[a, b] × [a, b] is a solution of the system

M = f(m, m,...,m, M, m,...m, m) and m = f(M, M,...,M, m, M,...,M, M)' implies

$$m=M.$$

Then Equation 2 has a unique equilibrium $\bar{x}\in \left[a,b\right]$ and every solution of Equation 2 converges to $\bar{x}$

Proof: As the proof of Theorem 2 and will be omitted.

Theorem 4

The equilibrium point $\bar{x}$ of Equation 1 is global attractor if c ≠ a.

Proof: Let p, q are a real numbers and assume that $f:{\left[p,q\right]}^4\to \left[p,q\right]$ be a function defined by Equation 5, then we can easily see that the function f(u, v, w, s) increasing in s and decreasing in w.

Case (1) If bw-cs > 0, then we can easily see that the function f(u, v, w, s)

increasing in u, v, s and decreasing in w.

Suppose that (m, M) is a solution of the system

M = f(m, m, M, m) and M = f(M, M, m, M).

Then from Equation 1, we see that

$$m=\frac{a{m}^2}{bM-cm},M=\frac{a{M}^2}{bm-cM},$$

$$bM=cm+am,bm=cM+aM,$$

then

$$\left(M-m\right)\left(b+c+a\right)=0.$$

Thus

$$M=m.$$

It follows by Theorem 2 that $\bar{x}$ is a global attractor of Equation 1 and then the proof is complete.

Case (2) If bw-cs < 0, then we can easily see that the function f(u, v, w, s) decreasing in u, v, w and increasing in s.

Suppose that (m, M) is a solution of the system

M = f(m, m, m, M) and m = f(M, M, M, m).

Then from Equation 1, we see that

$$M=\frac{a{m}^2}{bm-cM},m=\frac{a{M}^2}{bM-cm},$$

$$bmM-c{M}^2=a{m}^2,bmM-c{m}^2=a{M}^2,$$

then

$$\left(M^2-m^2\right)\left(c-a\right)=0,a\ne c.$$

Thus,

$$M=m.$$

It follows by the Theorem 3 that $\bar{x}$ is a global attractor of Equation 1 and then the proof is complete.

4 Special cases of Equation 1

4.1 Case (1)

In this section we study the following special case of Equation 1

$$x_{n+1}=\frac{x_n{x}_{n-1}}{x_n-x_{n-1}},$$

(7)

where the initial conditions x _-1, x ₀ are arbitrary positive real numbers.

Theorem 5

Let ${\left\{x_n\right\}}_{n=-1}^{\infty }$ be a solution of Equation 7. Then for n = 0, 1,...

$$x_n=\frac{{\left(-1\right)}^{n}hk}{F_{n-1}k-F_{n-2}h},$$

where x _-1 = k, x ₀ = h and F _n-1 , F _n-2are the Fibonacci terms.

Proof: For n = 0 the result holds. Now suppose that n > 0 and that our assumption holds for n-1, n-2. That is;

$$x_{n-2}=\frac{{\left(-1\right)}^{n-2}hk}{F_{n-3}k-F_{n-4}h},x_{n-1}=\frac{{\left(-1\right)}^{n-1}hk}{F_{n-2}k-F_{n-3}h}.$$

Now, it follows from Equation 7 that

$$\begin{array}{lll}\hfill x_n& =\frac{x_{n-1}{x}_{n-2}}{x_{n-1}-x_{n-2}}=\frac{\left(\frac{{\left(-1\right)}^{n-1}hk}{F_{n-2}k-F_{n-3}h}\right)\left(\frac{{\left(-1\right)}^{n-2}hk}{F_{n-3}k-F_{n-4}h}\right)}{\left(\frac{{\left(-1\right)}^{n-1}hk}{F_{n-2}k-F_{n-3}h}-\frac{{\left(-1\right)}^{n-2}hk}{F_{n-3}k-F_{n-4}h}\right)}& \hfill \text{(1)}\\ =\frac{\left(\frac{{\left(-1\right)}^{n-1}hk}{F_{n-2}k-F_{n-3}h}\right)\left(\frac{-1}{F_{n-3}k-F_{n-4}h}\right)}{\left(\frac{1}{F_{n-2}k-F_{n-3}h}+\frac{1}{F_{n-3}k-F_{n-4}h}\right)}=\frac{{\left(-1\right)}^{n}hk}{\left(F_{n-2}k-F_{n-3}h+F_{n-3}k-F_{n-4}h\right)}& \hfill \text{(2)}\\ =\frac{{\left(-1\right)}^{n}hk}{F_{n-1}k-F_{n-2}h}.n& \hfill \text{(3)}\\ \hfill \text{(4) }\end{array}$$

Hence, the proof is completed.

For confirming the results of this section, we consider numerical example for x _-1 = 11, x ₀ = 4 (see Figure 1), and for x _-1 = 6, x ₀ = 15 (see Figure 2), since the solutions take the forms {6, -12, 4, -3, 1.714286, -1.090909, .6666667, -.4137931, .2553191,....}, {-60, 10, -8.571428, 4.615385, -3, 1.818182, -1.132075, .6976744,...}.

Figure 1

This figure shows the solution of $x_{n+1}=\frac{x_n{x}_{n-1}}{x_n-x_{n-1}},$ where x _-1 = 11, x ₀ = 4.

Figure 2

This figure shows the solution of $x_{n+1}=\frac{x_n{x}_{n-1}}{x_n-x_{n-1}},$ for x _-1 = 6, x ₀ = 15.

4.2 Case (2)

In this section we study the following special case of Equation 1

$$x_{n+1}=\frac{x_{n-1}{x}_{n-2}}{x_{n-1}-x_{n-2}},$$

(8)

where the initial conditions x _-2, x _-1, x ₀ are arbitrary positive real numbers.

Theorem 6

Let ${\left\{x_n\right\}}_{n=-2}^{\infty }$ be a solution of Equation 8. Then $x_1=\frac{rk}{k-r}$, for n = 1, 2,...

$$x_{n+1}=\frac{hkr}{g_{n-4}hk+g_{n-3}kr+g_{n-2}hr},$$

where x _-2 = r, x _-1 = k, x ₀ = h, ${\left\{g_m\right\}}_{m=0}^{\infty }=\left\{1,-2,0,3,-2,-3,\dots \right\},$ i.e., g _m = g _m-2+ g _m-3, m ≥ 0, g _-3 = 0, g _-2 = -1, g _-1 = 1.

Proof: For n = 1, 2 the result holds. Now suppose that n > 1 and that our assumption holds for n - 1, n - 2. That is;

$x_{n-2}=\frac{hkr}{g_{n-7}hk+g_{n-6}kr+g_{n-5}hr},$ $x_{n-1}=\frac{hkr}{g_{n-6}hk+g_{n-5}kr+g_{n-4}hr}.$ Now, it follows from Equation 8 that

$$\begin{array}{lll}\hfill x_{n+1}& =\frac{x_{n-1}{x}_{n-2}}{x_{n-1}-x_{n-2}}& \hfill \text{(1)}\\ =\frac{\left(\frac{hkr}{g_{n-6}hk+g_{n-5}kr+g_{n-4}hr}\right)\left(\frac{hkr}{g_{n-7}hk+g_{n-6}kr+g_{n-5}hr}\right)}{\left(\frac{hkr}{g_{n-6}hk+g_{n-5}kr+g_{n-4}hr}-\frac{hkr}{g_{n-7}hk+g_{n-6}kr+g_{n-5}hr}\right)}& \hfill \text{(2)}\\ =\frac{hkr}{\left(g_{n-7}hk+g_{n-6}kr+g_{n-5}hr-g_{n-6}hk+g_{n-5}kr+g_{n-4}hr\right)}& \hfill \text{(3)}\\ =\frac{hkr}{g_{n-4}hk+g_{n-3}kr+g_{n-2}hr}.& \hfill \text{(4)}\\ \hfill \text{(5)}\end{array}$$

Hence, the proof is completed.

Assume that x _-2 = 8, x _-1 = 15, x ₀ = 7, then the solution will be {17.14286, -13.125, 11.83099, 7.433628, -6.222222, -20, 3.387097, -9.032259,...}(see Figure 3).

Figure 3

This figure shows the solution of $x_{n+1}=\frac{x_{n-1}{x}_{n-2}}{x_{n-1}-x_{n-2}},$ where x _-2 = 8, x _-1 = 15, x ₀ = 7.

The proof of following cases can be treated similarly.

4.3 Case (3)

Let x _-2 = r, x _-1 = k, x ₀ = h, $\prod _{i=0}^{-1}{A}_i=1$ and F _2i-1, F _2i , F _2i+1(where i = 0 to n) are the Fibonacci terms. Then the solution of the difference equation

$$x_{n+1}=\frac{x_{n-1}{x}_{n-2}}{x_n-x_{n-2}},$$

(9)

is given by

$$x_{2n}=\frac{h\prod _{i=0}^{n-1}\left(F_{2i-1}h-F_{2i}r\right)}{\prod _{i=0}^{n-1}\left(F_{2i+1}r-F_{2i}h\right)},x_{2n+1}=\frac{kr\prod _{i=0}^{n-1}\left(F_{2i+1}r-F_{2i}h\right)}{\prod _{i=0}^n\left(F_{2i-1}h-F_{2i}r\right)},n=0,1,....$$

Figure 4 shows the solution when x _-2 = 9, x _-1 = 12, x ₀ = 17.

Figure 4

This figure shows the solution of $x_{n+1}=\frac{x_{n-1}{x}_{n-2}}{x_n-x_{n-2}},$ when x _-2 = 9, x _-1 = 12, x ₀ = 17.

4.4 Case (4)

Let x _-2 = r, x _-1 = k, x ₀ = h. Then the solution of the following difference equation

$$x_{n+1}=\frac{x_{n-1}{x}_n}{x_n-x_{n-2}}$$

(10)

is given by

$$x_{2n-1}={\left(\frac{h}{h-r}\right)}^{n}k,x_{2n}=\frac{h^{n+1}}{r^n},n=0,1,\dots .$$

Figure 5 shows the solution when x _{- 2}= 21, x _{- 1}= 6, x ₀ = 3.

Figure 5

This figure shows the solution of $x_{n+1}=\frac{x_{n-1}{x}_n}{x_n-x_{n-2}},$ where x _-2 = 21, x _-1 = 6, x ₀ = 3.

4.5 Case (5)

Let x _{- 2}= r, x _{- 1}= k, x ₀ = h. Then the solution of the following difference equation

$$x_{n+1}=\frac{x_{n-1}{x}_n}{x_{n-1}-x_{n-2}},$$

(11)

is given by

$$x_{4n}=\frac{h{\left(hk\right)}^{2n}}{{\left(rk\left(h-k\right)\left(k-r\right)\right)}^n},x_{4n+1}=\frac{{\left(hk\right)}^{2n+1}}{{\left(rk\left(h-k\right)\right)}^n{\left(k-r\right)}^{n+1}},$$

$$x_{4n+2}=\frac{h{\left(hk\right)}^{2n+1}}{{\left(\left(h-k\right)\left(k-r\right)\right)}^{n+1}{\left(rk\right)}^n},x_{4n+3}=\frac{{\left(hk\right)}^{2n}}{{\left(r\left(h-k\right)\left(k-r\right)\right)}^{n+1}{k}^n},n=0,1,\dots .$$

Figure 6 shows the solution when x _{- 2}= 9, x _{- 1}= 5, x ₀ = 4.

Figure 6

This figure shows the solution of $x_{n+1}=\frac{x_{n-1}{x}_n}{x_{n-1}-x_{n-2}},$ for x _-2 = 9, x _-1 = 5, x ₀ = 4.

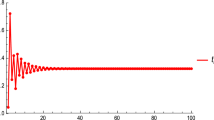
Figure 7 shows the solution when x _{- 2}= .9, x _{- 1}= 5, x ₀ = .4.

Figure 7

This figure shows the solution of $x_{n+1}=\frac{x_{n-1}{x}_n}{x_{n-1}-x_{n-2}},$ when x _-2 = 0.9, x _-1 = 5, x ₀ = 0.4.

4.6 Case (6)

Let x _{- 2}= r, x _{- 1}= k, x ₀ = h, Then the solution of the following difference equation

$$x_{n+1}=\frac{x_{n-2}{x}_n}{x_n-x_{n-2}},$$

(12)

is given by

$$x_n=\frac{hkr}{u_{n-3}hr+u_{n-2}hk+u_{n-1}kr},n=0,1,\dots ,$$

Where ${\left\{u_m\right\}}_{m=0}^{\infty }=\left\{-1,1,0,-1,2,-2,1,1,-3,\dots \right\}$ i. e. u _m = u _m-1- u _m-3, m ≥ 0, u _-3 = 0, u _-2 = 0, u _-1 = 1.

Figure 8 shows the solution when x _-2 = 11, x _-1 = 6, x ₀ = 17.

Figure 8

This figure shows the solution of $x_{n+1}=\frac{x_{n-2}{x}_n}{x_n-x_{n-2}},$ where x _-2 = 11, x -1 = 6, x ₀ = 17.

4.7 Case (7)

Let x _-2 = r, x _-1 = k, x ₀ = h and F _n-1F_{, n-2}, F _n are the Fibonacci terms.

Then the solution of the following difference equation

$$x_{n+1}=\frac{x_{n-2}{x}_n}{x_{n-1}-x_{n-2}},$$

(13)

is given by

$$x_{2n}=\frac{hkr}{\left(F_{n-2}k-F_{n-1}r\right)\left(F_{n-2}h-F_{n-1}k\right)},$$

$$x_{2n+1}=\frac{hkr}{\left(F_{n-1}k-F_{n}r\right)\left(F_{n-2}h-F_{n-1}k\right)},n=0,1,\dots .$$

Figure 9 shows the solution when x _{- 2}= 8, x _{- 1}= 5, x ₀ = 0.9.

Figure 9

This figure shows the solution of $x_{n+1}=\frac{x_{n-2}{x}_n}{x_{n-1}-x_{n-2}}$ when x _-2 = 8, x _-1 = 5, x ₀ = 0.9.