Best proximity points of generalized almost ψ-Geraghty contractive non-self-mappings

Abstract

In this paper, we introduce the new notion of almost ψ-Geraghty contractive mappings and investigate the existence of a best proximity point for such mappings in complete metric spaces via the weak P-property. We provide an example to validate our best proximity point theorem. The obtained results extend, generalize, and complement some known fixed and best proximity point results from the literature.

MSC:47H10, 54H25, 46J10, 46J15.

1 Introduction and preliminaries

Non-self-mappings are among the intriguing research directions in fixed point theory. This is evident from the increase of the number of publications related with such maps. A great deal of articles on the subject investigate the non-self-contraction mappings on metric spaces. Let $(X,d)$ be a metric space and A and B be nonempty subsets of X. A mapping $T:A\to B$ is said to be a k-contraction if there exists $k\in [0,1)$ such that $d(Tx,Ty)\le kd(x,y)$ for any $x,y\in A$. It is clear that a k-contraction coincides with the celebrated Banach fixed point theorem (Banach contraction principle) [1] if one takes $A=B$ where the induced metric space $(A,d{|}_A)$ is complete.

In nonlinear analysis, the theory of fixed points is an essential instrument to solve the equation $Tx=x$ for a self-mapping T defined on a subset of an abstract space such as a metric space, a normed linear space or a topological vector space. Following the Banach contraction principle, most of the fixed point results have been proved for a self-mapping defined on an abstract space. It is quite natural to investigate the existence and uniqueness of a non-self-mapping $T:A\to B$ which does not possess a fixed point. If a non-self-mapping $T:A\to B$ has no fixed point, then the answer of the following question makes sense: Is there a point $x\in X$ such that the distance between x and Tx is closest in some sense? Roughly speaking, best proximity theory investigates the existence and uniqueness of such a closest point x. We refer the reader to [2–9] and [10–32] for further discussion of best proximity.

Definition 1.1 Let $(X,d)$ be a metric space and $A,B\subset X$. We say that $x^{\ast }\in A$ is a best proximity point of the non-self-mapping $T:A\to B$ if the following equality holds:

$$d(x^{\ast },T{x}^{\ast })=d(A,B),$$

(1)

where $d(A,B)=inf\{d(x,y):x\in A,y\in B\}$.

It is clear that the notion of a fixed point coincided with the notion of a best proximity point when the underlying mapping is a self-mapping.

Let $(X,d)$ be a metric space. Suppose that A and B are nonempty subsets of a metric space $(X,d)$. We define the following sets:

$$\begin{array}{r}{A}_0=\{x\in A:d(x,y)=d(A,B)\text{ for some }y\in B\},\\ B_0=\{y\in B:d(x,y)=d(A,B)\text{ for some }x\in A\}.\end{array}$$

(2)

In [17], the authors presented sufficient conditions for the sets $A_0$ and $B_0$ to be nonempty.

In 1973 Geraghty [33] introduced the class S of functions $\beta :[0,\mathrm{\infty })\to [0,1)$ satisfying the following condition:

$$\beta (t_n)\to 1\text{implies}{t}_n\to 0.$$

(3)

The author defined contraction mappings via functions from this class and proved the following result.

Theorem 1.1 (Geraghty [33])

Let $(X,d)$ be a complete metric space and $T:X\to X$ be an operator. If T satisfies the following inequality:

$$d(Tx,Ty)\le \beta (d(x,y))d(x,y)\mathit{\text{for any }}x,y\in X,$$

(4)

where $\beta \in S$, then T has a unique fixed point.

Recently, Caballero et al. [6] introduced the following contraction.

Definition 1.2 ([6])

Let A, B be two nonempty subsets of a metric space $(X,d)$. A mapping $T:A\to B$ is said to be a Geraghty-contraction if there exists $\beta \in S$ such that

$$d(Tx,Ty)\le \beta (d(x,y))d(x,y)\mathit{\text{for any }}x,y\in A.$$

(5)

Based on Definition 1.2, the authors [6] obtained the following result.

Theorem 1.2 (See [6])

Let $(A,B)$ be a pair of nonempty closet subsets of a complete metric space $(X,d)$ such that $A_0$ is nonempty. Let $T:A\to B$ be a continuous, Geraghty-contraction satisfying $T(A_0)\subseteq B_0$. Suppose that the pair $(A,B)$ has the P-property, then there exists a unique $x^{\ast }$ in A such that $d(x^{\ast },T{x}^{\ast })=d(A,B)$.

The P-property mentioned in the theorem above has been introduced in [29].

Definition 1.3 Let $(A,B)$ be a pair of nonempty subsets of a metric space $(X,d)$ with $A_0\ne \mathrm{\varnothing }$. Then the pair $(A,B)$ is said to have the P-property if and only if for any $x_1,x_2\in A_0$ and $y_1,y_2\in B_0$,

$$d(x_1,y_1)=d(A,B)\mathit{\text{and}}d(x_2,y_2)=d(A,B)\Rightarrow d(x_1,x_2)=d(y_1,y_2).$$

(6)

It is easily seen that for any nonempty subset A of $(X,d)$, the pair $(A,A)$ has the P-property. In [29], the author proved that any pair $(A,B)$ of nonempty closed convex subsets of a real Hilbert space H satisfies the P-property.

Recently, Zhang et al. [34] defined the following notion, which is weaker than the P-property.

Definition 1.4 Let $(A,B)$ be a pair of nonempty subsets of a metric space $(X,d)$ with $A_0\ne \mathrm{\varnothing }$. Then the pair $(A,B)$ is said to have the weak P-property if and only if for any $x_1,x_2\in A_0$ and $y_1,y_2\in B_0$,

$$d(x_1,y_1)=d(A,B)\mathit{\text{and}}d(x_2,y_2)=d(A,B)\Rightarrow d(x_1,x_2)\le d(y_1,y_2).$$

(7)

Let Ψ denote the class of functions $\psi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ satisfying the following conditions:

• (a) ψ is nondecreasing;

• (b) ψ is subadditive, that is, $\psi (s+t)\le \psi (s)+\psi (t)$;

• (c) ψ is continuous;

• (d) $\psi (t)=0\iff t=0$.

The notion of ψ-Geraghty contraction has been introduced very recently in [11], as an extension of Definition 1.2.

Definition 1.5 Let A, B be two nonempty subsets of a metric space $(X,d)$. A mapping $T:A\to B$ is said to be a ψ-Geraghty contraction if there exist $\beta \in S$ and $\psi \in \mathrm{\Psi }$ such that

$$\psi (d(Tx,Ty))\le \beta \left(\psi (d(x,y))\right)\psi (d(x,y))\mathit{\text{for any }}x,y\in A.$$

(8)

Remark 1.1 Notice that since $\beta :[0,\mathrm{\infty })\to [0,1)$, we have

$$\begin{array}{r}\psi (d(Tx,Ty))\le \beta \left(\psi (d(x,y))\right)\psi (d(x,y))<\psi (d(x,y))\\ \text{for any }x,y\in A\text{ with }x\ne y.\end{array}$$

(9)

In [11], the author also proved the following best proximity point theorem.

Theorem 1.3 (See [11])

Let $(A,B)$ be a pair of nonempty closed subsets of a complete metric space $(X,d)$ such that $A_0$ is nonempty. Let $T:A\to B$ be a ψ-Geraghty contraction satisfying $T(A_0)\subseteq B_0$. Suppose that the pair $(A,B)$ has the P-property. Then there exists a unique $x^{\ast }$ in A such that $d(x^{\ast },T{x}^{\ast })=d(A,B)$.

2 Main results

Our main results are based on the following definition which is a generalization of Definition 1.5.

Definition 2.1 Let A, B be two nonempty subsets of a metric space $(X,d)$. A mapping $T:A\to B$ is said to be a generalized almost ψ-Geraghty contraction if there exist $\beta \in S$ and $\psi \in \mathrm{\Psi }$ such that

$$\psi (d(Tx,Ty))\le \beta \left(\psi (M(x,y))\right)\psi (M(x,y)-d(A,B))+L\psi (N(x,y)-d(A,B))$$

(10)

for all $x,y\in A$ where $L\ge 0$,

$$\begin{array}{c}M(x,y)=max\{d(x,y),d(x,Tx),d(y,Ty)\},\hfill \\ N(x,y)=min\{d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)\}.\hfill \end{array}$$

Now, we state and prove our main theorem about existence and uniqueness of a best proximity point for a non-self-mapping satisfying a generalized almost ψ-Geraghty contraction.

Theorem 2.1 Let $(A,B)$ be a pair of nonempty closed subsets of a complete metric space $(X,d)$ such that $A_0$ is nonempty. Let $T:A\to B$ be a generalized almost ψ-Geraghty contraction satisfying $T(A_0)\subseteq B_0$. Assume that the pair $(A,B)$ has the weak P-property. Then T has a unique best proximity point in A.

Proof Since the subset $A_0$ is not empty, we can take $x_0$ in $A_0$. Taking into account that $T{x}_0\in T(A_0)\subseteq B_0$, we can find $x_1\in A_0$ such that $d(x_1,T{x}_0)=d(A,B)$. Further, since $T{x}_1\in T(A_0)\subseteq B_0$, it follows that there is an element $x_2$ in $A_0$ such that $d(x_2,T{x}_1)=d(A,B)$. Recursively, we obtain a sequence $\{x_n\}$ in $A_0$ satisfying

$$d(x_{n+1},T{x}_n)=d(A,B)\text{for any }n\in \mathbb{N}.$$

(11)

Since the pair $(A,B)$ has the weak P-property, we deduce

$$d(x_n,x_{n+1})\le d(T{x}_{n-1},T{x}_n)\text{for any }n\in \mathbb{N}.$$

(12)

Due to the triangle inequality together with the equality (11) we have

$$d(x_{n-1},T{x}_{n-1})\le d(x_{n-1},x_n)+d(x_n,T{x}_{n-1})=d(x_{n-1},x_n)+d(A,B).$$

Analogously, combining the equalities (11) and (12) with the triangle inequality we obtain

$$d(x_n,T{x}_n)\le d(x_n,x_{n+1})+d(x_{n+1},T{x}_n)=d(x_n,x_{n+1})+d(A,B).$$

(13)

Consequently, we have

$$\begin{array}{rcl}M(x_{n-1},x_n)& =& max\{d(x_{n-1},x_n),d(x_{n-1},T{x}_{n-1}),d(x_n,T{x}_n)\}\\ \le & max\{d(x_{n-1},x_n),d(x_n,x_{n+1})\}+d(A,B).\end{array}$$

(14)

Also note that

$$\begin{array}{r}N(x_{n-1},x_n)-d(A,B)\\ =min\{d(x_{n-1},T{x}_{n-1}),d(x_n,T{x}_n),d(x_{n-1},T{x}_n),d(x_n,T{x}_{n-1})\}-d(A,B)\\ \le min\{d(x_{n-1},T{x}_{n-1}),d(x_n,T{x}_n),d(x_{n-1},T{x}_n),d(A,B)\}-d(A,B)\\ =d(A,B)-d(A,B)=0.\end{array}$$

(15)

If there exists $n_0\in \mathbb{N}$ such that $d(x_{n_0},x_{n_0+1})=0$, then the proof is completed. Indeed,

$$0=d(x_{n_0},x_{n_0+1})=d(T{x}_{n_0-1},T{x}_{n_0}),$$

(16)

and consequently, $T{x}_{n_0-1}=T{x}_{n_0}$. Therefore, we conclude that

$$d(A,B)=d(x_{n_0},T{x}_{n_0-1})=d(x_{n_0},T{x}_{n_0}).$$

(17)

For the rest of the proof, we suppose that $d(x_n,x_{n+1})>0$ for all $n\in \mathbb{N}$. In view of the fact that T is a generalized almost ψ-Geraghty contraction, we have

$$\begin{array}{rl}\psi (d(x_n,x_{n+1}))& \le \psi (d(T{x}_{n-1},T{x}_n))\\ \le \beta \left(\psi (M(x_{n-1},x_n))\right)\psi (M(x_{n-1},x_n)-d(A,B))\\ +L\psi (N(x_{n-1},x_n)-d(A,B))\\ =\beta \left(\psi (M(x_{n-1},x_n))\right)\psi (M(x_{n-1},x_n)-d(A,B))+L\psi (0)\\ =\beta \left(\psi (M(x_{n-1},x_n))\right)\psi (M(x_{n-1},x_n)-d(A,B))\\ <\psi (M(x_{n-1},x_n)-d(A,B)).\end{array}$$

(18)

Taking into account the inequalities (14) and (18), we deduce that

$$\psi (d(x_n,x_{n+1}))<\psi (M(x_{n-1},x_n)-d(A,B))\le \psi (max\{d(x_{n-1},x_n),d(x_n,x_{n+1})\}).$$

If for some n, $max\{d(x_{n-1},x_n),d(x_n,x_{n+1})\}=d(x_n,x_{n+1})$, then we get

$$\psi (d(x_n,x_{n+1}))<\psi (d(x_n,x_{n+1})),$$

which is a contradiction. Therefore, we must have

$$M(x_{n-1},x_n)\le max\{d(x_{n-1},x_n),d(x_n,x_{n+1})\}+d(A,B)=d(x_{n-1},x_n)+d(A,B)$$

(19)

for all $n\in \mathbb{N}$. Regarding the inequality (18), we see that

$$\begin{array}{rl}\psi (d(x_n,x_{n+1}))& =\psi (d(T{x}_{n-1},T{x}_n))\\ \le \beta \left(\psi (M(x_{n-1},x_n))\right)\psi (d(x_{n-1},x_n))\\ <\psi (d(x_{n-1},x_n))\end{array}$$

(20)

holds for all $n\in \mathbb{N}$. Since ψ is nondecreasing, then $d(x_n,x_{n+1})<d(x_{n-1},x_n)$ for all n. Consequently, the sequence $\{d(x_n,x_{n+1})\}$ is decreasing and is bounded below and hence ${lim}_{n\to \mathrm{\infty }}d(x_n,x_{n+1})=s\ge 0$ exists. Assume that $s>0$. Rewrite (20) as

$$\frac{\psi (d(x_{n+1},x_{n+2}))}{\psi (d(x_n,x_{n+1}))}\le \beta \left(\psi (M(x_n,x_{n+1}))\right)\le 1$$

for each $n\ge 1$. Taking the limit of both sides as $n\to \mathrm{\infty }$, we find

$$\underset{n\to \mathrm{\infty }}{lim}\beta \left(\psi (M(x_n,x_{n+1}))\right)=1.$$

On the other hand, since $\beta \in S$, we conclude ${lim}_{n\to \mathrm{\infty }}\psi (M(x_n,x_{n+1}))=0$, that is,

$$s=\underset{n\to \mathrm{\infty }}{lim}d(x_n,x_{n+1})=0.$$

(21)

Since $d(x_n,T{x}_{n-1})=d(A,B)$ holds for all $n\in \mathbb{N}$ and $(A,B)$ satisfies the weak P-property, then for all $m,n\in \mathbb{N}$, we can write

$$d(x_m,x_n)\le d(T{x}_{m-1},T{x}_{n-1}).$$

(22)

From (13), we deduce

$$\begin{array}{rl}M(x_m,x_n)& =max\{d(x_m,x_n),d(x_m,T{x}_m),d(x_n,T{x}_n)\}\\ \le max\{d(x_m,x_n),d(x_m,x_{m+1}),d(x_n,x_{n+1})\}+d(A,B).\end{array}$$

By using ${lim}_{n\to \mathrm{\infty }}d(x_n,x_{n+1})=0$, we get

$$\underset{m,n\to \mathrm{\infty }}{lim}(M(x_m,x_n)-d(A,B))\le \underset{m,n\to \mathrm{\infty }}{lim}d(x_m,x_n).$$

(23)

On the other hand,

$$\begin{array}{rl}0& \le N(x_m,x_n)-d(A,B)\\ =min\{d(x_m,T{x}_m),d(x_n,T{x}_n),d(x_m,T{x}_n),d(x_n,T{x}_m)\}-d(A,B)\\ \le min\{d(x_m,x_{m+1})+d(A,B),d(x_n,T{x}_n),d(x_m,T{x}_n),d(x_n,T{x}_m)\}-d(A,B).\end{array}$$

(24)

Due to the fact that ${lim}_{n\to \mathrm{\infty }}d(x_n,x_{n+1})=0$, we obtain

$$\underset{m,n\to \mathrm{\infty }}{lim}[N(x_m,x_n)-d(A,B)]=0.$$

(25)

We shall show next that $\{x_n\}$ is a Cauchy sequence. Assume on the contrary that

$$\epsilon =\underset{m,n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}d(x_n,x_m)>0.$$

(26)

Employing the triangular inequality and (22), we get

$$\begin{array}{rl}d(x_n,x_m)& \le d(x_n,x_{n+1})+d(x_{n+1},x_{m+1})+d(x_{m+1},x_m)\\ \le d(x_n,x_{n+1})+d(T{x}_n,T{x}_m)+d(x_{m+1},x_m).\end{array}$$

(27)

Combining (10) and (27), and regarding the properties of ψ, we obtain

$$\begin{array}{rl}\psi (d(x_n,x_m))\le & \psi (d(x_n,x_{n+1})+d(T{x}_n,T{x}_m)+d(x_{m+1},x_m))\\ \le & \psi (d(x_n,x_{n+1}))+\psi (d(T{x}_n,T{x}_m))+\psi (d(x_{m+1},x_m))\\ \le & \psi (d(x_n,x_{n+1}))+\beta \left(\psi (M(x_n,x_m))\right)\psi (M(x_n,x_m)-d(A,B))\\ +L\psi (N(x_n,x_m)-d(A,B))+\psi (d(x_{m+1},x_m)).\end{array}$$

(28)

From (23), (25), (28), and by using ${lim}_{n\to \mathrm{\infty }}d(x_n,x_{n+1})=0$, we have

$$\begin{array}{rcl}\underset{m,n\to \mathrm{\infty }}{lim}\psi (d(x_n,x_m))& \le & \underset{m,n\to \mathrm{\infty }}{lim}\beta \left(\psi (M(x_n,x_m))\right)\underset{m,n\to \mathrm{\infty }}{lim}\psi (M(x_m,x_n)-d(A,B))\\ \le & \underset{m,n\to \mathrm{\infty }}{lim}\beta \left(\psi (M(x_n,x_m))\right)\underset{m,n\to \mathrm{\infty }}{lim}\psi (d(x_m,x_n)).\end{array}$$

So by (26), we get

$$1\le \underset{m,n\to \mathrm{\infty }}{lim}\beta \left(\psi (M(x_n,x_m))\right),$$

that is, ${lim}_{m,n\to \mathrm{\infty }}\beta (\psi (M(x_n,x_m)))=1$. Therefore, ${lim}_{m,n\to \mathrm{\infty }}M(x_n,x_m)=0$. This implies that ${lim}_{m,n\to \mathrm{\infty }}d(x_n,x_m)=0$, which is a contradiction. Therefore, $\{x_n\}$ is a Cauchy sequence.

Since $\{x_n\}\subset A$ and A is a closed subset of the complete metric space $(X,d)$, we can find $x^{\ast }\in A$ such that $x_n\to x^{\ast }$ as $n\to \mathrm{\infty }$. We shall show that $d(x^{\ast },T{x}^{\ast })=d(A,B)$. If $x^{\ast }=T{x}^{\ast }$, then $A\cap B\ne \mathrm{\varnothing }$, and $d(x^{\ast },T{x}^{\ast })=d(A,B)=0$, i.e., $x^{\ast }$ is a best proximity point of T. Hence, we assume that $d(x^{\ast },T{x}^{\ast })>0$. Suppose on the contrary that $x^{\ast }$ is not a best proximity point of T, that is, $d(x^{\ast },T{x}^{\ast })>d(A,B)$. First note that

$$\begin{array}{rl}d(x^{\ast },T{x}^{\ast })& \le d(x^{\ast },T{x}_n)+d(T{x}_n,T{x}^{\ast })\\ \le d(x^{\ast },x_{n+1})+d(x_{n+1},T{x}_n)+d(T{x}_n,T{x}^{\ast })\\ \le d(x^{\ast },x_{n+1})+d(A,B)+d(T{x}_n,T{x}^{\ast }).\end{array}$$

Taking the limit as $n\to \mathrm{\infty }$ in the above inequality, we obtain

$$d(x^{\ast },T{x}^{\ast })-d(A,B)\le \underset{n\to \mathrm{\infty }}{lim}d(T{x}_n,T{x}^{\ast }).$$

Since ψ is nondecreasing and continuous, then

$$\psi (d(x^{\ast },T{x}^{\ast })-d(A,B))\le \psi \left(\underset{n\to \mathrm{\infty }}{lim}d(T{x}_n,T{x}^{\ast })\right)=\underset{n\to \mathrm{\infty }}{lim}\psi \left(d(T{x}_n,T{x}^{\ast })\right).$$

(29)

Also, letting $n\to \mathrm{\infty }$ in (13) results in

$$\underset{n\to \mathrm{\infty }}{lim}d(x_n,T{x}_n)\le d(A,B),$$

that is, ${lim}_{n\to \mathrm{\infty }}d(x_n,T{x}_n)=d(A,B)$. Then we get

$$\underset{n\to \mathrm{\infty }}{lim}M(x_n,x^{\ast })=max\{\underset{n\to \mathrm{\infty }}{lim}d(x^{\ast },x_n),\underset{n\to \mathrm{\infty }}{lim}d(x_n,T{x}_n),d(x^{\ast },T{x}^{\ast })\}=d(x^{\ast },T{x}^{\ast }),$$

and therefore

$$\underset{n\to \mathrm{\infty }}{lim}\psi (M(x_n,x^{\ast })-d(A,B))=\psi (d(x^{\ast },T{x}^{\ast })-d(A,B)).$$

(30)

Further,

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}N(x_n,x^{\ast })-d(A,B)\\ =min\{\underset{n\to \mathrm{\infty }}{lim}d(x_n,T{x}_n),d(x^{\ast },T{x}^{\ast }),\underset{n\to \mathrm{\infty }}{lim}d(x_n,T{x}^{\ast }),\underset{n\to \mathrm{\infty }}{lim}d(x^{\ast },T{x}_n)\}-d(A,B),\end{array}$$

which implies

$$\underset{n\to \mathrm{\infty }}{lim}N(x_n,x^{\ast })-d(A,B)=0.$$

(31)

Therefore, combining (10), (29), (30), and (31) we deduce

$$\begin{array}{rl}\psi (d(x^{\ast },T{x}^{\ast })-d(A,B))\le & \underset{n\to \mathrm{\infty }}{lim}\psi \left(d(T{x}_n,T{x}^{\ast })\right)\\ \le & \underset{n\to \mathrm{\infty }}{lim}\beta \left(\psi \left(M(x_n,x^{\ast })\right)\right)\underset{n\to \mathrm{\infty }}{lim}\psi (M(x_n,x^{\ast })-d(A,B))\\ +L\underset{n\to \mathrm{\infty }}{lim}\psi (N(x_n,x^{\ast })-d(A,B))\\ =& \underset{n\to \mathrm{\infty }}{lim}\beta \left(\psi \left(M(x_n,x^{\ast })\right)\right)\psi (d(x^{\ast },T{x}^{\ast })-d(A,B)).\end{array}$$

(32)

Now, since $\psi (d(x^{\ast },T{x}^{\ast })-d(A,B))>0$, and making use of (32), we get

$$1\le \underset{n\to \mathrm{\infty }}{lim}\beta \left(\psi \left(M(x_n,x^{\ast })\right)\right),$$

that is,

$$\underset{n\to \mathrm{\infty }}{lim}\beta \left(\psi \left(M(x_n,x^{\ast })\right)\right)=1,$$

which implies

$$\underset{n\to \mathrm{\infty }}{lim}M(x_n,x^{\ast })=d(x^{\ast },T{x}^{\ast })=0,$$

and so $d(x^{\ast },T{x}^{\ast })=0>d(A,B)$, which is a contradiction. Therefore, $d(x^{\ast },T{x}^{\ast })\le d(A,B)$, that is, $d(x^{\ast },T{x}^{\ast })=d(A,B)$. In other words, $x^{\ast }$ is a best proximity point of T. This completes the proof of the existence of a best proximity point.

We shall show next the uniqueness of the best proximity point of T. Suppose that $x^{\ast }$ and $y^{\ast }$ are two best proximity points of T, such that $x^{\ast }\ne y^{\ast }$. This implies that

$$d(x^{\ast },T{x}^{\ast })=d(A,B)=d(y^{\ast },T{y}^{\ast }),$$

(33)

where $d(x^{\ast },y^{\ast })>0$. Due to the weak P-property of the pair $(A,B)$, we have

$$d(x^{\ast },y^{\ast })\le d(T{x}^{\ast },T{y}^{\ast }).$$

(34)

Observe that in this case

$$\begin{array}{rcl}M(x^{\ast },y^{\ast })& =& max\{d(x^{\ast },y^{\ast }),d(x^{\ast },T{x}^{\ast }),d(y^{\ast },T{y}^{\ast })\}\\ =& max\{d(x^{\ast },y^{\ast }),d(A,B),d(A,B)\}.\end{array}$$

Also, note that

$$\begin{array}{rcl}N(x^{\ast },y^{\ast })-d(A,B)& =& min\{d(x^{\ast },T{x}^{\ast }),d(y^{\ast },T{y}^{\ast }),d(x^{\ast },T{y}^{\ast }),d(y^{\ast },T{x}^{\ast })\}-d(A,B)\\ =& min\{d(A,B),d(A,B),d(x^{\ast },T{y}^{\ast }),d(y^{\ast },T{x}^{\ast })\}-d(A,B)\\ =& d(A,B)-d(A,B)=0.\end{array}$$

Using the fact that T is a generalized almost ψ-Geraghty contraction, we derive

$$\begin{array}{rcl}\psi \left(d(x^{\ast },y^{\ast })\right)& \le & \psi \left(d(T{x}^{\ast },T{y}^{\ast })\right)\\ \le & \beta \left(\psi \left(M(x^{\ast },y^{\ast })\right)\right)\psi (M(x^{\ast },y^{\ast })-d(A,B))+L\psi (N(x^{\ast },y^{\ast })-d(A,B))\\ =& \beta \left(\psi \left(M(x^{\ast },y^{\ast })\right)\right)\psi (M(x^{\ast },y^{\ast })-d(A,B))\\ <& \psi (M(x^{\ast },y^{\ast })-d(A,B)).\end{array}$$

If $M(x^{\ast },y^{\ast })=d(A,B)$, due to the fact that $d(x^{\ast },y^{\ast })>0$, the inequality above becomes

$$0<\psi \left(d(x^{\ast },y^{\ast })\right)<\psi (0),$$

(35)

which implies $d(x^{\ast },y^{\ast })=0$ and contradicts the assumption $d(x^{\ast },y^{\ast })>0$. Else, if $M(x^{\ast },y^{\ast })=d(x^{\ast },y^{\ast })$, we deduce

$$0<\psi \left(d(x^{\ast },y^{\ast })\right)<\psi (d(x^{\ast },y^{\ast })-d(A,B)),$$

(36)

which is not possible, since ψ is nondecreasing. Therefore, we must have $d(x^{\ast },y^{\ast })=0$. This completes the proof. □

To illustrate our result given in Theorem 2.1, we present the following example, which shows that Theorem 2.1 is a proper generalization of Theorem 1.2.

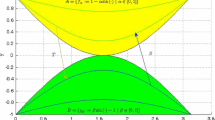
Example 2.1 Consider the space $X=\mathbb{R}$ with Euclidean metric. Take the sets

$$A=(-\mathrm{\infty },-1]\text{and}B=[1,+\mathrm{\infty }).$$

Obviously, $d(A,B)=2$. Let $T:A\to B$ be defined by $Tx=-x$. Notice that $A_0=\{-1\}$, $B_0=\{1\}$ and $T(A_0)\subseteq B_0$. Also, it is clear that the pair $(A,B)$ has the weak P-property.

Consider

$$\beta (t)=\{\begin{array}{ll}\frac{1}{1+t},& \text{if }0\le t<1,\\ \frac{t}{1+t},& \text{if }t\ge 1,\end{array}$$

and $\psi (t)=\alpha t$ (with $\alpha \ge \frac{1}{2}$) for all $t\ge 0$. Note that $\beta \in S$ and $\psi \in \mathrm{\Psi }$. For all $x,y\in A$, we have

$$d(Tx,Ty)=|x-y|\text{and}M(x,y)=max\{|x-y|,-2x,-2y\}.$$

We shall show that T is a generalized almost ψ-Geraghty contraction. Without loss of generality, consider the case where $x\ge y$. Then we have $M(x,y)=-2y$ and $d(Tx,Ty)=x-y$.

In this case, we see that

$$\begin{array}{rl}\psi (d(Tx,Ty))& =\alpha (x-y)\le \alpha (-x-y-2)\\ \le 2{\alpha }^2(-x-y-2)\le [-2\alpha y][\alpha (-x-y-2)]\\ =[-2\alpha y][\alpha (-2y-2)-\alpha (x-y)]\\ =\psi (M(x,y))[\psi (M(x,y)-d(A,B))-\psi (d(Tx,Ty))].\end{array}$$

Therefore

$$\psi (d(Tx,Ty))\le \frac{\psi (M(x,y))}{1+\psi (M(x,y))}\psi (M(x,y)-d(A,B)).$$

(37)

On the other hand, we know that $\psi (M(x,y))=-2\alpha y\ge 1$ for all $x,y\in A$ with $x\ge y$. Hence,

$$\beta \left(\psi (M(x,y))\right)=\frac{\psi (M(x,y))}{1+\psi (M(x,y))},$$

and from (37) we deduce

$$\psi (d(Tx,Ty))\le \beta \left(\psi (M(x,y))\right)\psi (M(x,y)-d(A,B)).$$

Thus, all hypotheses of Theorem 2.1 are satisfied, and $x^{\ast }=-1$ is the unique best proximity point of the map T.

On the other hand, T is not a Geraghty contraction. Indeed, taking $x=-1$ and $y=-2$, we get

$$d(Tx,Ty)=1>\frac{1}{2}=\beta (d(x,y))d(x,y).$$

Then Theorem 1.2 (the main result of Caballero et al. [6]) is not applicable.

Similarly, we cannot apply Theorem 1.3 because T is not a ψ-Geraghty contraction. Let $x=-1$, $y=-2$ and $\psi (t)=\alpha t$ with $\alpha <2$. Then T does not satisfy (8).

If in Theorem 2.1 we take $\psi (t)=t$ for all $t\ge 0$, then we deduce the following corollary.

Corollary 2.1 Let $(A,B)$ be a pair of nonempty closed subsets of a complete metric space $(X,d)$ such that $A_0$ is nonempty. Let $T:A\to B$ be a non-self-mapping satisfying $T(A_0)\subseteq B_0$ and

$$d(Tx,Ty)\le \beta (M(x,y))[M(x,y)-d(A,B)]+L[N(x,y)-d(A,B)]$$

for all $x,y\in A$ where $\beta \in S$, $L\ge 0$,

$$\begin{array}{c}M(x,y)=max\{d(x,y),d(x,Tx),d(y,Ty)\},\hfill \\ N(x,y)=min\{d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)\}.\hfill \end{array}$$

Assume that the pair $(A,B)$ has the weak P-property. Then T has a unique best proximity point in A.

If further in the above corollary we take $\beta (t)=r$ where $0\le r<1$, then we deduce another particular result.

Corollary 2.2 Let $(A,B)$ be a pair of nonempty closed subsets of a complete metric space $(X,d)$ such that $A_0$ is nonempty. Let $T:A\to B$ be a non-self-mapping satisfying $T(A_0)\subseteq B_0$ and

$$d(Tx,Ty)\le r[M(x,y)-d(A,B)]+L[N(x,y)-d(A,B)]$$

for all $x,y\in A$ where $0\le r<1$, $L\ge 0$,

$$\begin{array}{c}M(x,y)=max\{d(x,y),d(x,Tx),d(y,Ty)\},\hfill \\ N(x,y)=min\{d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)\}.\hfill \end{array}$$

Assume that the pair $(A,B)$ has the weak P-property. Then T has a unique best proximity point in A.

3 Application to fixed point theory

The case $A=B$ in Theorem 2.1 corresponds to a self-mapping and results in an existence and uniqueness theorem for a fixed point of the map T. We state this case in the next theorem.

Theorem 3.1 Let $(X,d)$ be a complete metric space. Suppose that A is a nonempty closed subset of X. Let $T:A\to A$ be a mapping such that

$$\psi (d(Tx,Ty))\le \beta \left(\psi (M(x,y))\right)\psi (M(x,y))+L\psi (N(x,y))\mathit{\text{for any }}x,y\in A,$$

(38)

where $\psi \in \mathrm{\Psi }$, $\beta \in S$, $L\ge 0$,

$$\begin{array}{c}M(x,y)=max\{d(x,y),d(x,Tx),d(y,Ty)\}\mathit{\text{and}}\hfill \\ N(x,y)=min\{d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)\}.\hfill \end{array}$$

Then T has a unique fixed point.

Finally, taking $\psi (t)=t$ in Theorem 3.1, we get another fixed point result.

Corollary 3.1 Let $(X,d)$ be a complete metric space. Suppose that A is a nonempty closed subset of X. Let $T:A\to A$ be a mapping such that

$$d(Tx,Ty)\le \beta (M(x,y))M(x,y)+LN(x,y)\mathit{\text{for any }}x,y\in A,$$

(39)

where $\beta \in S$, $L\ge 0$,

$$\begin{array}{c}M(x,y)=max\{d(x,y),d(x,Tx),d(y,Ty)\}\mathit{\text{and}}\hfill \\ N(x,y)=min\{d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)\}.\hfill \end{array}$$

Then T has a unique fixed point.

Remark 3.1 The best proximity theorem given in this work, more precisely Theorem 2.1, is a quite general result. It is a generalization of Theorem 2.1 in [14], Theorem 8 in [5], and also Theorem 1.2 given in Section 1. In addition, Corollary 3.1 improves Theorem 1.1.

Remark 3.2 Very recently, Karapınar and Samet [15] proved that the function $d_{\phi }=\phi \circ d$ on the set X, where $\phi \in \mathrm{\Psi }$ is also a metric on X. Therefore, some of the fixed theorems regarding contraction mappings defined via auxiliary functions from the set Ψ can be in fact deduced from the existing ones in the literature. However, our main result given in Theorem 2.1 is not a consequence of any existing theorems due to the fact that the contraction condition contains the term $d(A,B)$.

On the other hand, the definition of $d_{\phi }=\phi \circ d$ can be used to show that Theorem 3.1 follows from Corollary 3.1. Nevertheless, Corollary 3.1 and hence Theorem 3.1 are still new results.