Strong convergence theorem for quasi-Bregman strictly pseudocontractive mappings and equilibrium problems in Banach spaces

Abstract

In this paper, we introduce a new iterative scheme by a hybrid method and prove a strong convergence theorem of a common element in the set of fixed points of a finite family of closed quasi-Bregman strictly pseudocontractive mappings and common solutions to a system of equilibrium problems in reflexive Banach space. Our results extend important recent results announced by many authors.

MSC:47H09, 47J25.

1 Introduction

Let E be a real Banach space and C a nonempty closed convex subset of E. The normalized duality map from E to $2^{E^{\ast }}$ ($E^{\ast }$ is the dual space of E) denoted by J is defined by

$$J(x)=\{f\in E^{\ast }:〈x,f〉={\parallel x\parallel }^2={\parallel f\parallel }^2\}.$$

Let $T:C\to C$ be a map, a point $x\in C$ is called a fixed point of T if $Tx=x$, and the set of all fixed points of T is denoted by $F(T)$. The mapping T is called L-Lipschitzian or simply Lipschitz if there exists $L>0$, such that $\parallel Tx-Ty\parallel \le L\parallel x-y\parallel$, $\mathrm{\forall }x,y\in C$ and if $L=1$, then the map T is called nonexpansive.

Let $g:C\times C\to \mathbb{R}$ be a bifunction. The equilibrium problem with respect to g is to find

$$z\in C\text{ such that }g(z,y)\ge 0,\mathrm{\forall }y\in C.$$

The set of solution of equilibrium problem is denoted by $EP(g)$. Thus

$$EP(g):=\{z\in C:g(z,y)\ge 0,\mathrm{\forall }y\in C\}.$$

Numerous problems in physics, optimization and economics reduce to finding a solution of equilibrium problem. Some methods have been proposed to solve the equilibrium problem in Hilbert spaces; see for example Blum and Oettli [1], Combettes and Hirstoaga [2]. Recently, Tada and Takahashi [3, 4] and Takahashi and Takahashi [5] obtain weak and strong convergence theorems for finding a common element of the set of solutions of an equilibrium problem and set of fixed points of a nonexpansive mapping in Hilbert space. In particular, Takahashi and Zembayashi [4] established a strong convergence theorem for finding a common element of the two sets by using the hybrid method introduced in Nakajo and Takahashi [6]. They also proved such a strong convergence theorem in a uniformly convex and uniformly smooth Banach space.

Reich and Sabach [7] and Kassay et al. [8] proved some convergence theorems for the solution of some equilibrium and variational inequality problems in the setting of reflexive Banach spaces.

Let $\varphi :E\times E\to [0,\mathrm{\infty })$ denote the Lyapunov functional defined by

$$\varphi (x,y)={\parallel x\parallel }^2-2〈x,Jy〉+{\parallel y\parallel }^2,\mathrm{\forall }x,y\in E.$$

A mapping $T:C\to C$ is said to be quasi-ϕ strictly pseudocontractive, see [9], if $F(T)\ne \mathrm{\varnothing }$ and there exists a constant $k\in (0,1]$ such that

$$\varphi (p,Tx)\le \varphi (p,x)+k\varphi (x,Tx),\mathrm{\forall }x\in C\text{ and }p\in F(T).$$

Let E be a real reflexive Banach space with norm $\parallel \cdot \parallel$ and $E^{\ast }$ the dual space of E. Throughout this paper, we shall assume $f:E\to (-\mathrm{\infty },+\mathrm{\infty }]$ is a proper, lower semi-continuous and convex function. We denote by $domf:=\{x\in E:f(x)<+\mathrm{\infty }\}$ the domain of f.

Let $x\in intdomf$; the subdifferential of f at x is the convex set defined by

$$\partial f(x)=\{x^{\ast }\in E^{\ast }:f(x)+〈x^{\ast },y-x〉\le f(y),\mathrm{\forall }y\in E\},$$

where the Fenchel conjugate of f is the function $f^{\ast }:E^{\ast }\to (-\mathrm{\infty },+\mathrm{\infty }]$ defined by

$$f^{\ast }\left(x^{\ast }\right)=sup\{〈x^{\ast },x〉-f(x):x\in E\}.$$

We know that the Young-Fenchel inequality holds:

$$〈x^{\ast },x〉\le f(x)+f^{\ast }\left(x^{\ast }\right),\mathrm{\forall }x\in E,x^{\ast }\in E^{\ast }.$$

A function f on E is coercive [10] if the sublevel set of f is bounded; equivalently,

$$\underset{\parallel x\parallel \to +\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty }.$$

A function f on E is said be strongly coercive [11] if

$$\underset{\parallel x\parallel \to +\mathrm{\infty }}{lim}\frac{f(x)}{\parallel x\parallel }=+\mathrm{\infty }.$$

For any $x\in intdomf$ and $y\in E$, the right-hand derivative of f at x in the direction y is defined by

$$f^{\circ }(x,y):=\underset{t\to 0^{+}}{lim}\frac{f(x+ty)-f(x)}{t}.$$

The function f is said to be Gâteaux differentiable at x if ${lim}_{t\to 0^{+}}\frac{f(x+ty)-f(x)}{t}$ exists for any y. In this case, $f^{\circ }(x,y)$ coincides with $\mathrm{\nabla }f(x)$, the value of the gradient ∇f of f at x. The function f is said to be Gâteaux differentiable if it is Gâteaux differentiable for any $x\in intdomf$. The function f is said to be Fréchet differentiable at x if this limit is attained uniformly in $\parallel y\parallel =1$. Finally, f is said to be uniformly Fréchet differentiable on a subset C of E if the limit is attained uniformly for $x\in C$ and $\parallel y\parallel =1$. It is well known that if f is Gâteaux differentiable (resp. Fréchet differentiable) on $intdomf$, then f is continuous and its Gâteaux derivative ∇f is norm-to-weak^∗ continuous (resp. continuous) on $intdomf$ (see also [12, 13]). We will need the following results.

Lemma 1.1 [14]

If $f:E\to \mathbb{R}$ is uniformly Fréchet differentiable and bounded on bounded subsets of E, then ∇f is uniformly continuous on bounded subsets of E from the strong topology of E to the strong topology of $E^{\ast }$.

Definition 1.2 [15]

The function f is said to be:

• (i) essentially smooth, if ∂f is both locally bounded and single-valued on its domain;

• (ii) essentially strictly convex, if ${(\partial f)}^{-1}$ is locally bounded on its domain and f is strictly convex on every convex subset of $dom\partial f$;

• (iii) Legendre, if it is both essentially smooth and essentially strictly convex.

Remark 1.3 Let E be a reflexive Banach space. Then we have:

• (i) f is essentially smooth if and only if $f^{\ast }$ is essentially strictly convex (see [15], Theorem 5.4);

• (ii) ${(\partial f)}^{-1}=\partial f^{\ast }$ (see [13]);

• (iii) f is Legendre if and only if $f^{\ast }$ is Legendre (see [15], Corollary 5.5);

• (iv) if f is Legendre, then ∇f is a bijection satisfying $\mathrm{\nabla }f={(\mathrm{\nabla }{f}^{\ast })}^{-1}$, $ran\mathrm{\nabla }f=dom\mathrm{\nabla }{f}^{\ast }=intdom{f}^{\ast }$ and $ran\mathrm{\nabla }{f}^{\ast }=domf=intdomf$ (see [15], Theorem 5.10).

Examples of Legendre functions were given in [15, 16]. One important and interesting Legendre function is $\frac{1}{p}{\parallel \cdot \parallel }^p$ ($1<p<\mathrm{\infty }$) when E is a smooth and strictly convex Banach space. In this case the gradient ∇f of f is coincident with the generalized duality mapping of E, i.e., $\mathrm{\nabla }f=J_p$ ($1<p<\mathrm{\infty }$). In particular, $\mathrm{\nabla }f=I$ the identity mapping in Hilbert spaces. In the rest of this paper, we always assume that $f:E\to (-\mathrm{\infty },+\mathrm{\infty }]$ is Legendre.

Let $f:E\to (-\mathrm{\infty },+\mathrm{\infty }]$ be a convex and Gâteaux differentiable function. The function $D_f:domf\times intdomf\to [0,+\mathrm{\infty })$, defined as follows:

$$D_f(y,x):=f(y)-f(x)-〈\mathrm{\nabla }f(x),y-x〉,$$

(1.1)

is called the Bregman distance with respect to f (see [17]). It is obvious from the definition of $D_f$ that

$$D_f(z,x)=D_f(z,y)+D_f(y,x)+〈\mathrm{\nabla }f(y)-\mathrm{\nabla }f(x),z-y〉.$$

(1.2)

Recall that the Bregman projection [18] of $x\in intdomf$ onto the nonempty, closed, and convex set $C\subset domf$ is the necessarily unique vector $P_C^f(x)\in C$ satisfying

$$D_f(P_C^f(x),x)=inf\{D_f(y,x):y\in C\}.$$

Concerning the Bregman projection, the following are well known.

Lemma 1.4 [19]

Let C be a nonempty, closed, and convex subset of a reflexive Banach space E. Let $f:E\to \mathbb{R}$ be a Gâteaux differentiable and totally convex function and let $x\in E$. Then:

• (a) $z=P_C^f(x)$ if and only if $〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(z),y-z〉\le 0$, $\mathrm{\forall }y\in C$;

• (b) $D_f(y,P_C^f(x))+D_f(P_C^f(x),x)\le D_f(y,x)$, $\mathrm{\forall }x\in E$, $y\in C$.

Let $f:E\to (-\mathrm{\infty },+\mathrm{\infty }]$ be a convex and Gâteaux differentiable function. The modulus of the total convexity of f at $x\in intdomf$ is the function $v_f(x,\cdot ):[0,+\mathrm{\infty })\to [0,+\mathrm{\infty }]$ defined by

$$v_f(x,t):=inf\{D_f(y,x):y\in domf,\parallel y-x\parallel =t\}.$$

The function f is called totally convex at x if $v_f(x,t)>0$ whenever $t>0$. The function f is called totally convex if it is totally convex at any point $x\in intdomf$ and is said to be totally convex on bounded sets if $v_f(B,t)>0$ for any nonempty bounded subset B of E and $t>0$, where the modulus of the total convexity of the function f on the set B is the function $v_f:intdomf\times [0,+\mathrm{\infty })\to [0,+\mathrm{\infty }]$ defined by

$$v_f(B,t):=inf\{v_f(x,t):x\in B\cap domf\}.$$

Lemma 1.5 [20]

If $x\in domf$, then the following statements are equivalent:

• (i) the function f is totally convex at x;

• (ii) for any sequence $\{y_n\}\subset domf$,

  $$\underset{n\to +\mathrm{\infty }}{lim}{D}_f(y_n,x)=0\Rightarrow \underset{n\to +\mathrm{\infty }}{lim}\parallel y_n-x\parallel =0.$$

Recall that the function f called sequentially consistent [19] if for any two sequences $\{x_n\}$ and $\{y_n\}$ in E such that the first one is bounded

$$\underset{n\to +\mathrm{\infty }}{lim}{D}_f(y_n,x_n)=0\Rightarrow \underset{n\to +\mathrm{\infty }}{lim}\parallel y_n-x_n\parallel =0.$$

Lemma 1.6 [21]

The function f is totally convex on bounded sets if and only if the function f is sequentially consistent.

Lemma 1.7 [22]

Let $f:E\to \mathbb{R}$ be a Gâteaux differentiable and totally convex function. If $x_0\in E$ and the sequence $\{D_f(x_n,x_0)\}$ is bounded, then the sequence $\{x_n\}$ is bounded too.

Lemma 1.8 [22]

Let $f:E\to \mathbb{R}$ be a Gâteaux differentiable and totally convex function, $x_0\in E$ and let C be a nonempty, closed, and convex subset of E. Suppose that the sequence $\{x_n\}$ is bounded and any weak subsequential limit of $\{x_n\}$ belongs to C. If $D_f(x_n,x_0)\le D_f(P_C^f(x_0),x_0)$ for any $n\in \mathbb{R}$, then $\{x_n\}$ converges strongly to $P_C^f(x_0)$.

A mapping T is said to be Bregman firmly nonexpansive [23], if for all $x,y\in C$,

$$〈\mathrm{\nabla }f(Tx)-\mathrm{\nabla }f(Ty),Tx-Ty〉\le 〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(y),Tx-Ty〉$$

or, equivalently,

$$D_f(Tx,Ty)+D_f(Ty,Tx)+D_f(Tx,x)+D_f(Ty,y)\le D_f(Tx,y)+D_f(Ty,x).$$

A point $p\in C$ is said to be asymptotic fixed point of a map T, if there exists a sequence $\{x_n\}$ in C which converges weakly to p such that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$. We denote by $\hat{F}(T)$ the set of asymptotic fixed points of T. A point $p\in C$ is said to be strong asymptotic fixed point of a map T, if there exists a sequence $\{x_n\}$ in C which converges strongly to p such that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$. We denote by $\tilde{F}(T)$ the set of strong asymptotic fixed points of T. Let $f:E\to \mathbb{R}$, a mapping $T:C\to C$ is said to be Bregman relatively nonexpansive [24] if $F(T)\ne \mathrm{\varnothing }$, $\hat{F}(T)=F(T)$ and $D_f(p,T(x))\le D_f(p,x)$ for all $x\in C$ and $p\in F(T)$. The map $T:C\to C$ is said to be Bregman weak relatively nonexpansive if $F(T)\ne \mathrm{\varnothing }$, $\tilde{F}(T)=F(T)$ and $D_f(p,T(x))\le D_f(p,x)$ for all $x\in C$ and $p\in F(T)$. T is said to be quasi-Bregman relatively nonexpansive if $F(T)\ne \mathrm{\varnothing }$, and $D_f(p,T(x))\le D_f(p,x)$ for all $x\in C$ and $p\in F(T)$. In [22] quasi-Bregman relatively nonexpansive is called left quasi-Bregman relatively nonexpansive. A map $T:C\to C$ is called right quasi-Bregman relatively nonexpansive [25] if $F(T)\ne \mathrm{\varnothing }$, and $D_f(T(x),p)\le D_f(x,p)$ for all $x\in C$ and $p\in F(T)$. T is said to be quasi-Bregman strictly pseudocontractive if there exist a constant $k\in [0,1)$ and $F(T)\ne \mathrm{\varnothing }$ such that $D_f(p,Tx)\le D_f(p,x)+k{D}_f(x,Tx)$ for all $x\in C$ and $p\in F(T)$. In particular, T is said to be quasi-Bregman relatively nonexpansive if $k=0$ and T is said to be quasi-Bregman pseudocontractive if $k=1$.

Very recently, Zhou and Gao [9] introduced this definition of a quasi-strict pseudocontraction related to the function ϕ and proved the convergence of a hybrid projection algorithm to a fixed point of a closed and quasi-strict pseudocontraction in a smooth and uniformly convex Banach space. They studied the strong convergence of the following scheme:

$$\{\begin{array}{l}{x}_0\in E,\\ C_1=C,\\ x_1={\prod }_{C_1}(x_0),\\ C_{n+1}=\{z\in C_n:\varphi (x_n,T{x}_n)\le \frac{2}{1-k}〈x_n-z,J{x}_n-JT{x}_n〉\},\\ x_{n+1}={\prod }_{C_{n+1}}(x_0),\end{array}$$

where ${\prod }_{C_{n+1}}$ is the generalized projection from E onto $C_{n+1}$. They proved that the sequence $\{x_n\}$ converges strongly to ${\prod }_{F(T)}(x_0)$.

Recently, Zegeye and Shahzad [26] proved a strong convergence theorem for the common fixed point of a finite family of right Bregman strongly nonexpansive mappings in a reflexive Banach space. Alghamdi et al. [27] proved a strong convergence theorem for the common fixed point of a finite family of quasi-Bregman nonexpansive mappings. Pang et al. [28] proved weak convergence theorems for Bregman relatively nonexpansive mappings. Shahzad and Zegeye [29] proved a strong convergence theorem for multivalued Bregman relatively nonexpansive mappings, while Zegeye and Shahzad [30] proved a strong convergence theorem for a finite family of Bregman weak relatively nonexpansive mappings.

Motivated and inspired by the above works, in this paper, we prove a new strong convergence theorem for a finite family of closed quasi-Bregman strictly pseudocontractive mapping and a system of equilibrium problems in a real reflexive Banach space. These results generalize and improve several recent results. We showed by an example that the class of quasi-Bregman strictly pseudocontractive mappings is a proper generalization of the class of quasi-ϕ-Bregman strictly pseudocontractive mappings.

2 Preliminaries

The next lemma will be useful in the proof of our main results.

Lemma 2.1 Let $f:E\to \mathbb{R}$ be a Legendre function which is uniformly Fréchet differentiable and bounded on subsets of E, let C be a nonempty, closed, and convex subset of E and let $T:C\to C$ be a quasi-Bregman strictly pseudocontractive mapping with respect to f. Then, for any $x\in C$, $p\in F(T)$ and $k\in [0,1)$ the following hold:

$$D_f(x,Tx)\le \frac{1}{1-k}〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(Tx),x-p〉.$$

(2.1)

Proof Let $x\in C$, $p\in F(T)$ and $k\in [0,1)$, by definition of T, we have

$$D_f(p,Tx)\le D_f(p,x)+k{D}_f(x,Tx)$$

and, from (1.2), we obtain

$$D_f(p,x)+D_f(x,Tx)+〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(Tx),p-x〉\le D_f(p,x)+k{D}_f(x,Tx),$$

which implies

$$D_f(x,Tx)\le \frac{1}{1-k}〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(Tx),x-p〉.$$

This completes the proof. □

Lemma 2.2 [31]

Let E be a real reflexive Banach space, $f:E\to (-\mathrm{\infty },+\mathrm{\infty }]$ be a proper lower semi-continuous function, then $f^{\ast }:E^{\ast }\to (-\mathrm{\infty },+\mathrm{\infty }]$ is a proper weak ^∗ lower semi-continuous and convex function. Thus, for all $z\in E$, we have

$$D_f(z,\mathrm{\nabla }{f}^{\ast }(\sum _{i=1}^N{t}_i\mathrm{\nabla }f(x_i)))\le \sum _{i=1}^N{t}_i{D}_f(z,x_i).$$

(2.2)

In order to solve the equilibrium problem, let us assume that a bifunction $g:C\times C\to \mathbb{R}$ satisfies the following conditions [1]:

(A1) $g(x,x)=0$, $\mathrm{\forall }x\in C$;

(A2) g is monotone, i.e., $g(x,y)+g(y,x)\le 0$, $\mathrm{\forall }x,y\in C$;

(A3) ${lim\hspace{0.17em}sup}_{t\downarrow 0}g(x+t(z-x),y)\le g(x,y)$, $\mathrm{\forall }x,z,y\in C$;

(A4) the function $y\mapsto g(x,y)$ is convex and lower semi-continuous.

The resolvent of a bifunction g [2] is the operator ${Res}_g^f:E\to 2^C$ defined by

$${Res}_g^f(x)=\{z\in C:g(z,y)+〈\mathrm{\nabla }f(z)-\mathrm{\nabla }f(x),y-z〉\ge 0,\mathrm{\forall }y\in C\}.$$

(2.3)

From Lemma 1, in [32], if $f:(-\mathrm{\infty },+\mathrm{\infty }]\to \mathbb{R}$ is a strongly coercive and Gâteaux differentiable function, and g satisfies conditions (A1)-(A4), then $dom({Res}_g^f)=E$. The following lemma gives some characterization of the resolvent ${Res}_g^f$.

Lemma 2.3 [32]

Let E be a real reflexive Banach space and C be a nonempty closed convex subset of E. Let $f:E\to (-\mathrm{\infty },+\mathrm{\infty }]$ be a Legendre function. If the bifunction $g:C\times C\to \mathbb{R}$ satisfies the conditions (A1)-(A4), then the following hold:

• (i) ${Res}_g^f$ is single-valued;

• (ii) ${Res}_g^f$ is a Bregman firmly nonexpansive operator;

• (iii) $F({Res}_g^f)=EP(g)$;

• (iv) $EP(g)$ is closed and convex subset of C;

• (v) for all $x\in E$ and for all $q\in F({Res}_g^f)$, we have

  $$D_f(q,{Res}_g^f(x))+D_f({Res}_g^f(x),x)\le D_f(q,x).$$

  (2.4)

3 Main result

Lemma 3.1 Let $f:E\to \mathbb{R}$ be a Legendre function which is uniformly Fréchet differentiable on bounded subsets of E, let C be a nonempty, closed, and convex subset of E and let $T:C\to C$ be a quasi-Bregman strictly pseudocontractive mapping with respect to f. Then $F(T)$ is closed and convex.

Proof Let $F(T)$ be nonempty set. First we show that $F(T)$ is closed. Let $\{x_n\}$ be a sequence in $F(T)$ such that $x_n\to z$ as $n\to \mathrm{\infty }$, we need to show that $z\in F(T)$. From Lemma 2.1, we obtain

$$D_f(z,Tz)\le \frac{1}{1-k}〈\mathrm{\nabla }f(z)-\mathrm{\nabla }f(Tz),z-x_n〉.$$

(3.1)

From (3.1), we have $D_f(z,Tz)\le 0$, and from [15], Lemma 7.3, it follows that $Tz=z$. Therefore $F(T)$ is closed.

Next, we show that $F(T)$ is convex. Let $z_1,z_2\in F(T)$, for any $t\in (0,1)$; putting $z=t{z}_1+(1-t)z_2$, we need to show that $z\in F(T)$. From Lemma 2.1, we obtain, respectively,

$$D_f(z,Tz)\le \frac{1}{1-k}〈\mathrm{\nabla }f(z)-\mathrm{\nabla }f(Tz),z-z_1〉$$

(3.2)

and

$$D_f(z,Tz)\le \frac{1}{1-k}〈\mathrm{\nabla }f(z)-\mathrm{\nabla }f(Tz),z-z_2〉.$$

(3.3)

Multiplying (3.2) by t and (3.3) by $(1-t)$ and adding the results, we obtain

$$D_f(z,Tz)\le \frac{1}{1-k}〈\mathrm{\nabla }f(z)-\mathrm{\nabla }f(Tz),z-z〉,$$

(3.4)

which implies $D_f(z,Tz)\le 0$, and from [15], Lemma 7.3, it follows that $Tz=z$. Therefore $F(T)$ is also convex. This completes the proof. □

We now prove the following theorem.

Theorem 3.2 Let C be a nonempty, closed, and convex subset of a real reflexive Banach space E and $f:E\to \mathbb{R}$ a strongly coercive Legendre function which is bounded, uniformly Fréchet differentiable and totally convex on bounded subset of E. For each $k=1,2,\dots ,m$, let $g_k$ be a bifunction from $C\times C$ to ℝ satisfying (A1)-(A4) and let $\{T_{i=1}^N\}$ be a finite family of $L_i$-Lipschitzian, $i=1,2,3,\dots ,N$, closed and quasi-Bregman strictly pseudocontractive self mappings of C such that $F:=({\bigcap }_{k=1}^{m}EP(g_k))\cap ({\bigcap }_{i=1}^{N}F(T_i))\ne \mathrm{\varnothing }$. Let ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ be a sequence generated by $x_1=x\in C$, $C_1=C$ and

$$\{\begin{array}{l}{x}_1\in C,\\ y_n=\mathrm{\nabla }{f}^{\ast }({\alpha }_n\mathrm{\nabla }f(x_n)+(1-{\alpha }_n)\mathrm{\nabla }f(T_n{x}_n)),\\ u_{j,n}={Res}_{g_j}^f{y}_n,j=1,2,3,\dots ,m,\\ w_n=\mathrm{\nabla }{f}^{\ast }({\sum }_{j=1}^m{\beta }_{j,n}\mathrm{\nabla }f(u_{j,n})),\\ C_{n+1}=\{w\in C_n:D_f(x_n,w_n)\le \frac{1}{1-k}〈\mathrm{\nabla }f(x_n)\\ \phantom{C_{n+1}=}-\mathrm{\nabla }f(T_n{x}_n),x_n-w〉+〈\mathrm{\nabla }f(T_n{x}_n)-\mathrm{\nabla }f(w_n),x_n-w〉\},\\ x_{n+1}=P_{C_{n+1}}^f(x),n\in \mathbb{N},\end{array}$$

(3.5)

where $T_n=T_{n(modN)}$, and $k\in [0,1)$, for each $i=1,2,\dots ,N$, $T_i$ is uniformly continuous; suppose ${\{{\alpha }_n\}}_{n=1}^{\mathrm{\infty }}$ and ${\{{\beta }_{j,n}\}}_{n=1}^{\mathrm{\infty }}$, $j=1,2,\dots ,m$ are sequences in $(0,1)$ such that (i) ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}(1-{\alpha }_n)>0$, (ii) ${\sum }_{j=1}^m{\beta }_{j,n}=1$, $n\ge 1$. Then ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$ converges strongly to $P_F^f(x)$, where $P_F^f$ is the Bregman projection of E onto F.

Proof The proof is divided into six steps.

Step I. Show that $F=({\bigcap }_{j=1}^{m}EP(g_j))\cap ({\bigcap }_{i=1}^{N}F(T_i))$ is closed and convex. From Lemma 3.1, ${\bigcap }_{i=1}^{N}F(T_i)$ is closed and convex and from (iv) of Lemma 2.3, ${\bigcap }_{j=1}^{m}EP(g_j)$ is closed and convex. So, $F=({\bigcap }_{j=1}^{m}EP(g_j))\cap ({\bigcap }_{i=1}^{N}F(T_i))$ is closed and convex.

Step II. Show that $C_n$ is closed and convex for all $n\ge 1$. For $n=1$, $C_1=C$ is closed and convex. Assume that $C_h$ is closed and convex for some $h>1$. For $w\in C_{h+1}$, one obtains

$$\begin{array}{rcl}{D}_f(x_h,w_h)& \le & \frac{1}{1-k}〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉\\ +〈\mathrm{\nabla }f(T_h{x}_h)-\mathrm{\nabla }f(w_h),x_h-w〉;\end{array}$$

using the fact that $〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),\cdot 〉$ and $〈\mathrm{\nabla }f(T_h{x}_h)-\mathrm{\nabla }f(w_h),\cdot 〉$ are continuous and linear in E, for $h\ge 1$, $C_{h+1}$ is closed and convex.

Step III. Show that $F\subset C_n$ for every $n\ge 1$. Note that $F\subset C_1=C$. Suppose $F\subset C_h$, for $h\ge 1$, then for all $w\in F\subset C_h$, since $u_{j,h}={Res}_{g_j}^f(y_h)$ for each $j=1,2,\dots ,m$, from (2.2) and Lemma 2.3, we have

$$\begin{array}{rcl}{D}_f(w,w_h)& =& D_f(w,\mathrm{\nabla }{f}^{\ast }(\sum _{j=1}^m{\beta }_{j,n}\mathrm{\nabla }f(u_{j,n})))\\ \le & \sum _{j=1}^m{\beta }_{jh}{D}_f(w,u_{jh})\\ \le & \sum _{j=1}^m{\beta }_{jh}{D}_f(w,y_h)\\ =& D_f(w,y_h);\end{array}$$

(3.6)

also from (2.2) and (2.1), we obtain

$$\begin{array}{rcl}{D}_f(w,y_h)& =& D_f(w,\mathrm{\nabla }{f}^{\ast }({\alpha }_h\mathrm{\nabla }f(x_h)+(1-{\alpha }_h)\mathrm{\nabla }f(T_h{x}_h)))\\ \le & {\alpha }_h{D}_f(w,x_h)+(1-{\alpha }_h)D_f(w,T_h{x}_h)\\ \le & {\alpha }_h{D}_f(w,x_h)+(1-{\alpha }_h)[D_f(w,x_h)+k{D}_f(x_h,T_h{x}_h)]\\ \le & D_f(w,x_h)+k{D}_f(x_h,T_h{x}_h)\\ \le & D_f(w,x_h)+\frac{k}{1-k}〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉.\end{array}$$

(3.7)

But, from (1.2),

$$D_f(w,w_h)=D_f(w,x_h)+D_f(x_h,w_h)+〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(w_h),w-x_h〉.$$

(3.8)

From (3.6), (3.7), and (3.8), we obtain

$$\begin{array}{rcl}{D}_f(x_h,w_h)& \le & \frac{k}{1-k}〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉\\ +〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(w_h),x_h-w〉\\ =& \frac{k}{1-k}〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉\\ +〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉\\ +〈\mathrm{\nabla }f(T_h{x}_h)-\mathrm{\nabla }f(w_h),x_h-w〉\\ =& (\frac{k}{1-k}+1)〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉\\ +〈\mathrm{\nabla }f(T_h{x}_h)-\mathrm{\nabla }f(w_h),x_h-w〉\\ =& \frac{1}{1-k}〈\mathrm{\nabla }f(x_h)-\mathrm{\nabla }f(T_h{x}_h),x_h-w〉\\ +〈\mathrm{\nabla }f(T_h{x}_h)-\mathrm{\nabla }f(w_h),x_h-w〉.\end{array}$$

(3.9)

This shows that $w\in C_{h+1}$, which implies $F\subset C_n$ for every $n\ge 1$.

Step IV. Show that ${lim}_{n\to \mathrm{\infty }}{D}_f(x_n,x)$ exists. From (3.5), $x_n=P_{C_n}^{f}x$, which from (a) of Lemma 1.4 implies

$$〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(x_n),y-x_n〉\le 0,\mathrm{\forall }y\in C_n.$$

Since $F\subset C_n$, we have

$$〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(x_n),w-x_n〉\le 0,\mathrm{\forall }w\in F.$$

(3.10)

From (b) of Lemma 1.4 we have

$$\begin{array}{rcl}{D}_f(x_n,x)& =& D_f(P_{C_n}^{f}x,x)\le D_f(w,x)-D_f(w,P_{C_n}^{f}x)\\ \le & D_f(w,x),\mathrm{\forall }n\ge 1,w\in F.\end{array}$$

(3.11)

This implies that $\{D_f(x_n,x)\}$ is bounded, from Lemma 1.7, $\{x_n\}$ is bounded. By the construction of $C_n$, we have $x_m\in C_m\subset C_n$, and $x_n=P_{C_n}^{f}x$, for any positive integer $m\ge n$. Then we obtain

$$\begin{array}{rl}{D}_f(x_m,x_n)& =D_f(x_m,P_{C_n}^{f}x)\le D_f(x_m,x)-D_f(P_{C_n}^{f}x,x)\\ =D_f(x_m,x)-D_f(x_n,x).\end{array}$$

(3.12)

In particular,

$$D_f(x_{n+1},x_n)\le D_f(x_{n+1},x)-D_f(x_n,x).$$

Since $x_n=P_{C_n}^{f}x$ and $x_{n+1}=P_{C_{n+1}}^{f}x\in C_{n+1}\subset C_n$, we obtain $D_f(x_n,x)\le D_f(x_{n+1},x)$, $\mathrm{\forall }n\ge 1$. This shows that $\{D_f(x_n,x)\}$ is nondecreasing and hence the limit ${lim}_{n\to \mathrm{\infty }}{D}_f(x_n,x)$ exists. Thus from (3.12), taking the limit as $m,n\to \mathrm{\infty }$, we obtain ${lim}_{n\to \mathrm{\infty }}{D}_f(x_m,x_n)=0$. Since f is totally convex on bounded subsets of E, f is sequentially consistent (see [17]). It follows that $\parallel x_m-x_n\parallel \to 0$ as $m,n\to \mathrm{\infty }$. Hence $\{x_n\}$ is Cauchy sequence in C. As $\{x_n\}$ is Cauchy in a complete space E, there exists $p\in E$ such that $x_n\to p$ as $n\to \mathrm{\infty }$. Clearly $p\in C$.

Since $D_f(x_m,x_n)\to 0$, as $m,n\to \mathrm{\infty }$, we have in particular

$$\underset{n\to \mathrm{\infty }}{lim}{D}_f(x_{n+1},x_n)=0,$$

(3.13)

and this further implies that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =0.$$

(3.14)

Step V. Next we show that $x_n\to p\in F$.

Since $x_{n+1}=P_{C_{n+1}}^{f}x\in C_{n+1}$, we have from (3.5)

$$D_f(x_n,w_n)\le \frac{1}{1-k}〈\mathrm{\nabla }f(x_n)-\mathrm{\nabla }f(T_n{x}_n),x_n-x_{n+1}〉$$

(3.15)

$$+〈\mathrm{\nabla }f(T_n{x}_n)-\mathrm{\nabla }f(w_n),x_n-x_{n+1}〉,$$

(3.16)

which implies that ${lim}_{n\to \mathrm{\infty }}{D}_f(x_n,w_n)=0$. Since f is totally convex on bounded subsets of E, f is sequentially consistent (see [17]). It follows that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-w_n\parallel =0.$$

(3.17)

From (3.14) and (3.17), we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-w_n\parallel =0.$$

(3.18)

Since f is uniformly Fréchet differentiable, it follows from Lemma 1.1 that ∇f is uniformly continuous and f is uniformly continuous on bounded subsets of E (see [33], Theorem 1.8). Hence

$$\underset{n\to \mathrm{\infty }}{lim}\parallel \mathrm{\nabla }f(x_{n+1})-\mathrm{\nabla }f(w_n)\parallel =0$$

(3.19)

and

$$\underset{n\to \mathrm{\infty }}{lim}|f(x_{n+1})-f(w_n)|=0.$$

(3.20)

Since $x_{n+1}\in C_{n+1}$, it follows from (3.6), (3.7) that

$$\begin{array}{r}f(x_{n+1})-f(w_n)-〈\mathrm{\nabla }f(w_n),x_{n+1}-w_n〉\\ =D_f(x_{n+1},w_n)\le D_f(x_{n+1},y_n)\le D_f(x_{n+1},x_n)+\frac{k}{1-k}〈\mathrm{\nabla }f(x_n)-\mathrm{\nabla }f(T_n{x}_n),x_n-x_{n+1}〉,\end{array}$$

which implies from (3.20), (3.18), (3.13), and (3.14) that

$$\underset{n\to \mathrm{\infty }}{lim}{D}_f(x_{n+1},y_n)=0.$$

From the sequential consistency of f, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-y_n\parallel =0;$$

(3.21)

from (3.14) and (3.21), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-y_n\parallel =0,$$

(3.22)

which implies that $y_n\to p\in C$, since $x_n\to p\in C$. From the uniform continuity of ∇f, we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel \mathrm{\nabla }f(x_n)-\mathrm{\nabla }f(y_n)\parallel =0.$$

(3.23)

From (3.5), we have

$$\parallel \mathrm{\nabla }f(T_n{x}_n)-\mathrm{\nabla }f(x_n)\parallel =\frac{1}{1-{\alpha }_n}\parallel \mathrm{\nabla }f(x_n)-\mathrm{\nabla }f(y_n)\parallel ,$$

which implies from (3.23) that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel \mathrm{\nabla }f(T_n{x}_n)-\mathrm{\nabla }f(x_n)\parallel =0.$$

(3.24)

Since f is strongly coercive and uniformly convex on bounded subsets of E, $f^{\ast }$ is uniformly Fréchet differentiable on bounded sets. Moreover, $f^{\ast }$ is bounded on bounded sets, and from (3.24) we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel T_n{x}_n-x_n\parallel =0.$$

(3.25)

On the other hand, we see that

$$\begin{array}{rcl}\parallel x_n-T_{n+l}{x}_n\parallel & \le & \parallel x_n-x_{n+l}\parallel +\parallel x_{n+l}-T_{n+l}{x}_{n+l}\parallel \\ +\parallel T_{n+l}{x}_{n+l}-T_{n+l}{x}_n\parallel \\ \le & (1+L)\parallel x_n-x_{n+l}\parallel +\parallel x_{n+l}-T_{n+l}{x}_{n+l}\parallel \end{array}$$

for all $l\in \{1,2,\dots ,N\}$, where $L:={sup}_{1\le i\le N}{L}_i$. It follows from (3.14) and (3.25) that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-T_{n+l}{x}_n\parallel =0$$

for all $l\in \{1,2,\dots ,N\}$. Thus

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-T_l{x}_n\parallel =0$$

(3.26)

for all $l\in \{1,2,\dots ,N\}$. Since $x_n\to p$ as $n\to \mathrm{\infty }$, by the closedness of $T_l$ for each $l\in \{1,2,\dots ,N\}$, we obtain $p\in {\bigcap }_{l=1}^{N}F(T_l)$.

Also, since $y_n\to p$ as $n\to \mathrm{\infty }$, we have from Lemma 2.3, for each $j=1,2,\dots ,m$,

$$0\le D_f(p,u_{jn})=D_f(p,{Res}_{g_j}^f{y}_n)\le D_f(p,y_n)\to 0\text{as }n\to \mathrm{\infty }.$$

Then we have from Lemma 1.5 that ${lim}_{n\to \mathrm{\infty }}\parallel p-u_{jn}\parallel =0$, for each $j=1,2,\dots ,m$. Consequently, we have

$$\parallel u_{jn}-y_n\parallel \le \parallel u_{jn}-p\parallel +\parallel p-y_n\parallel \to 0\text{as }n\to \mathrm{\infty }.$$

(3.27)

From the uniform continuity of ∇f, for each $j=1,2,\dots ,m$ we have

$$\underset{n\to \mathrm{\infty }}{lim}\parallel \mathrm{\nabla }f(u_{jn})-\mathrm{\nabla }f(y_n)\parallel =0.$$

(3.28)

From (2.3), we have, for $j=1,2,\dots ,m$,

$$g_j(u_{jn},y)+〈\mathrm{\nabla }f(u_{jn})-\mathrm{\nabla }f(y_n),y-u_{jn}〉\ge 0,\mathrm{\forall }y\in C.$$

Furthermore, using (A2) in the last inequality, we obtain

$$〈\mathrm{\nabla }f(u_{jn})-\mathrm{\nabla }f(y_n),y-u_{jn}〉\ge g_j(y,u_{jn}),\mathrm{\forall }y\in C.$$

By (A4), (3.28), and $u_{jn}\to p$ as $n\to \mathrm{\infty }$, we have

$$g_j(y,p)\le 0,\mathrm{\forall }y\in C.$$

(3.29)

Let $z_t:=ty+(1-t)p$ for $t\in (0,1]$ and $y\in C$. This implies that $z_t\in C$. This yields $g_j(z_t,p)\le 0$. It follows from (A1) and (A4) that

$$\begin{array}{rcl}0& =& g_j(z_t,z_t)\le t{g}_j(z_t,y)+(1-t)g_j(z_t,p)\\ \le & t{g}_j(z_t,y),\end{array}$$

and hence

$$0\le g_j(z_t,y).$$

From condition (A3), we obtain

$$g_j(p,y)\ge 0,\mathrm{\forall }y\in C\text{ and }\mathrm{\forall }j\in \{1,2,3,\dots ,m\}.$$

This implies that $p\in EP(g_j)$, for each $j=1,2,\dots ,m$. Thus, $p\in {\bigcap }_{j=1}^{m}EP(g_j)$. Hence we have $p\in F=({\bigcap }_{i=1}^{N}F(T_i))\cap ({\bigcap }_{j=1}^{m}EP(g_j))$.

Step VI. Finally, we show that $p=P_F^{f}x$. Setting $n\to \mathrm{\infty }$ in (3.10), we obtain

$$〈\mathrm{\nabla }f(x)-\mathrm{\nabla }f(p),w-p〉\le 0,\mathrm{\forall }w\in F.$$

By (a) of Lemma 1.4, we have $p=P_F^{f}x$. □

Here we give an example of a quasi-Bregman strictly peudocontractive mapping which is not quasi-ϕ strictly pseudocontractive mapping; this shows that the former class is a generalization of the latter.

Example 3.3 Let $E=\mathbb{R}$, $C=[-1,0]$ and define $T,f:[-1,0]\to \mathbb{R}$ by $f(x)=x$ and $Tx=2x$, for all $x\in [-1,0]$. We want to show that T is a quasi-Bregman strictly pseudocontractive but not quasi-ϕ strictly pseudocontractive.

Proof From the definition it is clear that f is proper, lower semi-continuous, and convex, and also $F(T)=\{0\}$. By the definition of quasi-Bregman strict pseudocontractivity, we find $k\in [0,1)$ such that $D_f(p,Tx)\le D_f(p,x)+k{D}_f(x,Tx)$ for all $x\in C$ and $p\in F(T)$. Now,

$$\begin{array}{c}D(0,Tx)=f(0)-f(Tx)-〈\mathrm{\nabla }f(Tx),0-Tx〉\hfill \\ \phantom{D(0,Tx)}=0-2x-〈\mathrm{\nabla }f(2x),0-2x〉\hfill \\ \phantom{D(0,Tx)}=-2x-〈2,-2x〉\hfill \\ \phantom{D(0,Tx)}=-2x+4x=2x,\hfill \end{array}$$

(3.30)

$$\begin{array}{c}D(0,x)=f(0)-f(x)-〈\mathrm{\nabla }f(x),0-x〉\hfill \\ \phantom{D(0,x)}=0-x-〈1,-x〉\hfill \\ \phantom{D(0,x)}=-x+x=0\hfill \end{array}$$

(3.31)

and

$$\begin{array}{rcl}D(x,Tx)& =& f(x)-f(Tx)-〈\mathrm{\nabla }f(Tx),x-Tx〉\\ =& x-2x-〈2,x-2x〉\\ =& -x+2x=x.\end{array}$$

(3.32)

From (3.30), (3.31), and (3.32), we obtain

$$\begin{array}{rcl}D(0,Tx)& =& 2x\le x\\ \le & 0+kx,\mathrm{\forall }x\in [-1,0],k\in [0,1)\\ \le & D(0,x)+kD(x,Tx),\mathrm{\forall }x\in [-1,0],k\in [0,1).\end{array}$$

Therefore

$$D(0,Tx)\le D(0,x)+kD(x,Tx),\mathrm{\forall }x\in [-1,0],k\in [0,1).$$

Hence, T is a quasi-Bregman strictly pseudocontractive map.

Further,

$$\begin{array}{c}\varphi (0,Tx)={|0|}^2-2〈0,J(Tx)〉+{|Tx|}^2\hfill \\ \phantom{\varphi (0,Tx)}=0-2〈0,J(2x)〉+{|2x|}^2\hfill \\ \phantom{\varphi (0,Tx)}=4{|x|}^2,\hfill \end{array}$$

(3.33)

$$\begin{array}{c}\varphi (0,x)={|0|}^2-2〈0,J(x)〉+{|x|}^2\hfill \\ \phantom{\varphi (0,x)}=0-2〈0,J(x)〉+{|x|}^2\hfill \\ \phantom{\varphi (0,x)}={|x|}^2\hfill \end{array}$$

(3.34)

and

$$\begin{array}{rcl}\varphi (x,Tx)& =& {|x|}^2-2〈x,J(Tx)〉+{|Tx|}^2\\ =& {|x|}^2-2〈x,J(2x)〉+4{|x|}^2\\ =& {|x|}^2-4〈x,J(x)〉+4{|x|}^2\\ =& {|x|}^2-4{|x|}^2+4{|x|}^2\\ =& {|x|}^2.\end{array}$$

(3.35)

Since $4{|x|}^2>{|x|}^2+k{|x|}^2$, for all $k\in [0,1)$ and for all $x\in [-1,0]$,

$$\varphi (0,Tx)\le \varphi (0,x)+k\varphi (x,Tx),\mathrm{\forall }x\in [-1,0]$$

cannot hold for any $k\in [0,1)$. Hence, T is not a quasi-ϕ strictly pseudocontractive map. □

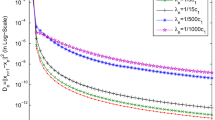
4 Numerical example

In this section we discuss the direct application of Theorem 3.2 on a typical example on a real line. Consider the following:

$$\begin{array}{c}\mathbb{E}=\mathbb{R},C=[-1,1],g(z,y)=y^2+yz-2z^2,\hfill \\ f(x)=\frac{2}{3}{x}^2,\mathrm{\nabla }f(x)=\frac{4}{3}x,Tx=-2x,\hfill \\ f^{\ast }\left(x^{\ast }\right)=sup\{〈x^{\ast },x〉-f(x):x\in \mathbb{E}\},\hfill \\ f^{\ast }(z)=\frac{3}{8}{z}^2,\mathrm{\nabla }{f}^{\ast }(z)=\frac{3}{4}z,{\alpha }_n=\frac{n+1}{4n},\hfill \\ {\alpha }_n\mathrm{\nabla }f(x_n)+(1-{\alpha }_n)\mathrm{\nabla }f(T{x}_n)=\frac{-(5n-3)}{3n}{x}_n,\hfill \\ k=1/2,x_1=1/2\in C,\hfill \end{array}$$

then the scheme can be simplified as

$$\begin{array}{r}{y}_n=\mathrm{\nabla }{f}^{\ast }({\alpha }_n\mathrm{\nabla }f(x_n)+(1-{\alpha }_n)\mathrm{\nabla }f(T{x}_n)),\\ \therefore y_n=\frac{-(5n-3)}{4n}{x}_n,\\ u_n={Res}_g^f{y}_n=\frac{4}{13}{y}_n,\\ w_n=\mathrm{\nabla }{f}^{\ast }(\mathrm{\nabla }f(u_n))=u_n,\\ C_{n+1}=\{w\in C_n:w\le x_n-\frac{(1-k){(x_n-w_n)}^2}{2[(1+2k)x_n-(1-k)w_n]}\},\\ x_{n+1}=P_{C_{n+1}}^f(x_1)=x_n-\frac{(1-k){(x_n-w_n)}^2}{2[(1+2k)x_n-(1-k)w_n]}.\end{array}$$