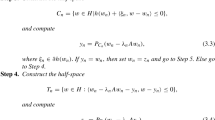Abstract
In this paper, we introduce an iterative scheme for finding a common element of the sets of fixed points for multivalued nonexpansive mappings, strict pseudo-contractive mappings and the set of solutions of an equilibrium problem for a pseudomonotone, Lipschitz-type continuous bifunctions. We prove the strong convergence of the sequence, generated by the proposed scheme, to the solution of the variational inequality. Our results generalize and improve some known results.
MSC:47H10, 65K10, 65K15, 90C25.
Similar content being viewed by others
1 Introduction
In 1967, Browder and Petryshyn [1] introduced a concept of strict pseudo-contractive in a real Hilbert space. Let C be a nonempty subset of a real Hilbert space H, and let be a single-valued mapping. A mapping T is called a β-strict pseudo-contractive on C [1] if there exists a constant such that
We use to denote the set of all fixed points of T; . Note that the class of strictly pseudo-contractive mappings strictly includes the class of nonexpansive mappings, which are the mappings T on C such that
for all (see [2]). Strictly pseudocontractive mappings have more powerful applications than nonexpansive mappings in solving inverse problems, see Scherzer [3]. In the literature, many interesting and important results have been appeared to approximate the fixed points of pseudo-contractive mappings. For example, see [4–6] and the references therein.
A subset is called proximal if for each , there exists an element such that
We denote by , and the collection of all nonempty closed bounded subsets, nonempty compact subsets, and nonempty proximal bounded subsets of C, respectively. The Hausdorff metric H on is defined by
for all .
Let be a multivalued mapping. An element is said to be a fixed point of T if . A multivalued mapping is called nonexpansive if
Much work has been done on the existence of common fixed points for a pair consisting of a single-valued and a multivalued mapping, see, for instance [7–14]. Let f be a bifunction from into ℝ, such that for all . Consider the classical Ky Fan inequality. Find a point such that
where is convex and subdifferentiable on C for every . The set of solutions for this problem is denoted by . In fact, the Ky Fan inequality can be formulated as an equilibrium problem. Further, if for every , where F is a mapping from C into H, then the Ky Fan inequality problem (equilibrium problem) becomes the classical variational inequality problem, which is formulated as finding a point such that
Such problems arise frequently in mathematics, physics, engineering, game theory, transportation, economics and network. Due to importance of the solutions of such problems, many researchers are working in this area and studying on the existence of the solutions of such problems, see, e.g., [15–20]. Further, in the recent years, iterative algorithms for finding a common element of the set of solutions of equilibrium problem and the set of fixed points of nonexpansive mappings in a real Hilbert space have been studied by many authors (see, e.g., [21–33]).
Definition 1.1 Let C be a nonempty closed convex subset of a Hilbert space H. The bifunction is said to be
-
(i)
strongly monotone on C with if
-
(ii)
monotone on C if
-
(iii)
pseudomonotone on C if
-
(iv)
Lipschitz-type continuous on C with constants and (in the sense of Mastroeni [34]) if
Recently, Anh [35, 36] introduced some methods for finding a common element of the set of solutions of monotone Lipschitz-type continuous equilibrium problem and the set of fixed points of a nonexpansive mapping T in a Hilbert space H. In [35], he proved the following theorem.
Theorem 1.2 Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let be a monotone, continuous, and Lipschitz-type continuous bifunction, and let be convex and subdifferentiable on C for every . Let h be a contraction of C into itself with constant , let S be a nonexpansive mapping of C into itself, and let . Let , and be sequences generated by and by
where , and , , , and satisfy the following conditions:
-
(i)
, ,
-
(ii)
, , where ,
-
(iii)
and ,
-
(iv)
.
Then, the sequences , and converge strongly to which solves the variational inequality
In this paper, we introduce an iterative algorithm for finding a common element of the sets of fixed points for multivalued nonexpansive mappings, strict pseudo-contractive mappings and the set of solutions of an equilibrium problem for a pseudomonotone, Lipschitz-type continuous bifunctions. We prove the strong convergence of the sequence generated by the proposed algorithm to the solution of the variational inequality. Our results generalize and improve a number of known results including the results of Anh [35].
2 Preliminaries
Let H be a real Hilbert space with inner product and the norm . Let be a sequence in H, and let . Weak convergence of to x is denoted by , and strong convergence by . Let C be a nonempty closed convex subset of H. The nearest point projection from H to C, denoted by , assigns to each the unique point with the property
It is known that is a nonexpansive mapping, and for each ,
Definition 2.1 Let C be a nonempty, closed and convex subset of a Hilbert space H. Denote by the normal cone of C at , i.e.,
Definition 2.2 Let C be a nonempty, closed and convex subset of a Hilbert space H, and let be a bifunction. For each , by we denote the subgradient of the function at u, i.e.,
The following lemmas are crucial for the proofs of our results.
Lemma 2.3 In a Hilbert space H, the following inequality holds:
Lemma 2.4 [37]
Let be a sequence of nonnegative real numbers, let be a sequence in with , let be a sequence of nonnegative real numbers with , and let be a sequence of real numbers with . Suppose that the following inequality holds:
Then .
Lemma 2.5 [38]
Let H be a real Hilbert space. Then for all and with , we have
Lemma 2.6 [39]
Let be a sequence of real numbers such that there exists a subsequence of such that for all . Then there exists a nondecreasing sequence such that , and the following properties are satisfied by all (sufficiently large) numbers :
In fact,
Lemma 2.7 [36]
Let C be a nonempty closed convex subset of a real Hilbert space H, and let be a pseudomonotone and Lipschitz-type continuous bifunction. For each , let be convex and subdifferentiable on C. Let , and be the sequences, generated by and by
Then for each ,
Lemma 2.8 [5]
Let C be nonempty closed convex subset of a real Hilbert space H, and let be β-pseudo-contraction mapping. Then is demiclosed at 0. That is, if is a sequence in C such that and , then .
Lemma 2.9 [5]
Let C be a closed convex subset of a Hilbert space H, and let be a β-strict pseudo-contraction on C and the fixed-point set of T is nonempty, then is closed and convex.
Lemma 2.10 [40]
Let C be a closed convex subset of a real Hilbert space H. Let be a nonexpansive multivalued mapping. Assume that for all . Then is closed and convex.
Lemma 2.11 [25]
Let C be a nonempty closed convex subset of a real Hilbert space H. Let be a nonexpansive multivalued mapping. If and , then .
3 Main results
Now, we are in a position to give our main results.
Theorem 3.1 Let C be a nonempty closed convex subset of a real Hilbert space H, and let be a monotone, continuous, and Lipschitz-type continuous bifunction. Suppose that is convex and subdifferentiable on C for all . Let, be a multivalued nonexpansive mapping, and let be a β-strict pseudo-contraction mapping. Assume that and for each . Let h be a k-contraction of C into itself. Let , and be sequences generated by and by
where . Let , , , and satisfy the following conditions:
-
(i)
, , ,
-
(ii)
, where ,
-
(iii)
, and .
Then, the sequence converges strongly to , which solves the variational inequality
Proof Let . It easy to see that Qh is a contraction. By the Banach contraction principle, there exists a such that . Applying Lemma 2.7, we have
This implies that
Since T is nonexpansive and , by (4) we have
We show that is bounded. Indeed, using inequality (4), (5) and Lemma 2.5, we have
It follows that
Since , we get that . This implies that
By induction, we get
for all . This implies that is bounded, and we also obtain that , , and are bounded. Next, we show that
Indeed, using inequality (6), we have
Therefore, we have
In order to prove that as , we consider the following two cases.
Case 1. Suppose that there exists such that is nonincreasing, for all . Boundedness of implies that is convergent. Since is bounded and , from (7) and our assumption that , we obtain that
By similar argument we can obtain that
From this with inequality , it follows that
Next, we show that
where . To show this inequality, we choose a subsequence of such that
Since is bounded, there exists a subsequence of , which converges weakly to . Without loss of generality, we can assume that . From inequality (9), we have . Now, since , from Lemma 2.8, we have . Also from (8), we have
It follows from Lemma 2.9 that . Now, we show that . Since is convex on C for each , we see that
if and only if
where is the (outward) normal cone of C at . This follows that
where and . By the definition of the normal cone , we have
Since is subdifferentiable on C, there exists such that
(see, [41, 42]). Combining this with (10), we have
Hence
From (8), we have that . Now by continuity of f and assumption that , we have
This implies that , and hence . Since and , it follows that
By using Lemma 2.3 and inequality (6), we have
This implies that
From Lemma 2.4, we conclude that the sequence converges strongly to q.
Case 2. Assume that there exists a subsequence of such that
for all . In this case from Lemma 2.6, there exists a nondecreasing sequence of ℕ for all (for some large enough) such that as , and the following inequalities hold for all ,
From (3), we obtain , and similarly we obtain
Following an argument similar to that in Case 1, we have
Thus, by Lemma 2.6, we have
Therefore, converges strongly to . This completes the proof. □
Now, let be a multivalued mapping, and let
Then, we have . Indeed, if , then , hence . On the other hand, if , since , we have . Now, using the similar arguments as in the proof of Theorem 3.1, we obtain the following result by replacing T by , and removing the strict condition for all .
Theorem 3.2 Let C be a nonempty closed convex subset of a real Hilbert space H, and let be a monotone, continuous, and Lipschitz-type continuous bifunction. Suppose that is convex and subdifferentiable on C for all . Let be a multivalued mapping such that is nonexpansive, and let be a β-strict pseudo-contraction mapping. Assume that . Let h be a k-contraction of C into itself. Let , and be sequences generated by and by
where . Let , , , and satisfy the following conditions:
-
(i)
, , ,
-
(ii)
, where ,
-
(iii)
, and .
Then, the sequence converges strongly to , which solves the variational inequality
As a consequence, we obtain the following result for single-valued mappings.
Corollary 3.3 Let C be a nonempty closed convex subset of a real Hilbert space H, and let be a monotone, continuous, and Lipschitz-type continuous bifunction. Suppose that is convex and subdifferentiable on C for all . Let be a nonexpansive mapping, and let be a β-strict pseudo-contraction mapping. Assume that . Let h be a k-contraction of C into itself. Let , and be sequences generated by and by
Let , , , and satisfy the following conditions:
-
(i)
, , ,
-
(ii)
, where ,
-
(iii)
, and .
Then, the sequence converges strongly to , which solves the variational inequality
4 Application to variational inequalities
In this section, we consider the particular Ky Fan inequality, corresponding to the function f, defined by for every with . Then, we obtain the classical variational inequality
The set of solutions of this problem is denoted by . In that particular case, the solution of the minimization problem
can be expressed as
Let F be L-Lipschitz continuous on C. Then
Therefore,
and, hence, f satisfies Lipschitz-type continuous condition with . Now, using Theorem 3.1, we obtain the following convergence theorem for finding a common element of the set of common fixed points of a strict pseudo-contractive mapping and a multivalued nonexpansive mapping and the solution set of the variational inequality problem.
Theorem 4.1 Let C be a nonempty closed convex subset of a real Hilbert space H, and let F be a function from C to H such that F is monotone and L-Lipschitz continuous on C. Let, be a multivalued nonexpansive mapping, and let be a β-strict pseudo-contraction mapping. Assume that and for each . Let h be a k-contraction of C into itself. Let , , and let be sequences generated by and by
where . Let , , , and satisfy the following conditions:
-
(i)
, , ,
-
(ii)
,
-
(iii)
, and .
Then, the sequence converges strongly to , which solves the variational inequality
References
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert spaces. J. Math. Anal. Appl. 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Chidume CE, Mutangadura SA: An example on the Mann iteration method for Lipschitz pseudo-contractions. Proc. Am. Math. Soc. 2001, 129: 2359–2363. 10.1090/S0002-9939-01-06009-9
Scherzer O: Convergence criteria of iterative methods based on Landweber iteration for solving nonlinear problems. J. Math. Anal. Appl. 1991, 194: 911–933.
Acedo GL, Xu HK: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Anal. 2007, 67: 2258–2271. 10.1016/j.na.2006.08.036
Marino G, Xu HK: Weak and strong convergence theorems for strictly pseudo-contractions in Hilbert spaces. J. Math. Anal. Appl. 2007, 329: 336–349. 10.1016/j.jmaa.2006.06.055
Zhou HY: Convergence theorems of common fixed points for a finite family of Lipschitz pseudo-contractions in Banach spaces. Nonlinear Anal. 2008, 68: 2977–2983. 10.1016/j.na.2007.02.041
Dhompongsa S, Kaewkhao A, Panyanak B:Lim’s theorem for multivalued mappings in spaces. J. Math. Anal. Appl. 2005, 312: 478–487. 10.1016/j.jmaa.2005.03.055
Latif A, Tweddle I: Some results on coincidence points. Bull. Aust. Math. Soc. 1999, 59: 111–117. 10.1017/S0004972700032652
Hussain N, Khamsi MA: On asymptotic pointwise contractions in metric spaces. Nonlinear Anal. 2009, 71: 4423–4429. 10.1016/j.na.2009.02.126
Abkar A, Eslamian M:Common fixed point results in spaces. Nonlinear Anal. 2011, 74: 1835–1840. 10.1016/j.na.2010.10.056
Espinola R, Nicolae A: Geodesic Ptolemy spaces and fixed points. Nonlinear Anal. 2011, 74: 27–34. 10.1016/j.na.2010.08.009
Garcia-Falset J, Llorens-Fuster E, Moreno-Galvez E: Fixed point theory for multivalued generalized nonexpansive mappings. Appl. Anal. Discrete Math. 2012, 6: 265–286. 10.2298/AADM120712017G
Markin JT: Fixed points for generalized nonexpansive mappings in R-trees. Comput. Math. Appl. 2011, 62: 4614–4618. 10.1016/j.camwa.2011.10.045
Abkar A, Eslamian M: Fixed point theorems for Suzuki generalized nonexpansive multivalued mappings in Banach spaces. Fixed Point Theory Appl. 2010., 2010: Article ID 457935 10.1155/2010/457935
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63: 123–145.
Flam SD, Antipin AS: Equilibrium programming using proximal-link algorithms. Math. Program. 1997, 78: 29–41.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 2005, 6: 117–136.
Iiduka H, Yamada I: A use of conjugate gradient direction for the convex optimization problem over the fixed point set of a nonexpansive mapping. SIAM J. Optim. 2009, 19: 1881–1893. 10.1137/070702497
Iiduka H, Yamada I: A subgradient-type method for the equilibrium problem over the fixed point set and its applications. Optimization 2009, 58: 251–261. 10.1080/02331930701762829
Mainge PE: A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J. Control Optim. 2008, 47: 1499–1515. 10.1137/060675319
Tada A, Takahashi W: Weak and strong convergence theorems for a nonexpansive mapping and an equilibrium problem. J. Optim. Theory Appl. 2007, 133: 359–370. 10.1007/s10957-007-9187-z
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J. Math. Anal. Appl. 2007, 331: 506–515. 10.1016/j.jmaa.2006.08.036
Ansari QH, Khan Z: Densely relative pseudomonotone variational inequalities over product of sets. J. Nonlinear Convex Anal. 2006, 7(2):179–188.
Ceng LC, Ansari QH, Yao JC: Viscosity approximation methods for generalized equilibrium problems and fixed point problems. J. Glob. Optim. 2009, 43: 487–502. 10.1007/s10898-008-9342-6
Eslamian M: Convergence theorems for nonspreading mappings and nonexpansive multivalued mappings and equilibrium problems. Optim. Lett. 2011. 10.1007/s11590-011-0438-4
Ceng LC, Yao JC: Hybrid viscosity approximation schemes for equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Appl. Math. Comput. 2008, 198: 729–741. 10.1016/j.amc.2007.09.011
Ceng LC, Yao JC: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. J. Comput. Appl. Math. 2008, 214: 186–201. 10.1016/j.cam.2007.02.022
Ceng LC, Schaible S, Yao JC: Implicit iteration scheme with perturbed mapping for equilibrium problems and fixed point problems of finitely many nonexpansive mappings. J. Optim. Theory Appl. 2008, 139: 403–418. 10.1007/s10957-008-9361-y
Ceng LC, Al-Homidan S, Ansari QH, Yao JC: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. J. Comput. Appl. Math. 2009, 223: 967–974. 10.1016/j.cam.2008.03.032
Ceng LC, Guu SM, Yao JC: Hybrid iterative method for finding common solutions of generalized mixed equilibrium and fixed point problems. Fixed Point Theory Appl. 2012., 2012: Article ID 92
Ceng LC, Ansari QH, Schaible S: Hybrid extragradient-like methods for generalized mixed equilibrium problems, systems of generalized equilibrium problems and optimization problems. J. Glob. Optim. 2012, 53: 69–96. 10.1007/s10898-011-9703-4
Ceng LC, Yao JC: A relaxed extragradient-like method for a generalized mixed equilibrium problem, a general system of generalized equilibria and a fixed point problem. Nonlinear Anal. 2010, 72: 1922–1937. 10.1016/j.na.2009.09.033
Ceng LC, Petrusel A, Yao JC: Iterative approaches to solving equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. J. Optim. Theory Appl. 2009, 143: 37–58. 10.1007/s10957-009-9549-9
Mastroeni G: On auxiliary principle for equilibrium problems. In Equilibrium Problems and Variational Models. Edited by: Daniele P, Giannessi F, Maugeri A. Kluwer Academic, Dordrecht; 2003.
Anh PN: A hybrid extragradient method extended to fixed point problems and equilibrium problems. Optimization 2013, 62: 271–283. 10.1080/02331934.2011.607497
Anh PN: Strong convergence theorems for nonexpansive mappings and Ky Fan inequalities. J. Optim. Theory Appl. 2012. 10.1007/s10957-012-0005-x
Xu HK: An iterative approach to quadratic optimization. J. Optim. Theory Appl. 2003, 116: 659–678. 10.1023/A:1023073621589
Osilike MO, Igbokwe DI: Weak and strong convergence theorems for fixed points of pseudocontractions and solutions of monotone type operator equations. Comput. Math. Appl. 2000, 40: 559–567. 10.1016/S0898-1221(00)00179-6
Mainge PE: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set-Valued Anal. 2008, 16: 899–912. 10.1007/s11228-008-0102-z
Dhompongsa S, Kaewkhao A, Panyanak B:On Kirk strong convergence theorem for multivalued nonexpansive mappings on spaces. Nonlinear Anal. 2012, 75: 459–468. 10.1016/j.na.2011.08.046
Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 1976, 14: 877–898. 10.1137/0314056
Daniele P, Giannessi F, Maugeri A: Equilibrium Problems and Variational Models. Kluwer, Norwell; 2003.
Acknowledgements
This article was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. Therefore, the second author acknowledges with thanks DSR, KAU for financial support. The authors thank the referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vahidi, J., Latif, A. & Eslamian, M. New iterative scheme with strict pseudo-contractions and multivalued nonexpansive mappings for fixed point problems and variational inequality problems. Fixed Point Theory Appl 2013, 213 (2013). https://doi.org/10.1186/1687-1812-2013-213
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-213