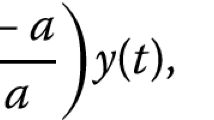Meir-Keeler ɑ-contractive fixed and common fixed point theorems

Abstract

Generalized Meir-Keeler α-contractive functions and pairs are introduced and their fixed and common fixed point theorems are obtained. Also, the so-called generalized Meir-Keeler α-f-contractive maps commuting with f are introduced and their coincidence and common fixed point theorems are investigated. New sufficient conditions different from those in (Samet et al. in Nonlinear Anal. 75:2154-2165, 2012) are used. An application to the coupled fixed point is established as well. An example is given to show that the α-Meir-Keeler generalization is real.

AMS Subject Classification: 47H10, 54H25.

1 Introduction

Fixed point theory is of wide and endless applications in many fields of engineering and science. Its core, the Banach contraction principle, has attracted many researchers who tried to generalize it in different aspects. Some dealt with the contractive condition itself, of worth mentioning Meir-Keeler contractive type [1–4], some extended it to more generalized metric-type spaces [5–11] and others applied to common [12], coupled and tripled versions (see [13, 14] and the references therein). In 1969 Meir and Keeler [15] established a fixed point theorem in a metric space $(X,d)$ for mappings satisfying the following condition, called the Meir-Keeler type contractive condition:

$$\mathrm{\forall }ϵ>0,\mathrm{\exists }\delta >0\text{: }ϵ\le d(x,y)<\delta +ϵ\text{implies}d(fx,fy)<ϵ.$$

(1)

In 1978 Maiti and Pal [16] generalized a fixed point for maps satisfying the following condition:

$$\mathrm{\forall }ϵ>0,\mathrm{\exists }\delta >0\text{: }ϵ\le max\{d(x,y),d(x,fx),d(y,fy)\}<\delta +ϵ\text{implies}d(fx,fy)<ϵ.$$

(2)

Later in 1981, Park and Rhoades in [3] established fixed point theorems for a pair of mappings f, g satisfying a contractive condition that can be reduced to the following generalization of (2) when $f=g$.

(3)

In this article we develop the fixed point theorems for α-contractive type maps introduced recently in [17] (for the α-ψ-contractive multivalued case, see [18]) to Meir-Keeler versions and hence generalize the results obtained in [3] and the references therein. Then, we apply part of our results to the coupled case on the basis of Amini-Harandi [19].

2 Fixed and common fixed point theorems for generalized Meir-Keeler α-contractive maps and pairs

The first part of the following definition was introduced in [17].

Definition 1 Let $f,g:X\to X$ be self-mappings of a set X and $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping, then the mapping f is called α-admissible if

$$x,y\in X,\alpha (x,y)\ge 1\Rightarrow \alpha (fx,fy)\ge 1$$

and the pair $(f,g)$ is called α-admissible if

$$x,y\in X,\alpha (x,y)\ge 1\Rightarrow \alpha (fx,gy)\ge 1\text{and}\alpha (gx,fy)\ge 1.$$

Example 2 Let $X=\mathbb{R}$ and

$$\alpha (x,y)=\{\begin{array}{cc}1,\hfill & x,y\in [0,1],\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

Then the pair $(x^{1/2},x^{1/3})$ is α-admissible but the pair $(x^{1/2},x+1)$ is not α-admissible.

Definition 3 Let $(X,d)$ be a metric space and $f:X\to X$ be a self-mapping, $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping. Then f is called Meir-Keeler α-contractive if, given an $ϵ>0$, there exists a $\delta >0$ such that

$$ϵ\le d(x,y)<ϵ+\delta \text{implies}\alpha (x,y)d(fx,fy)<ϵ.$$

Definition 4 Let $(X,d)$ be a metric space and $f:X\to X$ be a self-mapping, $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping. Then f is called generalized Meir-Keeler α-contractive if, given an $ϵ>0$, there exists a $\delta >0$ such that

$$ϵ\le M_f(x,y)<ϵ+\delta \text{implies}\alpha (x,y)d(fx,fy)<ϵ,$$

where

$$M_f(x,y)=max\{d(x,y),d(x,fx),d(y,fy),\frac{d(x,fy)+d(y,fx)}{2}\}.$$

Definition 5 Let $(X,d)$ be a metric space and $f,g:X\to X$ be self-mappings, $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping. Then the pair $(f,g)$ is called generalized Meir-Keeler α-contractive if, given an $ϵ>0$, there exists a $\delta >0$ such that

$$ϵ\le M_{(f,g)}(x,y)<ϵ+\delta \text{implies}\alpha (x,y)d(fx,gy)<ϵ,$$

(4)

where

$$M_{(f,g)}(x,y)=max\{d(x,y),d(x,fx),d(y,gy),\frac{d(x,gy)+d(y,fx)}{2}\}.$$

We write $M_f(x,y)=M_{(f,f)}(x,y)$.

Clearly, f is generalized Meir-Keeler α-contractive if and only if $(f,f)$ is generalized Meir-Keeler α-contractive.

Definition 6 Let X be any set, $x_0\in X$ and f, g be self-maps of X. Define $x_{2n+1}=f{x}_{2n}$ and $x_{2n+2}=g{x}_{2n}$, $n=0,1,2,\dots$ . Then $\{x_n\}$ is called the $(f,g)$-orbit of $x_0$. If d is a metric on X, then $(X,d)$ is called $(f,g)$-orbitally complete if every Cauchy sequence in the $(f,g)$-orbit of $x_0$ is convergent and the map f or g is called orbitally continuous if it is continuous on the orbit.

The proof of the following lemma is immediate.

Lemma 7 Let $f,g:X\to X$ be self-mappings of a set X, $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping and $\{x_n\}$ be the $(f,g)$-orbit of $x_0$ with $\alpha (x_0,f{x}_0)\ge 1$. If the pair $(f,g)$ is α-admissible, then $\alpha (x_n,x_{n+1})\ge 1$ for all $n=0,1,2,\dots$ .

Theorem 8 Let $(X,d)$ be an $(f,g)$-orbitally complete metric space, where f, g are self-mappings of X. Also, let $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping. Assume the following:

• 1. $(f,g)$ is α-admissible and there exists an $x_0\in X$ such that $\alpha (x_0,f{x}_0)\ge 1$;

• 2. the pair $(f,g)$ is generalized Meir-Keeler α-contractive.

  Then the sequence $d_n=d(x_n,x_{n+1})$ is monotone decreasing. If, moreover, we assume that

• 3. on the $(f,g)$-orbit of $x_0$, we have $\alpha (x_n,x_j)\ge 1$ for all n even and $j>n$ odd and that f and g are continuous on the $(f,g)$-orbit of $x_0$.

Then either (1) f or g has a fixed point in the $(f,g)$-orbit $\{x_n\}$ of $x_0$ or (2) f and g have a common fixed point p and $lim{x}_n=p$. If, moreover, we assume that the following condition (H) holds: If $\{x_n\}$ is a sequence in X such that $\alpha (x_n,x_{n+1})\ge 1$ for all n and $x_n\to x$ implies $\alpha (x_n,x)\ge 1$ for all n, then uniqueness of the fixed point is obtained.

Proof Define $d_n=d(x_n,x_{n+1})$ for $n=0,1,2,\dots$ . If $d_n=0$ for some even integer n, then f has a fixed point. If $d_n=0$ for some odd integer n, then g has a fixed point. Hence, we may assume that $d_n\ne 0$ for each n. The fact that the pair $(f,g)$ is generalized Meir-Keeler α-contractive implies that

$$\alpha (x,y)d(fx,gy)<M_f(x,y)\text{for each }x,y\in X,x,y\ne 0.$$

(5)

Note that assumption (3) implies that $\alpha (x_0,f{x}_0)\ge 1$. Hence, since $(f,g)$ is α-admissible, then Lemma 7 implies that $\alpha (x_n,x_{n+1})\ge 1$ for all $n=0,1,2,\dots$ and hence by (5), we have

$$\begin{array}{rcl}{d}_{2n}& =& d(f{x}_{2n},g{x}_{2n-1})\\ \le & \alpha (x_{2n},x_{2n-1})d(f{x}_{2n},g{x}_{2n-1})\\ <& max\{d_{2n-1},\frac{d(x_{2n-1},x_{2n+1})}{2}\}\\ \le & max\{d_{2n-1},\frac{d_{2n-1}+d_{2n}}{2}\},\end{array}$$

(6)

whence $d_{2n}<d_{2n-1}$. □

Similarly, it can be shown that $d_{2n+1}<d_{2n}$. Thus, $\{d_n\}$ is monotone decreasing in n and converges to a limit, say ϱ.

Suppose $\varrho >0$. Then, for each $\delta >0$, there exists a positive integer $N=N(\delta )$ such that $\varrho \le d_N=d(x_N,x_{N+1})<\varrho +\delta$, where N can be chosen even. Thus, from assumption (1) and Lemma 7, we have $d_{N+1}\le \alpha (x_N,x_{N+1})d(f{x}_N,g{x}_{N+1})<\varrho$, a contradiction. Therefore, $\varrho =0$. To show that $\{x_n\}$ is Cauchy, we assume the contrary. Thus, there exists an ${ϵ}^{\mathrm{\prime }}>0$ such that for each integer N, there exist integers $m>n>N$ such that $d(x_m,x_n)\ge {ϵ}^{\mathrm{\prime }}$. Define ϵ by ${ϵ}^{\mathrm{\prime }}=2ϵ$. Choose a number δ, $0<\delta <ϵ$, for which (4) is satisfied. Since $\varrho =0$, there exists an integer $N=N(\delta )$ such that $d_i<\frac{\delta }{6}$ for $i\ge N$. With this choice of N, pick integers $m>n>N$ such that

$$d(x_m,x_n)\ge 2ϵ>\delta +ϵ,$$

(7)

in which it is clear that $m-n>6$. Otherwise, $d(x_m,x_n)\le {\sum }_{i=0}^5{d}_{i+n}<\delta <\delta +ϵ$, contradicting (7). Without loss of generality, we may assume that n is even since from (7) it follows that $d(x_m,x_{n+1})>ϵ+\frac{\delta }{3}$. From (7) there exists the smallest odd integer $j>n$ such that

$$d(x_n,x_j)\ge ϵ+\frac{\delta }{3}.$$

(8)

Hence, $d(x_n,x_{j-2})<ϵ+\frac{\delta }{3}$, and so $d(x_n,x_j)\le d(x_n,x_{j-2})+d_{j-1}+d_j<ϵ+\frac{\delta }{3}+2(\frac{\delta }{6})=ϵ+\frac{2\delta }{3}$. Therefore, we have

$$\begin{array}{rcl}ϵ& <& d(x_n,x_j)\le M_{(f,g)}(x_n,x_j)\\ \le & max\{d(x_n,x_j),\frac{d(x_n,x_{j+1})+d(x_j,x_{n+1})}{2}\}\\ \le & \frac{d(x_n,x_j)+d_j+d(x_j,x_n)+d_n}{2}\\ \le & d(x_n,x_j)+\frac{\delta }{6}\le ϵ+\delta ,\end{array}$$

so that, by (7) and assumption (3), $d(x_{n+1},x_{j+1})\le \alpha (x_n,x_j)d(x_{n+1},x_{j+1})<ϵ$. Then we have

$$\begin{array}{rcl}d(x_n,x_j)& \le & d_n+d(x_{n+1},x_{j+1})+d_j\\ <& \frac{\delta }{6}+ϵ+\frac{\delta }{6}=ϵ+\frac{\delta }{3}.\end{array}$$

This contradicts the choice of j in (8). Therefore, $\{x_n\}$ is Cauchy.

Since X is $(f,g)$-orbitally complete, $\{x_n\}$ converges to some point $p\in X$. Since f and g are orbitally continuous, then p is a common fixed point of f and g. To prove uniqueness, assume p is the common fixed point obtained as $x_n\to p$ and q is another common fixed point. Then (5) and the condition (H) yield

$$\begin{array}{rcl}d(p,q)& =& d(fp,q)\le d(fp,g{x}_n)+d(g{x}_n,q)\\ \le & \alpha (x_n,p)d(fp,g{x}_n)+d(g{x}_n,q)\\ <& M_{(f,g)}(x_n,p)+d(g{x}_n,q).\end{array}$$

If we let $n\to \mathrm{\infty }$, then we reach $d(p,q)<d(p,q)$, which implies that $p=q$.

Corollary 9 Let $(X,d)$ be an f-orbitally complete metric space, where f is a self-mapping of X. Also, let $\alpha :X\times X\to [0,\mathrm{\infty })$ be a mapping. Assume the following:

• 1. f is α-admissible and there exists an $x_0\in X$ such that $\alpha (x_0,f{x}_0)\ge 1$;

• 2. f is generalized Meir-Keeler α-contractive.

  Then the sequence $d_n=d(x_n,x_{n+1})$ is monotone decreasing. If, moreover, we assume that

• 3. on the f-orbit of $x_0$, we have $\alpha (x_n,x_j)\ge 1$ for all n even and $j>n$ odd.

Then either (1) f has a fixed point in the f-orbit $\{x_n\}$ of $x_0$ or (2) f has a fixed point p and $lim{x}_n=p$. If, moreover, we assume that the following condition (H) holds: If $\{x_n\}$ is a sequence in X such that $\alpha (x_n,x_{n+1})\ge 1$ for all n and $x_n\to x$, then $\alpha (x_n,x)\ge 1$ for all n, then uniqueness of the fixed point is obtained.

Since generalized Meir-Keeler α-contractions are Meir-Keeler α-contractions, then Corollary 9 is valid also for Meir-Keeler α-contractions. In the following example, the existence and uniqueness of the fixed point cannot be proved in the category of Meir-Keeler contractions, but can be proved by means of Corollary 9.

Example 10 Let $X=[0,2]$ with the absolute value metric $d(x,y)=|x-y|$. Define $f:X\to X$ by

$$f(x)=\{\begin{array}{cc}0,\hfill & x=\frac{1}{4},\hfill \\ 1,\hfill & x\in [0,\frac{1}{2})-\{\frac{1}{4}\},\hfill \\ \frac{3}{2},\hfill & x\in [\frac{1}{2},2].\hfill \end{array}$$

Then, for $ϵ=\frac{1}{2}$, $x=\frac{1}{4}$ and any $\delta >0$, we have $\frac{1}{2}\le |\frac{1}{4}-y|<\delta +\frac{1}{2}$ implies $y\in [\frac{1}{2},2]$ and hence $d(fx,fy)=d(0,\frac{3}{2})=\frac{3}{2}>ϵ$. Hence, f is not a Meir-Keeler contraction. However, f is a Meir-Keeler α-contraction, where

$$\alpha (x,y)=\{\begin{array}{cc}1,\hfill & x,y\in [\frac{1}{2},2],\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

Indeed, for $0<ϵ<1$ (the case $ϵ\ge 1$ is trivial, since $|fx-fy|\le 1$), let $\delta =(1-ϵ)$, then $ϵ\le \alpha (x,y)d(x,y)<\delta +ϵ=1$ implies that $x,y\in [\frac{1}{2},2]$ and hence $d(fx,fy)=|\frac{3}{2}-\frac{3}{2}|=0<ϵ$. Also, notice that f is continuous on the orbit of $x_0=1$ and that $\alpha (x_n,x_j)\ge 1$ for all n, j. Clearly, $p=\frac{3}{2}$ is the unique fixed point.

Remark 11 Note that the admissibility condition (1) in Theorem 8 is not enough to proceed to guarantee the existence of the fixed point. However, such an admissibility condition was used in obtaining the main result in Theorem 2.2 of [17].

3 Generalized Meir-Keeler α-f-contractive fixed points

Definition 12 Let f be a continuous self-map of a metric space $(X,d)$, $C_f=\{g:g:X\to X,\text{ such that }fg=gf\text{ and }gX\subseteq fX\}$, the sequence $\{f{x}_n\}$ defined by $f{x}_{n+1}=g{x}_n$, $n=0,1,2,\dots$ , with the understanding that if $f{x}_n=f{x}_{n+1}$ for some n, then $f{x}_{n+j}=f{x}_n$ for each $j\ge 0$ is called the f-iteration of $x_0$ under g.

Definition 13 Let f be a self-map of a metric space $(X,d)$ and $g\in C_f$. Then g is called a Meir-Keeler α-f-contractive map if for each $ϵ>0$, there exists a $\delta >0$ such that for all $x,y\in X$,

$$ϵ\le d(fx,fy)<ϵ+\delta \text{implies}\alpha (x,y)d(gx,gy)<ϵ.$$

(9)

Definition 14 Let f be a self-map of a metric space $(X,d)$ and $g\in C_f$. Then g is called a generalized Meir-Keeler α-f-contractive map if for each $ϵ>0$, there exists a $\delta >0$ such that for all $x,y\in X$,

$$ϵ\le M_g(f)(x,y)<ϵ+\delta \text{implies}\alpha (x,y)d(gx,gy)<ϵ,$$

(10)

where $M_g(f)(x,y)=max\{d(fx,fy),d(fx,gx),d(fy,gy),\frac{d(fx,gy)+d(fy,gx)}{2}\}$.

Lemma 15 Let f, g be continuous self-maps of a metric space $(X,d)$ such that $g\in C_f$. Assume g is a generalized Meir-Keeler α-f-contractive map such that $\alpha (x_n,x_{n+1})\ge 1$ for all n. Then $inf\{d(f{x}_n,f{x}_{n+1}):n=0,1,2,\dots \}=0$.

Proof Let $\sigma =inf\{d(f{x}_n,f{x}_{n+1}):n=0,1,2,\dots \}$ and $\sigma >0$. From the definition of the f-iteration of $x_0$ under g and from the fact that g is a generalized Meir-Keeler α-f-contractive map, for each n, we have

$$\begin{array}{rcl}d(f{x}_{n+1},f{x}_{n+2})& =& d(g{x}_n,g{x}_{n+1})\le \alpha (x_n,x_{n+1})d(g{x}_n,g{x}_{n+1})\\ <& max\{d(f{x}_n,f{x}_{n+1}),d(f{x}_n,g{x}_n),d(f{x}_{n+1},g{x}_{n+1}),\\ \frac{d(f{x}_n,g{x}_{n+1})+d(f{x}_{n+1},g{x}_n)}{2}\}\\ =& max\{d(f{x}_n,f{x}_{n+1}),d(f{x}_n,f{x}_{n+1}),d(f{x}_{n+1},f{x}_{n+2}),\frac{d(f{x}_n,f{x}_{n+2})+0}{2}\}\\ =& max\{d(f{x}_n,f{x}_{n+1}),\frac{d(f{x}_n,f{x}_{n+2})}{2}\}\\ \le & max\{d(f{x}_n,f{x}_{n+1}),\frac{d(f{x}_n,f{x}_{n+1})+d(f{x}_{n+1},f{x}_{n+2})}{2}\}.\end{array}$$

Hence, $d(f{x}_{n+1},f{x}_{n+2})<d(f{x}_n,f{x}_{n+1})$ and $\{d(f{x}_n,f{x}_{n+1})\}$ is monotone decreasing so that $\sigma ={lim}_{n\to \mathrm{\infty }}d(f{x}_n,f{x}_{n+1})$. From the assumption that g is a Meir-Keeler α-f-contractive map, for $ϵ=\sigma$, find $\delta >0$ such that (10) is satisfied. For the chosen δ, pick N so that $\sigma \le d(f{x}_n,f{x}_{n+1})<\sigma +\delta$. Noting that for $x=x_n$ and $y=x_{n+1}$, $M_g(f)(x,y)=d(f{x}_n,f{x}_{n+1})$, we by (10) conclude that $d(g{x}_n,g{x}_{n+1})\le \alpha (x_n,x_{n+1})d(g{x}_n,g{x}_{n+1})<\sigma$. But $d(g{x}_n,g{x}_{n+1})=d(f{x}_{n+1},f{x}_{n+2})<\sigma$, a contradiction. □

Theorem 16 Let f, g be continuous self-maps of a metric space $(X,d)$ such that $g\in C_f$. Assume $\alpha (x_n,x_m)\ge 1$ for all $m>n$. If g is a generalized Meir-Keeler α-f-contractive map such that α satisfies the condition (f-H): If $\{x_n\}$ is a sequence in X such that $\alpha (x_n,x_m)\ge 1$ for all $m>n$ and $f{x}_n\to z$, then $\alpha (f{x}_n,z)\ge 1$ and $\alpha (f{x}_n,fz)\ge 1$ for all n. Then f and g have a unique common fixed point.

Proof Let $x_0\in X$ for which its f-iteration under g satisfies the assumptions of the theorem. The proof will be divided into four steps.

• Step 1: By Lemma 15, $inf\{d(f{x}_n,f{x}_{n+1}):n=0,1,2,\dots \}=0$.

• Step 2: We find a coincidence point for f and g. That is to find a $z\in X$ such that $fz=gz$. If there exists an n such that $d(f{x}_n,f{x}_{n+1})=0$, then $f{x}_{n+1}=g{x}_n=f{x}_n$, and we are finished. Hence, we may assume that $d(f{x}_n,f{x}_{n+1})\ne 0$ for each n. We claim to show that $\{f{x}_n\}$ is Cauchy. Suppose not. Then there exists an $ϵ>0$ and a subsequence $\{f{x}_{n_i}\}$ of $\{f{x}_n\}$ such that $d(f{x}_{n_i},f{x}_{n_{i+1}})>2ϵ$. From (10), there exists a δ satisfying $0<\delta <ϵ$ for which (10) is true. Since ${lim}_{n\to \mathrm{\infty }}d(f{x}_n,f{x}_{n+1})$=0, there exists an N such that

  $$d(f{x}_m,f{x}_{m+1})<\frac{\delta }{6}\text{for all }m>N.$$

  Let $n_i\ge N$. We will show that there exists an integer j satisfying $n_i<j<n_{i+1}$ such that

  $$ϵ+\frac{\delta }{3}\le d(f{x}_{n_i},f{x}_j)<ϵ+\frac{2\delta }{3}.$$

  (11)

  First of all, there exist values of j such that $d(f{x}_{n_i},f{x}_j)\ge ϵ+\frac{\delta }{3}$. For example, choose $j=n_{i+1}$. The inequality is also true for $j=n_{i+1}-1$. If not, then $d(f{x}_{n_i},f{x}_j)<ϵ+\frac{\delta }{3}$ and hence

  $$\begin{array}{rcl}d(f{x}_{n_i},f{x}_{n_{i+1}})& \le & d(f{x}_{n_i},f{x}_{n_{i+1}}-1)+d(f{x}_{n_{i+1}}-1,f{x}_{n_{i+1}})\\ <& ϵ+\frac{\delta }{3}+\frac{\delta }{6}<2ϵ,\end{array}$$

  a contradiction. There are also values of j such that $d(f{x}_{n_i},f{x}_j)<ϵ+\frac{\delta }{3}$. For example, choose $j=n_i+1$ and $j=n_i+2$. Pick j to be the smallest integer greater than $n_i$ such that $d(f{x}_{n_i},f{x}_j)\ge ϵ+\frac{\delta }{3}$. Then $d(f{x}_{n_i},f{x}_i-1)<ϵ+\frac{\delta }{3}$, and hence

  $$d(f{x}_{n_i},f{x}_j)\le d(f{x}_{n_i},f{x}_j-1)+d(f{x}_j-1,f{x}_j)<ϵ+\frac{\delta }{3}+\frac{\delta }{6}<ϵ+\frac{2\delta }{3}.$$

  Thus (11) is established. Now, note that

  $$ϵ+\frac{\delta }{3}\le d(f{x}_{n_i},f{x}_j)\le max\{d(f{x}_{n_i},f{x}_j),d(f{x}_{n_i},g{x}_{n_i}),d(f{x}_j,g{x}_j),\frac{d(f{x}_{n_i},g{x}_j)+d(f{x}_j,g{x}_{n_i})}{2}\}.$$

  Then from the choice of j and the fact that $f{x}_{n_i}+1=g{x}_{n_i}$, $f{x}_j+1=g{x}_j$, we reach

  $$ϵ\le d(f{x}_{n_i},f{x}_j)<\delta +ϵ.$$

  Hence,

  $$d(f{x}_{n_i+1},f{x}_{j+1})=d(g{x}_{n_i},g{x}_j)\le \alpha (x_{n_i},x_j)d(g{x}_{n_i},g{x}_j)<ϵ.$$

  On the other hand,

  $$\begin{array}{rcl}d(f{x}_{n_i},f{x}_j)& \le & d(f{x}_{n_i},f_{n_i+1})+d(f_{n_i+1},f{x}_{j+1})+d(f{x}_{j+1},f{x}_j)\\ <& \frac{\delta }{6}+ϵ+\frac{\delta }{6}=ϵ+\frac{\delta }{3},\end{array}$$

  contradicting (11). Therefore, $\{f{x}_n\}$ is Cauchy hence convergent to $z\in X$. Since $ff{x}_n=fg{x}_{n-1}=gf{x}_{n-1}$, the continuity of f and g implies that $fz=gz$.

• Step 3: We show that $\eta =fz=gz$ is a common fixed point for f and g. Assume $f\eta \ne \eta$, then $f^{2}z\ne fz$ and by the help of the (f-H) condition, we have

  $$\begin{array}{rcl}d(\eta ,f\eta )& =& d(gz,fgz)=d(gz,gfz)\\ \le & d(gz,gf{x}_n)+d(gf{x}_n,gfz)\\ \le & \alpha (f{x}_n,z)d(gz,gf{x}_n)+\alpha (f{x}_n,fz)d(gf{x}_n,gfz)\\ <& max\{d(fz,ff{x}_n),d(fz,gz),d(ff{x}_n,gf{x}_n),\frac{d(fz,gf{x}_n)+d(ff{x}_n,gfz)}{2}\}\\ +max\{d(ff{x}_n,ffz),d(ff{x}_n,gf{x}_n),d(ffz,gfz),\frac{d(ff{x}_n,gfz)+d(ffz,gf{x}_n)}{2}\}.\end{array}$$

  If we let $n\to \mathrm{\infty }$ above and use continuity and commutativity of f and g, then we reach $d(\eta ,f\eta )<d(\eta ,f\eta )$ and hence $f\eta =\eta$. Moreover, $g\eta =gfz=f\eta =\eta$.

• Step 4: Uniqueness of the common fixed point. Assume $\eta =fz=gz$ is our common fixed point for f and g where $f{x}_n\to z$ and ω is another common fixed point. Then, by the (f-H) condition, we have

  $$\begin{array}{rcl}d(\eta ,\omega )& =& d(g\eta ,\omega )\le d(g\eta ,gf{x}_n)+d(gf{x}_n,\omega )\\ \le & \alpha (\eta ,f{x}_n)d(g\eta ,gf{x}_n)+d(gf{x}_n,\omega )\\ <& max\{d(f\eta ,ff{x}_n),d(f\eta ,g\eta ),d(ff{x}_n,gf{x}_n),\frac{d(f\eta ,gf{x}_n)+d(ff{x}_n,g\eta )}{2}\}.\end{array}$$

  If we let $n\to \mathrm{\infty }$ above and use the continuity of f and g, we conclude that $d(\eta ,\omega )<d(\eta ,\omega )$ and hence $\eta =\omega$.

   □

Remark 17 Theorem 16 has been proved for commuting maps. It would be interesting to extend it for weakly commuting and compatible mappings and so forth. For example, can we extend the results in [20–22] to α-type contractions?

4 Application to coupled α-Meir-Keeler fixed points

Let $F:X\times X\to X$ be a mapping. We say that $(x,y)\in X\times X$ is a coupled fixed point of F if $F(x,y)=x$ and $F(y,x)=y$. If we define $T:X\times X\to X\times X$ by $T(x,y)=(F(x,y),F(y,x))$, then clearly $(x,y)$ is a coupled fixed point of F if and only if $(x,y)$ is a fixed point of T. If $(x_0,y_0)\in X\times X$, then the F-orbit of $(x_0,y_0)$ means the orbit $\{(x_n,y_n):n=0,1,2,\dots \}$, where $(x_{n+1},y_{n+1})=T(x_n,y_n)$.

If $(X,d)$ is a metric space, then $\rho :X\times X\to \mathbb{R}$ defined by $\rho ((x,y),(u,v))=d(x,u)+d(y,v)$ is a metric on $X\times X$.

Theorem 18 Let $(X,d)$ be a complete metric space and $F:X\times X\to X$ be a continuous mapping. Also, let $\alpha :X^2\times X^2\to [0,\mathrm{\infty })$ be a mapping. Assume the following:

• 1. For all $(x,y),(u,v)\in X\times X$, we have

  $$\alpha ((x,y),(u,v))\ge 1\text{implies}\alpha ((F(x,y),F(y,x)),(F(u,v),F(v,u)))\ge 1.$$

  Also, assume there exists $(x_0,y_0)\in X\times X$ such that $\alpha ((F(y_0,x_0),F(x_0,y_0)),(y_0,x_0))\ge 1$ and $\alpha ((x_0,y_0),(F(x_0,y_0),F(y_0,x_0)))\ge 1$;

• 2. For each $ϵ>0$, there exists $\delta >0$ such that

  $$ϵ\le \frac{1}{2}[d(x,u)+d(y,v)]<\delta +ϵ\text{implies}\alpha ((x,y),(u,v))d(F(x,y),F(u,v))<ϵ.$$

  Then the sequence ${\rho }_n=\rho ((x_n,y_n),(x_{n+1},y_{n+1}))$ is monotone decreasing. If, moreover, we assume that

• 3. on the F-orbit of $(x_0,y_0)$, we have $\alpha ((x_n,y_n),(x_j,y_j))\ge 1$ and $\alpha ((y_j,x_j),(y_n,x_n))\ge 1$ for all n, j.

Then either (1) F has a coupled fixed point in the F-orbit $\{(x_n,y_n)\}$ of $(x_0,y_0)$ or (2) F has a coupled fixed point $(p,q)$ and $lim\rho (x_n,y_n)=(p,q)$. If, moreover, we assume that the following condition (H) holds: If $\{(x_n,y_n)\}$ is a sequence in $X\times X$ such that $\alpha ((x_n,y_n),(x_{n+1},y_{n+1}))\ge 1$ for all n and $d(x_n,x)\to 0$, $d(y_n,y)\to 0$, then $\alpha ((x_n,y_n),(x,y))\ge 1$ and $\alpha ((y,x),(y_n,x_n))\ge 1$ for all n, then uniqueness of the coupled fixed point is obtained.

Proof The proof will follow by applying Corollary 9, with $f=T$ as above, to the metric space $(X\times X,\rho )$. The controlling function will be $\beta :X^2\times X^2\to [0,\mathrm{\infty })$ given by

$$\beta ((x,y),(u,v))=min\{\alpha ((x,y),(u,v)),\alpha ((y,x),(v,u))\}.$$

In fact, if $ϵ>0$ is given, then by assumption (2), find ${\delta }^{\mathrm{\prime }}>0$ such that

$$\frac{ϵ}{2}\le \frac{1}{2}[d(x,u)+d(y,v)]<{\delta }^{\mathrm{\prime }}+\frac{ϵ}{2}\text{implies}\alpha ((x,y),(u,v))d(F(x,y),F(u,v))<\frac{ϵ}{2}.$$

Let $\delta =2{\delta }^{\mathrm{\prime }}$ and assume $ϵ\le \rho ((x,y),(u,v))<\delta +ϵ$. Then

$$\frac{ϵ}{2}\le \frac{1}{2}[d(x,u)+d(y,v)]<{\delta }^{\mathrm{\prime }}+\frac{ϵ}{2}$$

and

$$\frac{ϵ}{2}\le \frac{1}{2}[d(v,u)+d(u,x)]<{\delta }^{\mathrm{\prime }}+\frac{ϵ}{2}.$$

Hence,

$$\alpha ((x,y),(u,v))d(F(x,y),F(u,v))<\frac{ϵ}{2}$$

and

$$\alpha ((v,u),(y,x))d(F(y,x),F(v,u))<\frac{ϵ}{2},$$

which leads to

$$\beta ((x,y),(u,v))\rho (T(x,y),T(u,v))<ϵ.$$

 □