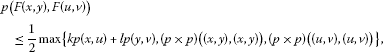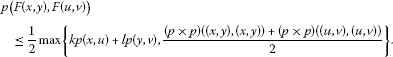Coupled fixed point theorems for partially contractive mappings

Abstract

Recently, some authors have started to generalize fixed point theorems for contractive mappings in a class of generalized metric spaces in which the self-distance need not be zero. These spaces, partial metric spaces, were first introduced by Matthews in 1994. The proved fixed point theorems have been obtained for mappings satisfying contraction type conditions empty of the self-distance. In this article, we prove some coupled fixed point theorems for mappings satisfying contractive conditions allowing the appearance of self-distance terms. These partially contractive mappings do reflect the structure of the partial metric space, and hence their coupled fixed theorems generalize the previously obtained by (Aydi in Int. J. Math. Sci. 2011:Article ID 647091, 2011). Some examples are given to support our claims.

MSC:47H10, 54H25.

1 Introduction and preliminaries

The Banach contraction mapping principle is considered to be the soul of many extended fixed point theorems. It has widespread applications in many branches of mathematics, engineering and computer science. During the last decades many authors were able to generalize this principle [1–4]. After the appearance of partial metric spaces as a place for distinct research work into flow analysis, non-symmetric topology and domain theory [5, 6], many authors started to generalize this principle to these spaces (see [7–16]. However, the contraction type conditions used in those generalizations do not reflect the structure of a partial metric space apparently. Later, the authors in [17] proved a more reasonable contraction principle in the partial metric space in which they used self-distance terms. On the other hand, the theory of coupled fixed point theorems has recently attracted some authors (see [18–20]). Also, Meir-Keeler type common and tripled fixed point theorems have been recently considered over partial metric spaces [21, 22]. In this article, we prove a coupled partial contraction principle generalizing the recently published coupled fixed point theorems in [18]. An example is presented to show that our coupled partial contraction principle is worthy of investigation.

A partial metric space (PMS) (see, e.g., [5, 6]) is a pair $(X,p:X\times X\to {\mathbb{R}}^{+})$ (where ${\mathbb{R}}^{+}$ denotes the set of all nonnegative real numbers) such that

(P1) $p(x,y)=p(y,x)$ (symmetry)

(P2) If $0\le p(x,x)=p(x,y)=p(y,y)$ then $x=y$ (equality)

(P3) $p(x,x)\le p(x,y)$ (small self-distances)

(P4) $p(x,z)+p(y,y)\le p(x,y)+p(y,z)$ (triangularity)

for all $x,y,z\in X$.

For a partial metric p on X, the function $d_p:X\times X\to {\mathbb{R}}^{+}$ given by

$$d_p(x,y)=2p(x,y)-p(x,x)-p(y,y)$$

(1)

is a (usual) metric on X. Each partial metric p on X generates a $T_0$ topology ${\tau }_p$ on X with a base of the family of open p-balls $\{B_p(x,\epsilon ):x\in X,\epsilon >0\}$, where $B_p(x,\epsilon )=\{y\in X:p(x,y)<p(x,x)+\epsilon \}$ for all $x\in X$ and $\epsilon >0$.

Definition 1 (see, e.g., [5, 6, 13])

• (i) A sequence $\{x_n\}$ in a PMS $(X,p)$ converges to $x\in X$ if and only if $p(x,x)={lim}_{n\to \mathrm{\infty }}p(x,x_n)$;

• (ii) A sequence $\{x_n\}$ in a PMS $(X,p)$ is called Cauchy if and only if ${lim}_{n,m\to \mathrm{\infty }}p(x_n,x_m)$ exists (and is finite);

• (iii) A PMS $(X,p)$ is said to be complete if every Cauchy sequence $\{x_n\}$ in X converges, with respect to ${\tau }_p$, to a point $x\in X$ such that $p(x,x)={lim}_{n,m_{\to }\mathrm{\infty }}p(x_n,x_m)$;

• (iv) A mapping $f:X\to X$ is said to be continuous at $x_0\in X$, if for every $\epsilon >0$, there exists $\delta >0$ such that $f(B_p(x_0,\delta ))\subset B_p(f(x_0),\epsilon )$.

Lemma 2 (see, e.g., [5, 6, 13])

• (A) A sequence $\{x_n\}$ is Cauchy in a PMS $(X,p)$ if and only if $\{x_n\}$ is Cauchy in a metric space $(X,d_p)$;

• (B) A PMS $(X,p)$ is complete if and only if the metric space $(X,d_p)$ is complete. Moreover,

  $$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x,x_n)=0\iff p(x,x)=\underset{n\to \mathrm{\infty }}{lim}p(x,x_n)=\underset{n,m_{\to }\mathrm{\infty }}{lim}p(x_n,x_m).$$

  (2)

A sequence $\{x_n\}$ is called 0-Cauchy [17] if ${lim}_{m,n}p(x_n,x_m)=0$. The partial metric space $(X,p)$ is called 0-complete [17, 23] if every 0-Cauchy sequence in x converges to a point $x\in X$ with respect to p and $p(x,x)=0$. Clearly, every complete partial metric space is 0-complete. The converse need not be true.

Example 3 (see [17])

Let $X=\mathbb{Q}\cap [0,\mathrm{\infty })$ with the partial metric $p(x,y)=max\{x,y\}$. Then $(X,p)$ is a 0-complete partial metric space which is not complete.

Let ${\rho }_p=inf\{p(x,y):x,y\in X\}$ and define $X_p=\{x\in X:p(x,x)={\rho }_p\}$.

The following theorem was presented in [17].

Theorem 4 Let $(X,p)$ be a complete metric space, $\alpha \in [0,1)$ and $T:X\to X$ a given mapping. Suppose that for each $x,y\in X$ the following condition holds:

$$p(x,y)\le max\{\alpha p(x,y),p(x,x),p(y,y)\}.$$

Then

• (1) the set $X_p$ is nonempty;

• (2) there is a unique $u\in X_p$ such that $Tu=u$;

• (3) for each $x\in X_p$ the sequence ${\{T^{n}x\}}_{n\ge 1}$ converges to u with respect to the metric $d_p$.

If $(X,p)$ is a partial metric space, then clearly $(p\times p):X\times X\to \mathbb{R}$ defined by $(p\times p)((x,y),(u,v))=p(x,u)+p(y,v)$ is a partial metric, and hence $(X\times X,(p\times p))$ is a partial metric space. Clearly, if $(X,p)$ is complete (0-complete) then so is $(X\times X,(p\times p))$. The minimum self partial distance in $(X\times X,(p\times p))$ is defined by

$${\rho }_{p\times p}:=inf\{(p\times p)((x,y),(x,y))=p(x,x)+p(y,y):x,y\in X\}.$$

The set of all points in $X\times X$ with self partial distance ${\rho }_{p\times p}$ is denoted by

$${(X\times X)}_{p\times p}=\{(x,y)\in X\times X:(p\times p)((x,y),(x,y))={\rho }_{p\times p}\}.$$

Example 5 Let $X=[0,1]$ and provide X with the partial metric $p(x,y)=|x-y|$ if both $x,y\in [0,1)$ and $p(x,y)=max\{x,y\}$ otherwise. Then clearly $(X,p)$ is a complete partial metric space, ${\rho }_{p\times p}=0$ and ${(X\times X)}_{p\times p}=[0,1)\times [0,1)$.

Definition 6 Let $(X,p)$ be a partial metric space and $F:X\times X\to X$ be a mapping. Then F is called

• (a) partially contractive if there exist constants $0\le k,l<1$ such that for all $x,y,u,v\in X$,

  

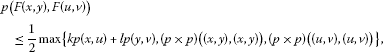  (3)

• (b) strong partially contractive if there exist constants $0\le k,l<1$ such that for all $x,y,u,v\in X$,

  

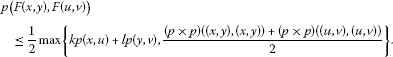  (4)

Aydi [18] proved the following coupled fixed point theorems in partial metric spaces:

Theorem 7 Let $(X,p)$ be a complete partial metric space. Suppose that the mapping $F:X\times X\to X$ satisfies the following contractive condition for all $x,y,u,v\in X$:

$$p(F(x,y),F(u,v))\le kp(x,u)+lp(y,v),$$

where $0\le k,l<1$ with $k+l<1$. Then F has a unique coupled fixed point. That is, there exists unique $(x,y)\in X\times X$ such that $F(x,y)=x$ and $F(y,x)=y$.

Theorem 8 Let $(X,p)$ be a complete partial metric space. Suppose that the mapping $F:X\times X\to X$ satisfies the following contractive condition for all $x,y,u,v\in X$:

$$p(F(x,y),F(u,v))\le kp(F(x,y),x)+lp(F(u,v),u),$$

where $0\le k,l<1$ with $k+l<1$. Then F has a unique coupled fixed point.

2 Main results

Theorem 9 Let $(X,p)$ be a complete partial metric space and $F:X\times X\to X$ be a partially contractive mapping. Then

• (a) ${(X\times X)}_{p\times p}\ne \mathrm{\varnothing }$,

• (b) there exists a unique $(u,v)\in {(X\times X)}_{p\times p}$ such that

  $$F(u,v)=u\mathit{\text{and}}F(v,u)=v;$$

  (5)

• (c) for each $(x_0,y_0)\in {(X\times X)}_{p\times p}$ the sequence $\{(x_n,y_n)\}\in X\times X$ defined by

  $$x_1=F(x_0,y_0),y_1=F(y_0,x_0),x_{n+1}=F(x_n,y_n),y_{n+1}=F(y_n,x_n),n\ge 1,$$

converges to $(u,v)$ with respect to $d_p\times d_p$. That is

$$\underset{n\to \mathrm{\infty }}{lim}(d_p\times d_p)((x_n,y_n),(u,v))=\underset{n\to \mathrm{\infty }}{lim}(d_p(x_n,u)+d_p(y_n,v))=0.$$

Proof If $(x_0,y_0)\in X\times X$, define the sequence $\{(x_n,y_n)\}\in X\times X$ by

$$x_1=F(x_0,y_0),y_1=F(y_0,x_0),x_{n+1}=F(x_n,y_n),y_{n+1}=F(y_n,x_n),n\ge 1.$$

We divide the proof of the claim (a) into the following steps:

Step I: The sequence $\{(p\times p)((x_n,y_n)(x_n,y_n))\}=\{p(x_n,x_n)+p(y_n,y_n)\}$ is non-increasing. From the condition (3) we have

$$\begin{array}{rcl}{T}_n& =& p(F(x_n,y_n),F(x_n,y_n))+p(F(y_n,x_n),F(y_n,x_n))\\ \le & \frac{1}{2}[p(x_n,x_n)+p(y_n,y_n)]+\frac{1}{2}[p(x_n,x_n)+p(y_n,y_n)]\\ =& p(x_n,x_n)+p(y_n,y_n)=(p\times p)((x_n,y_n),(x_n,y_n)),\end{array}$$

where $T_n=(p\times p)((x_{n+1},y_{n+1}),(x_{n+1},y_{n+1}))$. As a result of Step I, there exists $r(x_0,y_0)\ge 0$ such that

$$\underset{n\to \mathrm{\infty }}{lim}(p\times p)((x_n,y_n),(x_n,y_n))=\underset{n}{inf}(p\times p)((x_n,y_n),(x_n,y_n))=r(x_0,y_0).$$

Step II: For each $n\ge 0$, we show that

(6)

where $\tau =max\{k,l\}$. We follow by induction. For $n=0,1$, it is clear. Assume (6) is true for $n\le r$, and let us prove (6) for $n=r+1\ge 2$. Then by the help of (3), the triangle inequality and Step I, we have

$$\begin{array}{rcl}E& =& (p\times p)((x_{r+1},y_{r+1}),(x_0,y_0))\\ \le & p(x_{r+1},x_1)+p(x_1,x_0)+p(y_{r+1},y_1)+p(y_1,y_0)\\ =& p(x_1,x_0)+p(y_1,y_0)+p(F(x_r,y_r),F(x_0,y_0))+p(F(y_r,x_r),F(y_0,x_0))\\ \le & (p\times p)((x_1,y_1),(x_0,y_0))\\ +\frac{1}{2}max\{kp(x_r,x_0)+lp(y_r,y_0),(p\times p)((x_0,y_0),(x_0,y_0))\}\\ +\frac{1}{2}max\{lp(x_r,x_0)+kp(y_r,y_0),(p\times p)((x_0,y_0),(x_0,y_0))\}\\ \le & (p\times p)((x_1,y_1),(x_0,y_0))\\ +max\{\tau (p\times p)((x_r,y_r),(x_0,y_0)),(p\times p)((x_0,y_0),(x_0,y_0))\}\\ \le & (p\times p)((x_1,y_1),(x_0,y_0))\\ +max\{\tau M(x_0,y_0),(p\times p)((x_0,y_0),(x_0,y_0))\}\le M(x_0,y_0),\end{array}$$

where $E=p(x_{r+1},x_0)+p(y_{r+1},y_0)$.

Step III: We show that

$$\underset{m,n\to \mathrm{\infty }}{lim}(p\times p)((x_n,y_n),(x_m,y_m))=\underset{m,n\to \mathrm{\infty }}{lim}[p(x_n.x_m)+p(y_n,y_m)]=r(x_0,y_0).$$

(7)

Let $ϵ>0$. Choose $n_0$ such that $(p\times p)((x_{n_0},y_{n_0}),(x_{n_0},y_{n_0}))<r(x_0,y_0)+ϵ$ and $2M(x_0,y_0){\tau }^{n_0}<r(x_0,y_0)+ϵ$. Then for $m,n\ge 2n_0$, we have

$$\begin{array}{rcl}S& =& p(F(x_{n-1},y_{n-1}),F(x_{m-1},y_{m-1}))+p(F(y_{n-1},x_{n-1}),F(y_{m-1},x_{m-1}))\\ \le & \frac{1}{2}max\{kp(x_{n-1},x_{m-1})+lp(y_{n-1},y_{m-1}),(p\times p)((x_{n-1},y_{n-1}),\\ (x_{n-1},y_{n-1})),(p\times p)((x_{m-1},y_{m-1}),(x_{m-1},y_{m-1}))\}\\ +\frac{1}{2}max\{lp(x_{n-1},x_{m-1})+kp(y_{n-1},y_{m-1}),(p\times p)((x_{n-1},y_{n-1}),\\ (x_{n-1},y_{n-1})),(p\times p)((x_{m-1},y_{m-1}),(x_{m-1},y_{m-1}))\}\\ \le & max\{\tau [p(x_{n-1},x_{m-1})+p(y_{n-1},y_{m-1})],(p\times p)((x_{n-1},y_{n-1}),\\ (x_{n-1},y_{n-1})),(p\times p)((x_{m-1},y_{m-1}),(x_{m-1},y_{m-1}))\}\le \cdots \\ \le & max\{{\tau }^{n_0}[p(x_{n-n_0},x_{m-n_0})+p(y_{n-n_0},y_{m-n_0})],(p\times p)((x_{n-n_0},y_{n-n_0}),\\ (x_{n-n_0},y_{n-n_0})),(p\times p)((x_{m-n_0},y_{m-n_0}),(x_{m-n_0},y_{m-n_0}))\}\\ \le & max\{r(x_0,y_0)+ϵ,r(x_0,y_0)+ϵ,2M(x_0,y_0){\tau }^{n_0}\}\le r(x_0,y_0)+ϵ,\end{array}$$

(8)

where $S=p(x_n,x_m)+p(y_n,y_m)$. On the other hand, (P3) implies $r(x_0,y_0)-ϵ\le p(x_n,x_n)+p(y_n,y_n)\le p(x_n,x_m)+p(y_n,y_m)$ and so (7) is obtained.

As a result of (7) and completeness of $(X,p)$, there exists $(x_0^{.},y_0^{.})\in X\times X$ such that

$$\begin{array}{rcl}r(x_0,y_0)& =& \underset{m,n\to \mathrm{\infty }}{lim}(p\times p)((x_n,y_n),(x_m,y_m))\\ =& \underset{n\to \mathrm{\infty }}{lim}(p\times p)((x_n,y_n),(x_0^{.},y_0^{.}))=(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.})).\end{array}$$

(9)

Step IV: We show that for each $n\ge 0$ the following holds:

$$(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.}))=(p\times p)((x_0^{.},y_0^{.}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.}))).$$

(10)

First, note that by (P3) applied to p or $p\times p$, we have

$$(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.}))\le (p\times p)((x_0^{.},y_0^{.}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.}))).$$

(11)

By the help of the triangle inequality applied to p or $p\times p$ , for each $n\ge 0$, we have

$$\begin{array}{rcl}T& \le & (p\times p)((x_0^{.},y_0^{.}),(x_{n+1},y_{n+1}))\\ +(p\times p)((x_{n+1},y_{n+1}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))\\ -(p\times p)((x_{n+1},y_{n+1}),(x_{n+1},y_{n+1})),\end{array}$$

(12)

where $T=(p\times p)((x_0^{.},y_0^{.}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))$. By the condition (3) and definition of $p\times p$, we have

$$\begin{array}{rcl}L& \le & \frac{1}{2}max\{kp(x_n,x_0^{.})+lp(y_n,y_0^{.}),\\ (p\times p)((x_n,y_n),(x_n,y_n)),(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.}))\}\\ +\frac{1}{2}max\{kp(y_n,y_0^{.})+lp(x_n,x_0^{.}),\\ (p\times p)((y_n,x_n),(y_n,x_n)),(p\times p)((y_0^{.},x_0^{.}),(y_0^{.},x_0^{.}))\}\\ \le & max\{\tau [p(x_n,x_0^{.})+p(y_n,y_0^{.})],\\ (p\times p)((x_n,y_n),(x_n,y_n)),(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.}))\},\end{array}$$

where $L=(p\times p)((x_{n+1},y_{n+1}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))$. Without loss of generality (by passing to subsequence if necessary), we may assume that for each $n\ge 0$, we have one of the following:

$$(p\times p)((x_{n+1},y_{n+1}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))\le \tau [p(x_n,x_0^{.})+p(y_n,y_0^{.})],$$

or

$$(p\times p)((x_{n+1},y_{n+1}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))\le (p\times p)((x_n,y_n),(x_n,y_n)),$$

or

$$(p\times p)((x_{n+1},y_{n+1}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))\le (p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.})).$$

Substituting each of these cases in (12), letting $n\to \mathrm{\infty }$ and using (9) together with (11), we arrive at (10).

Step V: We prove that ${(X\times X)}_{p\times p}\ne \mathrm{\varnothing }$.

For each $k\in \mathbb{N}$, pick $(x_k,y_k)\in X\times X$ with

$$(p\times p)((x_k,y_k),(x_k,y_k))<{\rho }_{p\times p}+\frac{1}{k}.$$

(13)

We show that

$$\underset{m,n\to \mathrm{\infty }}{lim}(p\times p)((x_n^{.},y_n^{.}),(x_m^{.},y_m^{.}))={\rho }_{p\times p}.$$

(14)

Given $ϵ>0$ put $n_0=[\frac{3}{ϵ(1-\tau )}]+1$. If $k\ge n_0$ then by (3) we have

$$\begin{array}{rcl}{\rho }_{p\times p}& \le & (p\times p)((F(x_k^{.},y_k^{.}),F(y_k^{.},x_k^{.})),(F(x_k^{.},y_k^{.}),F(y_k^{.},x_k^{.})))\\ =& p(F(x_k^{.},y_k^{.}),F(x_k^{.},y_k^{.}))+p(F(y_k^{.},x_k^{.}),F(y_k^{.},x_k^{.}))\\ \le & p(x_k^{.},x_k^{.})+p(y_k^{.},y_k^{.})\\ =& (p\times p)((x_k^{.},y_k^{.}),(x_k^{.},y_k^{.}))=r(x_k,y_k)\\ \le & (p\times p)((x_k,y_k),(x_k,y_k))<{\rho }_{p\times p}+\frac{1}{k}\\ \le & {\rho }_{p\times p}+\frac{1}{n_0}<{\rho }_{p\times p}+\frac{ϵ(1-\tau )}{3}.\end{array}$$

(15)

Hence, we conclude that for all $k\ge n_0$,

$$\begin{array}{rcl}{U}_k& :=& (p\times p)((x_k^{.},y_k^{.}),(x_k^{.},y_k^{.}))-(p\times p)((F(x_k^{.},y_k^{.}),F(y_k^{.},x_k^{.})),(F(x_k^{.},y_k^{.}),F(y_k^{.},x_k^{.})))\\ \le & \frac{ϵ(1-\tau )}{3}+({\rho }_{p\times p}-(p\times p)((F(x_k^{.},y_k^{.}),F(y_k^{.},x_k^{.})),(F(x_k^{.},y_k^{.}),F(y_k^{.},x_k^{.}))))\\ <& \frac{ϵ(1-\tau )}{3}\end{array}$$

(16)

and

$$(p\times p)((x_k^{.},y_k^{.}),(x_k^{.},y_k^{.}))\le {\rho }_{p\times p}+\frac{ϵ(1-\tau )}{3}.$$

(17)

Now, if $m,n\ge n_0$, then by the triangle inequality applied to $(p\times p)$, Step IV and (3), we have

(18)

Hence, using (16) and (17), we obtain

$$\begin{array}{rcl}{\rho }_{p\times p}& \le & (p\times p)((x_n^{.},y_n^{.}),(x_m^{.},y_m^{.}))\\ \le & max\{\frac{2ϵ}{3},\frac{2ϵ(1-\tau )}{3}+(p\times p)((x_n^{.},y_n^{.}),(x_n^{.},y_n^{.})),\\ \frac{2ϵ(1-\tau )}{3}+(p\times p)((x_m^{.},y_m^{.}),(x_m^{.},y_m^{.}))\}\\ \le & max\{\frac{2ϵ}{3},ϵ(1-\tau )+{\rho }_{p\times p}\}\\ <& {\rho }_{p\times p}+ϵ.\end{array}$$

(19)

This shows (14) and so $\{(x_n^{.},y_n^{.})\}$ is Cauchy in the complete partial metric space $(X\times X,p\times p)$. Therefore, there exists $(x,y)\in X\times X$ such that

(20)

In particular $(x,y)\in {(X\times X)}_{p\times p}$ and so ${(X\times X)}_{p\times p}\ne \mathrm{\varnothing }$.

Now, let $(x_0,y_0)\in {(X\times X)}_{p\times p}$ be arbitrary. Then by (9), (P3) applied to $p\times p$ and (10), we have

$$\begin{array}{rcl}{\rho }_{p\times p}& \le & (p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.}))\\ \le & (p\times p)((x_0^{.},y_0^{.}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))=(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y^{.}))=r(x_0,y_0)\\ \le & (p\times p)((x_0,y_0),(x_0,y_0))={\rho }_{p\times p}.\end{array}$$

(21)

Therefore, (P2) applied to $p\times p$ implies that

$$(p\times p)((x_0^{.},y_0^{.}),(x_0^{.},y_0^{.}))=(p\times p)((x_0^{.},y_0^{.}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))$$

and so $(x_0^{.},y_0^{.})$ is a coupled fixed point of F. Clearly, (9) implies that $\{(x_n,y_n)\}$ converges to the coupled fixed point $(x_0^{.},y_0^{.})$ with respect to $d_p\times d_p$ which proves (c). To complete the proof of (b), assume $(x,y)\in {(X\times X)}_{p\times p}$ and $(u,v)\in {(X\times X)}_{p\times p}$ are both coupled fixed points of F. Then by (3) we have

$$\begin{array}{rcl}(p\times p)((x,y),(u,v))& =& (p\times p)((F(x,y),F(y,x)),(F(u,v),F(v,u)))\\ \le & max\{\tau (p\times p)((x,y),(u,v)),(p\times p)((x,y),(x,y)),\\ (p\times p)((u,v),(u,v))\}.\end{array}$$

(22)

From which it follows either $(p\times p)((x,y),(u,v))\le \tau (p\times p)((x,y),(u,v))$ and so $(p\times p)((x,y),(u,v))=0$ implies that $(x,y)=(u,v)$, or ${\rho }_{p\times p}\le (p\times p)((x,y),(u,v))\le (p\times p)((x,y),(x,y))=(p\times p)((u,v),(u,v))={\rho }_{p\times p}$, and hence (P2) applied to $p\times p$ implies $(x,y)=(u,v)$. □

Remark 10 Although Theorem 9 does not imply the uniqueness of the fixed point, it is easy to see that, under the assumptions made, if $(x,y)$ and $(u,v)$ are both coupled fixed points for F satisfying $(p\times p)((x,y),(x,y))=(p\times p)((u,v),(u,v))$, then $(x,y)=(u,v)$. If the partially contractive condition (3) is replaced by the somewhat stronger condition below, the uniqueness of the coupled fixed point is guaranteed.

Theorem 11 Let $(X,p)$ be a complete partial metric space, $0\le k,l<1$ and $F:X\times X\to X$ be a strong partially contractive mapping. Then there exists a unique coupled fixed point $(x,y)$. Furthermore, $(x,y)\in {(X\times X)}_{p\times p}$ and for each $(x_0,y_0)\in {(X\times X)}_{p\times p}$, the sequence $\{(x_n,y_n)\}\in X\times X$ defined by

$$x_1=F(x_0,y_0),y_1=F(y_0,x_0),x_{n+1}=F(x_n,y_n),y_{n+1}=F(y_n,x_n),n\ge 1,$$

converges to $(x,y)$ with respect to $d_p\times d_p$. That is

$$\underset{n\to \mathrm{\infty }}{lim}(d_p\times d_p)((x_n,y_n),(x,y))=\underset{n\to \mathrm{\infty }}{lim}(d_p(x_n,x)+d_p(y_n,y))=0.$$

Proof By Theorem 9, we only need to prove the uniqueness of the coupled fixed point. If $(x,y)$ and $(u,v)$ are two coupled fixed points, then

$$\begin{array}{rcl}G& =& p(x,u)+p(y,v)=p(F(x,y),F(u,v))+p(F(y,x),F(v,u))\\ \le & \frac{1}{2}max\{kp(x,u)+lp(y,v),\frac{(p\times p)((x,y),(x,y))+(p\times p)((u,v),(u,v))}{2}\}\\ +\frac{1}{2}max\{kp(x,u)+lp(y,v),\frac{(p\times p)((x,y),(x,y))+(p\times p)((u,v),(u,v))}{2}\}\\ \le & max\{\tau (p(x,u)+p(y,v)),\frac{(p\times p)((x,y),(x,y))+(p\times p)((u,v),(u,v))}{2}\},\end{array}$$

(23)

where $G=(p\times p)((x,y),(u,v))$ and $\tau =max\{k,l\}$. From (23) we distinguish the following cases:

Case 1: If $(p\times p)((x,y),(u,v))\le \tau (p(x,u)+p(y,v))=\tau (p\times p)((x,y),(u,v))$, then $(p\times p)((x,y),(u,v))=0$ and so $(x,y)=(u,v)$.

Case 2: If $(p\times p)((x,y),(u,v))\le \frac{(p\times p)((x,y),(x,y))+(p\times p)((u,v),(u,v))}{2}$, then $(d_p\times d_p)((x,y),(u,v))=0$ and so $(x,y)=(u,v)$. □

As a corollary, we obtain the already mentioned result [18] stated in Theorem 7. As well, let us remark that the result of Aydi in Theorem 7 is valid also for 0-complete partial metric spaces.

Corollary 12 Let $(X,p)$ be a 0-complete partial metric space. Suppose that the mapping $F:X\times X\to X$ satisfies the following contractive condition for all $x,y,u,v\in X$:

$$p(F(x,y),F(u,v))\le kp(x,u)+lp(y,v),$$

(24)

where $0\le k,l<1$ with $k+l<1$. Then F has a unique coupled fixed point $(u,v)$ such that $(p\times p)((u,v),(u,v))=0$. Also for each $(x_0,y_0)\in X\times X$ the sequence $\{(x_{n+1},y_{n+1})\}$ converges to $(u,v)$ with respect to the metric $d_p\times d_p$.

Proof The condition (24) implies that $(p\times p)((x_{n+1},y_{n+1}),(x_{n+1},y_{n+1}))\le {(k+l)}^n(p\times p)((x_0,y_0),(x_0,y_0))$, which, in turn, by (9) implies $(p\times p)((x_0^{.},y_0^{.}))=0$. But then by (10) we have $(p\times p)((x_0^{.},y_0^{.}),(F(x_0^{.},y_0^{.}),F(y_0^{.},x_0^{.})))=0$ so the $d_p\times d_p$-limit of the sequence $\{(x_{n+1},y_{n+1})\}$ is actually the unique coupled fixed point $(x_0^{.},y_0^{.})$. □

Example 13 Define $p:[0,1]\times [0,1]\to [0,1]$ by $p(x,y)=max\{x,y\}$. Then $([0,1],p)$ is a complete partial metric space. Let $F:[0,1]\times [0,1]\to [0,1]$ be defined by

$$F(x,y)=\frac{|x-y|}{2}.$$

Then we have

• (a) There are no $0\le k,l<1$ with $k+l<1$ such that $p(F(x,y),F(u,v))\le kp(x,u)+lp(y,v)$, for all $x,y,u,v\in [0,1]$. That is, F does not verify the assumptions of Theorem 7. Indeed, if we assume that there exist $0\le k,l<1$ with $k+l<1$ such that for all $x,y,u,v\in X=[0,1]$, we have

  $$p(F(x,y),F(u,v))\le kp(x,u)+lp(y,v),$$

then

$$p(F(1,0),F(0,0))=\frac{1}{2}\le kp(1,0)+lp(0,0)=k,$$

(25)

and

$$p(F(0,1),F(0,0))=\frac{1}{2}\le kp(0,0)+lp(1,0)=l,$$

(26)

then we have $k+l\ge 1$, which is a contradiction.

• (b) There are no $0\le k,l<1$ with $k+l<1$ such that $p(F(x,y),F(u,v))\le kp(F(x,y),x)+lp(F(u,v),u)$. That is, F does not verify the assumptions of Theorem 8. Indeed, if we assume that there exist $0\le k,l<1$ with $k+l<1$ such that for all $x,y,u,v\in X=[0,1]$, we have

  $$p(F(x,y),F(u,v))\le kp(F(x,y),x)+lp(F(u,v),u).$$

  (27)

Then we conclude that

$$p(F(0,1),F(0,0))=\frac{1}{2}\le kp(\frac{1}{2},0)+p(0,0)=\frac{k}{2}<\frac{1}{2},$$

which is a contradiction.

• (c) F is partially contractive. That is F verifies the assumptions of Theorem 9. Hence, it has the coupled fixed point $(0,0)$. The condition (3) is clearly satisfied since $|x-y|\le x+y$ for all $x,y\in X=[0,1]$.

• (d) Note that ${(X\times X)}_{p\times p}=\{(0,0)\}$ and hence the coupled Picard sequence $\{(x_n,y_n)\}$ converges for $(x_0,y_0)=(0,0)$ and for $(x_0,y_0)\in (X\times X)\mathrm{\setminus }\{(0,0)\}$ may converge or not depending on the particular choice of $(x_0,y_0)$.

• (e) If F is replaced by $H(x,y)=\frac{|x-y|}{4}$, then it is strong partially contractive, and hence by Theorem 11, we guarantee the uniqueness of the coupled fixed point $(0,0)$.