Solving systems of nonlinear matrix equations involving Lipshitzian mappings

Abstract

In this study, both theoretical results and numerical methods are derived for solving different classes of systems of nonlinear matrix equations involving Lipshitzian mappings.

2000 Mathematics Subject Classifications: 15A24; 65H05.

1 Introduction

Fixed point theory is a very attractive subject, which has recently drawn much attention from the communities of physics, engineering, mathematics, etc. The Banach contraction principle [1] is one of the most important theorems in fixed point theory. It has applications in many diverse areas.

Definition 1.1 Let M be a nonempty set and f: M → M be a given mapping. We say that x* ∈ M is a fixed point of f if fx* = x*.

Theorem 1.1 (Banach contraction principle [1]). Let (M, d) be a complete metric space and f: M → M be a contractive mapping, i.e., there exists λ ∈ [0, 1) such that for all x, y ∈ M,

$$d\left(fx,fy\right)\le \lambda d\left(x,y\right).$$

(1)

Then the mapping f has a unique fixed point x* ∈ M. Moreover, for every x₀ ∈ M, the sequence (x _k ) defined by: x_k+1= fx _k for all k = 0, 1, 2, ... converges to x*, and the error estimate is given by:

$$d\left(x_k,x^{*}\right)\le \frac{{\lambda }^k}{1-\lambda }d\left(x_0,x_1\right),forallk=0,1,2,\dots$$

Many generalizations of Banach contraction principle exists in the literature. For more details, we refer the reader to [2–4].

To apply the Banach fixed point theorem, the choice of the metric plays a crucial role. In this study, we use the Thompson metric introduced by Thompson [5] for the study of solutions to systems of nonlinear matrix equations involving contractive mappings.

We first review the Thompson metric on the open convex cone P(n) (n ≥ 2), the set of all n×n Hermitian positive definite matrices. We endow P(n) with the Thompson metric defined by:

$$d\left(A,B\right)=max\left\{logM\left(A/B\right),logM\left(B/A\right)\right\},$$

where M(A/B) = inf{λ > 0: A ≤ λB} = λ⁺(B^-1/2AB^-1/2), the maximal eigenvalue of B^-1/2AB^-1/2. Here, X ≤ Y means that Y - X is positive semidefinite and X < Y means that Y - X is positive definite. Thompson [5] (cf. [6, 7]) has proved that P(n) is a complete metric space with respect to the Thompson metric d and d(A, B) = ||log(A^-1/2BA^-1/2)||, where ||·|| stands for the spectral norm. The Thompson metric exists on any open normal convex cones of real Banach spaces [5, 6]; in particular, the open convex cone of positive definite operators of a Hilbert space. It is invariant under the matrix inversion and congruence transformations, that is,

$$d\left(A,B\right)=d\left(A^{-1},B^{-1}\right)=d\left(MA{M}^{*},MB{M}^{*}\right)$$

(2)

for any nonsingular matrix M. The other useful result is the nonpositive curvature property of the Thompson metric, that is,

$$d\left(X^r,Y^r\right)\le rd\left(X,Y\right),r\in \left[0,1\right].$$

(3)

By the invariant properties of the metric, we then have

$$d\left(M{X}^r{M}^{*},M{Y}^r{M}^{*}\right)\le \left|r\right|d\left(X,Y\right),r\in \left[-1,1\right]$$

(4)

for any X, Y ∈ P(n) and nonsingular matrix M.

Lemma 1.1 (see [8]). For all A, B, C, D ∈ P(n), we have

$$d\left(A+B,C+D\right)\le max\left\{d\left(A,C\right),d\left(B,D\right)\right\}.$$

In particular,

$$d\left(A+B,A+C\right)\le d\left(B,C\right).$$

2 Main result

In the last few years, there has been a constantly increasing interest in developing the theory and numerical approaches for HPD (Hermitian positive definite) solutions to different classes of nonlinear matrix equations (see [8–21]). In this study, we consider the following problem: Find (X₁, X₂, ..., X _m ) ∈ (P(n)) ^m solution to the following system of nonlinear matrix equations:

$$X_i^{r_i}=Q_i+\sum _{j=1}^m{\left(A_j^{*}{F}_{ij}\left(X_j\right)A_j\right)}^{{\alpha }_{ij}},i=1,2,\dots ,m,$$

(5)

where r _i ≥ 1, 0 < |α _ij | ≤ 1, Q _i ≥ 0, A _i are nonsingular matrices, and F _ij : P(n) → P (n) are Lipshitzian mappings, that is,

$$\underset{X,Y\in P\left(n\right),X\ne Y}{sup}\frac{d\left(F_{ij}\left(X\right),F_{ij}\left(Y\right)\right)}{d\left(X,Y\right)}=k_{ij}<\infty .$$

(6)

If m = 1 and α₁₁ = 1, then (5) reduces to find X ∈ P(n) solution to X^r = Q + A*F(X)A. Such problem was studied by Liao et al. [15]. Now, we introduce the following definition.

Definition 2.1 We say that Problem (5) is Banach admissible if the following hypothesis is satisfied:

$$\underset{1\le i\le m}{max}\left\{\underset{1\le j\le m}{max}\left\{\left|{\alpha }_{ij}\right|k_{ij}∕r_i\right\}\right\}<1.$$

Our main result is the following.

Theorem 2.1 If Problem (5) is Banach admissible, then it has one and only one solution$\left(X_1^{*},X_2^{*},\dots ,X_m^{*}\right)\in {\left(P\left(n\right)\right)}^m$. Moreover, for any (X₁(0), X₂(0), ..., X _m (0)) ∈ (P(n)) ^m, the sequences (X _i (k))_k≥0, 1 ≤ i ≤ m, defined by:

$$X_i\left(k+1\right)={\left(Q_i+\sum _{j=1}^m{\left(A_j^{*}{F}_{ij}\left(X_j\left(k\right)\right)A_j\right)}^{{\alpha }_{ij}}\right)}^{1∕r_i},$$

(7)

converge respectively to$X_1^{*},X_2^{*},\dots ,X_m^{*}$, and the error estimation is

$$\begin{array}{c}max\left\{d\left(X_1\left(k\right),\underset{1}{\overset{*}{X}}\right),d\left(X_2\left(k\right),X_2^{*}\right),\dots ,d\left(X_m\left(k\right),X_m^{*}\right)\right\}\\ \le \frac{q_m^k}{1-q_m}max\left\{d\left(X_1\left(1\right),X_1\left(0\right)\right),d\left(X_2\left(1\right),X_2\left(0\right)\right),\dots ,d\left(X_m\left(1\right),X_m\left(0\right)\right)\right\},\end{array}$$

(8)

where

$$q_m=\underset{1\le i\le m}{max}\left\{\underset{1\le j\le m}{max}\left\{\left|{\alpha }_{ij}\right|k_{ij}∕r_i\right\}\right\}.$$

Proof. Define the mapping G: (P(n)) ^m → (P(n)) ^m by:

$$G\left(X_1,X_2,\dots ,X_m\right)=\left(G_1\left(X_1,X_2,\dots ,X_m\right),G_2\left(X_1,X_2,\dots ,X_m\right),\dots ,G_m\left(X_1,X_2,\dots ,X_m\right)\right),$$

for all X = (X₁, X₂, ..., X _m ) ∈ (P(n)) ^m , where

$$G_i\left(X\right)={\left(Q_i+\sum _{j=1}^m{\left(A_j^{*}{F}_{ij}\left(X_j\right)A_j\right)}^{{\alpha }_{ij}}\right)}^{1∕r_i},$$

for all i = 1, 2, ..., m. We endow (P(n)) ^m with the metric d _m defined by:

$$d_m\left(\left(X_1,X_2,\dots ,X_m\right),\left(Y_1,Y_2,\dots ,Y_m\right)\right)=max\left\{d\left(X_1,Y_1\right),d\left(X_2,Y_2\right),\dots ,d\left(X_m,Y_m\right)\right\},$$

for all X = (X₁, X₂, ..., X _m ), Y = (Y₁, Y₂, ..., Y _m ) ∈ (P (n)) ^m . Obviously, ((P(n)) ^m , d _m ) is a complete metric space.

We claim that

$$d_m\left(G\left(X\right),G\left(Y\right)\right)\le q_m{d}_m\left(X,Y\right),\mathsf{\text{for all }}X,Y\in {\left(P\left(n\right)\right)}^m.$$

(9)

For all X, Y ∈ (P(n)) ^m , We have

$$d_m\left(G\left(X\right),G\left(Y\right)\right)=\underset{1\le i\le m}{max}\left\{d\left(G_i\left(X\right),G_i\left(Y\right)\right)\right\}.$$

(10)

On the other hand, using the properties of the Thompson metric (see Section 1), for all i = 1, 2, ..., m, we have

$$\begin{array}{l}d(G_i(X),G_i(Y))=d\left({\left(Q_i+{\displaystyle \sum _{j=1}^m{(A_j^{*}{F}_{ij}(X_j)A_j)}^{{\alpha }_{ij}}}\right)}^{1/r_i},{\left(Q_i+{\displaystyle \sum _{j=1}^m{(A_j^{*}{F}_{ij}(Y_j)A_j)}^{{\alpha }_{ij}}}\right)}^{1/r_i}\right)\\ \le \frac{1}{r_i}d\left(Q_i+{\displaystyle \sum _{j=1}^m{(A_j^{*}{F}_{ij}(X_j)A_j)}^{{\alpha }_{ij}}},Q_i+{\displaystyle \sum _{j=1}^m{(A_j^{*}{F}_{ij}(Y_j)A_j)}^{{\alpha }_{ij}}}\right)\\ \le \frac{1}{r_i}d\left({\displaystyle \sum _{j=1}^m{(A_j^{*}{F}_{ij}(X_j)A_j)}^{{\alpha }_{ij}}},{\displaystyle \sum _{j=1}^m{(A_j^{*}{F}_{ij}(Y_j)A_j)}^{{\alpha }_{ij}}}\right)\\ \le \frac{1}{r_i}d\left({(A_1^{*}{F}_{i1}(X_1)A_1)}^{{\alpha }_{i1}}+{\displaystyle \sum _{j=2}^m{(A_j^{*}{F}_{ij}(X_j)A_j)}^{{\alpha }_{ij}}},{(A_1^{*}{F}_{i1}(Y_1)A_1)}^{{\alpha }_{i1}}+{\displaystyle \sum _{j=2}^m{(A_j^{*}{F}_{ij}(Y_j)A_j)}^{{\alpha }_{ij}}}\right)\\ \le \frac{1}{r_i}max\left\{d{((A_1^{*}{F}_{i1}(X_1)A_1)}^{{\alpha }_{i1}},{(A_1^{*}{F}_{i1}(Y_1)A_1)}^{{\alpha }_{i1}}),d\left({\displaystyle \sum _{j=2}^m{(A_j^{*}{F}_{ij}(X_j)A_j)}^{{\alpha }_{ij}}},{\displaystyle \sum _{j=2}^m{(A_j^{*}{F}_{ij}(Y_j)A_j)}^{{\alpha }_{ij}}}\right)\right\}\\ \le \cdot \cdot \cdot \\ \le \frac{1}{r_i}max\left\{d{((A_1^{*}{F}_{i1}(X_1)A_1)}^{{\alpha }_{i1}},{(A_1^{*}{F}_{i1}(Y_1)A_1)}^{{\alpha }_{i1}}),\dots ,d{((A_m^{*}{F}_{im}(X_m)A_m)}^{{\alpha }_{im}},{(A_m^{*}{F}_{im}(Y_m)A_m)}^{{\alpha }_{im}})\right\}\\ \le \frac{1}{r_i}max\left\{\left|{\alpha }_{i1}\right|d(A_1^{*}{F}_{i1}(X_1)A_1,A_1^{*}{F}_{i1}(Y_1)A_1),\dots ,|{\alpha }_{im}|d(A_m^{*}{F}_{im}(X_m)A_m,A_m^{*}{F}_{im}(Y_m)A_m)\right\}\\ \le \frac{1}{r_i}max\left\{\left|{\alpha }_{i1}\right|d(F_{i1}(X_1),F_{i1}(Y_1)),\dots ,|{\alpha }_{im}|d(F_{im}(X_m),F_{im}(Y_m))\right\}\\ \le \frac{1}{r_i}max\left\{\left|{\alpha }_{i1}\right|k_{i1}d(X_1,Y_1),\dots ,|{\alpha }_{im}|k_{im}d(X_m,Y_m)\right\}\\ \le \frac{{\max }_{1\le j\le m}\left\{\right|{\alpha }_{ij}\left|k_{ij}\right\}}{r_i}max\left\{d(X_1,Y_1),\dots ,d(X_m,Y_m)\right\}\\ \le \underset{1\le j\le m}{\max }\left\{\right|{\alpha }_{ij}|k_{ij}/r_i\}{d}_m(X,Y).\end{array}$$

Thus, we proved that for all i = 1, 2, ..., m, we have

$$d\left(G_i\left(X\right),G_i\left(Y\right)\right)\le \underset{1\le j\le m}{max}\left\{\left|{\alpha }_{ij}\right|k_{ij}∕r_i\right\}{d}_m\left(X,Y\right).$$

(11)

Now, (9) holds immediately from (10) and (11). Applying the Banach contraction principle (see Theorem 1.1) to the mapping G, we get the desired result. □

3 Examples and numerical results

3.1 The matrix equation: $\mathbf{X}\mathbf{=}{\left({({({\mathbf{X}}^{\mathbf{1}\mathbf{/}\mathbf{2}}+{\mathbf{B}}_{\mathbf{1}})}^{\mathbf{-}\mathbf{1}/\mathbf{2}}+{\mathbf{B}}_{\mathbf{2}})}^{\mathbf{1}/\mathbf{3}}+{\mathbf{B}}_{\mathbf{3}}\right)}^{\mathbf{1}/\mathbf{2}}$

We consider the problem: Find X ∈ P(n) solution to

$$X={\left({\left({(X^{1/2}+B_1)}^{-1/2}+B_2)\right)}^{1/3}+B_3\right)}^{1/2},$$

(12)

where B _i ≥ 0 for all i = 1, 2, 3.

Problem (12) is equivalent to: Find X₁ ∈ P (n) solution to

$$X_1^{r_1}=Q_1+{\left(A_1^{*}{F}_{11}\left(X_1\right)A_1\right)}^{{\alpha }_{11}},$$

(13)

where r₁ = 2, Q₁ = B₃, A₁ = I _n (the identity matrix), α₁₁ = 1/3 and F₁₁ : P(n) → P (n) is given by:

$$F_{11}\left(X\right)={\left(X^{1∕2}+B_1\right)}^{-1∕2}+B_2.$$

Proposition 3.1 F₁₁is a Lipshitzian mapping with k₁₁ ≤ 1/4.

Proof. Using the properties of the Thompson metric, for all X, Y ∈ P(n), we have

$$\begin{array}{ll}\hfill d\left(F_{11}\left(X\right),F_{11}\left(Y\right)\right)& =d\left({\left(X^{1∕2}+B_1\right)}^{-1∕2}+B_2,{\left(Y^{1∕2}+B_1\right)}^{-1∕2}+B_2\right)\\ \le d\left({\left(X^{1∕2}+B_1\right)}^{-1∕2},{\left(Y^{1∕2}+B_1\right)}^{-1∕2}\right)\\ \le \frac{1}{2}d\left(X^{1∕2}+B_1,Y^{1∕2}+B_1\right)\\ \le \frac{1}{2}d\left(X^{1∕2},Y^{1∕2}\right)\le \frac{1}{4}d\left(X,Y\right).\end{array}$$

Thus, we have k₁₁ ≤ 1/4. □

Proposition 3.2 Problem (13) is Banach admissible.

Proof. We have

$$\frac{\left|{\alpha }_{11}\right|k_{11}}{r_1}\le \frac{\frac{1}{3}\frac{1}{4}}{2}=\frac{1}{24}<1.$$

This implies that Problem (13) is Banach admissible. □

Theorem 3.1 Problem (13) has one and only one solution$X_1^{*}\in P\left(n\right)$. Moreover, for any X₁(0) ∈ P(n), the sequence (X₁(k))_k≥0defined by:

$$X_1\left(k+1\right)={\left({\left({\left(X_1{\left(k\right)}^{1∕2}+B_1\right)}^{-1∕2}+B_2\right)}^{1∕3}+B_3\right)}^{1∕2},$$

(14)

converges to$X_1^{*}$, and the error estimation is

$$d\left(X_1\left(k\right),X_1^{*}\right)\le \frac{q_1^k}{1-q_1}d\left(X_1\left(1\right),X_1\left(0\right)\right),$$

(15)

where q₁ = 1/4.

Proof. Follows from Propositions 3.1, 3.2 and Theorem 2.1. □

Now, we give a numerical example to illustrate our result given by Theorem 3.1.

We consider the 5 × 5 positive matrices B₁, B₂, and B₃ given by:

$$B_1=\left(\begin{array}{ccccc}\hfill 1.0000\hfill & \hfill 0.5000\hfill & \hfill 0.3333\hfill & \hfill 0.2500\hfill & \hfill 0\hfill \\ \hfill 0.5000\hfill & \hfill 1.0000\hfill & \hfill 0.6667\hfill & \hfill 0.5000\hfill & \hfill 0\hfill \\ \hfill 0.3333\hfill & \hfill 0.6667\hfill & \hfill 1.0000\hfill & \hfill 0.7500\hfill & \hfill 0\hfill \\ \hfill 0.2500\hfill & \hfill 0.5000\hfill & \hfill 0.7500\hfill & \hfill 1.0000\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),B_2=\left(\begin{array}{ccccc}\hfill 1.4236\hfill & \hfill 1.3472\hfill & \hfill 1.1875\hfill & \hfill 1.0000\hfill & \hfill 0\hfill \\ \hfill 1.3472\hfill & \hfill 1.9444\hfill & \hfill 1.8750\hfill & \hfill 1.6250\hfill & \hfill 0\hfill \\ \hfill 1.1875\hfill & \hfill 1.8750\hfill & \hfill 2.1181\hfill & \hfill 1.9167\hfill & \hfill 0\hfill \\ \hfill 1.0000\hfill & \hfill 1.6250\hfill & \hfill 1.9167\hfill & \hfill 1.8750\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$$

and

$$B_3=\left(\begin{array}{ccccc}\hfill 2.7431\hfill & \hfill 3.3507\hfill & \hfill 3.3102\hfill & \hfill 2.9201\hfill & \hfill 0\hfill \\ \hfill 3.3507\hfill & \hfill 4.6806\hfill & \hfill 4.8391\hfill & \hfill 4.3403\hfill & \hfill 0\hfill \\ \hfill 3.3102\hfill & \hfill 4.8391\hfill & \hfill 5.2014\hfill & \hfill 4.7396\hfill & \hfill 0\hfill \\ \hfill 2.9201\hfill & \hfill 4.3403\hfill & \hfill 4.7396\hfill & \hfill 4.3750\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$

We use the iterative algorithm (14) to solve (12) for different values of X₁(0):

$$X_1\left(0\right)=M_1=\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 4\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 5\hfill \end{array}\right),X_1\left(0\right)=M_2=\left(\begin{array}{ccccc}\hfill 0.02\hfill & \hfill 0.01\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.01\hfill & \hfill 0.02\hfill & \hfill 0.01\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill & \hfill 0.01\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill & \hfill 0.01\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill \end{array}\right)$$

and

$$X_1\left(0\right)=M_3=\left(\begin{array}{ccccc}\hfill 30\hfill & \hfill 15\hfill & \hfill 10\hfill & \hfill 7.5\hfill & \hfill 6\hfill \\ \hfill 15\hfill & \hfill 30\hfill & \hfill 20\hfill & \hfill 15\hfill & \hfill 12\hfill \\ \hfill 10\hfill & \hfill 20\hfill & \hfill 30\hfill & \hfill 22.5\hfill & \hfill 18\hfill \\ \hfill 7.5\hfill & \hfill 15\hfill & \hfill 22.5\hfill & \hfill 30\hfill & \hfill 24\hfill \\ \hfill 6\hfill & \hfill 12\hfill & \hfill 18\hfill & \hfill 24\hfill & \hfill 30\hfill \end{array}\right).$$

For X₁(0) = M₁, after 9 iterations, we get the unique positive definite solution

$$X_1\left(9\right)=\left(\begin{array}{ccccc}\hfill 1.6819\hfill & \hfill 0.69442\hfill & \hfill 0.61478\hfill & \hfill 0.51591\hfill & \hfill 0\hfill \\ \hfill 0.69442\hfill & \hfill 1.9552\hfill & \hfill 0.96059\hfill & \hfill 0.84385\hfill & \hfill 0\hfill \\ \hfill 0.61478\hfill & \hfill 0.96059\hfill & \hfill 2.0567\hfill & \hfill 0.9785\hfill & \hfill 0\hfill \\ \hfill 0.51591\hfill & \hfill 0.84385\hfill & \hfill 0.9785\hfill & \hfill 1.9227\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$

and its residual error

$$R\left(X_1\left(9\right)\right)=∥X_1\left(9\right)-{\left({\left({\left(X_1{\left(9\right)}^{1∕2}+B_1\right)}^{-1∕2}+B_2\right)}^{1∕3}+B_3\right)}^{1∕2}∥=6.346\times 10^{-13}.$$

For X₁(0) = M₂, after 9 iterations, the residual error

$$R\left(X_1\left(9\right)\right)=1.5884\times 10^{-12}.$$

For X₁(0) = M₃, after 9 iterations, the residual error

$$R\left(X_1\left(9\right)\right)=1.1123\times 10^{-12}.$$

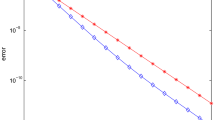
The convergence history of the algorithm for different values of X₁(0) is given by Figure 1, where c₁ corresponds to X₁(0) = M₁, c₂ corresponds to X₁(0) = M₂, and c₃ corresponds to X₁(0) = M₃.

Figure 1

Convergence history for Eq. (12).

3.2 System of three nonlinear matrix equations

We consider the problem: Find (X₁, X₂, X₃) ∈ (P(n))³ solution to

$$\left\{\begin{array}{c}{X}_1=I_n+A_1^{*}{\left(X_1^{1∕3}+B_1\right)}^{1∕2}{A}_1+A_2^{*}{\left(X_2^{1∕4}+B_2\right)}^{1∕3}{A}_2+A_3^{*}{\left(X_3^{1∕5}+B_3\right)}^{1∕4}{A}_3,\\ X_2=I_n+A_1^{*}{\left(X_1^{1∕5}+B_1\right)}^{1∕4}{A}_1+A_2^{*}{\left(X_2^{1∕3}+B_2\right)}^{1∕2}{A}_2+A_3^{*}{\left(X_3^{1∕4}+B_3\right)}^{1∕3}{A}_3,\\ X_3=I_n+A_1^{*}{\left(X_1^{1∕4}+B_1\right)}^{1∕3}{A}_1+A_2^{*}{\left(X_2^{1∕5}+B_2\right)}^{1∕4}{A}_2+A_3^{*}{\left(X_3^{1∕3}+B_3\right)}^{1∕2}{A}_3,\end{array}\right.$$

(16)

where A _i are n × n singular matrices.

Problem (16) is equivalent to: Find (X₁, X₂, X₃) ∈ (P(n))³ solution to

$$X_i^{r_i}=Q_i+\sum _{j=1}^3{\left(A_j^{*}{F}_{ij}\left(X_j\right)A_j\right)}^{{\alpha }_{ij}},i=1,2,3,$$

(17)

where r₁ = r₂ = r₃ = 1, Q₁ = Q₂ = Q₃ = I _n and for all i, j ∈ {1, 2, 3}, α _ij = 1,

$$F_{ij}\left(X_j\right)={\left(X_j^{{\theta }_{ij}}+B_j\right)}^{{\gamma }_{ij}},\theta =\left({\theta }_{ij}\right)=\left(\begin{array}{ccc}\hfill 1∕3\hfill & \hfill 1∕4\hfill & \hfill 1∕5\hfill \\ \hfill 1∕5\hfill & \hfill 1∕3\hfill & \hfill 1∕4\hfill \\ \hfill 1∕4\hfill & \hfill 1∕5\hfill & \hfill 1∕3\hfill \end{array}\right),\gamma =\left({\gamma }_{ij}\right)=\left(\begin{array}{ccc}\hfill 1∕2\hfill & \hfill 1∕3\hfill & \hfill 1∕4\hfill \\ \hfill 1∕4\hfill & \hfill 1∕2\hfill & \hfill 1∕3\hfill \\ \hfill 1∕3\hfill & \hfill 1∕4\hfill & \hfill 1∕2\hfill \end{array}\right).$$

Proposition 3.3 For all i, j ∈ {1, 2, 3}, F _ij : P(n) → P(n) is a Lipshitzian mapping with k _ij ≤ γ _ij θ _ij .

Proof. For all X, Y ∈ P(n), since θ _ij , γ _ij ∈ (0, 1), we have

$$\begin{array}{ll}\hfill d\left(F_{ij}\left(X\right),F_{ij}\left(Y\right)\right)& =d\left({\left(X^{{\theta }_{ij}}+B_j\right)}^{{\gamma }_{ij}},{\left(Y^{{\theta }_{ij}}+B_j\right)}^{{\gamma }_{ij}}\right)\\ \le {\gamma }_{ij}d\left(X^{{\theta }_{ij}}+B_j,Y^{{\theta }_{ij}}+B_j\right)\\ \le {\gamma }_{ij}d\left(X^{{\theta }_{ij}},Y^{{\theta }_{ij}}\right)\\ \le {\gamma }_{ij}{\theta }_{ij}d\left(X,Y\right).\end{array}$$

Then, F _ij is a Lipshitzian mapping with k _ij ≤ γ _ij θ _ij . □

Proposition 3.4 Problem (17) is Banach admissible.

Proof. We have

$$\begin{array}{ll}\hfill \underset{1\le i\le 3}{max}\left\{\underset{1\le j\le 3}{max}\left\{\left|{\alpha }_{ij}\right|k_{ij}∕r_i\right\}\right\}& =\underset{1\le i,j\le 3}{max}{k}_{ij}\\ \le \underset{1\le i,j\le 3}{max}{\gamma }_{ij}{\theta }_{ij}\\ =1∕6<1.\end{array}$$

This implies that Problem (17) is Banach admissible. □

Theorem 3.2 Problem (16) has one and only one solution$\left(X_1^{*},X_2^{*},X_3^{*}\right)\in {\left(P\left(n\right)\right)}^3$. Moreover, for any (X₁(0), X₂(0), X₃(0)) ∈ (P(n))³, the sequences (X _i (k))_k≥0, 1 ≤ i ≤ 3, defined by:

$$X_i\left(k+1\right)=I_n+\sum _{j=1}^3{A}_j^{*}{F}_{ij}\left(X_j\left(k\right)\right)A_j,$$

(18)

converge respectively to$X_1^{*},X_2^{*},X_3^{*}$, and the error estimation is

$$\begin{array}{c}max\left\{d\left(X_1\left(k\right),\underset{1}{\overset{*}{X}}\right),d\left(X_2\left(k\right),X_2^{*}\right),d\left(X_3\left(k\right),X_3^{*}\right)\right\}\\ \le \frac{q_3^k}{1-q_3}max\left\{d\left(X_1\left(1\right),X_1\left(0\right)\right),d\left(X_2\left(1\right),X_2\left(0\right)\right),d\left(X_3\left(1\right),X_3\left(0\right)\right)\right\},\end{array}$$

(19)

where q₃ = 1/6.

Proof. Follows from Propositions 3.3, 3.4 and Theorem 2.1. □

Now, we give a numerical example to illustrate our obtained result given by Theorem 3.2.

We consider the 3 × 3 positive matrices B₁, B₂ and B₃ given by:

$$B_1=\left(\begin{array}{ccc}\hfill 1.\hfill & \hfill 0.5\hfill & \hfill 0\hfill \\ \hfill 0.5\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),B_2=\left(\begin{array}{ccc}\hfill 1.25\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 1.25\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\mathsf{\text{and}}{B}_3=\left(\begin{array}{ccc}\hfill 1.75\hfill & \hfill 1.625\hfill & \hfill 0\hfill \\ \hfill 1.625\hfill & \hfill 1.75\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).$$

We consider the 3 × 3 nonsingular matrices A₁, A₂ and A₃ given by:

$$A_1=\left(\begin{array}{ccc}\hfill 0.3107\hfill & \hfill -0.5972\hfill & \hfill 0.7395\hfill \\ \hfill 0.9505\hfill & \hfill 0.1952\hfill & \hfill -0.2417\hfill \\ \hfill 0\hfill & \hfill -0.7780\hfill & \hfill -0.6282\hfill \end{array}\right),A_2=\left(\begin{array}{ccc}\hfill 1.5\hfill & \hfill -2\hfill & \hfill 0.5\hfill \\ \hfill 0.5\hfill & \hfill 0\hfill & \hfill -0.5\hfill \\ \hfill -0.5\hfill & \hfill 2\hfill & \hfill -1.5\hfill \end{array}\right)$$

and

$$A_3=\left(\begin{array}{ccc}\hfill -1\hfill & \hfill -1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill -1\hfill & \hfill 1\hfill \\ \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill \end{array}\right).$$

We use the iterative algorithm (18) to solve Problem (16) for different values of (X₁(0), X₂(0), X₃(0)):

$$X_1\left(0\right)=X_2\left(0\right)=X_3\left(0\right)=M_1=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 3\hfill \end{array}\right),$$

$$X_1\left(0\right)=X_2\left(0\right)=X_3\left(0\right)=M_2=\left(\begin{array}{ccc}\hfill 0.02\hfill & \hfill 0.01\hfill & \hfill 0\hfill \\ \hfill 0.01\hfill & \hfill 0.02\hfill & \hfill 0.01\hfill \\ \hfill 0\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill \end{array}\right)$$

and

$$X_1\left(0\right)=X_2\left(0\right)=X_3\left(0\right)=M_3=\left(\begin{array}{ccc}\hfill 30\hfill & \hfill 15\hfill & \hfill 10\hfill \\ \hfill 15\hfill & \hfill 30\hfill & \hfill 20\hfill \\ \hfill 10\hfill & \hfill 20\hfill & \hfill 30\hfill \end{array}\right).$$

The error at the iteration k is given by:

$$R\left(X_1\left(k\right),X_2\left(k\right),X_3\left(k\right)\right)=\underset{1\le i\le 3}{max}∥X_i\left(k\right)-I_3-\sum _{j=1}^3{A}_j^{*}{F}_{ij}\left(X_j\left(k\right)\right)A_j∥.$$

For X₁(0) = X₂(0) = X₃(0) = M₁, after 15 iterations, we obtain

$$X_1\left(15\right)=\left(\begin{array}{ccc}\hfill 10.565\hfill & \hfill -4.4081\hfill & \hfill 2.7937\hfill \\ \hfill -4.4081\hfill & \hfill 16.883\hfill & \hfill -6.6118\hfill \\ \hfill 2.7937\hfill & \hfill -6.6118\hfill & \hfill 9.7152\hfill \end{array}\right),X_2\left(15\right)=\left(\begin{array}{ccc}\hfill 11.512\hfill & \hfill -5.8429\hfill & \hfill 3.1922\hfill \\ \hfill -5.8429\hfill & \hfill 19.485\hfill & \hfill -7.9308\hfill \\ \hfill 3.1922\hfill & \hfill -7.9308\hfill & \hfill 10.68\hfill \end{array}\right)$$

and

$$X_3\left(15\right)=\left(\begin{array}{ccc}\hfill 11.235\hfill & \hfill -3.5241\hfill & \hfill 3.2712\hfill \\ \hfill -3.5241\hfill & \hfill 17.839\hfill & \hfill -7.8035\hfill \\ \hfill 3.2712\hfill & \hfill -7.8035\hfill & \hfill 11.618\hfill \end{array}\right).$$

The residual error is given by:

$$R\left(X_1\left(15\right),X_2\left(15\right),X_3\left(15\right)\right)=4.722\times 10^{-15}.$$

For X₁(0) = X₂(0) = X₃(0) = M₂, after 15 iterations, the residual error is given by:

$$R\left(X_1\left(15\right),X_2\left(15\right),X_3\left(15\right)\right)=4.911\times 10^{-15}.$$

For X₁(0) = X₂(0) = X₃(0) = M₃, after 15 iterations, the residual error is given by:

$$R\left(X_1\left(15\right),X_2\left(15\right),X_3\left(15\right)\right)=8.869\times 10^{-15}.$$

The convergence history of the algorithm for different values of X₁(0), X₂(0), and X₃(0) is given by Figure 2, where c₁ corresponds to X₁(0) = X₂(0) = X₃(0) = M₁, c₂ corresponds to X₁(0) = X₂(0) = X₃(0) = M₂ and c₃ corresponds to X₁(0) = X₂(0) = X₃(0) = M₃.

Figure 2

Convergence history for Sys. (16).