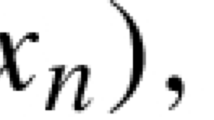On rate of convergence of various iterative schemes

Abstract

In this note, by taking an counter example, we prove that the iteration process due to Agarwal et al. (J. Nonlinear Convex. Anal. 8 (1), 61-79, 2007) is faster than the Mann and Ishikawa iteration processes for Zamfirescu operators.

1 Introduction

For a nonempty convex subset C of a normed space E and T : C → C, (a) the Mann iteration process [1] is defined by the following sequence{x _n }:

$$\left\{\begin{array}{c}\hfill x_0\in C,\hfill \\ \hfill x_{n+1}=\left(1-b_n\right)x_n+b_{n}T{x}_n,n\ge 0,\hfill \end{array}\right.\left(M_n,\right)$$

where {b _n } is a sequence in [0, 1].

• (b) the sequence {x _n } defined by

  $$\left\{\begin{array}{c}\hfill x_0\in C,\hfill \\ \hfill y_n=\left(1-{b^{\prime }}_n\right)x_n+{b^{\prime }}_{n}T{x}_n,\hfill \\ \hfill x_{n+1}=\left(1-b_n\right)x_n+b_{n}T{y}_n,n\ge 0,\hfill \end{array}\right.\left(I_n,\right)$$

where {b _n }, $\left\{b_n^{\prime }\right\}$ are sequences in [0, 1] is known as the Ishikawa [2] iteration process.

• (c) the sequence {x _n } defined by

  $$\left\{\begin{array}{c}\hfill x_0\in C,\hfill \\ \hfill y_n=\left(1-{b^{\prime }}_n\right)x_n+{b^{\prime }}_{n}T{x}_n,\hfill \\ \hfill x_{n+1}=\left(1-b_n\right)T{x}_n+b_{n}T{y}_n,n\ge 0,\hfill \end{array}\right.\left(AR{S}_n,\right)$$

where {b _n }, $\left\{b_n^{\prime }\right\}$ are sequences in [0, 1] is known as the Agarwal et al. [3] iteration process.

Definition 1. [4] Suppose that {a _n } and {b _n } are two real convergent sequences with limits a and b, respectively. Then, {a _n } is said to converge faster than {b _n } if

$$\underset{n\to \infty }{lim}\left|\frac{a_n-a}{b_n-b}\right|=0.$$

Theorem 2. [5] Let (X, d) be a complete metric space, and T : X → X a mapping for which there exist real numbers, a, b, and c satisfying 0 < a < 1, 0 < b, $c<\frac{1}{2}$ such that for each pair x, y ∈ X, at least one of the following is true:

(z 1) d(Tx, Ty) ≤ ad(x, y),

(z 2) d(Tx, Ty) ≤ b [d(x, Tx) + d(y, Ty)],

(z 3) d(Tx, Ty) ≤ c [d(x, Ty) + d(y, Tx)].

Then, T has a unique fixed point p and the Picard iteration ${\left\{x_n\right\}}_{n=1}^{\infty }$ defined by

$$x_{n+1}=T{x}_n,n=0,1,2,\dots ,$$

converges to p, for any x₀ ∈ X.

Remark 3. An operator T that satisfies the contraction conditions (z 1) - (z 3) of Theorem 2 will be called a Zamfirescu operator [[4, 6, 7]] and is denoted by Z.

In [6, 7], Berinde introduced a new class of operators on a normed space E satisfying

$$\left|\right|Tx-Ty\left|\right|\le \delta \left|\right|x-y\left|\right|+L\left|\right|Tx-x\left|\right|\left(B\right)$$

for any x, y ∈ E, 0 ≤ δ < 1 and L ≥ 0. He proved that this class is wider than the class of Zamfiresu operators.

The following results are proved in [6, 7].

Theorem 4. [7] Let C be a nonempty closed convex subset of a normed space E. Let T : C → C be an operator satisfying (B). Let {x _n } be defined through the iterative process (M _n ). If F (T) ≠ Ø and $\sum b_n=\infty$, then {x _n } converges strongly to the unique fixed point of T.

Theorem 5. [6] Let C be a nonempty closed convex subset of an arbitrary Banach space E and T : C → C be an operator satisfying (B). Let {x _n } be defined through the iterative process I _n and x₀ ∈ C, where {b _n } and $\left\{b_n^{\prime }\right\}$ are sequences of positive numbers in [0, 1] with {b _n } satisfying $\sum b_n=\infty$. Then {x _n } converges strongly to the fixed point of T.

The following theorem was presented in [8].

Theorem 6. Let C be a closed convex subset of an arbitrary Banach space E. Let the Mann and Ishikawa iteration processes denoted by M _n and I _n , respectively, with {b _n } and $\left\{b_n^{\prime }\right\}$ be real sequences satisfying (i) 0 ≤ b _n , $b_n^{\prime }\le 1$, and (ii) $\sum b_n=\infty$. Then, M _n and I _n converge strongly to the unique fixed point of a Zamfirescu operator T : C → C, and moreover, the Mann iteration process converges faster than the Ishikawa iteration process to the fixed point of T.

Remark 7. In [9], Qing and Rhoades, by taking a counter example, showed that the Ishikawa iteration process is faster than the Mann iteration process for Zamfirescu operators. Thus, Theorem in [8] and the presentation in [9] contradict to each other (see also [10]).

In this note, we establish a general theorem to approximate fixed points of quasi-contractive

operators in a Banach space through the iteration process ARS _n , due to Agarwal et al. [3]. Our result generalizes and improves upon, among others, the corresponding results of Babu and Prasad [8] and Berinde [4, 6, 7].

We also prove that the iteration process ARS _n is faster than the Mann iteration process M _n and the Ishikawa iteration process I _n for Zamfirescu operators.

2 Main results

We now prove our main results.

Theorem 8. Let C be a nonempty closed convex subset of an arbitrary Banach space E and T : C → C be an operator satisfying (B). Let {x _n } be defined through the iterative process ARS _n and x₀ ∈ C, where {b _n }, $\left\{b_n^{\prime }\right\}$ are sequences in [0, 1] satisfying $\sum b_n=\infty$. Then, {x _n } converges strongly to the fixed point of T.

Proof. Assume that F(T) ≠ Ø and w ∈ F(T), then using (ARS _n ), we have

$$\begin{array}{lll}\hfill \left|\right|x_{n+1}-w\left|\right|& =\left|\right|\left(1-b_n\right)T{x}_n+b_{n}T{y}_n-w\left|\right|& \hfill \text{(1)}\\ =\left|\right|\left(1-b_n\right)\left(T{x}_n-w\right)+b_n\left(T{y}_n-w\right)\left|\right|& \hfill \text{(2)}\\ \le \left(1-b_n\right)\left|\right|T{x}_n-w\left|\right|+b_n\left|\right|T{y}_n-w\left|\right|.& \hfill \text{(3)}\\ \hfill \text{(4)}\end{array}$$

(2.1)

Now using (B) with x = w, y = x _n , and then with x = w, y = y _n , we obtain the following two inequalities,

$$\left|\right|T{x}_n-w\left|\right|\le \delta \left|\right|x_n-w\left|\right|,$$

(2.2)

and

$$\left|\right|T{y}_n-w\left|\right|\le \delta \left|\right|y_n-w\left|\right|.$$

(2.3)

By substituting (2.2) and (2.3) in (2.1), we obtain

$$\left|\right|x_{n+1}-w\left|\right|\le \left(1-b_n\right)\delta \left|\right|x_n-w\left|\right|+b_n\delta \left|\right|y_n-w\left|\right|.$$

(2.4)

In a similar fashion, again by using (ARS _n ), we can get

$$\left|\right|y_n-w\left|\right|\le \left(1-\left(1-\delta \right)b_n^{\prime }\right)\left|\right|x_n-w\left|\right|.$$

(2.5)

From (2.4) and (2.5), we have

$$\left|\right|x_{n+1}-w\left|\right|\le \left[1-\left(1-\delta \right)b_n\left(1+\delta b_n^{\prime }\right)\right]\left|\right|x_n-w\left|\right|.$$

(2.6)

It may be noted that for δ ∈ [0, 1) and {η _n } ∈ [0, 1], the following inequality holds:

$$1\le 1+\delta {\eta }_n\le 1+\delta .$$

(2.7)

From (2.6) and (2.7), we get

$$\left|\right|x_{n+1}-w\left|\right|\le \left(1-\left(1-\delta \right)b_n\right)\left|\right|x_n-w\left|\right|.$$

(2.8)

By (2.8) we inductively obtain

$$\left|\right|x_{n+1}-w\left|\right|\le \prod _{k=0}^n\left[1-\delta \left(1-\delta \right)b_k\right]\left|\right|x_0-w\left|\right|,n=0,1,2,\dots$$

(2.9)

Using the fact that 0 ≤ δ < 1, 0 ≤ b _n ≤ 1, and $\sum b_n=\infty$, it results that

$$\underset{n\to \infty }{lim}\prod _{k=0}^n\left[1-\delta \left(1-\delta \right)b_k\right]=0,$$

which by (2.9) implies

$$\underset{n\to \infty }{lim}\left|\right|x_{n+1}-w\left|\right|=0.$$

Consequently x _n → w ∈ F and this completes the proof. □

Now by an counter example, we prove that the iteration process ARS _n due to Agarwal et al. [3] is faster than the Mann and Ishikawa iteration processes for Zamfirescu operators.

Example 9. [9] Suppose $T:\left[0,1\right]\to \left[0,1\right]:=\frac{1}{2}x$, $b_n=0=b_n^{\prime }$, n = 1, 2,..., 15. $b_n=\frac{4}{\sqrt{n}}=b_n^{\prime }$, n ≥ 16.

It is clear that T is a Zamfirescu operator with a unique fixed point 0. Also, it is easy to see that Example 9 satisfies all the conditions of Theorem 8.

Proof. Since $b_n=0=b_n^{\prime }$, n = 1, 2,..., 15, so M _n = x₀ = I _n = ARS _n , n = 1, 2,..., 16. Suppose x₀ ≠ 0. For M _n , I _n and ARS _n iteration processes, we have

$$\begin{array}{lll}\hfill M_n& =\left(1-b_n\right)x_n+b_{n}T{x}_n& \hfill \text{(1)}\\ =\left(1-\frac{4}{\sqrt{n}}\right)x_n+\frac{4}{\sqrt{n}}\frac{1}{2}{x}_n& \hfill \text{(2)}\\ =\left(1-\frac{2}{\sqrt{n}}\right)x_n& \hfill \text{(3)}\\ =\cdot \cdot \cdot & \hfill \text{(4)}\\ =\prod _{i=16}^n\left(1-\frac{2}{\sqrt{i}}\right)x_0,& \hfill \text{(5)}\\ \hfill \text{(6)}\end{array}$$

$$\begin{array}{lll}\hfill I_n& =\left(1-b_n\right)x_n+b_{n}T\left(\left(1-{b^{\prime }}_n\right)x_n+{b^{\prime }}_{n}T{x}_n\right)& \hfill \text{(1)}\\ =\left(1-\frac{4}{\sqrt{n}}\right)x_n+\frac{4}{\sqrt{n}}\frac{1}{2}\left(1-\frac{2}{\sqrt{n}}\right)x_n& \hfill \text{(2)}\\ =\left(1-\frac{2}{\sqrt{n}}-\frac{4}{n}\right)x_n& \hfill \text{(3)}\\ =\cdot \cdot \cdot & \hfill \text{(4)}\\ =\prod _{i=16}^n\left(1-\frac{2}{\sqrt{i}}-\frac{4}{i}\right)x_0,& \hfill \text{(5)}\\ \hfill \text{(6)}\end{array}$$

and

$$\begin{array}{lll}\hfill AR{S}_n& =\left(1-b_n\right)T{x}_n+b_{n}T\left(\left(1-{b^{\prime }}_n\right)x_n+{b^{\prime }}_{n}T{x}_n\right)& \hfill \text{(1)}\\ =\left(1-\frac{4}{\sqrt{n}}\right)\frac{x_n}{2}+\frac{4}{\sqrt{n}}\frac{1}{2}\left(1-\frac{2}{\sqrt{n}}\right)x_n& \hfill \text{(2)}\\ =\left(\frac{1}{2}-\frac{4}{n}\right)x_n& \hfill \text{(3)}\\ =\cdot \cdot \cdot & \hfill \text{(4)}\\ =\prod _{i=16}^n\left(\frac{1}{2}-\frac{4}{i}\right)x_0.& \hfill \text{(5)}\\ \hfill \text{(6)}\end{array}$$

Now consider

$$\begin{array}{lll}\hfill \left|\frac{AR{S}_n-0}{M_n-0}\right|& =\left|\frac{\prod _{i=16}^n\left(\frac{1}{2}-\frac{4}{i}\right)x_0}{\prod _{i=16}^n\left(1-\frac{2}{\sqrt{i}}\right)x_0}\right|& \hfill \text{(1)}\\ =\left|\frac{\prod _{i=16}^n\left(\frac{1}{2}-\frac{4}{i}\right)}{\prod _{i=16}^n\left(1-\frac{2}{\sqrt{i}}\right)}\right|& \hfill \text{(2)}\\ =\left|\prod _{i=16}^n\left(1-\frac{\frac{1}{2}-\frac{2}{\sqrt{i}}+\frac{4}{i}}{\left(1-\frac{2}{\sqrt{i}}\right)}\right)\right|& \hfill \text{(3)}\\ =\left|\prod _{i=16}^n\left(1-\frac{1}{2\sqrt{i}}\frac{i-4\sqrt{i}+8}{\sqrt{i}-2}\right)\right|.& \hfill \text{(4)}\\ \hfill \text{(5)}\end{array}$$

It is easy to see that

$$\begin{array}{lll}\hfill 0& \le \underset{n\to \infty }{lim}\prod _{i=16}^n\left(1-\frac{1}{2\sqrt{i}}\frac{i-4\sqrt{i}+8}{\sqrt{i}-2}\right)& \hfill \text{(1)}\\ \le \underset{n\to \infty }{lim}\prod _{i=16}^n\left(1-\frac{1}{i}\right)& \hfill \text{(2)}\\ =\underset{n\to \infty }{lim}\frac{15}{n}& \hfill \text{(3)}\\ =0.& \hfill \text{(4)}\\ \hfill \text{(5)}\end{array}$$

Hence

$$\underset{n\to \infty }{lim}\left|\frac{AR{S}_n-0}{M_n-0}\right|=0.$$

Thus, the iteration process due to Agarwal et al. [3] converges faster than the Mann iteration process to the fixed point 0 of T.

Similarly

$$\begin{array}{lll}\hfill \left|\frac{AR{S}_n-0}{I_n-0}\right|& =\left|\frac{\prod _{i=16}^n\left(\frac{1}{2}-\frac{4}{i}\right)x_0}{\prod _{i=16}^n\left(1-\frac{2}{\sqrt{i}}-\frac{4}{i}\right)x_0}\right|& \hfill \text{(1)}\\ =\left|\frac{\prod _{i=16}^n\left(\frac{1}{2}-\frac{4}{i}\right)}{\prod _{i=16}^n\left(1-\frac{2}{\sqrt{i}}-\frac{4}{i}\right)}\right|& \hfill \text{(2)}\\ =\left|\prod _{i=16}^n\left(1-\frac{\frac{1}{2}-\frac{2}{\sqrt{i}}}{\left(1-\frac{2}{\sqrt{i}}-\frac{4}{i}\right)}\right)\right|& \hfill \text{(3)}\\ =\left|\prod _{i=16}^n\left(1-\frac{\sqrt{i}}{2}\frac{i-4}{i-2\sqrt{i}-4}\right)\right|,& \hfill \text{(4)}\\ \hfill \text{(5)}\end{array}$$

with

$$\begin{array}{lll}\hfill 0& \le \underset{n\to \infty }{lim}\prod _{i=16}^n\left(1-\frac{\sqrt{i}}{2}\frac{\sqrt{i}-4}{i-2\sqrt{i}-4}\right)& \hfill \text{(1)}\\ \le \underset{n\to \infty }{lim}\prod _{i=16}^n\left(1-\frac{1}{i}\right)& \hfill \text{(2)}\\ =\underset{n\to \infty }{lim}\frac{15}{n}& \hfill \text{(3)}\\ =0,& \hfill \text{(4)}\\ \hfill \text{(5)}\end{array}$$

implies

$$\underset{n\to \infty }{lim}\left|\frac{AR{S}_n-0}{I_n-0}\right|=0.$$

Thus, the iteration process due to Agarwal et al. [3] converges faster than the Ishikawa iteration process to the fixed point 0 of T. □