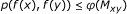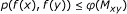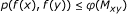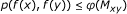1. Introduction and Preliminary

Recently, Nieto and Rodriguez-Lopez [1, 2], Ran and Reurins [3], Petrusel and Rus [4] presented some new results in partially ordered metric spaces. Their main idea was to combine the ideas of iterative technique in the contractive mapping with these in monotone technique.

Recently, Kada et al. [5, 6] in 1996 introduced the concept of w-distance in a metric space and prove some fixed point theorems. For the study of fixed point theorem concerning generalized distance followed in other articles, see [5, 7–15].

The aim of this article is to use the concept of w-distance to generalize the fixed point theorems in partially ordered metric spaces. Our results not only generalize some fixed point theorems, but also improve and simplify the previous results.

In the sequel, we state some definitions and a lemma which we will use in our main results.

Definition 1.1. ([5, 8, 10]) Let (X, d) be a metric space. Then, a function p : X × X → [0, ∞) is called a w-distance on X if the following conditions are satisfied:

  1. (a)

    p(x, z) ≤ p(x, y) + p(y, z) for any x, y, z ∈ X;

  2. (b)

    for any x ∈ X, p(x, .) : X → [0, ∞) is lower semi-continuous;

  3. (c)

    for any ε > 0, there exists δ > 0 such that p(x, z) ≤ δ and p(z, y) ≤ δ imply d(x, y) ≤ ε.

We know that a real-valued function f defined in a metric space X is said to be lower semi-continuous at a point x0 ∈ X if either or , whenever x n ∈ X for each n ∈ N and x n → x0.

Lemma 1.2. ([5, 7]) Let (X, d) be a metric space and p be a w-distance on X. Let {x n }, {y n } be sequences in X, {α n }, {β n } be sequences in [0, ∞) converging to zero and let x, y, z ∈ X. Then, the following conditions hold:

  1. (1)

    If p(x n , y) ≤ α n and p(x n , z) ≤ β n for any n ∈ N, then y = z. In particular, if p(x.y) = 0 and p(x, z) = 0, then y = z;

  2. (2)

    If p(x n , y n ) ≤ α n and p(x n , z) ≤ β n for any n ∈ N, then d(y n , z) → 0;

  3. (3)

    If p(x n , x m ) ≤ α n for any n, m ∈ N with m > n, then {x n } is a Cauchy sequence;

  4. (4)

    If p(y, x n ) ≤ α n for any n ∈ N, then {x n } is a Cauchy sequence.

Let f : X → X be an operator:

  1. (1)

    I(f) is the set of all nonempty invariant subsets of f, i.e., I(f) = {Y ⊂ X : f(Y ) ⊂ Y } and F f = {x ∈ X : x = f(x)}.

  2. (2)

    The operator f is called Picard operator (briefly, PO) if there exists x* ∈ X such that F f = {x*} and, for all x ∈ X, {fn (x)} converges to x*.

  3. (3)

    The operator f is called orbitally U-continuous for any U ⊂ X × X if the following condition holds:

For any x ∈ X, as i → ∞ and for any i ∈ N imply that as i → ∞.

  1. (4)

    Let (X, ≤) be a partially ordered set. Then,

and [x, y]≤ = {z ∈ X : x ≤ z ≤ y}, where x, y ∈ X and x ≤ y.

  1. (5)

    If g : Y → Y is an operator, then the Cartesian product of f and g is the mapping f × g : X × Y → X × Y defined by (f × g)(x, y) = (f(x), g(y)) for all (x, y) ∈ X × Y.

  2. (6)

    φ : R + → R + is said to be a comparison function if it is increasing and φn (t) → 0 as n → ∞. As a consequence, we also have φ (t) < t for any t > 0, φ (0) = 0, and φ is right continuous at 0.

2. Main Results

Now, we give the main results of this article.

Theorem 2.1. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator. Let p be a w-distance on (X, d) and suppose that

  1. (a)

    X ≤ ∈ I(f × f );

  2. (b)

    there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;

  3. (c)

    (c 1) f is orbitally continuous or

(c2) f is orbitally X≤-continuous and there exists a subsequenceof {f n (x0)} such thatfor any k ∈ N ;

  1. (d)

    there exists a comparison function φ : R + → R + such that

for all (x, y) ∈ X≤, where

  1. (e)

    the metric d is complete.

Then F f ≠ ∅.

Proof. If f(x0) = x0, then the proof is completed. Let x0 ∈ X be such that (x0, f (x0)) ∈ X≤. By (a), since (f × f )(X≤) ⊂ X≤, we have (f × f )(x0, f (x o )) ∈ X≤ and so (f(x0), f2(x o )) ∈ X≤.

Continuing this process, we obtain

for any n ∈ N.

Now, we show that

(3.1)

for any n ∈ N. Let p0 = p(x0, f (x0)) and p n = p(f n (x0), fn+1(x0)) for any n ∈ N. Then we have

(3.2)

for any n ∈ N. If max{pn-1, p n } = pn-1, then (3.1) follows. Otherwise, max{pn-1, p n } = p n Then, by (3.2), we have p n ≤ φ(p n ) ≤ p n and so p n = 0 and (3.1) follows. By induction, we obtain

or, equivalently,

for any n ∈ N, Now, we have

as n → ∞.

Similarly, we have

as n → ∞ and so, by induction, we obtain

(3.3)

as n → ∞ for any k > 0. Therefore, {fn (x0)} is a Cauchy sequence in X. Since X is complete, there exists x* ∈ X such that fn (x0) → x* as n → ∞.

Now, we show that x* is a fixed point. If (c1) holds, then fn+1(x0) → f (x*) and, by lower semi-continuity of p(fn (x0), ·), we have

and α n , β n → 0 as n → ∞. Thus, by (3.3) and Lemma 1.2, we conclude that f (x*) = x*.

Now, suppose that (c2) holds. Since converges to x* and f is X≤-orbitally continuous, it follows that converges to f (x*). Similarly, by lower semi-continuity of p(fn (x0), ·), we conclude that f (x*) = x*. This completes the proof. □

Corollary 2.2. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.

Let p be a w-distance on (X, d) and suppose that

  1. (a)

    X ≤ ∈ I(f × f );

  2. (b)

    there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;

  3. (c)

    (c 1)) f is orbitally continuous or

(c2) f is orbitally X≤-continuous and there exists a subsequenceof {fn (x0)} such thatfor any k ∈ N ;

  1. (d)

    and there is a comparison function φ : R + → R + such that

for any (x, y) ∈ X≤, where

  1. (e)

    the metric d is complete;

  2. (f)

    if (x, y) ∈ X ≤ and (y, z) ∈ X ≤ .vskip 1 mm

Then, F f ≠ ∅.

Theorem 2.3. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.

Let p be a w-distance on (X, d) and suppose that

  1. (a)

    X ≤ ∈ I(f × f );

  2. (b)

    There exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;

  3. (c)

    (c 1) f is orbitally continuous or

(c2) f is orbitally X≤-continuous and there exists a subsequenceof {fn(x0)} such thatfor any k ∈ N ;

  1. (d)

    there is a comparison function φ : R + → R + such that

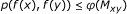
for any (x, y) ∈ X≤, where

  1. (e)

    the metric d is complete;

  2. (f)

    if x, y ∈ X with (x, y) ∉ X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ . .

Then, f is PO.

Proof. According to Theorem 2.1, there exists x* ∈ X such that f(x*) = x*. Take x ∈ X.

If (x, x0) ∈ X≤, then (f n (x), f n (x 0)) ∈ X≤ and so

for any n ∈ N. Thus, by Lemma 1.2, fn (x) → x* as n → ∞.

If (x, x0) ∉ X≤, then there exists z ∈ X such that (x, z) ∈ X≤ and (x0, z) ∈ X≤ and so

for any n ∈ N. Thus, by Lemma 1.2, we have fn (z) → x* as n → ∞. Also, since (x, z) ∈ X≤, we have f n (z) → x* as n → ∞. Consequently, f n (x) → x* as n → ∞.

Now, if there exist y ∈ X such that f(y) = y, then

and so, by Lemma 2.1, y = x*, i.e., F f = {x*}. This completes the proof. □

Corollary 2.4. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.

Let p be a w-distance on (X, d) and suppose that

  1. (a)

    if x, y ∈ X with (x, y)X ≤ there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;

  2. (b)

    X ≤ ∈ I(f × f ) ;

  3. (c)

    There exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;

  4. (d)

    (d 1) f is orbitally continuous or

(d2) f is orbitally X≤-continuous and there exists a subsequenceof {fn (x0)} such thatfor any k ∈ N ;

  1. (e)

    there is a comparison function φ : R + → R + such that

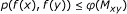
for any (x, y) ∈ X≤, where

  1. (f)

    the metric d is complete,

Then, f is PO.

Corollary 2.5. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.

Let p be a w-distance on (X, d) and suppose that

  1. (a)

    if x, y ∈ X with (x, y)X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;

  2. (b)

    if (x, y) ∈ X ≤ and (y, z) ∈ X ≤, then (x, z) ∈ X ≤ ;

  3. (c)

    f is orbitally continuous (iv) there is a comparison function φ : R + → R + such that

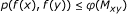
for any (x, y) ∈ X≤, where

  1. (d)

    the metric d is complete,

Then, f is PO.

Corollary 2.6. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.

Let p be a w-distance on (X, d) and suppose that

  1. (a)

    if x, y ∈ X with (x, y)X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;

  2. (b)

    X ≤ ∈I(f × f ) ;

  3. (c)

    there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;

  4. (d)

    if (x, y) ∈ X ≤ and (y, z) ∈ X ≤, then (x, z) ∈ X ≤ ;

  5. (e)

    (e 1) f is orbitally continuous or

(e2) f is orbitally X≤-continuous and there exists a subsequenceof {fn (x0)} such thatfor any k ∈ N ;

  1. (f)

    there is a comparison function φ : R + → R + such that

for any (x, y) ∈ X≤, where

  1. (g)

    the metric d is complete,

Then, f is PO.

Corollary 2.7. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.

Let p be a w-distance on (X, d) and suppose that

  1. (a)

    if x, y ∈ X with (x, y)X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;

  2. (b)

    f is increasing or decreasing;

  3. (c)

    there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;

  4. (d)

    (d 1) f is orbitally continuous or

(d2) f is orbitally X≤-continuous and there exists a subsequenceof {fn (x0)} such thatfor any k ∈ N ;

  1. (e)

    there is a comparison function φ : R + → R + such that

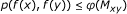
for any (x, y) ∈ X≤, where

  1. (f)

    the metric d is complete,

Then, f is PO.