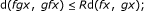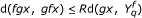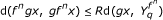Abstract
We prove a common fixed point theorem for four mappings defined on an ordered metric space and apply it to find new common fixed point results. The existence of common fixed points is established for two or three noncommuting mappings where T is either ordered S-contraction or ordered asymptotically S-nonexpansive on a nonempty ordered starshaped subset of a hyperbolic ordered metric space. As applications, related invariant approximation results are derived. Our results unify, generalize, and complement various known comparable results from the current literature.
2010 Mathematics Subject Classification:
47H09, 47H10, 47H19, 54H25.
Similar content being viewed by others
1 Introduction
Metric fixed point theory has primary applications in functional analysis. The interplay between geometry of Banach spaces and fixed point theory has been very strong and fruitful. In particular, geometric conditions on underlying spaces play a crucial role for finding solution of metric fixed point problems. Although, it has purely metric flavor, it is still a major branch of nonlinear functional analysis with close ties to Banach space geometry, see for example [1–4] and references mentioned therein. Several results regarding existence and approximation of a fixed point of a mapping rely on convexity hypotheses and geometric properties of the Banach spaces. Recently, Khamsi and Khan [5] studied some inequalities in hyperbolic metric spaces, which lay foundation for a new mathematical field: the application of geometric theory of Banach spaces to fixed point theory. Meinardus [6] was the first to employ fixed point theorem to prove the existence of invariant approximation in Banach spaces. Subsequently, several interesting and valuable results have appeared about invariant approximations [7–9].
Existence of fixed points in ordered metric spaces was first investigated in 2004 by Ran and Reurings [10], and then by Nieto and Lopez [11].
In 2009, Dorić [12] proved some fixed point theorems for generalized (ψ, φ)-weakly contractive mappings in ordered metric spaces. Recently, Radenović and Kadelburg [13] presented a result for generalized weak contractive mappings in ordered metric spaces (see also, [14, 15] and references mentioned theirin). Several authors studied the problem of existence and uniqueness of a fixed point for mappings satisfying different contractive conditions (e.g., [16–18, 13, 19]). The aim of this article is to study common fixed points of (i) four mappings on an ordered metric space (ii) ordered C q -commuting mappings in the frame work of hyperbolic ordered metric spaces. Some results on invariant approximation for these mappings are also established which in turn extend and strengthen various known results.
2 Preliminaries
Let (X, d) be a metric space. A path joining x ∈ X to y ∈ X is a map c from a closed interval [0, l] ⊂ ℝ to X such that c(0) = x, c(l) = y, and d(c(t), c(t')) = |t - t'| for all t, t' ∈ [0, l]. In particular, c is an isometry and d(x, y) = l. The image of c is called a metric segment joining x and y. When it is unique the metric segment is denoted by [x, y]. We shall denote by (1 - λ)x ⊕ λy the unique point z of [x, y] which satisfies

Such metric spaces are usually called convex metric spaces (see Takahashi [20] and Khan at el. [21]). Moreover, if we have for all p, x, y in X

then X is called a hyperbolic metric space. It is easy to check that in this case for all x, y, z, w in X and λ ∈ [0, 1]

Obviously, normed linear spaces are hyperbolic spaces [5]. As nonlinear examples one can consider Hadamard manifolds [2], the Hilbert open unit ball equipped with the hyperbolic metric [3] and CAT(0) spaces [4].
Let X be a hyperbolic ordered metric space. Throughout this article, we assume that (1 - λ)x ⊕ λy ≤ (1 - λ)z ⊕ λw for all x, y, z, w in X with x ≤ z and y ≤ w. A subset Y of X is said to be ordered convex if Y includes every metric segment joining any two of its comparable points. The set Y is said to be an ordered q-starshaped if there exists q in Y such that Y includes every metric segment joining any of its point comparable with q.
Let Y be an ordered q-starshaped subset of X and f, g : Y → Y. Put,

Set, for each x in X comparable with q in Y,  .
.
Definition 2.1. A selfmap f on an ordered convex subset Y of a hyperbolic ordered metric space X is said to be affine if

for all comparable elements x, y ∈ Y , and λ ∈ [0, 1].
Let f and g be two selfmaps on X. A point x ∈ X is called (1) a fixed point of f if f(x) = x; (2) coincidence point of a pair (f, g) if fx = gx; (3) common fixed point of a pair (f, g) if x = fx = gx. If w = fx = gx for some x in X, then w is called a point of coincidence of f and g. A pair (f, g) is said to be weakly compatible if f and g commute at their coincidence points.
We denote the set of fixed points of f by Fix(f).
Definition 2.2. Let (X, ≤) be an ordered set. A pair (f, g) on X is said:
-
(i)
weakly increasing if for all x ∈ X, we have fx ≤ gfx and gx ≤ fgx, ([22])
-
(ii)
partially weakly increasing if fx ≤ gfx, for all x ∈ X.
Remark 2.3. A pair (f, g) is weakly increasing if and only if ordered pair (f, g) and (g, f) are partially weakly increasing.
Example 2.4. Let X = [0, 1] be endowed with usual ordering. Let f, g : X → X be defined by fx = x2 and  . Then fx = x2 ≤ x = gfx for all x ∈ X. Thus (f, g) is partially weakly increasing. But
. Then fx = x2 ≤ x = gfx for all x ∈ X. Thus (f, g) is partially weakly increasing. But  for x ∈ (0, 1). So (g, f) is not partially weakly increasing.
for x ∈ (0, 1). So (g, f) is not partially weakly increasing.
Definition 2.5. Let (X, ≤) be an ordered set. A mapping f is called weak annihilator of g if fgx ≤ x for all x ∈ X.
Example 2.6. Let X = [0, 1] be endowed with usual ordering. Define f, g : X → X by fx = x2 and gx = x3. Then fgx = x6 ≤ x for all x ∈ X. Thus f is a weak annihilator of g.
Definition 2.7. Let (X, ≤) be an ordered set. A selfmap f on X is called dominating map if x ≤ fx for each x in X.
Example 2.8. Let X = [0, 1] be endowed with usual ordering. Let f : X → X be defined by  . Then
. Then  for all x ∈ X. Thus f is a dominating map.
for all x ∈ X. Thus f is a dominating map.
Example 2.9. Let X = [0, ∞) be endowed with usual ordering. Define f : X → X by

n ∈ N. Then for all x ∈ X, x ≤ fx so that f is a dominating map.
Definition 2.10. Let (X, ≤) be a ordered set and f and g be selfmaps on X. Then the pair (f, g) is said to be order limit preserving if

for all sequences {x n } in X with gx n ≤ fx n and x n → x0.
Definition 2.11. Let X be a hyperbolic ordered metric space, Y an ordered q-starshaped subset of X, f and g be selfmaps on X and q ∈ Fix(g). Then f is said to be:
-
(1)
ordered g-contraction if there exists k ∈ (0, 1) such that
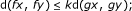
for x, y ∈ Y with x ≤ y.
-
(2)
ordered asymptotically S-nonexpansive if there exists a sequence {k n }, k n ≥ 1, with
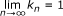 such that
such that
for each x, y in Y with x ≤ y and each n ∈ N. If k n = 1, for all n ∈ N , then f is known as ordered g-nonexpansive mapping. If g = I (identity map), then f is ordered asymptotically nonexpansive mapping;
-
(3)
R-weakly commuting if there exists a real number R > 0 such that
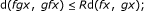
for all x in Y.
-
(4)
ordered R-subweakly commuting [23] if there exists a real number R > 0 such that
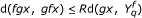
for all x ∈ Y.
-
(5)
ordered uniformly R-subweakly commuting [23] if there exists a real number R > 0 such that
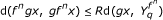
for all x ∈ Y.
-
(6)
ordered C q -commuting [24], if gfx = fgx for all x ∈ C q (f, g), where C q (f, g) = U {C(g, fk) : 0 ≤ k ≤ 1} and f k x = (1 - k)q ⊕ kfx.
-
(7)
ordered uniformly C q -commuting, if gf nx = f ngx for all x ∈ C q (g, f n) and n ∈ N.
-
(8)
uniformly asymptotically regular on Y if, for each η > 0, there exists N(η) = N such that d(f nx, f n+1x) < η for all η ≥ N and all x ∈ Y .
For other related notions of noncommuting maps, we refer to [7]; in particular, here Example 2.2 and Remark 3.10(2) provide two maps which are not C q -commuting. Also, uniformly C q -commuting maps on X are C q -commuting and uniformly R-subweakly commuting maps are uniformly C q -commuting but the converse statements do not hold, in general [23, 25]. Fixed point theorems in a hyperconvex metric space (an example of a convex metric space) have been established by Khamsi [26] and Park [27].
Let Y be a closed subset of an ordered metric space X. Let x ∈ X. Define d(x, Y ) = inf{d(x, y) : y ∈ Y, y ≤ x or x ≤ y}. If there exists an element y0 in Y comparable with x such that d(x, y0) = d(x, Y ), then y0 is called an ordered best approximation to X out of Y. We denote by P Y (x), the set of all ordered best approximation to x out of Y. The reader interested in the interplay of fixed points and approximation theory in normed spaces is referred to the pioneer work of Park [28] and Singh [9].
3 Common fixed point in ordered metric spaces
We begin with a common fixed point theorem for two pairs of partially weakly increasing functions on an ordered metric space. It may regarded as the main result of this article.
Theorem 3.1. Let (X, ≤, d) be an ordered metric space. Let f, g, S, and T be selfmaps on X, (T, f) and (S, g) be partially weakly increasing with f(X) ⊆ T(X), g(X) ⊆ S(X), and dominating maps f and g be weak annihilator of T and S, respectively. Also, for every two comparable elements x, y ∈ X,

where

for h ∈ [0, 1) is satisfied. If one of f(X), g(X), S(X), or T(X) is complete subspace of X, then {f, S} and {g, T} have unique point of coincidence in X provided that for a nondecreasing sequence {x n } with x n ≤ y n for all n and y n → u implies x n ≤ u. Moreover, if {f, S} and {g, T } are weakly compatible, then f, g, S, and T have a common fixed point.
Proof. For any arbitrary point x0 in X, construct sequences {x n } and {y n } in X such that

Since dominating maps f and g are weak annihilator of T and S, respectively so for all n ≥ 1,

and

Thus, we have x n ≤ xn+1for all n ≥ 1. Now (3.1) gives that.

for n = 1, 2, 3,..., where

Now if M(x2n, x2n+1) = d(y2n, y2n+1), then d(y2n+1, y2n+2) ≤ h d(y2n, y2n+1).
And if M(x2n, x2n+1) = d(y2n+1, y2n+2), then d(y2n+1, y2n+2) ≤ h d(y2n+1, y2n+2)
which implies that d(y2n+1, y2n+2) = 0, and y2n+1= y2n+2. Hence

Therefore

for all n ∈ ℕ. Then, for m > n,

and so d(y n , y m ) → 0 as n, m → ∞. Hence {y n } is a Cauchy sequence. Suppose that S(X) is complete. Then there exists u in S(X), such that Sx2n= y2n→ u as n → ∞. Consequently, we can find v in X such that Sv = u. Now we claim that fv = u. Since, x2n-2≤ x2n-1≤ gx2n-1= Sx2-nand Sx2n→ Sv. So that x2n-1≤ Sv and since, Sv ≤ gSv and gSv ≤ v, implies x2n-1≤ v. Consider

where

for all n ∈ ℕ. Now we have four cases:
If M(v, x2n-1) = d(Sv, Tx2n-1), then d(fv, u) ≤ h d(Sv, Tx2n-1)+d(gx2n-1,u) → 0 as n → ∞ implies that fv = u.
If M(v, x2n-1) = d(fv, Sv), then d(fv, u) ≤ h d(fv, Sv) + d(gx2n-1,u). Taking limit as n → ∞ we get d(fv, u) ≤ h d(fv, u). Since h < 1, so that fv = u.
If M(v, x2n-1) = d(gx2n-1,Tx2n-1), then d(fv, u) ≤ h d(gx2n-1,Tx2n-1) + d(gx2n-1,u) → 0 as n → ∞ implies that fv = u.
If  , then
, then

Taking limit as n → ∞ we get  . Since h < 1, so that fv = u. Therefore, in all the cases fv = Sv = u.
. Since h < 1, so that fv = u. Therefore, in all the cases fv = Sv = u.
Since u ∈ f(X) ⊂ T(X), there exists w ∈ X such that Tw = u. Now we shall show that gw = u. As, x2n-1≤ x2n≤ fx2n= Tx2n+1and Tx2n+1→ Tw and so x2n≤ Tw. Hence, Tw ≤ fTw and fTw ≤ w, imply x2n≤ w. Consider

where
 for all n ∈ ℕ.
for all n ∈ ℕ.
Again we have four cases:
If M(x2n,w) = d(Sx2n,Tw), then d(gw, u) ≤ h d(Sx2n,Tw) + d(fx2n,u) → 0 as n → ∞.
If M(x2n,w) = d(fx2n,Sx2n), then d(gw, u) ≤ h d(fx2n,Sx2n) + d(fx2n,u) → 0 as n → ∞.
If M(x2n,w) = d(gw, Tw), then d(gw, u) ≤ h d(gw, Tw)+d(fx2n,u) = h d(gw, u)+ d(fx2n,u). Taking limit as n → ∞ we get d(gw, u) ≤ h d(gw, u) which implies that gw = u. If  , then
, then

Taking limit as n → ∞ we get  which implies that gw = u. Following the arguments similar to those given above, we obtain gw = Tw = u. Thus {f, S} and {g, T} have a unique point of coincidence in X. Now, if {f, S} and {g, T} are weakly compatible, then fu = fSv = Sfv = Su = w1 (say) and gu = gTw = Tgw = Tu = w 2 (say). Now
which implies that gw = u. Following the arguments similar to those given above, we obtain gw = Tw = u. Thus {f, S} and {g, T} have a unique point of coincidence in X. Now, if {f, S} and {g, T} are weakly compatible, then fu = fSv = Sfv = Su = w1 (say) and gu = gTw = Tgw = Tu = w 2 (say). Now

where

Therefore d(w1, w2) ≤ h d(w1, w2) gives w1 = w2. Hence

That is, u is a coincidence point of f, g, S,, and T. Now we shall show that u = gu. Since, v ≤ fv = u,

where

Thus, d(u, gu) ≤ h d(u, gu) implies that gu = u. In similar way, we obtain fu = u. Hence, u is a common fixed point of f, g, S, and T.
In the following result, we establish existence of a common fixed point for a pair of partially weakly increasing functions on an ordered metric space by using a control function r : R+ → R+.
Theorem 3.2. Let (X, ≤, d) be an ordered metric space. Let f and g be R-weakly commuting selfmaps on X, (g, f) be partially weakly increasing with f(X) ⊆ g(X), dominating map f is weak annihilator of g. Suppose that for every two comparable elements x, y ∈ X,

where r : R+ → R+ is a continuous function such that r(t) < t for each t > 0. If either f or g is continuous and one of f(X) or g(X) is complete subspace of X, then f and g have a common fixed point provided that for a nondecreasing sequence {x n } with x n ≤ y n for all n and y n → u implies x n ≤ u.
Proof. Let x0 be an arbitrary point in X. Choose a point x1 in X such that

Since dominating map f is weak annihilator of g, so that for all n ≥ 1,

Thus, we have x n ≤ x n +1 for all n ≥ 1. Now

Thus {d(fx n , fxn+1)} is a decreasing sequence of positive real numbers and, therefore, tends to a limit L. We claim that L = 0. For if L > 0, the inequality

on taking limit as n → ∞ and in the view of continuity of r yields L ≤ r(L) < L, a contradiction. Hence, L = 0.
For a given ε > 0, since r(ε) < ε, there is an integer k0 such that

For m, n ∈ N with m > n, we claim that

We prove inequality (3.3) by induction on m. Inequality (3.3) holds for m = n + 1, using inequality (3.2) and the fact that ε - r (ε) < ε. Assume inequality (3.3) holds for m = k. For m = k + 1, we have

By induction on m, we conclude that inequality (3.3) holds for all m ≥ n ≥ k0.
So {fx n } is a Cauchy sequence. Suppose that g(X) is a complete metric space. Hence {fx n } has a limit z in g(X). Also gx n → z as n → ∞.
Let us suppose that the mapping f is continuous. Then ffx n → fz and fgx n → fz. Further, since f and g are R - weakly commuting, we have

Taking limit as n → ∞, the above inequality yields gffx n → fz. We now assert that z = fz. Otherwise, since x n ≤ fx n , so we have the inequality

Taking limit as n → ∞ gives d(z, fz) ≤ r(d(z, fz)) < d(z, fz), a contradiction.
Hence, z = fz. As f(X) ⊆ g(X), there exists z1 in X such that z = fz = gz1.
Now, since fx n ≤ ffx n and ffxn → fz = gz1 and gz1 ≤ fgz1 ≤ z1 imply fx n ≤ z1. Consider,

Taking limit as n → ∞ implies that fz = fz1. This in turn implies that

i.e., z = fz = gz. Thus z is a common fixed point of f and g. The same conclusion is found when g is assumed to be continuous since continuity of g implies continuity of f.
4 Results in hyperbolic ordered metric spaces
In this section, existence of common fixed points of ordered C q -commuting and ordered uniformly C q -commuting mappings is established in hyperbolic ordered metric spaces by utilizing the notions of ordered S-contractions and ordered asymptotically S-nonexpansive mappings.
Theorem 4.1. Let Y be a nonempty closed ordered subset of a hyperbolic ordered metric space X. Let T and S be ordered R- subweakly commuting selfmaps on Y such that T(Y ) ⊂ S(Y ), cl(T(Y )) is compact, q ∈ Fix(S) and S(Y ) is complete and q-starshaped where each x in X is comparable with q. Let (T, S) be partially weakly increasing, order limit preserving and weakly compatible pair such that dominating map T is weak annihilator of S. If T is continuous, S-ordered nonexpansive and S is affine, then Fix(T) ∩ Fix(S) is nonempty provided that for a nondecreasing sequence {x n } with x n → u implies that x n ≤ u.
Proof. Define T n : Y → Y by

for each n ≥ 1, where λ
n
∈ (0, 1) with  . Then T
n
is a selfmap on Y for each n ≥ 1. Since S is ordered affine and T(Y ) ⊂ S(Y ), therefor we obtain T
n
(Y ) ⊂ S(Y ). Note that,
. Then T
n
is a selfmap on Y for each n ≥ 1. Since S is ordered affine and T(Y ) ⊂ S(Y ), therefor we obtain T
n
(Y ) ⊂ S(Y ). Note that,

This implies that the pair {T n , S} is ordered λ n R-weakly commuting for each n. Also for any two comparable elements x and y in X, we get

Now following lines of the proof of Theorem 3.2, there exists x n in Y such that x n is a common fixed point of S and T n for each n ≥ 1. Note that

Since cl(T(Y )) is compact, there exists a positive integer M such that

The compactness of cl(T n (Y )) implies that there exists a subsequence {x k } of {x n } such that x k → x0 ∈ Y as k → ∞. Now,

and continuity of T give that x0 ∈ Fix(T). Since, T is dominating map, therefore Sx k ≤ TSx k . As T is weak annihilator of S and T is dominating, so TSx k ≤ x k ≤ Tx k . Thus Sx k ≤ Tx k and order limit preserving property of (T, S) implies that Sx0 ≤ Tx0 = x0. Also x0 ≤ Sx0. Consequently, Sx0 = Tx0 = x0. Hence the result follows.
Theorem 4.2. Let Y be a nonempty closed subset of a complete hyperbolic ordered metric space X and let T and S be mappings on Y such that T(Y - {u}) ⊂ S(Y - {u}), where u ∈ Fix(S). Suppose that T is an S-contraction and continuous. Let (T, S) be partially weakly increasing, dominating maps T is weak annihilator of S. If T is continuous, and S and T are R-weakly commuting mappings on Y - {u}, then Fix(T)∩Fix(S) is nonempty provided that for a nondecreasing sequence {x n } with x n ≤ y n for all n and y n → u implies x n ≤ u.
Proof. Similar to the proof of Theorem 3.2.
Theorem 3.1 yields a common fixed point result for a pair of maps on an ordered startshaped subset Y of a hyperbolic ordered metric space as follows.
Theorem 4.3. Let Y be a nonempty closed q- starshaped subset of a complete hyperbolic ordered metric space X and let T and S be uniformly C
q
- commuting selfmapps on Y - {q} such that S(Y ) = Y and T(Y - {q}) ⊂ S(Y - {q}), where q ∈ Fix(S). Let (T, S) be partially weakly increasing, order limit preserving and weakly compatible pair, dominating map T is weak annihilator of S, T is continuous and asymptotically S- nonexpansive with sequence {k
n
}, as in Definition 2.11 (2), and S is an affine mapping. For each n ≥ 1, define a mapping T
n
on Y by T
n
x = (1 - α
n
)q ⊕ α
n
T nx, where  and {λ
n
} is a sequence in (0, 1) with
and {λ
n
} is a sequence in (0, 1) with  . Then for each n ∈ N, F (T
n
) ∩ Fix(S) is nonempty provided that for a nondecreasing sequence {x
n
} with x
n
≤ y
n
for all n and y
n
→ u implies x
n
≤ u.
. Then for each n ∈ N, F (T
n
) ∩ Fix(S) is nonempty provided that for a nondecreasing sequence {x
n
} with x
n
≤ y
n
for all n and y
n
→ u implies x
n
≤ u.
Proof. For all x, y ∈ Y, we have

Moreover, since T and S are uniformly C q -commuting and S is affine on Y with Sq = q, for each x ∈ C n (S, T ) ⊆ C q (S, T ), we have

Thus S and T n are weakly compatible for all n. Now, the result follows from Theorem 3.1.
The above theorem leads to the following result.
Theorem 4.4. Let Y be a nonempty closed q- starshaped subset of a hyperbolic ordered metric space X and let T and S be selmaps on Y such that S(Y ) = Y and T(Y - {q}) ⊂ S(Y - {q}), q ∈ Fix(S). Let (T, S) be partially weakly increasing, order limit preserving, T is continuous, uniformly asymptotically regular, asymptotically S-nonexpansive and S is an affine mapping. If cl(Y - {q}) is compact and S and T are uniformly C q -commuting selfmaps on Y - {q}, then Fix(T) ∩ Fix(S) is nonempty provided that for a nondecreasing sequence {x n } with x n ≤ yn for all n and y n → u implies x n ≤ u.
Proof. By Theorem 4.3, for each n ∈ N, F(T n ) ∩ Fix(S) is singleton in Y. Thus,

Also,

Since T(Y - {q}) is bounded so d(x n , T nx n ) → 0 as n → ∞. Note that,

Consequently, d(x
n
, Tx
n
) → 0, when n → ∞. Since cl(Y - {q}) is compact and Y is closed, therefore there exists a subsequence  of {x
n
} such that
of {x
n
} such that  as i → ∞. By the continuity of T , we have T(x0) = x0. Since, T is dominating map, therefore Sx
k
≤ TSx
k
. As T is weak annihilator of S and T is dominating, so TSx
k
≤ x
k
≤ Tx
k
. Thus, Sx
k
≤ Tx
k
and order limit preserving property of (T, S) implies that Sx0 ≤ Tx0 = x0. Also x0 ≤ Sx0. Consequently, Sx0 = Tx0 = x0. Hence, the result follows.
as i → ∞. By the continuity of T , we have T(x0) = x0. Since, T is dominating map, therefore Sx
k
≤ TSx
k
. As T is weak annihilator of S and T is dominating, so TSx
k
≤ x
k
≤ Tx
k
. Thus, Sx
k
≤ Tx
k
and order limit preserving property of (T, S) implies that Sx0 ≤ Tx0 = x0. Also x0 ≤ Sx0. Consequently, Sx0 = Tx0 = x0. Hence, the result follows.
As another application of Theorem 3.1, we obtain yet an other result for two maps satisfying a very general contractive condition on the set Y.
Theorem 4.5. Let Y be a nonempty q-starshaped complete subset of a hyperbolic ordered metric space and T, f, and g be selfmaps on Y . Suppose that T is continuous, cl(T(Y )) is compact and f and g are affine and continuous and T(Y ) ⊂ f(Y ) ∩g(Y ). Let (T, f) and (T, g) be partially weakly increasing, and dominating maps f and g be weak annihilators of T. If the pairs {T, f} and {T, g} are C q -commuting and satisfy for all x, y ∈ Y,

then T, f, and g have a common fixed point provided that for a nondecreasing sequence {x n } with x n ≤ y n for all n and y n → u implies x n ≤ u.
Proof. Define T n : Y → Y by

where λ
n
∈ (0, 1) with  . Then T
n
is a selfmap on Y for each n ≥ 1. Since f and g are affine and T(Y ) ⊂ f(Y ) ∩ g(Y ), therefore we obtain T
n
(Y ) ⊂ f (Y ) ∩ g(Y ). Now f and T are C
q
-commuting and f is affine on Y with fq = q, for each x ∈ C
n
(f, T ) ⊆ C
q
(f, T ), so we have
. Then T
n
is a selfmap on Y for each n ≥ 1. Since f and g are affine and T(Y ) ⊂ f(Y ) ∩ g(Y ), therefore we obtain T
n
(Y ) ⊂ f (Y ) ∩ g(Y ). Now f and T are C
q
-commuting and f is affine on Y with fq = q, for each x ∈ C
n
(f, T ) ⊆ C
q
(f, T ), so we have

Thus, f and T n are weakly compatible for all n. Also since g and T are C q -commuting and g is affine on Y with gq = q, therefore, g and T n are weakly compatible for all n. Moreover using (4.1) we have

By Theorem 3.1, for each n ≥ 1, there exists x n in Y such that x n is a common fixed point of f, g and T n . The compactness of cl(T (Y )) implies that there exists a subsequence {Tx k } of {Tx n } such that Tx k → y as k → ∞. Now, the definition of T k x k gives that x k → y and the result follows using continuity of T, f, and g.
5 Invariant approximation
In this section, we obtain results on best approximation as a fixed point of R-subweakly and uniformly R-subweakly commuting mappings in the setting of hyperbolic ordered metric spaces. In particular, as an application of Theorem 4.4 (respectively Theorem 4.5), we demonstrate the existence of common fixed point for one pair (respectively two pairs) of maps from the set of best approximation.
Theorem 5.1. Let M be a nonempty subset of a hyperbolic ordered metric space X, T, and S be continuous selfmaps on X such that T(∂M ∩ M) ⊂ M, ∂M stands for boundary of M, and u ∈ Fix(S) ∩ Fix(T) for some u in X, where u is comparable with all x ∈ X. Let (T, S) be partially weakly increasing, order limit preserving, T is uniformly asymptotically regular, asymptotically S-nonexpansive and S is affine on P M (u) with S(P M (u)) = P M (u), q ∈ Fix(S), and P M (u) is q-starshaped. If cl(P M (u)) is compact, P M (u) is complete and S and T are uniformly C q -commuting mappings on P M (u) ∪ {u} satisfying d(Tx, Tu) ≤ d(Sx, Su), then P M (u) ∩ Fix(T ) ∩ Fix(S) ≠ ϕ provided that for a nondecreasing sequence {x n } with x n ≤ y n for all n and y n → u implies x n ≤ u.
Proof. Let x ∈ P M (u). Then d(x, u) = d(u, M ). Note that for any λ ∈ (0, 1),

This shows that  . So x ∈ ∂M ∩ M which further implies that Tx ∈ M. Since Sx ∈ P
M
(u), u is a common fixed point of S and T, therefore by the given contractive condition, we obtain
. So x ∈ ∂M ∩ M which further implies that Tx ∈ M. Since Sx ∈ P
M
(u), u is a common fixed point of S and T, therefore by the given contractive condition, we obtain

Thus, P M (u) is T -invariant. Hence,

Now the result follows from Theorem 4.4.
Theorem 5.2. Let M be a nonempty subset of a hyperbolic ordered metric space X, T, f, and g be selfmaps on X such that u is common fixed point of f, g, and T and T(∂M ∩ M) ⊂ M. Suppose that f and g are continuous and affine on P M (u), q ∈ Fix(f ) ∩ Fix(g), and P M (u) is q-starshaped with f(P M (u)) = P M (u) = g(P M (u)). Let (T, f ) and (T, g) be partially weakly increasing, and dominating maps f and g be weak annihilator of T. Assume that the pairs {T, f} and {T, g} are C q -commuting and satisfy for all x ∈ P M (u) ∪ {u}

If cl(P M (u)) is compact and P M (u) is complete, then P M (u)∩Fix(T )∩Fix(f )∩ Fix(g) ≠ ϕ provided that for a nondecreasing sequence {x n } with x n ≤ y n for all n and y n → u implies x n ≤ u.
Proof. Let x ∈ P M (u). Then d(x, u) = d(u, M ). Note that for any λ ∈ (0, 1)

which shows that M and  are disjoint. So x ∈ ∂M ∩ M which further implies that Tx ∈ M. Since fx ∈ P
M
(u), u is a common fixed point of f, g, and T, therefore by the given contractive condition, we obtain
are disjoint. So x ∈ ∂M ∩ M which further implies that Tx ∈ M. Since fx ∈ P
M
(u), u is a common fixed point of f, g, and T, therefore by the given contractive condition, we obtain

Thus P M (u) is T -invariant. Hence,

The result follows from Theorem 4.5.
Remark 5.3.
-
(a)
Theorem 3.2 extends and improves Theorem 2.2 of Al-Thagafi [8] and Theorem 2.2(i) of Hussain and Jungck [25] in the setup of hyperbolic ordered metric spaces.
-
(b)
Theorems 4.4 and 4.5 extend the results in [23] to more general classes of mappings defined on a hyperbolic ordered metric space.
-
(c)
Theorems 5.1 and 5.2 set analogues of Theorems 2.11(i) and 2.12(i) in [25], respectively.
References
Bridson M, Haefliger A: Metric Spaces of Non-Positive Curvature. Springer, Berlin, Heidelberg; 1999.
Busemann H: Spaces with non positive curvature. Acta Math 1984, 80: 259–310.
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry and Gonexpansive Mappings. Marcel Dekker, Inc., New York; 1984.
Kirk WA: Fixed point theory for nonexpansive mappings, I and II. In Lecture Notes in Mathematics. Volume 886. Springer, Berlin; 1981:485–405.
Khamsi MA, Khan AR: Inequalities in metric spaces with applications. Nonlinear Analy 2011, 74: 4036–4045. 10.1016/j.na.2011.03.034
Meinardus G: Invarianz bei linearn approximation. Arch. Ration. Mech. Anal 1963, 14: 301–303.
Akbar F, Khan AR: Common fixed point and approximation results for noncommuting maps on locally convex spaces. Fixed Point Theory Appl 2009, 14. (Article ID 207503)
Al-Thagafi MA: Common fixed points and best approximation. J. Approx. Theory 1996, 85: 318–320. 10.1006/jath.1996.0045
Singh SP: Application of a fixed point theorem to approximation theory. J Approx Theory 1979, 25: 88–89.
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some application to matrix equations. Proc. Amer. Math. Soc 2004, 132: 1435–1443. 10.1090/S0002-9939-03-07220-4
Nieto JJ, Lopez RR: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005, 22: 223–239. 10.1007/s11083-005-9018-5
Dorić D: Common fixed point for generalized ( ψ , φ )-weak contractions. Appl. Math. Lett 2009, 22: 1896–1900. 10.1016/j.aml.2009.08.001
Radenović S, Kadelburg Z: Generalized weak contractions in partially ordered metric spaces. Comput. Math. Appl 2010, 60: 1776–1783. 10.1016/j.camwa.2010.07.008
Saadati R, Vaezpour SM: Monotone generalized weak contractions in partially ordered metric spaces. Fixed Point Theory 2010, 11: 375–382.
Saadati R, Vaezpour SM, Vetro P, Rhoades BE: Fixed point theorems in generalized partially ordered G-metric spaces. Math. Comput. Model 2010, 52: 797–801. 10.1016/j.mcm.2010.05.009
Amini-Harandi A, Emami H: A fixed point theorem for contraction type maps in partially ordered metric spaces and application to ordinary differential equations. Nonlinear Anal 2010, 72: 2238–2242. 10.1016/j.na.2009.10.023
Beg I, Abbas M: Coincidence point and invariant approximation for mappings satisfying generalized weak contractive condition. Fixed Point Theory Appl 2006: 7. (Article ID 74503)
Harjani J, Sadarangani K: Fixed point theorems for weakly contractive mappings in partially ordered sets. Nonlinear Anal 2009, 71: 3403–3410. 10.1016/j.na.2009.01.240
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Anal 2001, 47: 2683–2693. 10.1016/S0362-546X(01)00388-1
Takahashi W: A convexity in metric space and nonexpansive mappings. Kodai Math. Sem. Rep 1970, 22: 142–149. 10.2996/kmj/1138846111
Khan AR, Fukhar-ud-din H, Domlo AA: Approximating fixed points of some maps in uniformly convex metric spaces. Fixed Point Theory Appl 2010: 11. (Article ID 385986)
Altun I, Damjanovic B, Djoric D: Fixed point and common fixed point theorems on ordered cone metric spaces. Appl. Math. Lett 2010, (23):310–316.
Beg I, Sahu DR, Diwan SD: Approximation of fixed points of uniformly R -subweakly commuting mappings. J. Math. Anal. Appl 2006, 324: 1105–1114. 10.1016/j.jmaa.2006.01.024
Hussain N, Rhoades BE: C q -commuting maps and invariant approximations. Fixed Point Theory Appl 2006: 9. (Article ID 24543)
Hussain N, Jungck G: Common fixed point and invariant approximation results for noncommuting generalized ( f , g )-nonexpansive maps. J. Math. Anal. Appl 2006, 321: 851–861. 10.1016/j.jmaa.2005.08.045
Khamsi MA: KKM and Ky Fan theorems in hyperconvex metric spaces. J. Math. Anal. Appl 1996, 204: 298–306. 10.1006/jmaa.1996.0438
Park S: Fixed point theorems in hyperconvex metric spaces. Nonlinear Anal 1999, 37: 467–472. 10.1016/S0362-546X(98)00061-3
Park S: Best approximations, inward sets and fixed points. In Progress in Approximation Theory. Acedemic Press, Inc; 1991:711–719.
Acknowledgements
The second and third authors are grateful to King Fahd University of Petroleum and Minerals and SABIC for supporting research project SB100012.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
The authors have contributed in this work on an equal basis. All authors have read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abbas, M., Khamsi, M.A. & Khan, A.R. Common fixed point and invariant approximation in hyperbolic ordered metric spaces. Fixed Point Theory Appl 2011, 25 (2011). https://doi.org/10.1186/1687-1812-2011-25
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-25



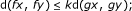
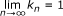 such that
such that