Abstract
With the popularity of group-oriented applications, secure group communication has recently received much attention from cryptographic researchers. A group key exchange (GKE) protocol allows that participants cooperatively establish a group key that is used to encrypt and decrypt transmitted messages. Hence, GKE protocols can be used to provide secure group communication over a public network channel. However, most of the previously proposed GKE protocols deployed in wired networks are not fully suitable for wireless network environments with low-power computing devices. Subsequently, several GKE protocols suitable for mobile or wireless networks have been proposed. In this article, we will propose a more efficient group key exchange protocol with dynamic joining and leaving. Under the decision Diffie-Hellman (DDH), the computation Diffie-Hellman (CDH), and the hash function assumptions, we demonstrate that the proposed protocol is secure against passive attack and provides forward/backward secrecy for dynamic member joining/leaving. As compared with the recently proposed GKE protocols, our protocol provides better performance in terms of computational cost, round number, and communication cost.
Similar content being viewed by others
Introduction
Wireless communication technology has widely been applied to many mobile applications and services such as e-commerce applications, mobile access services, and wireless Internet services. Nowadays, people use their cellular phone or PDA (personal digital assistant) to access these mobile services. However, most of such security schemes and protocols deployed in wired networks are not fully applicable to wireless networks (i.e., wireless local area networks [1], mobile ad hoc networks [2], cellular mobile networks [3], and wireless sensor networks [4]) because of the network architecture and the computational complexity of mobile devices. In addition, an intruder is easy to intercept the transmitted messages over a wireless network because wireless communications use radio waves to transmit messages. Meanwhile, most cryptographic algorithms require many expensive computations, thus it will be a nontrivial challenge to design security schemes and protocols for wireless network environments with low-power computing devices [5, 6].
With the popularity of group-oriented applications such as collaboration works and electric conferences, secure group communication has received much attention from cryptographic researchers. A group key exchange (GKE) protocol allows that participants establish a group key to encrypt/decrypt the transmitted messages. Thus, GKE protocols can be used to provide secure group communication. In 1982, Ingemaresson et al. [7] proposed the first GKE protocol relied on the two-party Diffie-Hellman scheme [8]. Subsequently, different types of GKE protocols were presented such as constant-round GKE [9–13] and linear-round GKE [14–17]. However, these previously proposed GKE protocols did not deal with the computing capability of mobile devices in wireless mobile networks.
Actually, considering wireless network environments such as wireless local area networks [1] and cellular mobile networks [3], they may be regarded as asymmetric (imbalanced) wireless networks. An imbalanced wireless network consists of mobile clients and a powerful node. Generally, mobile clients may use some mobile devices (i.e., cellular phone or PDA) to access mobile applications through the powerful node. If such mobile clients want to perform a secure conference using their mobile devices through cellular mobile networks or wireless local area networks, they must establish a secure group key to encrypt/decrypt the transmitted messages. Considering the computing capability of mobile devices, a flexible approach is to shift the computational burden from the mobile devices to the powerful node. This approach reduces the computational costs on mobile nodes. Consequently, several group key agreement protocols [18–22] for the imbalanced wireless network have been proposed.
In 2003, Boyd and Nieto [18] presented a one-round GKE protocol. Their protocol is efficient for imbalanced wireless networks, but it lacks forward secrecy. Bresson et al. [19] proposed a two-round GKE protocol for imbalanced wireless networks. Unfortunately, their protocol provides only partial forward secrecy [20]. This partial forward secrecy means that leaking the mobile nodes' private keys do not reveal any information about the previous establishment group keys, but leaking the powerful node's private key will enable an adversary to reconstruct the previous group keys. Subsequently, Nam et al. [20] also presented an improvement on the protocol proposed by Bresson et al. In 2007, Tseng [21] demonstrated that the Nam et al.'s protocol has a security weakness. In their protocol, the powerful node can pre-determine the group key. That is, Nam et al.'s protocol is not a contributory GKE protocol. For repairing this weakness, Tseng also proposed a secure group key exchange protocol for imbalanced wireless networks. However, Tseng's GKE protocol does not deal with dynamic member joining/leaving functionality. Note that the dynamic joining/leaving functionality means that other participants need not to re-run the protocol when a participant joins or leaves the group. For a GKE protocol, it is important to provide this dynamic functionality, especially for wireless network environments. For providing dynamic joining/leaving functionality, Chuang and Tseng [22] recently proposed a dynamic group key exchange protocol for imbalanced wireless networks. However, their protocol requires three rounds to establish a group key.
Since the recently proposed GKE protocols [20–22] for wireless network environment are non-authenticated ones. By its very nature, a non-authenticated group key exchange protocol cannot provide participant and message authentication, so it must rely on the authenticated network channel [1, 3] or use other schemes [23–25] to provide authentication in advance. Here, as like the recently proposed GKE protocols [20–22], we assume that each mobile client and the powerful node have already authenticated mutually. Here, we focus on the design of a non-authenticated GKE protocol. In this article, we propose a new group key exchange protocol with the dynamic property for wireless network environments. Under several security assumptions, we will prove that the proposed protocol is secure against passive attack and provides forward/backward secrecy for dynamic member joining/leaving. Meanwhile, we demonstrate that the proposed protocol also satisfies the contributiveness property. As compared with the recently proposed GKE protocols, our protocol provides better performance in terms of computational cost, round number, and communication cost.
The remainder of this article is organized as follows. In the next section, we present the security assumptions and the security requirements for a dynamic GKE protocol. In 'A concrete dynamic GKE protocol' section, we propose a concrete dynamic GKE protocol. Security analysis of the proposed protocol is demonstrated in 'Security analysis' section. In 'Performance analysis and discussions' section, we make performance analysis and comparisons. The conclusions are given in 'Conclusions' section.
Preliminaries
In this section, we present the security requirements of dynamic group key exchange protocol, as well as several security assumptions.
Notations
The following notations are used throughout the article:
-
p, q: two large primes satisfying p = 2q + 1.
-
G q : a subgroup of Z p * with the order q.
-
g: a generator of the group G q .
-
H: a one-way hash function, H:{0, 1}* → Z q *.
-
SID: a session identity is public information. Note that each session is assigned a unique SID.
Security requirements for dynamic GKE protocol
Here, we define the security requirements of a dynamic GKE protocol as follows:
-
Passive attack: This attack means that a passive adversary cannot compute the group key by eavesdropping on the transmitted messages over a public channel or efficiently distinguish the group key from a random string.
-
Forward secrecy: When a new member joins the group, he/she cannot compute the previous established group keys to decrypt the past encrypted messages.
-
Backward secrecy: When an old member leaves the group, he/she cannot compute the subsequent group keys to decrypt the future encrypted messages.
-
Contributiveness: In the group, any participants cannot predetermine or predict the resulting group key. In other words, each participant can confirm that her/his contribution has been involved in the group key.
Security of a dynamic GKE protocol
We say that a dynamic group key exchange protocol is secure, if (1) it is secure against passive attack; (2) it provides forward/backward secrecy for joining/leaving; (3) it satisfies contributiveness.
Security assumptions
For the security of our proposed dynamic group key exchange protocol, we need the following hard problems and assumptions [26, 27].
-
Decision Diffie-Hellman (DDH) problem: Given
 and
and 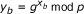 for some x
a
, x
b
∈ Z
q
*, the DDH problem is to distinguish two tuples (y
a
, y
b
,
for some x
a
, x
b
∈ Z
q
*, the DDH problem is to distinguish two tuples (y
a
, y
b
,  ) and (y
a
, y
b
, R ∈ G
q
).
) and (y
a
, y
b
, R ∈ G
q
). -
DDH assumption: There exists no probabilistic polynomial-time algorithm can solve the DDH problem with a non-negligible advantage.
-
Computational Diffie-Hellman (CDH) problem: Given a tuple (g,
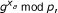
 ) for some x
a
, x
b
∈ Z
q
*, the CDH problem is to compute the value
) for some x
a
, x
b
∈ Z
q
*, the CDH problem is to compute the value 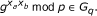
-
CDH assumption: There exists no probabilistic polynomial-time algorithm can solve the CDH problem with a non-negligible advantage.
-
Hash function assumption: A secure one-way hash function
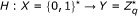 must satisfy following requirements [28]:
must satisfy following requirements [28]:
-
(i)
For any y ∈ Y, it is hard to find x ∈ X such that H(x) = y.
-
(ii)
For any x ∈ X, it is hard to find x' ∈ X such that x' ≠ x and H(x') = H(x).
-
(iii)
It is hard to find x, x' ∈ X such that x ≠ x' and H(x) = H(x').
A concrete dynamic GKE protocol
In this section, we present a new group key exchange protocol with the member joining/leaving functionality. Without loss of generality, let {U0, U1, U2,..., U n } be a set of participants who want to generate a group key in an imbalanced wireless network, where U0 is a powerful node and U1,..., U n are n mobile clients with the limited computing capability. Our proposed dynamic GKE protocol is depicted in Figure 1 and the detailed steps are described as follows.
Step 1: Each client U
i
(1 ≤ i ≤ n) selects a random value  and computes
and computes  . Then, each U
i
sends (U
i
, z
i
) to the powerful node U0.
. Then, each U
i
sends (U
i
, z
i
) to the powerful node U0.
Step 2: The powerful node U0 first selects two random values r0, r ∈ Z
q
* and computes  . Upon receiving n pairs (U
i
, z
i
) (1 ≤ i ≤ n), U0 computes
. Upon receiving n pairs (U
i
, z
i
) (1 ≤ i ≤ n), U0 computes  and y
i
= H(x
i
||SID)⊕r for i = 1, 2,..., n. Finally, the powerful node U0 computes SK = H(r||y1||y2||...||y
n
||SID) and broadcasts (U0, y1, y2,..., y
n
, z0, SID) to all clients.
and y
i
= H(x
i
||SID)⊕r for i = 1, 2,..., n. Finally, the powerful node U0 computes SK = H(r||y1||y2||...||y
n
||SID) and broadcasts (U0, y1, y2,..., y
n
, z0, SID) to all clients.
Step 3: Upon receiving the messages (U0, y1, y2,..., yn, z0, SID), each client U
i
(1 ≤ i ≤ n) can compute  and uses r to obtain the group key SK = H(r||y1||y2||...||y
n
||SID).
and uses r to obtain the group key SK = H(r||y1||y2||...||y
n
||SID).
Member joining phase. Assume that a new client Un+1want to join the group. This phase is depicted in Figure 2 and the detailed steps are described as follows.
Step 1: Only the client Un+1randomly selects a value  and computes
and computes  . Then, Un+1sends (Un+1, zn+1) to the powerful node U0.
. Then, Un+1sends (Un+1, zn+1) to the powerful node U0.
Step 2: Upon receiving the pair (Un+1, zn+1), the powerful node U0 computes  and selects a new value r' ∈
R
Z
q
*. Then, U0 computes
and selects a new value r' ∈
R
Z
q
*. Then, U0 computes  for i = 1, 2,..., n+1 and
for i = 1, 2,..., n+1 and  . Finally, the powerful node U0 broadcasts
. Finally, the powerful node U0 broadcasts  to all clients.
to all clients.
Step 3: Upon receiving the messages  , each client U
i
(1 ≤ i ≤ n) can compute
, each client U
i
(1 ≤ i ≤ n) can compute  and uses r' to obtain a new group key
and uses r' to obtain a new group key  The client Un+1first computes
The client Un+1first computes  and
and  to obtain the group key SK'.
to obtain the group key SK'.
Member leaving phase. Without loss generality, we assume that the client Un+1would like to leave the group. This phase is depicted in Figure 3 and the detailed steps are described as follows.
Step 1: The powerful node U0 first selects a new random value  . Then, U0 computes
. Then, U0 computes  for i = 1, 2,..., n and
for i = 1, 2,..., n and  Finally, the powerful node U0 broadcasts
Finally, the powerful node U0 broadcasts  to all other clients.
to all other clients.
Step 2: Upon receiving the message  each client U
i
(1 ≤ i ≤ n) can compute
each client U
i
(1 ≤ i ≤ n) can compute  and uses r″ to obtain a new group key
and uses r″ to obtain a new group key 
Security analysis
In this section, we demonstrate that our proposed GKE protocol can achieve the security requirements defined in 'Security requirements for dynamic GKE protocol' subsection that include withstanding passive attack, satisfying contributiveness and providing forward/backward secrecy.
Passive attacks
Theorem 1. Under the decision Diffie-Hellman assumption, the proposed group key exchange protocol is secure against passive attacks.
Proof. Assume that there exists an adversary A who tries to obtain the information about the group key by eavesdropping the transmitted messages over a public channel. Suppose that the adversary A may obtain all transmitted messages (z0, z
i
, y
i
, SID) for i = 1, 2,..., n, where  and
and  . Here, we want to prove that the adversary A cannot get any information about the group key SK = H(r||y1||y2||...||y
n
||SID). Under the decision Diffie-Hellman assumption, we prove that two tuples (z
i
, y
j
, SK = H(r||y1||y2||...||y
n
||SID)) and (z
i
, y
j
, R1) are computationally indistinguishable for 0 ≤ i ≤ n and 1 ≤ j ≤ n, where R1 ∈ G
q
.
. Here, we want to prove that the adversary A cannot get any information about the group key SK = H(r||y1||y2||...||y
n
||SID). Under the decision Diffie-Hellman assumption, we prove that two tuples (z
i
, y
j
, SK = H(r||y1||y2||...||y
n
||SID)) and (z
i
, y
j
, R1) are computationally indistinguishable for 0 ≤ i ≤ n and 1 ≤ j ≤ n, where R1 ∈ G
q
.
By contradiction proof, we assume that the adversary A within a polynomial-time can efficiently distinguish (z
i
, y
j
, SK = H(r||y1||y2||...||y
n
||SID)) and (z
i
, y
j
, R1) for 0 ≤ i ≤ n and 1 ≤ j ≤ n. Then, we can construct an algorithm A1 that can efficiently distinguish a decision Diffie-Hellman (DDH) problem (u
a
, u
b
,  ) from (u
a
, u
b
, R2), where
) from (u
a
, u
b
, R2), where  and
and  for r
a
,
for r
a
,  and R2 ∈ G
q
. Without loss generality, we set u
a
= z0 and u
b
= y1 as the inputs of the algorithm A1, A1 selects n values t1, t2,..., t
n
∈
R
Z
q
* and computes following values:
and R2 ∈ G
q
. Without loss generality, we set u
a
= z0 and u
b
= y1 as the inputs of the algorithm A1, A1 selects n values t1, t2,..., t
n
∈
R
Z
q
* and computes following values:

and

Now, the algorithm A1 has constructed all (z i , y j ) and then computes R1 = H(y1⊕H(R2||SID)||y1||y2||...||y n ||SID) for 0 ≤ i ≤ n and 1 ≤ j ≤ n. Finally, A1 sends (z i , y j , R1) to the adversary A.
The adversary A can determine whether SK is equal to R1. If it is true, then  This means that the algorithm A1 can run A as a subroutine to efficiently distinguish two tuples (u
a
, u
b
,
This means that the algorithm A1 can run A as a subroutine to efficiently distinguish two tuples (u
a
, u
b
,  ) from (u
a
, u
b
, R2). It is a contradiction for the decision Diffie-Hellman assumption. Thus, the proposed dynamic key exchange protocol is secure against passive attacks.■
) from (u
a
, u
b
, R2). It is a contradiction for the decision Diffie-Hellman assumption. Thus, the proposed dynamic key exchange protocol is secure against passive attacks.■
Contributiveness
Theorem 2. By running the proposed group key exchange protocol, an identical group key is established by the group participants. Then, each participant may ensure that her/his contribution has been involved in the group key.
Proof. In the proposed protocol, after the powerful node U0 broadcasts (U0, y1, y2,..., y n , z0, SID) to all clients, each client U i (1 ≤ i ≤ n) can use its own secret r i to compute the value r and then obtains an identical group key SK. Thus, this means that the following equations hold:

Set  . It implies
. It implies  . Obviously, each y
i
includes the participant U
i
's secret value r
i
for i = 1, 2,..., n. By the group key
. Obviously, each y
i
includes the participant U
i
's secret value r
i
for i = 1, 2,..., n. By the group key  , each participant may ensure that her/his contribution has been involved in the group key SK. Therefore, our proposed GKE protocol provides contributiveness.■
, each participant may ensure that her/his contribution has been involved in the group key SK. Therefore, our proposed GKE protocol provides contributiveness.■
For convenience to prove the forward/backward secrecy for member joining/leaving, we first prove a lemma as follow.
Lemma 3. Assume that three secret parameters a, b, and c are randomly selected from Z p *. If a passive adversary knows two values H(a)⊕b and H(a)⊕c, then the secret b is un-computable under the hash function assumption. Furthermore, the secret a is also un-computable under the same assumption.
Proof. Note that if the passive adversary can get the secret b from U = H(a)⊕b and V = H(a)⊕c, then it implies that the adversary can obtain H(a) from U and V. In the following, we want to prove that the passive adversary is unable to get H(a) from U and V under the hash function assumption.
By the contradiction proof, assume that there exists an algorithm A can obtain the value H(a) from H(a)⊕b and H(a)⊕c within a polynomial-time. If the algorithm A cannot get a, then it is hard to find x = a such that H(x) = H(a) and x ≠ a such that H(x) = H(a) by the hash function assumption (ii). Thus, the algorithm A must get a. That is, there exists an algorithm A which is able to obtain the secret a from H(a)⊕b and H(a)⊕c within the polynomial-time.
Based on the algorithm A, we can construct another algorithm A1 which is able to get x from H(x) within the polynomial-time as follows. Set the value H(x) as input of the algorithm A1. A1 executes the following procedures to obtain x:
-
(1)
The algorithm A1 calls the algorithm A with the input H(x)⊕R, where R is a nonce.
-
(2)
The algorithm A1 can obtain x from the algorithm A.
According to the above procedures, the algorithm A1 can get x from H(x) within the polynomial-time. This is a contradiction for the one-way property of the hash function assumption. Therefore, no passive adversary can compute the secret b from H(a)⊕b and H(a)⊕c under the hash function assumption. Certainly, the secret a is also un-computable under the same assumption.■
Forward secrecy
Theorem 4. Under the computation Diffie-Hellman (CDH) and the hash function assumptions, the proposed group key exchange protocol provides forward secrecy for member joining.
Proof. Assume that a new client Un+1would like to join the group. According to the proposed protocol, Un+1sends  to the powerful node U0. Then, U0 selects
to the powerful node U0. Then, U0 selects  and computes
and computes  with a new SID'. Finally, U0 broadcasts
with a new SID'. Finally, U0 broadcasts  to all other clients. Hence, all participants can compute a new group key
to all other clients. Hence, all participants can compute a new group key  , where
, where  .
.
Here, we want to prove that the client Un+1cannot compute the previous group key SK = H(r||y1||...||y
n
||SID). We may assume that Un+1has recorded the previous transmitted messages  for i = 1, 2,..., n. Obviously, if Un+1can get the value r or x
i
for some i ∈ {1, 2,..., n}, then the key SK can be computed. Hence, we want to prove that the following two cases do not occur.
for i = 1, 2,..., n. Obviously, if Un+1can get the value r or x
i
for some i ∈ {1, 2,..., n}, then the key SK can be computed. Hence, we want to prove that the following two cases do not occur.
Case I. Un+1can obtain x
i
from z
i
(0 ≤ i ≤ n). Due to  , given a tuple
, given a tuple  , it is hard to compute
, it is hard to compute  , by the computational Diffie-Hellman (CDH) assumption. Thus, Un+1obtaining x
i
from z
i
is impossible.
, by the computational Diffie-Hellman (CDH) assumption. Thus, Un+1obtaining x
i
from z
i
is impossible.
Case II. Un+1can get the value r or x
i
from (y
i
,  , SID, SID') for i = 1, 2,..., n, where
, SID, SID') for i = 1, 2,..., n, where  and
and  . Without loss generality, we set a = x
i
||SID = x
i
||SID', b = r, and c = r' such that y
i
= H(a)⊕b and
. Without loss generality, we set a = x
i
||SID = x
i
||SID', b = r, and c = r' such that y
i
= H(a)⊕b and  . By Lemma 3, we have proven that the values a and b are un-computable under the hash function assumption. Thus, to obtain the value r or x
i
is also impossible.
. By Lemma 3, we have proven that the values a and b are un-computable under the hash function assumption. Thus, to obtain the value r or x
i
is also impossible.
Therefore, the client Un+1cannot compute the previous group key SK by Cases I and II. This means that the proposed group key exchange protocol provides forward secrecy.■
Backward secrecy
Theorem 5. Under the computation Diffie-Hellman (CDH) and the hash function assumptions, the proposed dynamic group key exchange protocol provides backward secrecy for member leaving.
Proof. Without loss generality, we assume that an old client Un+1wants to leave the group. According to the proposed protocol, the powerful node U0 selects a new random value  and computes
and computes  with a new SID". Then, U0 broadcasts
with a new SID". Then, U0 broadcasts  to all other participants. Hence, all participants can compute a new group key
to all other participants. Hence, all participants can compute a new group key 
Here, we prove that the client Un+1cannot compute the later group key  We may assume that Un+1has recorded all transmitted messages
We may assume that Un+1has recorded all transmitted messages  for i = 1, 2,..., n, where
for i = 1, 2,..., n, where  . Due to the key
. Due to the key  and
and  , if Un+1can get the value r″ or x
i
for some i ∈ {1, 2,..., n} then SK″ can be computed. However, Un+1cannot obtain the values r″ and x
i
from
, if Un+1can get the value r″ or x
i
for some i ∈ {1, 2,..., n} then SK″ can be computed. However, Un+1cannot obtain the values r″ and x
i
from  by the similar method in the proof of Theorem 4. Thus, the client Un+1cannot compute the later group key SK″. Finally, the proposed group key exchange protocol provides backward secrecy.■
by the similar method in the proof of Theorem 4. Thus, the client Un+1cannot compute the later group key SK″. Finally, the proposed group key exchange protocol provides backward secrecy.■
Performance analysis and discussions
For convenience to analyze the performance of our proposed dynamic GKE protocol, we first define the following notations:
-
Texp: The time of executing a modular exponentiation operation.
-
Tinv: The time of executing a modular inverse operation.
-
Tmul: The time of executing a modular multiplication operation.
-
T H : The time of executing a one-way hash function operation.
-
|m|: the bit length of a transmitted message m.
Here, let us discuss the computational cost for each client U i (1 ≤ i ≤ n). In Step 1, the client U i computes z i , thus it requires Texp. Upon receiving (U0, y1, y2,..., y n , z0, SID), the client U i computes r and then uses r to obtain the group key SK, thus Texp+2T H is required in Step 3. The required computational cost for each client U i is 2Texp + 2T H . Considering the computational cost of the powerful node, the powerful node might be regarded as a wired gateway with less computing-restriction. In Step 2 of the proposed protocol, the powerful node U0 computes z0, x i and y i for i = 1, 2,..., n. Then the powerful node U0 computes SK. In total, it requires (n + 1)Texp + (n + 1)T H . Furthermore, let us discuss the computation cost required for member joining/leaving. The powerful node's computation cost for joining and leaving requires Texp + (n + 2)T H and (n + 1)T H , respectively. Each client's computation costs for joining/leaving requires 2T H , except for the joining client.
In Table 1, we demonstrate the comparisons between our GKE protocol and the recently proposed GKE protocols [20, 22] in terms of the number of rounds, the computational cost and the communication complexity required for each client, the powerful node, and the dynamic member joining/leaving, respectively. It is easy to see that the performance of our GKE protocol is better than Nam et al.'s [20] and the Chuang-Tseng [22] GKE protocols. Meanwhile, our GKE protocol also provides the member dynamic joining/leaving functionality and satisfies contributiveness.
Since Nam et al.'s protocol [20], the Chuang-Tseng protocol [22], and our proposed protocol are non-authenticated GKE ones, they must rely on an authenticated channel or apply other schemes to provide authentication like the Katz-Yung complier [12]. Using their complier into a non-authenticated GKE protocol, the protocol can be transformed into an authenticated GKE. Nevertheless, it will additionally increase a new round, one signature generation, and n - 1 signature verifications for each client. Thus, the computational cost is too expensive for each mobile client. The other option is that each client needs not to authenticate the other clients. It only authenticates the powerful node. Certainly, the powerful node must be trusted. Then, it requires single signature generation and verification for each client. Naturally, the powerful server will additionally add one signature generation and n - 1 signature verifications. Fortunately, some known wireless network environment such as cellular mobile networks [3] and wireless local area networks [1], these clients must be authenticated before they want to connect to their network systems. In addition, the powerful node may apply some existing authentication protocols [23–25] to authenticate the mobile client in advance.
Conclusions
In this article, we have proposed a new dynamic GKE protocol for wireless network environments. Under the decision Diffie-Hellman (DDH), the computation Diffie-Hellman (CDH), and the hash function assumptions, we have proven that the proposed protocol is secure against passive attacks and provides forward/backward secrecy for member joining/leaving. Meanwhile, we have proven that the proposed protocol satisfies contributiveness. As compared with the recently presented GKE protocols, we have demonstrated that our protocol provides better performance in terms of computational cost, round number, and communication cost.
Abbreviations
- CDH:
-
computation Diffie-Hellman
- DDH:
-
decision Diffie-Hellman
- GKE:
-
group key exchange
- PDA:
-
personal digital assistant.
References
ANSI/IEEE. Wireless LAN media access control (MAC) and physical layer (PHY) specifications. ANSI/IEEE Std 1999 802.11: 1999 (E) Part 11, ISO/IEC8802-11
Perkins C: Ad Hoc Networking. Addison-Wesley, MA; 2001.
GPRS: General packet radio services (GPRS) service description (stage 2). 2002.
Akyildiz I, Su W, Sankarasubramaniam Y, Cayirci E: A survey on sensor networks. IEEE Commun, Mag 2002, 40(8):102-114. 10.1109/MCOM.2002.1024422
Phan T, Huang L, Dulan C: Challenge: integrating mobile wireless devices into the computational grid. Proceedings of MOBICOM' 02 2002, 271-278.
Yang H, Luo H, Ye F, Lu S, Zhang L: Security in mobile ad hoc networks: challenges and solutions. IEEE Wireless Commun 2004, 11(1):38-47. 10.1109/MWC.2004.1269716
Ingemaresson I, Tang TD, Wong CK: A conference key distribution system. IEEE Trans Inform Theory 1982, 28(5):714-720. 10.1109/TIT.1982.1056542
Diffie W, Hellman ME: New directions in cryptography. IEEE Trans. Inform. Theory 1976, 22(6):644-654.
Bresson E, Manulis M: Contributory group key exchange in the presence of malicious participants. IET Inform Security 2008, 2(3):85-93. 10.1049/iet-ifs:20070113
Burmester M, Desmedt Y: A secure and efficient conference key distribution system.Inform. Process. Lett 2005, 94(3):137-143.
Katz J, Shin JS: Modeling insider attacks on group key exchange protocols. Proceedings of CCS' 05 2005, 180-189.
Katz J, Yung M: Scalable protocols for authenticated group key exchange. J Crypt 2007, 20: 85-113. 10.1007/s00145-006-0361-5
Tseng YM: A robust multi-party key agreement protocol resistant to malicious participants. Comput J 2005, 48(4):480-487. 10.1093/comjnl/bxh111
Ateniese G, Steiner M, Tsudik G: New multiparty authentication services and key agreement protocols. IEEE J Select Areas Commun 2000, 18(4):628-639. 10.1109/49.839937
Bresson E, Chevassut O, Pointcheval D: Dynamic group Diffie-Hellman key exchange under standard assumptions. Proceedings of EUROCRYPT' 02 2002, 321-336. LNCS 2332
Steiner M, Tsudik G, Waidner M: Diffie-Hellman key distribution extended to group communication. Proceedings of CCS' 96 1996, 31-37.
Steiner M, Tsudik G, Waidner M: Key agreement in dynamic peer groups. IEEE Trans. Parallel Distribut. Syst 2000, 11(8):769-780.
Boyd C, Nieto G: Round-optimal contributory conference key agreement. Proceedings of PKC' 03 2003, 161-174. LNCS 2567
Bresson E, Chevassut O, Essiari A, Pointcheval D: Multual authentication and group key agreement for low-power mobile devices. Comput. Commun 2004, 27(7):1730-1737.
Nam J, Lee J, Kim S, Won D: DDH-based group key agreement in a mobile environment. J Syst Softw 2005, 78(1):73-83.
Tseng YM: A resource-constrained group key agreement protocol for imbalanced wireless networks. Comput Security 2007, 26(4):331-337. 10.1016/j.cose.2006.12.001
Chuang YH, Tseng YM: An efficient dynamic group key agreement protocol for imbalanced wireless networks. Int J Netw Manage 2010, 20(4):167-180.
Arkko J, Haverinen H: EAP AKA authentication. Draft-Arkko-Pppext-Eap-Aka-11, IETF 2003.
Tseng YM: GPRS/UMTS-aided authentication protocol for wireless LANs. IEE Proc Commun 2006, 153(6):810-817. 10.1049/ip-com:20050366
Tseng YM: USIM-based EAP-TLS authentication protocol for wireless local area networks. Comput Stand Interfaces 2009, 31(1):128-136. 10.1016/j.csi.2007.11.014
Boneh D: The decision Diffie-Hellman problem. Proceedings of 3rd Algorithmic Number Theory Symposium 1998, 48-63.
Shoup V: Lower bounds for discrete logarithms and related problems. Proceedings of Advances in Cryptology - Eurocrypt' 97 1997, 256-266.
NIST/NSA FIPS 180-2: Secure Hash Standard (SHS). NIST/NSA, Gaithersburg, MD; 2005.
Acknowledgements
This research was partially supported by National Science Council, Taiwan, ROC, under contract no. NSC97-2221-E-018-010-MY3.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, TY., Tseng, YM. & Yu, CW. Two-round contributory group key exchange protocol for wireless network environments. J Wireless Com Network 2011, 12 (2011). https://doi.org/10.1186/1687-1499-2011-12
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1499-2011-12





 and
and 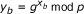 for some x
a
, x
b
∈ Z
q
*, the DDH problem is to distinguish two tuples (y
a
, y
b
,
for some x
a
, x
b
∈ Z
q
*, the DDH problem is to distinguish two tuples (y
a
, y
b
,  ) and (y
a
, y
b
, R ∈ G
q
).
) and (y
a
, y
b
, R ∈ G
q
).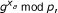
 ) for some x
a
, x
b
∈ Z
q
*, the CDH problem is to compute the value
) for some x
a
, x
b
∈ Z
q
*, the CDH problem is to compute the value 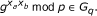
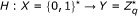 must satisfy following requirements [
must satisfy following requirements [

