Abstract
Background
Understanding the evolutionary relationships among species based on their genetic information is one of the primary objectives in phylogenetic analysis. Reconstructing phylogenies for large data sets is still a challenging task in Bioinformatics.
Results
We propose a new distance-based clustering method, the shortest triplet clustering algorithm (STC), to reconstruct phylogenies. The main idea is the introduction of a natural definition of so-called k-representative sets. Based on k-representative sets, shortest triplets are reconstructed and serve as building blocks for the STC algorithm to agglomerate sequences for tree reconstruction in O(n2) time for n sequences.
Simulations show that STC gives better topological accuracy than other tested methods that also build a first starting tree. STC appears as a very good method to start the tree reconstruction. However, all tested methods give similar results if balanced nearest neighbor interchange (BNNI) is applied as a post-processing step. BNNI leads to an improvement in all instances. The program is available at http://www.bi.uni-duesseldorf.de/software/stc/.
Conclusion
The results demonstrate that the new approach efficiently reconstructs phylogenies for large data sets. We found that BNNI boosts the topological accuracy of all methods including STC, therefore, one should use BNNI as a post-processing step to get better topological accuracy.
Similar content being viewed by others
Background
Reconstructing the evolutionary relationships among species based on their genetic information is one of the primary objectives in phylogenetic analysis. In recent years, numerous heuristics to reconstruct phylogenies for large data sets have been proposed [1–11]. In addition, parallel tree-reconstruction programs have been implemented [12–15].
To date, distance-based methods introduced by Cavalli-Sforza and Edwards [16] and by Fitch and Margoliash [17] appear most appropriate to reconstruct phylogenies based on thousands of sequences. These methods are a compromise between computational speed and topological accuracy [1, 3, 5–7] and run typically in O(n3) time for n sequences [1, 3, 5] or in O(n2) for recently suggested approaches [6, 7]. Clustering algorithms form a major class of distance-based methods [18]. They do not have an explicit objective function that needs to be optimized. They rather group sequences (or taxa) iteratively to reconstruct a distance-based phylogenetic tree. UPGMA is a popular method to infer phylogenies with the constraint that a molecular clock is imposed on the evolutionary process. Other clustering approaches have been proposed to relax the molecular clock assumption [1, 3, 5, 19–21].
An attempt to boost the accuracy and to reduce the computational burden is the introduction of k-representative set concepts [10, 11]. k- representative sets consist of at most k elements but retain the most important information from whole sets. In this paper, we extend our original approach [10] by introducing a more natural k- representative set concept. In a nutshell, representative sets are regarded as components to construct shortest triplets, each of which comprises three closely related sequences from three k-representative sets. The collection of shortest triplets serves as building block for a new distance-based clustering method called shortest triplet clustering algorithm (STC).
Results
Simulations were run on a PC cluster with 16 nodes. Each node has two 1.8 GHz processors and 2 GB RAM. Seq-Gen [22] was used to evolve sequences along trees using the Kimura two-parameter model [23] with a transition/transversion ratio of 2.0. We generated 100 simulated data sets of 500 sequences each with sequence lengths 500, 1000 and 2000 nucleotides (nt), respectively. As one model tree, we used the rbcl gene tree with diameter 0.36 substitutions per site as inferred from an alignment of 500 rbcl-genes [10]. We call this the rbcl-simulation.
In a second experiment, the so-called large simulation, tree topologies were drawn from the Yule-Harding distribution [24], and edge lengths were drawn from an exponential distribution and subsequently rescaled such that the mean diameter of the tree was either 0.1, 0.5, 1.0, or 1.5. For each value of the diameter we generated 100 trees with 1000 sequences and 100 trees with 5000 sequences. Thus, a total of 800 trees were used.
Finally, we tested the accuracy and runtime of the STC and compared it with six other commonly used distance-based methods. More specifically, we investigate the performance of the Neighbor-Joining method (NJ) [1] implemented in PAUP* 4.0 [25], BIONJ [3], Weighbor 1.2 [5], Harmony Greedy Triplet and Four Point Condition (HGT/FP) [7] as well as Greedy Minimum Evolution (GME) and Balanced Minimum Evolution (BME) [6]. Unfortunately, no distance-based program is available for the disc-covering method [4]. All methods were combined with DNADIST version 3.5 [26] and pairwise distances were corrected for multiple hits according to the model used in the simulation. Moreover, we examined the performance of all methods when the balanced nearest neighbor interchange (BNNI) [6] is used as a post-processing step.
Further, to illustrate the performance of STC we re-analyzed the 96-taxon alignments of sequence length 500 nt, that were analyzed in [6] and available at http://www.lirmm.fr/~guindon/simul/. The 6000 trees were split into three groups called "slow" (0.2 substitutions per site), "moderate" (0.4 substitutions per site) and "fast" (1.0 substitutions per site). We call this the re-analyzed simulation.
The accuracy of a tree reconstruction method for a simulated data set is measured by the Robinson and Foulds (RF) distance [27] between the inferred tree and the model tree used to generate the data set. The RF distance between two trees is the number of bi-partitions present in one of the two trees but not the other, divided by the number of possible bi-partitions. Thus, the smaller the RF distance between two trees the closer are their topologies. In other words, the smaller the RF distance is between the inferred tree and the model tree the higher is the topological accuracy of the tree reconstruction method.
In the following we discuss the results of the rbcl-simulation, and the large simulation and the re-analyzed simulation.
rbcl-simulation
Table 1 shows that the STC outperforms all other methods analyzed in terms of topologlcal accuracy. For instance, the RF distance between the STC-tree and the model tree is on average 0.177 (with respect to the sequence length of 500 nt) and better than NJ (0.190), slightly better than the second best method BME (0.184) and much better than HGT/FP (0.512). Table 1 also demonstrates that all tested methods including STC give higher topologlcal accuracy when the sequence length is increased. However, Table 2 shows that other methods in combination with BNNI outperform STC without BNNI. The combination of STC and BNNI shows similar performance as the combinations of NJ (BIONJ, Weighbor) and BNNI and, slightly better results than the combination of GME (HGT/FP) and BNNI.
Large simulation
Due to the increase in runtime, Weighbor could not be tested. Table 3 and 4 show that STC gives better results than the other methods independent of the diameter. All methods display a decrease in accuracy when the number of sequences changes from 1000 to 5000. As shown in Table 5 and 6, BNNI boosts the accuracy of all methods including STC. All methods give similar results when being used together with BNNI.
Re-analyzed simulation
Except for STC, the accuracies for the other methods displayed in Table 7 and 8 were taken from [6]. Table 7 shows that STC outperforms the other methods in terms of topological accuracy with the exception that Weighbor is slightly better than STC with respect to the slow simulation group. If BNNI is applied, all methods exhibit an almost identical performance (see Table 8).
Another look at the performance
Instead of looking at the average RF distance, we suggest to take a closer look at the simulated data. For each simulated data set, that is subjected to the STC and six other tree reconstruction methods mentioned above, we compute the RF distance between the reconstructed tree and the model tree for all methods. Figure 1 illustrates the results for the large simulation when comparing STC with NJ (left column) and STC with the second best method BME (right column). In each diagram specified by the number of taxa and reconstruction methods, 400 points are displayed, that resulted from 100 simulations for each of the tree-diameters (0.1, 0.5, 1.0 and 1.5). Although four tree-diameters were studied only two clouds of points are discernible, where the cloud in the north-east corner of each diagram represents the simulations with the tree-diameter 0.1. The remaining 300 points gather in the south-west cloud because the RF-distances from trees with diameter 0.5, 1.0, 1.5 are not substantially different from each other (see Table 3 and 4). More precisely, the horizontal and vertical axes indicate the RF distances of STC and NJ (or BME), respectively. Each point in the graph presents the RF distance for a simulated data set. Points above the dotted line are examples where the RF distance of the STC-tree is less than the RF distance of the NJ-tree or BME-tree. Thus, the STC gives higher topological accuracy than NJ or BME with respect to the simulated data set. For example, Figure 1a illustrates the comparison between STC and NJ with respect to 1000 taxa data sets. 379 out of 400 points are above the diagonal, thus, STC gives better results than NJ in about 95% of the simulations. For the remaining 21 alignments (points), two methods showed the same RF distance. Finally, we found 19 points below the diagonal in which case NJ outperforms STC. For the large simulation (5000 taxa), NJ is worse than STC in all cases. However, the second best method BME is better than STC in 11% and 5% of the cases with respect to 1000 and 5000 sequence data sets.
The comparisons of topological accuracy between STC, NJ and BME for the large simulation. Each point in the graph presents the Robinson and Foulds (RF) distance for a simulated data set. Points above the dotted line are examples where the RF distance of the STC-tree is less than the RF distance of the NJ-tree or BME-tree. Thus, the STC gives higher topological accuracy than NJ or BME with respect to the simulated data set.
Figure 2 shows the same analysis for the rbcl simulation. It shows that with increasing sequence length the cloud of points moves towards zero. From Figure 2 we learn that in some instances NJ (or BME) performs better (with regard to the RF distance) than STC, i.e. 20%, 12%, 8% (or 34%, 17%, 14%) of the simulations for sequence lengths 500, 1000 and 2000 nt, respectively.
The comparisons of topological accuracy between STC, NJ and BME for the rbcl simulation. Each point in the graph presents the Robinson and Foulds (RF) distance for a simulated data set. Points above the dotted line are examples where the RF distance of the STC-tree is less than the RF distance of the NJ-tree or BME-tree. Thus, the STC gives higher topological accuracy than NJ or BME with respect to the simulated data set.
Similar results hold for the other methods. These results are summarized in Table 9 where we show the percentage of simulations in which STC is at least as good as the other methods.
Again, if BNNI is applied we observe that no substantial difference among the various approaches. The accuracy of the methods is mostly determined by BNNI (see Table 10).
Conclusion
We are presenting k-representative sets which allow us to design a fast and accurate method to reconstruct phylogenies from large data sets with 1000 or more taxa. Simulations show that STC gives better results than other tested methods in terms of topological accuracy. However, if BNNI is introduced as a subsequent optimization step, the differences in the performance disappear. All methods show more or less the same accuracy. Thus, one should apply BNNI to improve the topological accuracy.
The time to reconstruct a tree of up to 1000 sequences is not really an issue for all tested distance-based methods, with the exception of Weighbor. Weighbor needed about 19 minutes to reconstruct a tree with 500 sequences, thus it is only applicable to data sets with up to some hundred sequences. For data sets with up to 1000 sequences, the remaining methods needed less than one minute to output a tree, thus the difference between methods in terms of runtime is not significant. For data sets with 5000 sequences, STC (GME, HGT/FP or BME) with BNNI took about 2.0 (2.5, 3.0 or 3.5) minutes to reconstruct a tree. NJ (BIONJ) with BNNI were slower and consumed approximately six minutes to output a tree. In short, the combination of STC and BNNI efficiently reconstruct trees for large data sets in both terms of topological accuracy and runtime.
Finally, we did not systematically evaluate the impact of the number of representatives k. We present some preliminary results for k = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90 and 100. Figure 3 shows that the RF distance of STC decreases when k grows from 1 to 5. This proves our intuition that a too small number of triplets leads to an inaccurate estimate of path lengths and edge lengths. When k ranges from 5 to 10, the RF distance remains more or less unchanged. For k ≥ 10, the RF distance increases steadily indicating a loss of accuracy. The decrease in accuracy is explained by the inclusion of triplets with large distances which include noise and disturb the reconstruction. Thus, we chose k = 5 as a good compromise between the accuracy and computational complexity for all data sets. That is, the practical complexity of the STC algorithm is only O(n2).
Methods
In this section we introduce a new clustering algorithm to reconstruct phylogenies based on distance matrices.
Additive distances
Let S = {s1, s2,..., s n } be a set of n objects (typically contemporary sequences/taxa), let D = D(uv) be a distance matrix where D(uv) is the distance between two objects u and v.
Definition 1
The distance matrix D is additive if and only if it satisfies the four-point condition [28]: for any quartet {u, v, w, x},
D(uv) + D(wx) ≤ max{D(uw) + D(vx), D(ux) + D(vw)}.
In this case, the objects s ∈ S are related by a tree T = (V, E) where V is the set of vertices such that S ⊂ V and E = {{v1, v2}|v1, v2 ∈ V} is the set of edges. A vertex with one adjacent edge is called a leaf, all other vertices are called internal nodes. We let L ⊂ V be the leaf set of the tree T. Note that we typically require L ⊆ S in the phylogenetic setting.
If D is additive, then there exists a map  and a length function
and a length function  such that
such that

for all u, v ∈ S where p(φ (u), φ(v)) is the unique path connecting φ(u) and φ(v) in T and  denotes the distances between vertices in T (cf. [29]). ℓ(e) is called edge length of the edge e. To avoid unnecessary complication, we consider only one-to-one maps from S on the leaf set L of T. If D is additive, the reconstruction of tree T and ℓ is trivial. If D is not additive, methods are available that try to fit a tree T to D with respect to an objective function (cf. [30]). Thus, in the following we consider arbitrary distance matrices and we want to reconstruct a tree
denotes the distances between vertices in T (cf. [29]). ℓ(e) is called edge length of the edge e. To avoid unnecessary complication, we consider only one-to-one maps from S on the leaf set L of T. If D is additive, the reconstruction of tree T and ℓ is trivial. If D is not additive, methods are available that try to fit a tree T to D with respect to an objective function (cf. [30]). Thus, in the following we consider arbitrary distance matrices and we want to reconstruct a tree  together with a length function
together with a length function  .
.
Estimating edge lengths using triplets
We consider a subset X of S, then  induces a map on a subtree of T such that the relationships of objects in X are displayed by the subtree with leaf set φ(X). The complement S0(X) = S - X we will call the unclassified object set, because the relationships of objects in S0(X) to X is not known from the subtree. Note that we will use S0 instead of S0(X) if X is clear from the context.
induces a map on a subtree of T such that the relationships of objects in X are displayed by the subtree with leaf set φ(X). The complement S0(X) = S - X we will call the unclassified object set, because the relationships of objects in S0(X) to X is not known from the subtree. Note that we will use S0 instead of S0(X) if X is clear from the context.
Let denote T r = (V r , E r ) a rooted tree with root r and leaf set L r , and let S r be a subset of S such that φ(S r ) = L r . For convenience, we use S r and L r interchangeably.
Now, we consider the most simple edge length estimation problem. That is, we would like to estimate the edge lengths for a triplet tree {a, b, c} with distance matrix D (see Figure 4a). Edge lengths are estimated as follows



Now consider a rooted T
r
with the inferred tree-like metric  . The rooted tree T
r
consists of two rooted subtrees
. The rooted tree T
r
consists of two rooted subtrees  and
and  (see Figure 4b). For convenience, we will use T
i
instead of
(see Figure 4b). For convenience, we will use T
i
instead of  if r
i
is clear from the context. The leaf set S
r
= {S1 ∪ S2} where S
r
⊂ S and S0 = S - S
r
is not represented in T
r
. Then we can compute
if r
i
is clear from the context. The leaf set S
r
= {S1 ∪ S2} where S
r
⊂ S and S0 = S - S
r
is not represented in T
r
. Then we can compute



for each triplet (s0, s1, s2) ∈ (S0 × S1 × S2).
With

(s1r1) and  (s2r2) we denote the known distances of s1 and s2 to their roots r1 and r2. Thus, we can compute for each triplet {s0, s1, s2} the lengths ℓ(r1r) and ℓ(r2r) as
(s2r2) we denote the known distances of s1 and s2 to their roots r1 and r2. Thus, we can compute for each triplet {s0, s1, s2} the lengths ℓ(r1r) and ℓ(r2r) as


Note that, if D is additive and T1, T2 are isometric subtrees of T, the lengths ℓ(r1r) and ℓ(r2r) do not depend on the choice of the triplet {s0, s1, s2}.
Regardless of additivity considerations, we may define the average length for a fixed s0 ∈ S0 as

We can estimate edge lengths ℓ(r1r) and ℓ(r2r) by using all possible triplets as


Recovering a tree from a distance matrix
The largest path length criterion
We want to reconstruct a tree T = (V, E) with respect to a distance matrix D such that D T represents D. To this end, we use triplets and the notation of a rooted tree T r together with Equations 4 and 5.
Our algorithm starts with the observation that if we take an arbitrarily rooted tree T
m
with m ∈ S and length function  , then there must be a pair of leaves (neighboring leaves) that share an immediate most recent common ancestor mrca which is farthest away from the root m with respect to
, then there must be a pair of leaves (neighboring leaves) that share an immediate most recent common ancestor mrca which is farthest away from the root m with respect to  . In Figure 5, the pair (3, 4) satisfies this condition, we say this pair fulfills the largest path length criterion. The largest path length criterion easily generalizes to arbitrarily rooted subtrees T
i
and T
j
of T
m
, where all descendants from the roots of T
i
and T
j
are in the vertex sets V
i
or V
j
, respectively.
. In Figure 5, the pair (3, 4) satisfies this condition, we say this pair fulfills the largest path length criterion. The largest path length criterion easily generalizes to arbitrarily rooted subtrees T
i
and T
j
of T
m
, where all descendants from the roots of T
i
and T
j
are in the vertex sets V
i
or V
j
, respectively.
Let
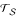
be the set of rooted subtrees of T m (each leaf l ∈ L m is considered as a rooted subtree T l ). Now consider two disjoint rooted subtrees T i and T j of T m where i, j ∈ V m . Then the distance ℓ(m, mrca|m S i S j ) from the mrca of T i and T j to m is computed according to Equation 4, where S i and S j are the leaf sets of T i and T j , respectively. Then we pick
(

,  ) = argmax{ℓ(m, mrca|m S
i
S
j
) | T
i
, T
j
∈
) = argmax{ℓ(m, mrca|m S
i
S
j
) | T
i
, T
j
∈ 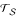 } (6)
} (6)
as a pair of neighbors (if we detect more than one pair, we randomly select one). By construction, (

,  ) fulfills the largest path length criterion.
) fulfills the largest path length criterion.
If D is additive, ℓ(m, mrca|mS
i
S
j
) is exactly the path length from the mrca of (T
i
, T
j
) to m. In other words, the path length from the mrca of ( ,
,  ) to m is large stand (
) to m is large stand ( ,
,  ) is a true neighboring pair. However, in real applications D is rarely additive, therefore the root m is selected so as to avoid noise from stochastic errors involved with large distance estimates [17]. To this end, m is selected such that the distance from the farthest object to root m is minimal,
) is a true neighboring pair. However, in real applications D is rarely additive, therefore the root m is selected so as to avoid noise from stochastic errors involved with large distance estimates [17]. To this end, m is selected such that the distance from the farthest object to root m is minimal,
med = argminm'∈S{max{D(m'x)|x = 1,..., n}} (7)
med is called a median object.
Moreover, to reduce the computational complexity of finding a pair of neighbors (

,  ) using Equation 6, we store for each T
i
∈
) using Equation 6, we store for each T
i
∈ 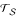 its potential neighbor Ti'∈
its potential neighbor Ti'∈ 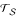 such that
such that
Ti'= argmax{ℓ(med, mrca|med, S
i
, S
j
)|T
j
∈ 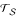 }. (8)
}. (8)
Now the neighboring pair (

,  ) fulfilling the largest path length criterion is determined as follows
) fulfilling the largest path length criterion is determined as follows
(

,  ) = argmax{ℓ(med, mrca|med, S
i
, Si')|T
i
∈
) = argmax{ℓ(med, mrca|med, S
i
, Si')|T
i
∈ 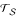 }. (9)
}. (9)
In the following, we present a natural clustering algorithm to reconstruct trees based on distance matrices and the largest path length criterion
Clustering Algorithm
-
Initial step: Find the median object med using Equation 7. Set
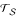 = {T1,..., T
n
} - {T
med
}. Find for each T
i
∈
= {T1,..., T
n
} - {T
med
}. Find for each T
i
∈ 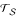 its potential neighbor Ti'∈
its potential neighbor Ti'∈ 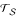 using Equation 8.
using Equation 8. -
Selection step (largest path length criterion): Find the neighboring pair (
 ,
,  ) using Equation 9.
) using Equation 9. -
Agglomeration step: Combine
 and
and  into a new rooted tree
into a new rooted tree 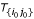 with root i0j0, and estimate new edge lengths of
with root i0j0, and estimate new edge lengths of 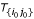 using Equation 5. Delete
using Equation 5. Delete  and
and  and add
and add 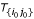 to
to 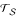 . Find the potential neighbor for the new rooted tree
. Find the potential neighbor for the new rooted tree 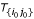 . using Equation 8, and replace Ti'for each T
i
∈
. using Equation 8, and replace Ti'for each T
i
∈ 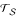 by
by 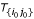 if
if 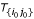 is its potential neighbor.
is its potential neighbor. -
Stopping step: If |
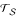 | > 1 goto the Selection step, otherwise output the tree.
| > 1 goto the Selection step, otherwise output the tree.
This algorithm is similar to approaches described elsewhere [19–21], however, an essential difference is that we estimate path lengths and edge lengths by using triplets.
Local rearrangement
The heart of the clustering algorithm is the largest path length criterion, at which the path length from the mrca of (T i , T j ) to med is estimated by ℓ(med, mrca|med, S i , S j ) using Equation 4. Thus, as path length we take the average of the lengths obtained from at most O(n2 triplets {med, s i , s j } ∈ med × S i × S j . This average may not be the representative estimate of the true path length. Moreover the root med may be too far way from the mrca and this leads to an inaccurate estimate of the path length.
To take these problems into account, we extend the clustering algorithm. To this end, imagine the algorithm has clustered T i and T j with corresponding disjoint leaf sets S i , S j ⊂ S (we have finished the agglomeration step). Thus, we have created the newly rooted tree T{ij}with leaf set S ij = {S i ∪ S j } and the set of unclassified objects S0(S ij ) = S - S ij . In the following, we describe the nearest neighbor interchange operation around the root of T i upon condition that T i consists of two rooted subtrees T x , T y (Figure 6a). First, we estimate average path lengths from the unclassified object set S0(S ij ) to the mrca of (T x , T y ), (T x , T j ) and (T y , T j ) as
Reconstruction of new rooted tree T{ij}using the the preorder traversal procedure based on the largest average path length criterion. If (T x , T y ) is the neighboring pair, we stick to the suggested grouping of T i and T j (see Figure 6a). Otherwise, if (T x , T j ) or (T y , T j ) is the neighboring pair, we switch to the trees displayed in Figure 6b or 6c, respectively.



For convenience, we will use ℓ(S0(S ij )|S x S y ) instead of ℓ(S0(S ij )S x S y |S x S y ). We now use the average path lengths from Equation 10 to decide which pair of subtrees among (T x , T y ), (T x , T j ) and (T y , T j ) is preferred. More specifically, if
ℓ(S0(S ij )|S x S y ) ≥ max{ℓ(S0(S ij )|S x S j ), ℓ(S0(S ij )|S y S j )}
we stick to the suggested grouping of T x and T y (see Figure 6a). Otherwise, if ℓ(S0(S ij )|S x S j ) or ℓ(S0(S ij )|S y S j ) is larger than the remaining average path lengths, we swap T y and T j or T x and T j as displayed in Figure 6b or 6c, respectively. Note that, this decision can be considered as a correction of the largest path length criterion by taking all possible triplets into account. We call the correction the largest average path length criterion.
We now explain the preorder traversal procedure [31] to reconstruct the rooted tree T i using the nearest neighbor interchange operation based on the largest average path length criterion (T i is a subtree of T{ij}= (T i , T j )):
Preorder traversal procedure (T i )
-
Step 1: If T i is a single leaf, return.
-
Step 2: Otherwise, T i consists of two subtrees T x and T y . Do the nearest neighbor interchange operation around the root of T i based on the largest average path length criterion (Equation 10). If T x and T j (or T y and T j ) were exchanged, estimate new edge lengths using Equation 5.
-
Step 3: Apply the preorder traversal procedure to two rooted subtrees of T i .
Representative sets and shortest triplets
For a set S of sequences (or taxa), the (genetic) distance matrix D is typically not additive due to stochastic errors [17]. Larger distances between two sequences are less accurately estimated. This leads to a low performance of both the clustering algorithm and the preorder traversal procedure for divergent data sets.
In earlier work [10, 11], we have presented simple representative concepts to reduce stochastic error involved in large distances. Here, we extend our work by introducing the so-called k-representative set concept. We use now genetic distances instead of topological distances (all edges have length 1). Our motivation is to reduce the computational complexity and to exclude objects far away from the root under consideration. In the clustering algorithm, the path length from the mrca of (T i , T j ) to med (see Figure 7) can be estimated by two approaches. The first method picks randomly one pair (s i , s j ) ∈ S i × S j then computes

The second approach takes the average distance

Both approaches suffer from noise. Estimating the path length using Equation 11 may be inaccurate because it randomly picks a pair (s i , s j ) which may not be really representative. Equation 12 may be problematic, especially since it might be susceptible to noise, due to the possibility of including long- distances with large stochastic errors.
To overcome these problems, we select only min(k, |S i |) and min(k, |S j |) closest leaves to the root of T i and T j with respect to the path length, respectively. To illustrate, for k = 3 we pick {1, 2} from T i and {4, 5, 6} from T j in Figure 7.
We now define

as the set of min(k, |S
i
|) closest leaves to the root of T
i
.  is called the k-representative leaf set. Hereafter, we estimate similar to Equation 4 the path length from the mrca of (T
i
, T
j
) to med as
is called the k-representative leaf set. Hereafter, we estimate similar to Equation 4 the path length from the mrca of (T
i
, T
j
) to med as

which is only based on the k-representative leaf sets. Now we can perform the clustering algorithm with reduced complexity. However, we also want to improve the preorder traversal procedure. The average path length from the unclassified object set S0(S
ij
) to the mrca of (T
i
, T
j
) is estimated by Equation 10 which also suffers from noise. To overcome this problem, we select only min(k, |S0(S
ij
)|) unclassified objects closest to the root of tree T{ij}with respect to distances  where s0 ∈ S0(S
ij
). We call the subset, denoted
where s0 ∈ S0(S
ij
). We call the subset, denoted  (S
ij
), k-representative unclassified object set.
(S
ij
), k-representative unclassified object set.
We now define

a shortest triplet, which contains three representatives of the three k-representative sets. By construction,  are close to the root of T{ij}and close to each other. Therefore, the edge length estimates based on shortest triplet {
are close to the root of T{ij}and close to each other. Therefore, the edge length estimates based on shortest triplet { } are less susceptible to estimation errors.
} are less susceptible to estimation errors.
We now rewrite Equation 10 to estimate the average path length from the representative unclassified object set

(S ij ) to the mrca of (T i , T j ) using only shortest triplets as



In short, the preorder traversal procedure uses only shortest triplets to estimate path lengths as well as edge lengths.
Shortest triplet clustering algorithm (STC)
We introduce now the shortest triplet clustering algorithm by combining the clustering algorithm, the local rearrangement, the k-representative sets, and the shortest triplets approach.
Shortest triplet clustering algorithm (STC)
-
Initial step:
-
(i): Find the median object med using Equation 7.
-
(ii): Set
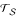 = {T1,..., T
n
} - {T
med
} and for each T
i
∈
= {T1,..., T
n
} - {T
med
} and for each T
i
∈ 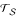 its representative leaf set
its representative leaf set  = {i}.
= {i}. -
(iii): Find for each T i ∈
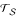 its potential neighbor Ti'∈
its potential neighbor Ti'∈ 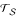 using Equation 8.
using Equation 8.
-
Selection step (largest path length criterion): Find the neighboring pair (
 ,
,  ) using Equation 9.
) using Equation 9. -
Agglomeration step:
-
(i): Combine
 and
and  into a new rooted tree
into a new rooted tree 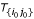 with root i0j0, and estimate new edge lengths of
with root i0j0, and estimate new edge lengths of 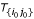 using Equation 5 based on shortest triplets.
using Equation 5 based on shortest triplets. -
(ii): Compute the k-representative leaf set
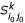 of
of 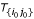 . based on k- representative leaf sets
. based on k- representative leaf sets 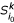 and
and 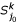 of
of  and
and  , respectively.
, respectively. -
(iii): Compute the k-representative unclassified object set
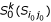 of
of 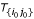 .
. -
(iv): Delete
 and
and  and add
and add 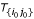 to
to 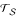 .
. -
(v): Find the potential neighbor for the new rooted tree
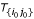 using Equation 8 based on representative sets, and replace Ti'for each T
i
∈
using Equation 8 based on representative sets, and replace Ti'for each T
i
∈ 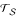 by
by 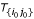 if
if 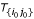 is its potential neighbor.
is its potential neighbor.
-
Local rearrangement step: Apply the preorder traversal procedure to the rooted subtrees
 and
and  of the new rooted tree
of the new rooted tree 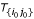 based on only shortest triplets.
based on only shortest triplets. -
Stopping step: If |
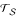 | > 1, goto Selection step, otherwise output the tree.
| > 1, goto Selection step, otherwise output the tree.
The complexity of STC
Now we briefly describe the complexity of the STC. At the initial step, (i), (ii), and (iii) are done in O(n2), O(n) and O(n2) time, respectively. Thus, the complexity of the initial step is O(n2). The selection step is done in O(n). At the agglomeration step, (i), (ii), (iii), (iv), and (v) are done in O(k3), O(k), O(nk2), O(1), and O(nk2) time, respectively. Thus, the complexity of the agglomeration step is O(nk2 + k3). Finally, we are estimating the complexity of the preorder traversal procedure based on only shortest triplets. Step 1 is done in constant time. Step 2, the nearest neighbor interchange operation around the root of T
i
costs O(k3). Estimating new edge lengths is done in O(k3) time. Re-computing the k-representative leaf set  of T
i
based on k-representative leaf sets of its rooted subtrees T
x
and T
y
costs O(k) time. Finally, re-computing the k-representative unclassified object set
of T
i
based on k-representative leaf sets of its rooted subtrees T
x
and T
y
costs O(k) time. Finally, re-computing the k-representative unclassified object set  (S
i
) of T
i
based on the k-representative leaf set
(S
i
) of T
i
based on the k-representative leaf set  of T
j
and the k-representative unclassified object set
of T
j
and the k-representative unclassified object set  (S
ij
) of T{ij}is done in O(k) time. Thus, the complexity of step 2 is O(k3). Step 3 is done in constant time. Step 1, step 2, and step 3 are repeated O(n) times so the complexity of the preorder traversal procedure is O(nk3).
(S
ij
) of T{ij}is done in O(k) time. Thus, the complexity of step 2 is O(k3). Step 3 is done in constant time. Step 1, step 2, and step 3 are repeated O(n) times so the complexity of the preorder traversal procedure is O(nk3).
In the STC algorithm, the selection step, the agglomeration step and the local rearrangement step are repeated (n - 2) times so the overall complexity of the STC algorithm is O(n2k3). Practically, we chose k = 5 as a good compromise between the accuracy and computational complexity for all data sets. That is, the practical complexity of the STC algorithm is only O(n2).
References
Saitou N, Nei M: The Neighbor – joining Method: A New Method for Reconstructing Phylogenetic Trees. Mol Biol Evol 1987, 4: 406–425.
Strimmer K, von Haeseler A: Quartet Puzzling: A Quartet Maximum – Likelihood Method for Reconstructing Tree Topologies. Mol Biol Evol 1996, 13: 964–969.
Gascuel O: BIONJ: An Improved Version of the NJ Algorithm Based on a Simple Model of Sequence Data. Mol Biol Evol 1997, 14: 685–695.
Huson DH, Nettles SM, Warnow TJ: Disk-Covering, a Fast-Converging Method for Phylogenetic Reconstruction. J Comput Biol 1999, 6: 369–386. 10.1089/106652799318337
Bruno WJ, Socci ND, Halpern AL: Weighted Neighbor Joining: A Likelihood Based-Approach to Distance-Based Phylogeny Reconstruction. Mol Biol Evol 2000, 17: 189–197.
Desper R, Gascuel O: Fast and Accurate Phylogeny Reconstruction Algorithms Based on the Minimum-Evolution Principle. J Comput Biol 2002, 9: 687–706. 10.1089/106652702761034136
Csürös M: Fast Recovery of Evolutionary Trees with Thousands of Nodes. J Comput Biol 2002, 9: 277–297. 10.1089/10665270252935467
Guindon S, Gascuel O: A Simple, Fast and Accurate Algorithm to Estimate Large Phylogenies by Maximum Likelihood. Syst Biol 2003, 52: 696–704. 10.1080/10635150390235520
Stamatakis A, Ludwig T, Meier H: RAxML-III: A fast program for maximum likelihood-based inference of large phylogenetic trees. Bioinformatics 2005, 21: 456–463. 10.1093/bioinformatics/bti191
Vinh LS, von Haeseler A: IQPNNI: Moving fast through tree space and stopping in time. Mol Biol Evol 2004, 21: 1565–1571. 10.1093/molbev/msh176
Vinh LS, Schmidt HA, von Haeseler A: PhyNav: A Novel Approach to Reconstruct Large Phylogenies. In Proceedings of the 28th Annual German Classification Society Conference (GfKl 2004). Dortmund, Germany; 2004:in press.
Charleston MA: Hitch-Hiking: A Parallel Heuristic Search Strategy, Applied to the Phylogeny Problem. J Comput Biol 2001, 8: 79–91. 10.1089/106652701300099137
Brauer MJ, Holder MT, Dries LA, Zwickl DJ, Lewis PO, Hillis DM: Genetic Algorithms and Parallel Processing in Maximum-Likelihood Phylogeny Inference. Mol Biol Evol 2002, 19: 1717–1726.
Schmidt HA, Strimmer K, Vingron M, von Haeseler A: TREE-PUZZLE: Maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics 2002, 18: 502–504. 10.1093/bioinformatics/18.3.502
Schmidt HA, von Haeseler A: Maximum Likelihood Analysis Using TREE-PUZZLE. In Current Protocols in Bioinformatics. Edited by: Baxevanis AD, Davison DB, Page RDM, Stormo G, Stein L. New York, USA: Wiley and Sons; 2003:6.6.1–6.6.25.
Cavalli-Sforza L, Edwards AWF: Phylogenetic analysis: Models and estimation procedures. Am J Hum Genet 1967, 19: 233–257.
Fitch W, Margoliash E: Construction of Phylogenetic trees. Science 1967, 155: 279–284.
Hartigan AJ: Clustering Algorithms. John Wiley and Sons, Inc; 1975.
Farris J: On the phenetic approach to vertebrate classification. 1977, 17: 823–850.
Klotz NKRB LC, Mitchell RM: Calculation of evolutionary trees from sequence data. Proc Natl Acad Sci USA 1979, 76: 4516–4520.
Li WH: Simple method for constructing phylogenetic trees from distance matrices. Proc Natl Acad Sci USA 1981, 78: 1085–1089.
Rambaut A, Crassly NC: Seq-Gen: An application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput Appl Biosci 1997, 13: 235–238.
Kimura M: A Simple Method for Estimating Evolutionary Rates of Base Substitutions through Comparative Studies of Nucleotide Sequences. J Mol Evol 1980, 16: 111–120.
Harding EF: The probabilities of rooted tree-shapes generated by random bifurcation. Adv Appl Prob 1971, 3: 44–77.
Swofford DL, Olsen GJ, Waddell PJ, Hillis DM: Phylogeny Reconstruction. In Molecular Systematics. 2nd edition. Edited by: Hillis DM, Moritz C, Mable BK. Sunderland, Massachusetts: Sinauer Associates; 1996:407–514.
Felsenstein J: PHYLIP (Phylogeny Inference Package) version 3.5c. Department of Genetics, University of Washington, Seattle 1993. [http://evolution.genetics.washington.edu/phylip.html]
Robinson DR, Foulds LR: Comparison of phylogenetic trees. Mathematical Biosciences 1981, 53: 131–147. 10.1016/0025-5564(81)90043-2
Buneman P: The recovery of trees from measures of dissimilarity. In Mathematics in the archaeological and historical sciences. Edited by: Hodson, Lendall, Tautu. Edinburgh: Edinburgh university press; 1971.
Semple C, Steel M: Phylogenetics. OXFORD univerity press; 2003.
Felsenstein J: Inferring Phylogenies. Sunderland, Massachusetts: Sinauer Associates; 2004.
Aho AV, Hopcroft JE, Ullman JD: The Design and Analysis of Computer Algorithms. Addison-Wesley Publishing Company; 1974.
Acknowledgements
We would like to express special thanks to Heiko Schmidt for his technical support. We thank Gunter Weiss, Ingo Ebersberger, Tanja Gesell and Jutta Buschbom for carefully reading the manuscript. We acknowledge the use of supercomputing resources of the ZAM/NIC at the Research Center Jiilich. We thank three anonymous referees for helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
Both authors participated in the design of the study and performed the analysis. LSV implemented the algorithms. Both authors wrote and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Sy Vinh, L., von Haeseler, A. Shortest triplet clustering: reconstructing large phylogenies using representative sets. BMC Bioinformatics 6, 92 (2005). https://doi.org/10.1186/1471-2105-6-92
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2105-6-92










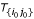 with root i0j0, and estimate new edge lengths of
with root i0j0, and estimate new edge lengths of 

 . The leaf set {1, 2} (or {4, 5, 6}) is the 3-representative leaf set of the rooted subtree
. The leaf set {1, 2} (or {4, 5, 6}) is the 3-representative leaf set of the rooted subtree 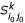 of
of 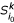 and
and 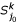 of
of 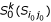 of
of