Background

Under a rapid increase of genome data, the need for accurate sequence alignment algorithms has become more and more important, and several methods have been developed. Sequence alignment algorithm is designed for mainly two purposes. One purpose is to design for comparing a query sequence with the database which contains preobtained sequences, and another is to design for generating multiple sequence alignment. FASTA [1] and BLAST [2], commonly used methods in molecular biology, are developed for database search, where a quick alignment algorithm is desired. For this quickness, the accuracy of alignment in these methods is lower than of the alignment by optimal algorithm.

In addition to for database search, sequence alignment is used for generating multiple alignment. In the multiple alignment, the accuracy is more important than the quickness. The recent popular multiple alignment methods, such as ClustalW [3], DIALIGN [4], TCoffee [5], MAFFT [6], MUSCLE [7], Probcons [8] and Probalign [9], are based on a "pairwise" alignment algorithm. In order to generate alignment with a realistic time and space costs, all of these methods use a progressive algorithm for constructing multiple alignment [10]. This "progressive" means to construct the multiple alignment by iterating pairwise alignment. These kind of methods give high accuracy for closely-related homologous sequences with identity more than 40%, but are not satisfied for distantly-related homologous sequences [11]. To improve the accuracy of the progressive algorithm, some measures based on, for instance, entropy [12] or consistency [13] have been developed. However, these measures are still not taken the intersite correlations of the sequences.

According to Anfinsen's dogma (also known as the thermodynamic hypothesis) [14], for a small globular protein, its three-dimensional structure is determined by the amino acid sequence of the protein. There may exist intersite correlations at least for two consecutive pairs of residues. Gonnet et al. considered this possibility [15]. We could improve alignment accuracy by taking into account information of the intersite correlations. Recently, Crooks et al. tried and tested such an approach [16], but they concluded that their approach is statistically indistinguishable from the standard algorithm. More recently, however, Lu and Sze proposed another approach [17], and they concluded that their strategy is able to consistently improve over existing algorithms on a few sets of benchmark alignments. Their approach is a kind of post processing algorithm. They take the average of the optimal values of the neighboring sites of one site, and they consider that the average value is the optimal value of that site. Note that they used usual "sum of pairs" measure for sequences. Their improvement of the accuracy in their tests was around 1~ 3% by using the BAliBASE 3.0 [18].

In this paper, we propose another approach introducing a new metric defined on compound systems of two sequences. Most of alignments are based on finding a path that gives the minimum value to the sum of difference (the maximum value to the sum of similarity) for each residue pair between two sequences. Our method is to change the way defining the difference (so, the sum) above by computing this sum of differences by introducing a quantity through the transition probability between consecutive pairs of residues. The comparison of our method with the method of Lu and Sze gives the following: In the very difficult range that the sequence identity is less than 15%, our method improves the accuracy nearly 8% up, but the Lu and Sze method improves it nearly 1% up.

A new measure taking the correlation of consecutive pairs of residues

First, let us establish some notations. Let Ω be the set of all amino acids, and Ω* be the Ω with the indel (gap) "*": Ω* ≡ Ω∪{*}. Let [Ω*] be the set of all sequences of the elements in Ω*. We call an element of Ω a residue and an element of Ω* a symbol. In addition, let Γ ≡ Ω × Ω be the direct product of two Ωs and Γ* ≡ Ω* × Ω*.

Consider two arranged sequences, A = a1a2 ... a n and B = b1b2 ... b n , both of length n, where a i , b j ∊ Ω*. We also denote the sequences by u1u2 ... u n , where u i = (a i , b i ) ∊ Γ*, and we call u i a site in the following discussion. In general, the relative likelihood that the sequences are related as opposed to being unrelated is known as the "odds ratio":

(1)

Here, p (a) is the occurrence probability of the given segment and p (a; b) is the joint probability that the two segments occur. In order to arrive at an additive scoring system, Equation (1) is typically simplified by assuming that the substitutions are independent of the location and there is no intersite correlations; namely, p (A) = ∏ p (a), p (B) = ∏ p (b) and p (A, B) = ∏ p (a, b). Thus the logarithm of Equation (1), known as the log-odds ratio, is now a sum of independent parts:

(2)

Where

(3)

is the log likelihood ratio of the symbol pair (a, b) occurring as an aligned pair to that occurring as an unaligned pair. The s (a, b) is called a score and S = (s (a, b)) is called a substitution matrix. These quantities (Equation (2) and (3)) are used to define a measure for pairwise sequence alignment [19]. Here, we define a normalized substitution matrix (i.e., every element in S takes the value between 0 and 1) and define a difference of A and B.

Let f s : [smin,smax ] ↦ R be a normalizing function:

(4)

Where

(5)
(6)

Let put (a, b) = f (s (a, b)) for a, b Ω. This (a, b) is a normalized expression of the score s (a, b). By using this quantity, we define a normalized substitution matrix as M = ( (a, b)). Then a difference of A and B is defined by

(7)

When the sequence A is equal to B the difference d sub (A, B) has a minimum value 0.

One of the essential assumption for the above approach (using a sum of independent parts as a difference of A and B) was the induction of the occurring probability. We could take more informative approach by including the intersite correlations. Crooks et al. tried one of such an approach [16]. They introduced a measure for two sequences based on a multivariate probability approximated by using the intersite relative likelihood. But, they concluded that their approach is statistically indistinguishable from the standard algorithm. We feel that their measure (equation (4) in their paper) is different from ours. To introduce their measure, they defined a type of joint probability. However it can not be a probability, bacause their quantity is the multiplication of likelihood "ratios", so it goes beyond more than 1. Moreover, we think that the intersite relative likelihood may not describe the difference of sequence A and B. Under an assumption that each site of the sequences has Markov property, we propose a new measure for two sequences by adding a transition effect and its weight ε (a degree of mixture):

(8)

where

(9)

Here we introduce a normalized transition (u i , ui+1) called "Transition Quantity", in order to simplify the equation. Let (u i , ui+1) be a normalized transition defined as

(10)
(11)

where f t (x; u) is a normalizing function:

(12)

By using the above quantity, a difference of A and B representing the "intersite transition" is defined as

(13)

Consequently, we define a difference measure for two sequences by combination of two differences dsub and dtrans:

(14)

Estimation of the Transition Quantity

Let us discuss how to estimate the transition quantity . We can estimate the transition quantity by collecting reliable aligned protein sequences. In this study, we estimated the transition quantity by means of the superfamilies subset of the dataset SABmark (version 1.63) [20]. This set covers the entire known fold space using only high-quality structures taken from the SCOP database [21]. For a large set, the same sequences are re-used in the set. In order to reduce the bias introduced by multiple use of the same sequences, we assign a weight to each sequence. This approach is similar to the one described in the paper [22]. If a sequence occurs N times in the dataset, its weight is N-1/2. We estimated the transition quantity from the weighted frequencies of observed transitions as follows.

Let L, Nbe the set of N sequences with length L:

Let = (a ik , a jk ) be in the finite set Γ* and it is a symbol pair in the k th site of the L, N. In addition, let be the set of all given sets L, N(i.e., the superfamilies set of the SABmark), and let N A be the frequency of the sequence A in the set .

Let : Γ* × Γ* ↦ R be a mapping which represents the weighted frequency appearing the symbols (u, v) in L, Nsuch that

(15)
(16)

Let p (v\u) be a transition probability from the symbol pair u to the pair v on such that

(17)

for u, v in the finite set Γ*.

We define a matrix T = ((u,v)) called "Transition matrix" by the elements (u, v) as

where t (u, v) = log p (v\u) and f t is the normalizing function defined by the equation (12).

MTRAP Algorithm

The MTRAP (sequence alignment method by a new M easure based on TRA nsition P robability) is an alignment algorithm by minimizing the value of a certain objective function based on the transition quantity (Figure 1). We describe the algorithm by means of dynamic programming [23].

Figure 1
figure 1

Illustration of MTRAP. The set of bold arrows indicates a possible route for alignment and the normal arrows indicate the transitions from a pair to the subsequent pair. A value (u) indicates a difference of two residues in a given pair u and (u1, u2) indicates the quantity based on a transition probability from a pair u1 to the subsequent pair u2. A conventional objective function such as "Sum of Pairs" is defined only by the sum of the value (u) of all possible pairs across the sequences, whereas our objective function in the MTRAP is defined by the sum of both (u) and (u1, u2) across the sequences (Equation (14)).

Full size image

Let A, B be two amino acid sequences such as

where a i , b j ∊ Ω. Take the lattice point P k = (i k , j k ), i = 1, ..., m, j = 1, ..., n as in Figure 2. We call the sequence of the lattice points

Figure 2
figure 2

Lattice points with two-sequences. The input amino acid sequences A = (a1 ⋯ a m ) and B = (b1 ⋯ b n ) are placed on each two axes. An initial point P1 (0,0) and a final point P N (m, n) are fixed.

Full size image
(18)

a "route" with an initial point P1 = (0, 0) and a final point P N = (m, n) if the following conditions are met:

(19)

Let α R , β R be maps from a route ℛ = {P1, P2, ..., P N } to a set Ω* such that

(20)
(21)

and μ R be a map from the route ℛ to the set of all symbol pairs Γ*(≡ Ω* × Ω*) such that

(22)

We call the following A* and B* the alignment of A and B by the route ℛ:

Let R(P) be the set of all routes with the final point P, that is,

(23)

Let us fix the following notations for the following discussion: (1) Γ*- ≡ Ω* × Ω, (2) Γ;-* ≡ Ω × Ω*, (3) Γg-≡ {*} × Ω, (4) Γ-g≡ Ω × {*}, (5) wopen is a constant called gap "opening" cost; 0 ≤ wopen ≤ 1, (6) wextend is a constant called gap "extending" cost; 0 ≤ wextend ≤ wopen and (7) ε is a weight, 0 ≤ ε ≤ 1 (i.e., the mixture of usual difference dsub and our new difference dtrans). The difference between A and B by a route ℛ is given by

(24)

where d s is a function from Γ* × Γ* to R such that

(25)
(26)
(27)

The degree of difference between A and B with respect to a final point P can be defined as

(28)

Hence the degree of difference between A and B is

(29)

We calculate D AB by a dynamic programming technique as below. For a final point P k = (i, j) and a route ℛ = {P1, ..., P k } ∊ R(P k ), we have

(30)

where Q1 = (i - 1, j), Q2 = (i -1, j - 1) and Q3 = (i, j -1). Therefore

(31)

with

(32)

for l = 1, 2, 3. Thus we obtain

(33)
(34)
(35)
(36)

where

(37)

for l = 1, 2, 3.

Each point Q l has three points which possibly go to Q l one step after. These points are precisely written as

(38)

when Q1 = (i -1, j), Q2 = (i -1, j -1), Q3 = (i, j - 1).

The distances D l (P k = (i, j)) can be obtained from one step before by the following recursion relations:

(39)
(40)
(41)

for l = 1, 2, 3. The values D l of initial point and those of the edge points are assumed as

(42)
(43)
(44)
(45)

Moreover for other special cases, the recursive relation of the edge points satisfies

(46)

for ℛ ∊ R1 (P k ), i = 1, ..., m,

(47)

for ℛ ∊ R3 (P k ), j = 1, ..., n.

This calculation is completed in mn steps.

Multiple sequence alignment by MTRAP

In order to discuss the effect of using MTRAP algorithm in the iteration step of progressive multiple alignment, we modified the TCoffee [5], a consistency-based progressive multiple alignment program, by means of our distance (Equation (14)). TCoffee constructs a primary library (pairwise alignments between all of the sequences to be aligned) at first step. We implemented our algorithm to make this primary library. That is, our modified TCoffee constructs a multiple alignment by following steps.

  1. 1.

    Generating a primary library by using MTRAP

  2. 2.

    Extending the library (Calculate a consistency)

  3. 3.

    Making a guide tree for the progressive step

  4. 4.

    Constructing a multiple alignment by progressive strategy

The modified TCoffee uses the extended library obtained by the MTRAP algorithm for aligning.

Performance evaluation

We compared the performance of MTRAP to those of the most often used nine methods: Needle, ClustalW2, MAFFT, TCoffee, DIALIGN, MUSCLE, Probcons, Probalign and TCoffee-Lu/Sze. The details of these nine methods are: (1) Needle, a global pairwise alignment using Needleman-Wunsch algorithm [24] contained in EMBOSS package ver. 5.0.0 [25]; (2) ClustalW2 [3, 26], a typical progressive multiple alignment method; (3) MAFFT ver. 6 [6], a fast method with Fourier transform algorithm; (4) TCoffee ver. 5.31 [5], a heuristic consistency-based method that combines global and local alignments; (5)

DIALIGN ver. 2.2 [4], a method with segment-segment approach; (6) MUSCLE ver. 3.7 [7], a method with Log-Expectation algorithm; (7) Probcons ver. 1.12 [8], a probabilistic consistency-based method, (8) Probalign ver. 1.1 [9], a multiple sequence alignment using partition function posterior probabilities and (9) TCoffee-Lu/Sze, an improved TCoffee modified by the Lu/Sze algorithm [17]. These programs without MAFFT used their default parameters and MAFFT used "L-IN-i" strategy mode.

To measure the accuracy of each method, we used three different databases: HOMSTRAD (version November 1, 2008) [27, 28], PREFAB 4.0 [7] and BAliBASE 3.0 [18]. These are the databases of structure-based alignments for homologous families. We used the all 630 pairwise alignments obtained from the HOMSTRAD for pairwise alignment tests, and used the all 1031 multiple alignments obtained from this database for multiple alignment tests. We also used the all 1682 protein pairs obtained from the PREFAB 4.0 for pairwise alignment tests. The BAliBASE 3.0 contains 5 different reference sets of alignment for testing multiple sequence alignment methods. We used the BBS sets included in the references 1,2,3 and 5. The BBS sets are described as being trimmed to homologous regions.

In order to avoid using the same dataset for training and test, We estimated the transition quantity by using the superfamilies subset from the dataset SABmark, which is described in the section "Estimation of the Transition Quantity". We also used this dataset for optimizing the parameters wopen, wextend, ϵ. Consequently, MTRAP uses the followings for parameter values: wopen = f s (-11), wextend = f s (-0.3) and ε = 0.775.

Alignment accuracy was calculated with the Q (quality) score [7]. The Q score is defined as the ratio of the number of correctly aligned residue pairs in the test alignment (i.e., the alignment obtained by a specified algorithm such as MTRAP, Needle, etc.) to the total number of aligned residue pairs in the reference alignment. When all pairs are correctly aligned, the score have a maximum value 1, and when no-pairs are aligned the score have a minimum value 0. This score has previously been called the SPS (Sum of Pairs Score) [29] or the developer score [30]. Let us redefined this score in our notations. Let A i (i = 1, i..., N) indicates the i th sequence of the reference alignment with length L, and let a ik ∊ Ω* indicates the k th symbol in the sequence A i . When a ik ≠ *, it is important to find the number of the site in the test sequence corresponding to the symbol a ik , whose numbers are denoted by n ik . When a ik = *, put n ik = 0 (i = 1, ..., N). Then the Q score is given as

Implementation

The MTRAP algorithm is implemented as a C++ program. The program has been tested in several types of Linux machines including 32-bit ×86 platform and also has been tested on Mac OSX snow leopard (64-bit). The program has a number of command-line options, e.g., the option setting the value of a parameter such that , , ε, wopen, wextend, and the option controlling the output format. The program accepts only multiple-fasta format as an input format.

Results and Discussion

Performance evaluation of pairwise alignment

We compared MTRAP with nine different alignment methods including the modified TCoffee by using all 1682 protein pairs of PREFAB 4.0 and all 630 protein pairs of HOMSTRAD. We used GONNET250 matrix with the MTRAP. The similarity between the test alignment (sequence alignment by each method) and the reference alignment (obtained from PREFAB 4.0 or HOMSTRAD) was measured with the Q score. Suppose as usual that the reference alignment is the optimal alignment, the results of PREFAB 4.0 (Table 1) and those of HOMSTRAD (Table 2) indicate that our method works well compared with other methods. Our method achieves the highest ranking compared with all other methods except only one range 30-45%. Especially for the identity range 0-15%, MTRAP is 4 ~ 5% accurate than the 2nd ranking method. For the identity range 30-45%, Probcons and Probalign perform slightly better (~ 1%).

Table 1 Average Q scores on the PREFAB 4.0 database.
Full size table
Table 2 Average Q scores on the HOMSTRAD database (Pairwise only).
Full size table

Performance evaluations using other substitution matrices

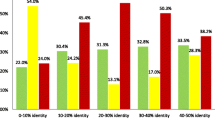
We did the performance evaluations using three different substitution matrix series: PAM, BLOSUM and GONNET, with HOMSTRAD and PREFAB 4.0, whose results are shown in Table 3 and Figure 3, respectively. We compared MTRAP with two typical global alignment programs, Needle and ClustalW2, which can use various substitution matrices. We used all 630 protein pairs of HOMSTRAD and all 1682 protein pairs of PREFAB 4.0. The similarity between the test alignment and the reference alignment was measured with the Q score.

Table 3 Average Q scores in pairwise alignment tests with typical substitution matrices.
Full size table
Figure 3
figure 3

The ratios of the average Q scores on the PREFAB 4.0 database. The upper two figures show the ratio of the average Q score by MTRAP to that by Needle and the ratio of ours to that by ClustalW2, both for PAM substitution matrix. The middle two figures show the ratios for BLOSUM substitution matrix. The last figure shows the ratio for GONNET substitution matrix.

Full size image

For every typical substitution matrix (i.e., PAM250, BLOSUM62 and GONNET250), MTRAP has more than 80% accuracy (e.g., 0.817 with PAM250 and BLOSUM62), whereas Needle and ClustalW2 have less than 80% accuracy (e.g., Needle has 0.763 with PAM250 and 0.768 with BLOSUM62) (Table 3). Moreover, it is important to notice that for two sequences with less than 30% sequence identity, our method improves the alignment accuracy significantly. For instance, MTRAP with PAM250 matrix has 0.421 for 0-15% sequence identity and 0.655 for 15-30% sequence identity, and ClustalW2 with PAM250 matrix has 0.234 for 0-15% sequence identity and 0.528 for 15-30% sequence identity, respectively.

Figure 3 shows the results with another database PREFAB 4.0 that are the ratios of the average Q scores for each identity range. For all substitution matrices, these three programs show almost the same alignment accuracy when the sequence identity is more than 60%, whereas the ratio clearly shows that MTRAP has higher accuracy than other programs in decreasing the sequence identity within 0-60%. For instance, MTRAP and Needle with PAM120 have 0.356 and 0.152 for 0-20% sequence identity, and those with BLOSUM80 have 0.363 and 0.166, respectively. For alignments with sequence identity 0-20%, the average Q score of MTRAP is 1.5-2.3 times more accurate than that of Needle. Moreover, MTRAP outperforms ClustalW2 at the same range by 1.4, 1.3 and 1.1-1.2 times for PAM, BLOSUM and GONNET series, respectively.

Performance of MTRAP algorithm for multiple alignment

We modified the TCoffee by means of our MTRAP algorithm. Table 4 and Table 5 show the accuracy of the modified TCoffee (TCoffee-MTRAP) compared with other methods including the original TCoffee with HOMSTRAD and BAliBASE 3.0. For all testing datasets, TCoffee-MTRAP shows the performance increase over the original TCoffee. Especially for the identity range 0-15%, TCoffee-MTRAP is 8.0% more accurate than the original TCoffee with HOMSTRAD, whereas the TCoffee modified by the Lu/Sze algorithm (TCoffee-Lu/Sze) is 0.7% more accurate than the original (Table 4). Also for V1 (i.e., the sequence identity is less than 20%) of the reference 1, TCoffee-MTRAP is 6.0% more accurate than the original TCoffee on BAliBASE 3.0, whereas TCoffee-Lu/Sze is 0.3% more accurate than the original (Table 5). In some domains, the two methods Probcons and Probalign, both of which are based on the probabilistic consistency strategy, are more accurate than TCoffee-MTRAP. Note that these two methods use the parameter values estimated from the BAliBASE 2.0 database.

Table 4 Average Q scores on the HOMSTRAD database.
Full size table
Table 5 Average Q scores on the BAliBASE 3.0 database.
Full size table

Conclusions

MTRAP is a global alignment method that is based on a new metric. The metric is determined by an adjusted substitution matrix and a transition probability-based matrix between two consecutive pairs of residues including gap-residue derived from structure-based alignments.

We indicated here that our approach, which takes into account an intersite correlation on the sequences, leads to a significant increase in the alignment accuracy, especially, for the low identity range. We also indicated that the MTRAP improves the alignment accuracy for any substitution matrices. Moreover, we confirmed that our algorithm works well together with a consistency based progressive approach for constructing multiple alignment.

However, the methods Probcons and Probalign were more accurate than TCoffee-MTRAP in some multiple alignment tests. The probabilistic consistency strategy is an improved consistency strategy of TCoffee. Therefore, combining MTRAP pairwise algorithm with the probabilistic consistency strategy will generate more high quality multiple alignments. We will examine this fact in a separate paper.

MTRAP has the similar calculation cost with other pairwise methods. That is, MTRAP has O (mn) calculation order for two input sequences with length m and n. Our CPU time shown in the Tables 1, 2 are almost the same as others.

Pairwise sequence alignment is among the most important technique to perform biological sequence analysis, and is fundamental to other applications in bioinformatics. Any multiple sequence alignment that is gradually built up by aligning pairwise sequences is essentially based on high-quality pairwise sequence alignments. By modifying common multiple alignment method based on our algorithm as shown in this paper, the accuracy was improved significantly. Moreover, we think that our technique is applicable to not only global alignment, but also some others such as, local homology search and motif-finding, which will be our future works.

Availability and requirements

Project name: MTRAP

Project home page: http://www.rs.noda.tus.ac.jp/%7Eohya-m/

Operating systems: Linux, UNIX

Programming languages: C++

License: BSD license