Quasi-log concavity conjecture and its applications in statistics

Abstract

This paper is motivated by several interesting problems in statistics. We first define the concept of quasi-log concavity, and a conjecture involving quasi-log concavity is proposed. By means of analysis and inequality theories, several interesting results related to the conjecture are obtained; in particular, we prove that log concavity implies quasi-log concavity under proper hypotheses. As applications, we first prove that the probability density function of k-normal distribution is quasi-log concave. Next, we point out the significance of quasi-log concavity in the analysis of variance. Next, we prove that the generalized hierarchical teaching model is usually better than the generalized traditional teaching model. Finally, we demonstrate the applications of our results in the research of the allowance function in the generalized traditional teaching model.

MSC:26D15, 62J10.

1 Introduction

Convexity and concavity are essential attributes of functions, their research and applications are important topics in mathematics (see [1–12]).

There are many types of convexity and concavity, one of them is log concavity which has many applications in statistics (see [2, 4, 7–12]). In [4], the authors apply the log concavity to study the Roy model, and some interesting results are obtained (see p.1128 in [4]), which include the following: If D is a log concave random variable, then

$$\frac{\partial Var[D|D>d]}{\partial d}⩽0\text{and}\frac{\partial Var[D|D⩽d]}{\partial d}⩾0.$$

(1.1)

Recall the definitions of log-concave function (see [1–5]) and β-log-concave function (see [13]): If the function $p:I\to (0,\mathrm{\infty })$ satisfies the inequality

$$p[\theta u+(1-\theta )v]⩾e^{\beta }{p}^{\theta }(u)p^{1-\theta }(v),\mathrm{\exists }\beta \in [0,\mathrm{\infty }),\mathrm{\forall }(u,v)\in I^2,\mathrm{\forall }\theta \in [0,1],$$

(1.2)

then we say that the function $p:I\to (0,\mathrm{\infty })$ is a β-log-concave function. 0-log-concave function is called a log-concave function. In other words, the function $p:I\to (0,\mathrm{\infty })$ is a log-concave function if and only if the function logp is a concave function. If $-logp$ is a concave function, then we call the function $p:I\to (0,\mathrm{\infty })$ a log-convex function. Here I is an interval (or high dimension interval).

For the log-concave function, we have the following results (see [5]). Let the function $p:I\to (0,\mathrm{\infty })$ be differentiable, where I is an interval. Then the function p is a log-concave function if and only if the function ${(logp)}^{\prime }$ is decreasing, i.e., if $v_1,v_2\in I$, $v_1<v_2$, then we have

$${[logp(v_1)]}^{\prime }⩾{[logp(v_2)]}^{\prime }.$$

(1.3)

Let the function $p\to (0,\mathrm{\infty })$ be twice differentiable. Then the function p is a log-concave function if and only if

$$p(x)p^{″}(x)-{[p^{\prime }(x)]}^2⩽0,\mathrm{\forall }x\in I.$$

(1.4)

Let for convenience that

$$\begin{array}{c}p\triangleq p(x),{\int }_a^{b}p\triangleq {\int }_a^{b}p(x)\mathrm{d}x,p^{\prime }(x)\triangleq \frac{\mathrm{d}p(x)}{\mathrm{d}x},p^{″}(x)\triangleq \frac{{\mathrm{d}}^{2}p(x)}{\mathrm{d}{x}^2},\hfill \\ p^{‴}(x)\triangleq \frac{{\mathrm{d}}^{3}p(x)}{\mathrm{d}{x}^3},p^{(n)}(x)\triangleq \frac{{\mathrm{d}}^{n}p(x)}{\mathrm{d}{x}^n},n⩾4.\hfill \end{array}$$

It is well known that there is a wide range of applications of log concavity in probability and statistics theories (see [2, 4, 7–12]). However, quasi-log concavity also has fascinating significance in probability and statistics theories, see Section 4 and Section 5. The main object of this paper is to introduce the quasi-log concavity of a function and demonstrate its applications in the analysis of variance.

Now we introduce the definition of quasi-log concavity and quasi-log convexity as follows.

Definition 1.1 A differentiable function $p:I\to (0,\mathrm{\infty })$ is said to be quasi-log concave if the following inequality

$$G_p[a,b]\triangleq \left({\int }_a^{b}p\right)[p^{\prime }(b)-p^{\prime }(a)]-{[p(b)-p(a)]}^2⩽0,\mathrm{\forall }a,b\in I$$

(1.5)

holds, here I is an interval. If inequality (1.5) is reversed, then the function $p:I\to (0,\mathrm{\infty })$ is said to be quasi-log convex.

We remark here if the function $p:I\to (0,\mathrm{\infty })$ is twice continuously differentiable, then inequality (1.5) can be rewritten as follows:

$$G_p[a,b]\triangleq {\int }_a^{b}p{\int }_a^b{p}^{″}-{\left({\int }_a^b{p}^{\prime }\right)}^2⩽0,\mathrm{\forall }a,b\in I.$$

(1.6)

Now we show that for the twice continuously differentiable function, quasi-log concavity implies log concavity, and quasi-log convexity implies log convexity.

Indeed, suppose that $p:I\to (0,\mathrm{\infty })$ is twice continuously differentiable and quasi-log concave. Then (1.6) holds. Hence

$$p(x)p^{″}(x)-{[p^{\prime }(x)]}^2=\underset{b\to x}{lim}\frac{1}{{(b-x)}^2}\{{\int }_x^{b}p(t)\mathrm{d}t{\int }_x^b{p}^{″}(t)\mathrm{d}t-{[{\int }_x^b{p}^{\prime }(t)\mathrm{d}t]}^2\}⩽0$$

for all $x\in I$ so that

$$\frac{{\mathrm{d}}^{2}logp(x)}{\mathrm{d}{x}^2}=\frac{p(x)p^{″}(x)-{[p^{\prime }(x)]}^2}{p^2(x)}⩽0,\mathrm{\forall }x\in I.$$

Therefore, (1.4) holds and p is log concave on I. Similarly, we can prove that quasi-log convexity implies log convexity.

On the other hand, we can prove that for the twice continuously differentiable function log convexity implies quasi-log convexity.

Indeed, suppose that $p:I\to (0,\mathrm{\infty })$ is twice continuously differentiable and log convex. Then (1.4) is reversed. Hence

$$\begin{array}{r}p(x)p^{″}(x)-{[p^{\prime }(x)]}^2⩾0,\mathrm{\forall }x\in I\\ \Rightarrow p^{″}(x)⩾0,|p^{\prime }(x)|⩽\sqrt{p(x)p^{″}(x)},\mathrm{\forall }x\in I\\ \Rightarrow {\left({\int }_a^b{p}^{\prime }\right)}^2⩽{\left({\int }_a^b\right|p^{\prime }\left|\right)}^2⩽{\left({\int }_a^b\sqrt{p{p}^{″}}\right)}^2⩽{\int }_a^{b}p{\int }_a^b{p}^{″},\mathrm{\forall }a,b\in I,\end{array}$$

that is, inequality (1.6) is reversed, here we used the Cauchy inequality

$${\left({\int }_a^{b}fg\right)}^2⩽{\int }_a^b{f}^2{\int }_a^b{g}^2.$$

Therefore, p is quasi-log convex on I.

Unfortunately, we have not found the connection between quasi-log concavity and β-log concavity, where $\beta >0$.

Based on the above analysis, we have reason to propose a conjecture (abbreviated as quasi-log concavity conjecture) as follows.

Conjecture 1.1 (Quasi-log concavity conjecture)

Suppose that the function $p:I\to (0,\mathrm{\infty })$ is twice continuously differentiable. If p is log concave, then p is quasi-log concave. Here I is an interval.

We have done a lot of experiments with mathematical software to verify the correctness of Conjecture 1.1, but did not find a counter-example.

We remark that similar concepts may be defined for sequences ${\{x_n\}}_{n=1}^{\mathrm{\infty }}\subseteq (0,\mathrm{\infty })$. We first define

$$\begin{array}{c}{x}_n^{\prime }\triangleq x_{n+1}-x_n,\mathrm{\forall }n\in \mathbb{N}\triangleq \{1,2,\dots \},\hfill \\ {\int }_a^b{x}_n\triangleq \sum _{a⩽n<b}{x}_n,\mathrm{\forall }a,b\in \mathbb{N},a<b,\hfill \\ G_{x_n}[a,b]\triangleq \left({\int }_a^b{x}_n\right)(x_b^{\prime }-x_a^{\prime })-{(x_b-x_a)}^2,\mathrm{\forall }a,b\in \mathbb{N},a<b,\hfill \end{array}$$

the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}\subseteq (0,\mathrm{\infty })$ is called a log-concave sequence if

$$x_a{x}_{a+2}-x_{a+1}^2⩽0,\mathrm{\forall }a\in \mathbb{N},$$

(1.7)

and is called quasi-log concave if

$$G_{x_n}[a,b]⩽0,\mathrm{\forall }a,b\in \mathbb{N},a<b.$$

(1.8)

Set $b=a+1$ in (1.8). Then (1.8) can be rewritten as (1.7). Hence for the sequence ${\{x_n\}}_{n=1}^{\mathrm{\infty }}\subseteq (0,\mathrm{\infty })$, quasi-log concavity implies log concavity. Similarly, we can define a log-convex sequence and quasi-log convexity of a sequence. We expect inter-relations between these concepts but they will be dealt with elsewhere.

In this paper, we are concerned with Conjecture 1.1 and demonstrate the applications of our results in the analysis of variance and the generalized hierarchical teaching model with generalized traditional teaching model. Our motivation is to study several interesting problems in statistics.

In Section 2, we take up Conjecture 1.1. In Section 3, we give several illustrative examples. In Section 4, we prove that the probability density function of the k-normal distribution is quasi-log concave. In Section 5, we demonstrate the applications of these results, we show that the generalized hierarchical teaching model is normally better than the generalized traditional teaching model (see Remark 5.3), and we point out the significance of quasi-log concavity in the analysis of variance and the generalized traditional teaching model.

2 Study of Conjecture 1.1

For Conjecture 1.1, we have the following five theorems.

Theorem 2.1 Let the function $p:I\to (0,\mathrm{\infty })$ be twice continuously differentiable, log concave and monotone. If

$$0<\underset{t\in I}{sup}\left\{\right|\left|{(logp)}^{\prime }\right|-\sqrt{-{(logp)}^{″}}\left|\right\}⩽\underset{t\in I}{inf}\left\{\right|{(logp)}^{\prime }|+\sqrt{-{(logp)}^{″}}\},$$

(2.1)

then p is quasi-log concave.

Proof Since the function p is log concave, we have

$$-{(logp)}^{″}=-{[logp(t)]}^{″}⩾0,\mathrm{\forall }t\in I,$$

so inequality (2.1) is well defined.

Without loss of generality, we may assume that

$$a,b\in I,a<b.$$

Note that for any positive real number λ and any real numbers x, y, we have the inequality

$$xy⩽{\left(\frac{{\lambda }^{2}x+y}{2\lambda }\right)}^2,$$

(2.2)

the equality holds if and only if ${\lambda }^{2}x=y$.

According to inequality (2.1), there exists a positive real number λ such that

$$0<\underset{t\in I}{sup}\left\{\right|\left|{(logp)}^{\prime }\right|-\sqrt{-{(logp)}^{″}}\left|\right\}⩽\lambda ⩽\underset{t\in I}{inf}\left\{\right|{(logp)}^{\prime }|+\sqrt{-{(logp)}^{″}}\}.$$

(2.3)

From (2.3) we know that for the positive real number λ, we have

$${\lambda }^{2}p(t)-2\lambda |p^{\prime }(t)|+p^{″}(t)⩽0,\mathrm{\forall }t\in I,$$

(2.4)

and

$${\lambda }^{2}p(t)+2\lambda |p^{\prime }(t)|+p^{″}(t)⩾0,\mathrm{\forall }t\in I.$$

(2.5)

Indeed, since

$${(logp)}^{\prime }=\frac{p^{\prime }}{p},{(logp)}^{″}=\frac{p{p}^{″}-{(p^{\prime })}^2}{p^2},\frac{p^{″}}{p}={\left[{(logp)}^{\prime }\right]}^2+{(logp)}^{″},$$

(2.6)

inequality (2.4) is equivalent to the inequalities

$$\left|{(logp)}^{\prime }\right|-\sqrt{-{(logp)}^{″}}⩽\lambda ⩽\left|{(logp)}^{\prime }\right|+\sqrt{-{(logp)}^{″}},\mathrm{\forall }t\in I,$$

(2.7)

and inequality (2.5) is equivalent to the inequalities

$$\lambda ⩾-\left[\right|{(logp)}^{\prime }|-\sqrt{-{(logp)}^{″}}],\mathrm{\forall }t\in I,$$

(2.8)

or

$$\lambda ⩽-\left[\right|{(logp)}^{\prime }|+\sqrt{-{(logp)}^{″}}],\mathrm{\forall }t\in I.$$

(2.9)

Hence if inequalities (2.3) hold, then both inequality (2.4) and inequality (2.5) hold. That is to say, inequalities (2.4) and (2.5) are equivalent to inequalities (2.3).

Since $p:I\to (0,\mathrm{\infty })$ is monotonic, we obtain that

$${\left({\int }_a^b{p}^{\prime }\right)}^2={\left({\int }_a^b\right|p^{\prime }\left|\right)}^2.$$

(2.10)

Combining with (2.2), (2.4), (2.5) and (2.10), we get

$$\begin{array}{r}{\int }_a^{b}p{\int }_a^b{p}^{″}-{\left({\int }_a^b{p}^{\prime }\right)}^2\\ ⩽{\left(\frac{{\lambda }^2{\int }_a^{b}p+{\int }_a^b{p}^{″}}{2\lambda }\right)}^2-{\left({\int }_a^b{p}^{\prime }\right)}^2\\ ={\left({\int }_a^b\frac{{\lambda }^{2}p+p^{″}}{2\lambda }\right)}^2-{\left({\int }_a^b\right|p^{\prime }\left|\right)}^2\\ =({\int }_a^b\frac{{\lambda }^{2}p+p^{″}}{2\lambda }+{\int }_a^b|p^{\prime }\left|\right)({\int }_a^b\frac{{\lambda }^{2}p+p^{″}}{2\lambda }-{\int }_a^b|p^{\prime }\left|\right)\\ =\frac{1}{4{\lambda }^2}\left[{\int }_a^b({\lambda }^{2}p+2\lambda |p^{\prime }|+p^{″})\right]\left[{\int }_a^b({\lambda }^{2}p-2\lambda |p^{\prime }|+p^{″})\right]\\ ⩽0.\end{array}$$

This means that inequality (1.6) holds.

The proof of Theorem 2.1 is completed. □

Corollary 2.1 Let the function $p:[\alpha ,\beta ]\to (0,\mathrm{\infty })$ be thrice continuously differentiable and log concave. If

$$p^{\prime }⩾0,p^{″}>0,{(logp)}^{‴}⩽-2{\left(\sqrt{-{(logp)}^{″}}\right)}^3,\mathrm{\forall }x\in [\alpha ,\beta ],$$

(2.11)

then the function $p:[\alpha ,\beta ]\to (0,\mathrm{\infty })$ is quasi-log concave.

Proof Let

$$\phi =\left|\right|{(logp)}^{\prime }|-\sqrt{-{(logp)}^{″}}|,\psi =\left|{(logp)}^{\prime }\right|+\sqrt{-{(logp)}^{″}}.$$

From (2.11), we have

$$\begin{array}{c}\phi ={(logp)}^{\prime }-\sqrt{-{(logp)}^{″}}=\frac{p^{\prime }-\sqrt{{(p^{\prime })}^2-p{p}^{″}}}{p}>0,\hfill \\ \psi ={(logp)}^{\prime }+\sqrt{-{(logp)}^{″}}⩾\phi >0,\hfill \\ \frac{\mathrm{d}\phi }{\mathrm{d}x}={(logp)}^{″}+\frac{{(logp)}^{‴}}{2\sqrt{-{(logp)}^{″}}}⩽0,\hfill \\ \frac{\mathrm{d}\psi }{\mathrm{d}x}={(logp)}^{″}-\frac{{(logp)}^{‴}}{2\sqrt{-{(logp)}^{″}}}⩾0,\hfill \end{array}$$

and

$$0<\phi (x)⩽\phi (\alpha )⩽\psi (\alpha )⩽\psi (x),\mathrm{\forall }x\in [\alpha ,\beta ],$$

hence

$$\begin{array}{rl}0& <\underset{x\in [\alpha ,\beta ]}{sup}\left\{\right|\left|{(logp)}^{\prime }\right|-\sqrt{-{(logp)}^{″}}\left|\right\}=\phi (\alpha )\\ ⩽\psi (\alpha )=\underset{x\in [\alpha ,\beta ]}{inf}\left\{\right|{(logp)}^{\prime }|+\sqrt{-{(logp)}^{″}}\}.\end{array}$$

By Theorem 2.1, the function $p:[\alpha ,\beta ]\to (0,\mathrm{\infty })$ is quasi-log concave. This ends the proof. □

Theorem 2.2 Let the function $p:[\alpha ,\beta ]\to (0,\mathrm{\infty })$ be twice continuously differentiable and log concave. If

$${(\beta -\alpha )}^2\underset{x\in [\alpha ,\beta ]}{sup}\left\{\right|{(logp(x))}^{″}{|}^2\}-2\underset{x\in [\alpha ,\beta ]}{inf}\left\{\right|{(logp(x))}^{″}\left|\right\}⩽0,$$

(2.12)

then $p:[\alpha ,\beta ]\to (0,\mathrm{\infty })$ is quasi-log concave.

Proof Now we prove that (1.6) holds as follows.

Without loss of generality, we assume that $a,b\in [\alpha ,\beta ]$ and $a<b$. Note that

$$\begin{array}{c}{G}_p[a,b]\triangleq {\int }_a^{b}p{\int }_a^b{p}^{″}-{\left({\int }_a^b{p}^{\prime }\right)}^2,\hfill \\ \frac{\partial G_p[a,b]}{\partial b}=p(b){\int }_a^b{p}^{″}+p^{″}(b){\int }_a^{b}p-2p^{\prime }(b){\int }_a^b{p}^{\prime },\hfill \end{array}$$

and

$$\frac{{\partial }^2{G}_p[a,b]}{\partial b\partial a}=-p(b)p^{″}(a)-p^{″}(b)p(a)+2p^{\prime }(b)p^{\prime }(a).$$

According to Lagrange mean value theorem, there are two real numbers $a_{\ast }$, $b_{\ast }$,

$$a_{\ast },b_{\ast }\in I\text{and}a<a_{\ast }<b_{\ast }<b,$$

such that

$$\frac{G_p[a,b]}{b-a}=\frac{G_p[a,b]-G_p[a,a]}{b-a}=\frac{\partial G_p[a,b_{\ast }]}{\partial b_{\ast }},$$

and

$$\frac{\frac{\partial G_p[a,b_{\ast }]}{\partial b_{\ast }}}{a-b_{\ast }}=\frac{\frac{\partial G_p[a,b_{\ast }]}{\partial b_{\ast }}-\frac{\partial G_p[b_{\ast },b_{\ast }]}{\partial b_{\ast }}}{a-b_{\ast }}=\frac{{\partial }^2{G}_p[a_{\ast },b_{\ast }]}{\partial b_{\ast }\partial a_{\ast }},$$

hence

$$G_p[a,b]=(b-a)(b_{\ast }-a)[p(b_{\ast })p^{″}(a_{\ast })+p^{″}(b_{\ast })p(a_{\ast })-2p^{\prime }(b_{\ast })p^{\prime }(a_{\ast })].$$

(2.13)

From (2.6) and the Lagrange mean value theorem, we get

$$\begin{array}{r}p(b_{\ast })p^{″}(a_{\ast })+p^{″}(b_{\ast })p(a_{\ast })-2p^{\prime }(b_{\ast })p^{\prime }(a_{\ast })\\ =p(a_{\ast })p(b_{\ast })\{{[{(logp(b_{\ast }))}^{\prime }-{(logp(a_{\ast }))}^{\prime }]}^2+{(logp(a_{\ast }))}^{″}+{(logp(b_{\ast }))}^{″}\}\\ =p(a_{\ast })p(b_{\ast })\{{[(b_{\ast }-a_{\ast }){(logp(\xi ))}^{″}]}^2+{(logp(a_{\ast }))}^{″}+{(logp(b_{\ast }))}^{″}\}\\ ⩽p(a_{\ast })p(b_{\ast })\{{(\beta -\alpha )}^2{\left[{(logp(\xi ))}^{″}\right]}^2+{(logp(a_{\ast }))}^{″}+{(logp(b_{\ast }))}^{″}\}\\ =p(a_{\ast })p(b_{\ast })\{{(\beta -\alpha )}^2{\left[{(logp(\xi ))}^{″}\right]}^2-|{(logp(a_{\ast }))}^{″}|-|{(logp(b_{\ast }))}^{″}\left|\right\}\\ ⩽p(a_{\ast })p(b_{\ast })[{(\beta -\alpha )}^2\underset{x\in [\alpha ,\beta ]}{sup}\left\{\right|{(logp(x))}^{″}{|}^2\}-2\underset{x\in [\alpha ,\beta ]}{inf}\left\{\right|{(logp(x))}^{″}\left|\right\}]\\ ⩽0,\end{array}$$

i.e.,

$$p(b_{\ast })p^{″}(a_{\ast })+p^{″}(b_{\ast })p(a_{\ast })-2p^{\prime }(b_{\ast })p^{\prime }(a_{\ast })⩽0,$$

(2.14)

where

$$\alpha ⩽a<a_{\ast }<\xi <b_{\ast }<b⩽\beta .$$

(2.15)

Combining with (2.13), (2.14) and (2.15), we get inequality (1.6).

This completes the proof of Theorem 2.2. □

Theorem 2.3 Let the function $\phi :(\alpha ,\beta )\to (-\mathrm{\infty },\mathrm{\infty })$ be thrice continuously differentiable. If

$${\phi }^{″}(x)>0,2{\phi }^{\prime }(x){\phi }^{″}(x)-{\phi }^{‴}(x)⩾0,\mathrm{\forall }x\in (\alpha ,\beta ),$$

(2.16)

then the function

$$p:(\alpha ,\beta )\to (0,\mathrm{\infty }),p(x)\triangleq c{e}^{-\phi (x)},c>0,$$

is quasi-log concave.

Proof Let

$$G_p[a,b]\triangleq {\int }_a^{b}p{\int }_a^b{p}^{″}-{\left({\int }_a^b{p}^{\prime }\right)}^2.$$

We just need to show that

$$G_p[a,b]⩽0,\mathrm{\forall }a,b\in (\alpha ,\beta ).$$

(2.17)

Since

$$G_p[a,b]\equiv G_p[b,a],G_p[a,a]=0,\mathrm{\forall }a,b\in (\alpha ,\beta ),$$

without loss of generality, we can assume that

$$\alpha <b<a<\beta ,c=1,$$

(2.18)

and a is a fixed constant.

Note that

$$logp(x)=-\phi ,\frac{\mathrm{d}logp(x)}{\mathrm{d}x}=\frac{p^{\prime }}{p}=-{\phi }^{\prime },$$

and

$$\frac{{\mathrm{d}}^{2}logp(x)}{\mathrm{d}{x}^2}=\frac{p{p}^{\prime }-{(p^{\prime })}^2}{p^2}=-{\phi }^{″}.$$

Hence

$$p^{\prime }(x)=-{\phi }^{\prime }p,\mathrm{\forall }x\in (\alpha ,\beta ),$$

(2.19)

and

$$p^{″}(x)=[{\left({\phi }^{\prime }\right)}^2-{\phi }^{″}]p,\mathrm{\forall }x\in (\alpha ,\beta ).$$

(2.20)

From

$$\frac{\partial G_p[a,b]}{\partial b}=p(b){\int }_a^b{p}^{″}+p^{″}(b){\int }_a^{b}p-2p^{\prime }(b){\int }_a^b{p}^{\prime },$$

(2.19) and (2.20), we may see that

$$\frac{\partial G_p[a,b]}{\partial b}=p(b)\{{\int }_a^b{p}^{″}+[{({\phi }^{\prime }(b))}^2-{\phi }^{″}(b)]{\int }_a^{b}p+2{\phi }^{\prime }(b){\int }_a^b{p}^{\prime }\}.$$

(2.21)

Let

$$F(a,b)\triangleq \frac{1}{p(b)}\frac{\partial G_p[a,b]}{\partial b}={\int }_a^b{p}^{″}+[{({\phi }^{\prime }(b))}^2-{\phi }^{″}(b)]{\int }_a^{b}p+2{\phi }^{\prime }(b){\int }_a^b{p}^{\prime }.$$

(2.22)

Then

$$\begin{array}{rcl}\frac{\partial F(a,b)}{\partial b}& =& p^{″}(b)+[{({\phi }^{\prime }(b))}^2-{\phi }^{″}(b)]p(b)+[2{\phi }^{\prime }(b){\phi }^{″}(b)-{\phi }^{‴}(b)]{\int }_a^{b}p\\ +2[{\phi }^{″}(b){\int }_a^b{p}^{\prime }+{\phi }^{\prime }(b)p^{\prime }]\\ =& 2[{({\phi }^{\prime }(b))}^2-{\phi }^{″}(b)]p(b)+[2{\phi }^{\prime }(b){\phi }^{″}(b)-{\phi }^{‴}(b)]{\int }_a^{b}p\\ +2\{{\phi }^{″}(b)[p(b)-p(a)]-{({\phi }^{\prime }(b))}^{2}p(b)\}\\ =& [2{\phi }^{\prime }(b){\phi }^{″}(b)-{\phi }^{‴}(b)]{\int }_a^{b}p-2{\phi }^{″}(b)p(a),\end{array}$$

i.e.,

$$\frac{\partial F(a,b)}{\partial b}=[2{\phi }^{\prime }(b){\phi }^{″}(b)-{\phi }^{‴}(b)]{\int }_a^{b}p-2{\phi }^{″}(b)p(a).$$

(2.23)

Based on assumption (2.16), ${\int }_a^{b}p<0$ and (2.23), we have

$$\frac{\partial F(a,b)}{\partial b}<0,\mathrm{\forall }b\in (\alpha ,a).$$

(2.24)

From (2.24), (2.18) and (2.22), we have

$$F(a,b)>F(a,a)=0,\frac{\partial G_p[a,b]}{\partial b}>0.$$

(2.25)

By (2.25) and (2.18), we get

$$G_p[a,b]<G_p[a,a]=0.$$

(2.26)

That is to say, inequality (2.17) holds.

We remark that the equality in (2.17) holds if and only if $a=b$.

The proof of Theorem 2.3 is completed. □

Theorem 2.4 Let the function $\phi :(\alpha ,\beta )\to (-\mathrm{\infty },\mathrm{\infty })$ be four times continuously differentiable. If

$${\phi }^{″}(x)>0,2{[{\phi }^{″}(x)]}^3-{\phi }^{(4)}(x){\phi }^{″}(x)+{[{\phi }^{‴}(x)]}^2⩾0,\mathrm{\forall }x\in (\alpha ,\beta ),$$

(2.27)

and

$$-\mathrm{\infty }⩽G_p[\alpha ,\beta ]\triangleq {\int }_{\alpha }^{\beta }p{\int }_{\alpha }^{\beta }{p}^{″}-{\left({\int }_{\alpha }^{\beta }{p}^{\prime }\right)}^2⩽0,$$

(2.28)

then the function

$$p:(\alpha ,\beta )\to (0,\mathrm{\infty }),p(x)\triangleq c{e}^{-\phi (x)},c>0,$$

is quasi-log concave, where c is a constant.

In order to prove Theorem 2.4, we need the following lemma.

Lemma 2.1 Under the assumptions of Theorem  2.4, if

$$\alpha <a<b<{\beta }_{\ast }<\beta ,$$

(2.29)

then we have

$$G_p[a,b]⩽max\{0,G_p[a,{\beta }_{\ast }]\}.$$

(2.30)

Proof Without loss of generality, we can assume that $c=1$ and a is a fixed constant.

We continue to use the proof of Theorem 2.3. Note that equation (2.23) can be rewritten as

$$\frac{\partial F(a,b)}{\partial b}={\phi }^{″}(b)\left({\int }_a^{b}p\right)F^{\ast }(a,b),$$

(2.31)

where

$$F^{\ast }(a,b)\triangleq 2{\phi }^{\prime }(b)-\frac{{\phi }^{‴}(b)}{{\phi }^{″}(b)}-\frac{2p(a)}{{\int }_a^{b}p}.$$

(2.32)

Based on assumption (2.27), ${\int }_a^{b}p>0$ and (2.32), we have

$$\begin{array}{rl}\frac{\partial F^{\ast }(a,b)}{\partial b}=& \frac{2{[{\phi }^{″}(b)]}^3-{\phi }^{(4)}(b){\phi }^{″}(b)+{[{\phi }^{‴}(b)]}^2}{{[{\phi }^{″}(b)]}^2}\\ +\frac{2p(a)p(b)}{{({\int }_a^{b}p)}^2}>0,\mathrm{\forall }b\in (a,{\beta }_{\ast }),\end{array}$$

(2.33)

which means that $F^{\ast }(a,b)$ is strictly increasing for the variable $b\in (a,{\beta }_{\ast })$.

From (2.32), we may see that

$$\underset{b\to a^{+}}{lim}{F}^{\ast }(a,b)=F^{\ast }(a,a^{+})=-\mathrm{\infty }.$$

(2.34)

We prove inequality (2.30) in two cases (A) and (B).

• (A) Assume that

  $$F^{\ast }(a,{\beta }_{\ast })>0.$$

  (2.35)

By (2.34), (2.35) and the intermediate value theorem, there exists only one number $b_{\ast }\in (a,{\beta }_{\ast })$ such that

$$F^{\ast }(a,b_{\ast })=0.$$

(2.36)

From (2.33) and (2.31), we get

$$a<b<b_{\ast }\Rightarrow F^{\ast }(a,b)<F^{\ast }(a,b_{\ast })=0\Rightarrow \frac{\partial }{\partial b}F(a,b)<0,$$

and

$$b_{\ast }<b<{\beta }_{\ast }\Rightarrow F^{\ast }(a,b)>F^{\ast }(a,b_{\ast })=0\Rightarrow \frac{\partial }{\partial b}F(a,b)>0,$$

hence $F(a,b)$ is strictly decreasing if $b\in (a,b_{\ast }]$ and strictly increasing if $b\in [b_{\ast },{\beta }_{\ast })$.

If $F(a,{\beta }_{\ast })⩽0$, since $F(a,a)=0$, we have

$$\begin{array}{c}a<b⩽b_{\ast }\Rightarrow F(a,b)<F(a,a)=0,\hfill \\ b_{\ast }⩽b<{\beta }_{\ast }\Rightarrow F(a,b)⩽F(a,{\beta }_{\ast })⩽0,\hfill \\ F(a,b)=\frac{1}{p(b)}\frac{\partial G_p[a,b]}{\partial b}⩽0,\mathrm{\forall }b\in (a,{\beta }_{\ast }),\hfill \\ \frac{\partial G_p[a,b]}{\partial b}⩽0,\mathrm{\forall }b\in (a,{\beta }_{\ast }),\hfill \end{array}$$

and

$$G_p[a,b]⩽G_p[a,a]=0,\mathrm{\forall }b\in (a,{\beta }_{\ast }).$$

This means that inequality (2.30) holds.

Now we assume that

$$F(a,{\beta }_{\ast })>0.$$

(2.37)

Note that $F(a,b)$ is strictly decreasing if $b\in (a,b_{\ast }]$, we have

$$b_{\ast }\in (a,b_{\ast }]\Rightarrow F(a,b_{\ast })<F(a,a)=0.$$

(2.38)

By (2.37), (2.38), $F(a,b)$ is strictly increasing if $b\in [b_{\ast },{\beta }_{\ast })$ and the continuity, we know that there exists a unique real number $b^{\ast }\in (b_{\ast },{\beta }_{\ast })$ such that

$$F(a,b^{\ast })=0.$$

(2.39)

Since

$$\begin{array}{c}a<b⩽b_{\ast }\Rightarrow F(a,b)<F(a,a)=0\Rightarrow \frac{\partial }{\partial b}{G}_p[a,b]=p(b)F(a,b)<0,\hfill \\ b_{\ast }<b<b^{\ast }\Rightarrow F(a,b)<F(a,b^{\ast })=0\Rightarrow \frac{\partial }{\partial b}{G}_p[a,b]=p(b)F(a,b)<0,\hfill \\ a<b<b^{\ast }\Rightarrow \frac{\partial }{\partial b}{G}_p[a,b]<0,\hfill \end{array}$$

and

$$b^{\ast }<b<\beta \Rightarrow F(a,b)>F(a,b^{\ast })=0\Rightarrow \frac{\partial }{\partial b}{G}_p[a,b]=p(b)F(a,b)>0,$$

we know that $G_p[a,b]$ is strictly decreasing if $b\in (a,b^{\ast }]$ and strictly increasing if $b\in [b^{\ast },{\beta }_{\ast })$, so that

$$G_p[a,b]⩽max\{G_p[a,a],G_p[a,{\beta }_{\ast }]\}=max\{0,G_p[a,{\beta }_{\ast }]\}.$$

(2.40)

This means that inequality (2.30) also holds.

• (B) Assume that

  $$F^{\ast }(a,{\beta }_{\ast })⩽0.$$

  (2.41)

Since $F^{\ast }(a,b)$ is strictly increasing for the variable $b\in (a,{\beta }_{\ast })$, we have

$$\begin{array}{c}{F}^{\ast }(a,b)<F^{\ast }(a,{\beta }_{\ast })⩽0,\mathrm{\forall }b\in (\alpha ,{\beta }_{\ast }),\hfill \\ \frac{\partial F(a,b)}{\partial b}={\phi }^{″}(b)\left({\int }_a^{b}p\right)F^{\ast }(a,b)⩽0,\mathrm{\forall }b\in (\alpha ,{\beta }_{\ast }),\hfill \\ F(a,b)⩽F(a,a)=0,\mathrm{\forall }b\in (\alpha ,{\beta }_{\ast }),\hfill \\ \frac{\partial G_p[a,b]}{\partial b}=p(b)F(a,b)⩽0,\mathrm{\forall }b\in (\alpha ,{\beta }_{\ast }),\hfill \end{array}$$

and

$$G_p[a,b]⩽G_p[a,a]=0⩽max\{0,G_p[a,{\beta }_{\ast }]\},\mathrm{\forall }b\in (\alpha ,{\beta }_{\ast }).$$

That is to say, inequality (2.30) still holds.

The proof of Lemma 2.1 is completed. □

The proof of Theorem 2.4 is now relatively easy.

Proof of Theorem 2.4 We just need to show that (2.17) holds. Without loss of generality, we assume that

$$\alpha <a<b<\beta ,c=1.$$

(2.42)

Let ${\alpha }_{\ast },{\beta }_{\ast }\in (\alpha ,\beta )$ such that

$$\alpha <{\alpha }_{\ast }<a<b<{\beta }_{\ast }<\beta .$$

(2.43)

By Lemma 2.1, inequality (2.30) holds.

We define the auxiliary function $p_{\ast }$ as follows:

$$p_{\ast }:(-\beta ,-\alpha )\to (0,\mathrm{\infty }),p_{\ast }(x)\triangleq c{e}^{-\phi (-x)},c>0.$$

Then, by (2.27), we have

$$\begin{array}{c}{[\phi (-x)]}^{″}={\phi }^{″}(-x)>0,\mathrm{\forall }x\in (-\beta ,-\alpha ),\hfill \\ {[\phi (-x)]}^{‴}=-{\phi }^{‴}(-x),{[\phi (-x)]}^{(4)}={\phi }^{(4)}(-x),\mathrm{\forall }x\in (-\beta ,-\alpha ),\hfill \end{array}$$

and

$$\begin{array}{r}2{\left\{{[\phi (-x)]}^{″}\right\}}^3-{[\phi (-x)]}^{(4)}{[\phi (-x)]}^{″}+{\left\{{[\phi (-x)]}^{‴}\right\}}^2\\ =2{[{\phi }^{″}(-x)]}^3-{\phi }^{(4)}(-x){\phi }^{″}(-x)+{[{\phi }^{‴}(-x)]}^2\\ ⩾0,\mathrm{\forall }x\in (-\beta ,-\alpha ).\end{array}$$

According to Lemma 2.1 and

$$-\beta <-{\beta }_{\ast }<-a<-{\alpha }_{\ast }<-\alpha ,$$

we get

$$G_{p_{\ast }}[-{\beta }_{\ast },-a]⩽max\{0,G_{p_{\ast }}[-{\beta }_{\ast },-{\alpha }_{\ast }]\}.$$

(2.44)

Since

$$G_{p_{\ast }}[-b,-a]={\int }_{-b}^{-a}p(-x)\mathrm{d}x{\int }_{-b}^{-a}{p}^{″}(-x)\mathrm{d}x-{[{\int }_{-b}^{-a}{p}^{\prime }(-x)\mathrm{d}x]}^2\equiv G_p[a,b],$$

we have

$$G_{p_{\ast }}[-{\beta }_{\ast },-a]=G_p[a,{\beta }_{\ast }],G_{p_{\ast }}[-{\beta }_{\ast },-{\alpha }_{\ast }]=G_p[{\alpha }_{\ast },{\beta }_{\ast }],$$

and inequality (2.44) can be rewritten as

$$G_p[a,{\beta }_{\ast }]⩽max\{0,G_p[{\alpha }_{\ast },{\beta }_{\ast }]\}.$$

(2.45)

Combining with inequalities (2.30) and (2.45), we get

$$G_p[a,b]⩽max\{0,G_p[a,{\beta }_{\ast }]\}⩽max\{0,G_p[{\alpha }_{\ast },{\beta }_{\ast }]\}.$$

(2.46)

In (2.46), set ${\alpha }_{\ast }\to \alpha$, ${\beta }_{\ast }\to \beta$, we get

$$G_p[a,b]⩽max\{0,G_p[\alpha ,\beta ]\}.$$

(2.47)

According to conditions (2.28) and (2.47), inequality (2.17) holds.

This completes the proof of Theorem 2.4. □

Theorem 2.5 Let the function $\phi :(\alpha ,\beta )\to (-\mathrm{\infty },\mathrm{\infty })$ be four times continuously differentiable. If

$$\underset{x\to \beta }{lim}\phi (x)=\mathrm{\infty },\underset{x\to \beta }{lim}\frac{{\phi }^{\prime }(x)}{e^{\phi (x)}}=0,\underset{x\to \beta }{lim}\frac{{[{\phi }^{\prime }(x)]}^2}{{\phi }^{″}(x)e^{\phi (x)}}=0,{\int }_{\alpha }^{\beta }p<\mathrm{\infty },$$

(2.48)

and (2.27) holds, then the function

$$p:(\alpha ,\beta )\to (0,\mathrm{\infty }),p(x)\triangleq c{e}^{-\phi (x)},c>0,$$

is quasi-log concave.

Proof We just need to show that (2.17) holds. Without loss of generality, we assume that

$$\alpha <a<b<\beta ,c=1.$$

(2.49)

Set ${\beta }_{\ast }\to \beta$ in Lemma 2.1, we have

$$G_p[a,b]⩽max\{0,G_p[a,\beta ]\}.$$

(2.50)

To complete the proof of inequality (2.17), by (2.50), we just need to show that

$$G_p[a,\beta ]⩽0,\mathrm{\forall }a\in (\alpha ,\beta ).$$

(2.51)

Now, we believe that the real number a is variable. By condition (2.48), we have

$$p^{\prime }(\beta )\triangleq \underset{x\to \beta }{lim}{p}^{\prime }(x)=0,p(\beta )\triangleq \underset{x\to \beta }{lim}p(x)=0$$

and

$$\begin{array}{rcl}{G}_p[a,\beta ]& =& \left({\int }_a^{\beta }p\right)[p^{\prime }(\beta )-p^{\prime }(a)]-{[p(\beta )-p(a)]}^2\\ =& -p^{\prime }(a){\int }_a^{\beta }p-{[p(a)]}^2\\ =& p(a)[{\phi }^{\prime }(a){\int }_a^{\beta }p-p(a)],\end{array}$$

i.e.,

$$G_p[a,\beta ]=p(a)\varphi (a),$$

(2.52)

where

$$\varphi (a)\triangleq {\phi }^{\prime }(a){\int }_a^{\beta }p-p(a),a\in (\alpha ,\beta ).$$

(2.53)

If ${\phi }^{\prime }(a)⩽0$, then $\varphi (a)<0$, (2.51) holds by (2.52). Here we assume that ${\phi }^{\prime }(a)>0$.

Note that

$$\begin{array}{rcl}\frac{\mathrm{d}\varphi (a)}{\mathrm{d}a}& =& {\phi }^{″}(a){\int }_a^{\beta }p-{\phi }^{\prime }(a)p(a)-p^{\prime }(a)\\ =& {\phi }^{″}(a){\int }_a^{\beta }p\\ >& 0.\end{array}$$

Since

$${\phi }^{″}(x)>0,\mathrm{\forall }x\in (\alpha ,\beta ),$$

the limit

$$\underset{a\to \beta }{lim}{\phi }^{\prime }(a)$$

exists.

If

$$0<{\phi }^{\prime }(a)⩽\underset{a\to \beta }{lim}{\phi }^{\prime }(a)<\mathrm{\infty },$$

from ${\int }_{\alpha }^{\beta }p<\mathrm{\infty }$, we have

$$\underset{a\to \beta }{lim}{\int }_a^{\beta }p=\underset{a\to \beta }{lim}({\int }_{\alpha }^{\beta }p-{\int }_{\alpha }^{a}p)=0$$

(2.54)

and

$$\underset{a\to \beta }{lim}{\phi }^{\prime }(a){\int }_a^{\beta }p=0.$$

(2.55)

If

$$\underset{a\to \beta }{lim}{\phi }^{\prime }(a)=\mathrm{\infty },$$

then, by (2.54), (2.48) and L’Hospital’s rule, we have

$$\begin{array}{rl}\underset{a\to \beta }{lim}{\phi }^{\prime }(a){\int }_a^{\beta }p& =\underset{a\to \beta }{lim}\frac{{\int }_a^{\beta }p}{{[{\phi }^{\prime }(a)]}^{-1}}\\ =\underset{a\to \beta }{lim}\frac{(\mathrm{d}{\int }_a^{\beta }p)/\mathrm{d}a}{(\mathrm{d}{[{\phi }^{\prime }(a)]}^{-1})/\mathrm{d}a}\\ =\underset{a\to \beta }{lim}\frac{-p(a)}{-{[{\phi }^{\prime }(a)]}^{-2}{\phi }^{″}(a)}\\ =\underset{x\to \beta }{lim}\frac{{[{\phi }^{\prime }(x)]}^2}{{\phi }^{″}(x)e^{\phi (x)}}\\ =0,\end{array}$$

that is to say, (2.55) also holds. Hence

$$\varphi (a)<\varphi (\beta )=\underset{a\to \beta }{lim}[{\phi }^{\prime }(a){\int }_a^{\beta }p-p(a)]=\underset{a\to \beta }{lim}{\phi }^{\prime }(a){\int }_a^{\beta }p=0.$$

By (2.52), inequality (2.51) holds.

The proof of Theorem 2.5 is completed. □

3 Four illustrative examples

In order to illustrate the connotation of quasi-log concavity, we give four examples as follows.

Example 3.1 The function

$$p:[0,\pi ]\to (0,\mathrm{\infty }),p(x)\triangleq exp(sinx)$$

is quasi-log concave.

Proof Indeed, if

$$x\in I^{\ast }\triangleq [0,\frac{\pi }{2}]\text{or}[\frac{\pi }{2},\pi ],$$

then $p(x)$ is twice continuous differentiable and log concave with monotonous function, and

$$\begin{array}{c}\left|\right|{(logp)}^{\prime }|-\sqrt{-{(logp)}^{″}}|=||cosx|-\sqrt{sinx}|⩽max\{|cosx|,\sqrt{sinx}\}⩽1,\hfill \\ \left|{(logp)}^{\prime }\right|+\sqrt{-{(logp)}^{″}}=|cosx|+\sqrt{sinx}⩾|cosx|+sinx=\sqrt{1+|sin2x|}⩾1,\hfill \end{array}$$

hence

$$0<\underset{x\in I^{\ast }}{sup}\left\{\right|\left|{(logp)}^{\prime }\right|-\sqrt{-{(logp)}^{″}}\left|\right\}=1=\underset{x\in I^{\ast }}{inf}\left\{\right|{(logp)}^{\prime }|+\sqrt{-{(logp)}^{″}}\}.$$

By Theorem 2.1, the function $p(x)$ is quasi-log concave. That is to say, for any $a,b\in I^{\ast }$, inequality (1.5) holds.

Let

$$0⩽a<\frac{\pi }{2}<b⩽\pi .$$

Since

$$p^{\prime }(b)<0<p^{\prime }(a),$$

inequality (1.5) still holds. The proof is completed. □

Example 3.2 The function

$$p:(0,\mathrm{\infty })\to (0,\beta ),p(x)\triangleq exp(arctanx)$$

is quasi-log concave, where

$$\beta =\frac{1}{9}(7+4\sqrt[3]{10}+\sqrt[3]{100})=2.251036399304479\dots$$

is the root of the equation

$$\frac{16x^3}{{(1+x^2)}^6}-\frac{2x{[\frac{48x^3}{{(1+x^2)}^4}-\frac{24x}{{(1+x^2)}^3}]}^2}{{(1+x^2)}^2}+{[-\frac{8x^2}{{(1+x^2)}^3}+\frac{2}{{(1+x^2)}^2}]}^2=0.$$

(3.1)

Proof Indeed, in Theorem 2.4, set $\phi (x)=-arctanx$, then

$$p(x)=exp[-\phi (x)],\mathrm{\forall }x\in (0,\beta ).$$

By means of Mathematica software, we get

$$\begin{array}{r}{\phi }^{″}(x)=\frac{2x}{{(1+x^2)}^2}⩾0,\mathrm{\forall }x\in (0,\beta ),\\ 2{[{\phi }^{″}(x)]}^3-{\phi }^{(4)}(x){\phi }^{″}(x)+{[{\phi }^{‴}(x)]}^2\\ =\frac{16x^3}{{(1+x^2)}^6}-\frac{2x{[\frac{48x^3}{{(1+x^2)}^4}-\frac{24x}{{(1+x^2)}^3}]}^2}{{(1+x^2)}^2}+{[-\frac{8x^2}{{(1+x^2)}^3}+\frac{2}{{(1+x^2)}^2}]}^2\\ ⩾0,\mathrm{\forall }x\in (0,\beta ],\end{array}$$

the equation holds if and only if $x=\beta$.

Since

$$0<{\int }_0^{\beta }p<\mathrm{\infty },$$

and

$$-\mathrm{\infty }⩽G_p[0,\beta ]\triangleq {\int }_0^{\beta }p{\int }_0^{\beta }{p}^{″}-{\left({\int }_0^{\beta }{p}^{\prime }\right)}^2=-7.095040628958467\dots <0,$$

so (2.27) and (2.28) hold. By Theorem 2.4, the function $p(x)$ is quasi-log concave. This ends the proof. □

Example 3.3 The function

$$p:(0,\mathrm{\infty })\to (0,\mathrm{\infty }),p(x)\triangleq x^{\alpha },$$

is quasi-log concave, where $\alpha >0$.

Proof Note that inequality (1.6) can be rewritten as

$$\frac{\alpha }{\alpha +1}(b^{\alpha +1}-a^{\alpha +1})(b^{\alpha -1}-a^{\alpha -1})-{(b^{\alpha }-a^{\alpha })}^2⩽0,\mathrm{\forall }a,b\in I.$$

(3.2)

If $0<\alpha ⩽1$, then

$$\frac{\alpha }{\alpha +1}(b^{\alpha +1}-a^{\alpha +1})(b^{\alpha -1}-a^{\alpha -1})⩽0,$$

inequality (3.2) holds. Let $\alpha >1$. Then

$$(b^{\alpha +1}-a^{\alpha +1})(b^{\alpha -1}-a^{\alpha -1})⩾0.$$

Since

$$0<\frac{\alpha }{\alpha +1}<1,$$

and

$$(b^{\alpha +1}-a^{\alpha +1})(b^{\alpha -1}-a^{\alpha -1})-{(b^{\alpha }-a^{\alpha })}^2=-a^{\alpha -1}{b}^{\alpha -1}{(a-b)}^2⩽0,$$

we have

$$\begin{array}{r}\frac{\alpha }{\alpha +1}(b^{\alpha +1}-a^{\alpha +1})(b^{\alpha -1}-a^{\alpha -1})-{(b^{\alpha }-a^{\alpha })}^2\\ ⩽(b^{\alpha +1}-a^{\alpha +1})(b^{\alpha -1}-a^{\alpha -1})-{(b^{\alpha }-a^{\alpha })}^2\\ ⩽0,\end{array}$$

that is to say, inequality (3.2) still holds. The proof is completed. □

Example 3.4 The function

$$p:(0,\mathrm{\infty })\to (0,\mathrm{\infty }),p(x)\triangleq exp(-e^x)$$

is quasi-log concave.

Proof Indeed,

$$\begin{array}{r}0<{\int }_0^{\mathrm{\infty }}p=0.21938393439552026\dots <\mathrm{\infty },\\ \phi (x)=e^x,\underset{x\to \mathrm{\infty }}{lim}\phi (x)=\underset{x\to \mathrm{\infty }}{lim}{e}^x=\mathrm{\infty },\end{array}$$

and

$$\underset{x\to \mathrm{\infty }}{lim}\frac{{\phi }^{\prime }(x)}{e^{\phi (x)}}=\underset{x\to \mathrm{\infty }}{lim}\frac{{[{\phi }^{\prime }(x)]}^2}{{\phi }^{″}(x)e^{\phi (x)}}=\underset{x\to \mathrm{\infty }}{lim}\frac{e^x}{exp(e^x)}=0,$$

hence equations in (2.48) hold. Since

$${\phi }^{″}(x)=e^x>0,\mathrm{\forall }x\in (0,\mathrm{\infty }),$$

and

$$2{[{\phi }^{″}(x)]}^3-{\phi }^{(4)}(x){\phi }^{″}(x)+{[{\phi }^{‴}(x)]}^2=2e^{3x}>0,\mathrm{\forall }x\in (0,\mathrm{\infty }),$$

inequalities in (2.27) hold. By Theorem 2.5, the function p is quasi-log concave. This ends the proof. □

In the next section, we demonstrate the applications of Theorem 2.3 and Theorem 2.5 in the theory of k-normal distribution.

4 Quasi-log concavity of pdf of k-normal distribution

The normal distribution (see [14–16]) is considered as the most prominent probability distribution in statistics. Besides the important central limit theorem that says the mean of a large number of random variables drawn from a common distribution, under mild conditions, is distributed approximately normally, the normal distribution is also tractable in the sense that a large number of related results can be derived explicitly and that many qualitative properties may be stated in terms of various inequalities.

But perhaps one of the main practical uses of the normal distribution is to model empirical distributions of many different random variables encountered in practice. In such a case, a possible generalization would be families of distributions having more than two parameters (namely the mean and the standard variation) which may be used to fit empirical distributions more accurately. Examples of such generalizations are the normal-exponential-gamma distribution which contains three parameters and the Pearson distribution which contains four parameters for simulating different skewness and kurtosis values.

In this section, we first introduce another generalization of the normal distribution as follows: If the probability density function of the random variable X is

$$p(x;\mu ,\sigma ,k)\triangleq \frac{k^{1-k^{-1}}}{2\mathrm{\Gamma }(k^{-1})\sigma }exp(-\frac{|x-\mu {|}^k}{k{\sigma }^k}),$$

(4.1)

then we say that the random variable X follows the k-normal distribution or generalized normal distribution (see [17] or [18]), denoted by $X\sim N_k(\mu ,\sigma )$, where

$$x\in (-\mathrm{\infty },\mathrm{\infty }),\mu \in (-\mathrm{\infty },\mathrm{\infty }),\sigma \in (0,\mathrm{\infty }),k\in (1,\mathrm{\infty }),$$

and $\mathrm{\Gamma }(s)$ is the well-known gamma function.

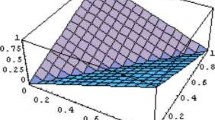
For the probability density function $p(x;\mu ,\sigma ,k)$ of k-normal distribution, the graphs of the functions $p(x;0,1,3/2)$, $p(x;0,1,2)$ and $p(x;0,1,5/2)$ are depicted in Figure 1 and $p(x;0,1,k)$ is depicted in Figure 2.

Figure 1

The graphs of the functions $\mathit{p}\mathbf{(}\mathit{x}\mathbf{;}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{3}\mathbf{/}\mathbf{2}\mathbf{)}$ , $\mathit{p}\mathbf{(}\mathit{x}\mathbf{;}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{)}$ and $\mathit{p}\mathbf{(}\mathit{x}\mathbf{;}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{,}\mathbf{5}\mathbf{/}\mathbf{2}\mathbf{)}$ , where $\mathbf{-}\mathbf{4}\mathbf{⩽}\mathit{x}\mathbf{⩽}\mathbf{4}$ .

Figure 2

The graph of the function $\mathit{p}\mathbf{(}\mathit{x}\mathbf{;}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{,}\mathit{k}\mathbf{)}$ , where $\mathbf{-}\mathbf{4}\mathbf{⩽}\mathit{x}\mathbf{⩽}\mathbf{4}$ , $\mathbf{1}\mathbf{<}\mathit{k}\mathbf{⩽}\mathbf{3}$ .

Clearly, when $k=2$, $p(x;\mu ,\sigma ,k)$ is just the standard normal distribution $N(\mu ,\sigma )$ with mean μ and standard deviation σ, and it is easily checked that $p(x;0,1,k)$ is symmetric about 0 and that

$$p(x;0,1,k)=\sigma p(\sigma x+\mu ;\mu ,\sigma ,k),\mathrm{\forall }x\in (-\mathrm{\infty },\mathrm{\infty }).$$

(4.2)

According to (4.1), we get (see (2) in [17])

$$p(x;\mu ,\frac{\sigma }{s^{1/s}},s)=\frac{s}{2\sigma \mathrm{\Gamma }(1/s)}exp(-|\frac{x-\mu }{\sigma }{|}^s).$$

(4.3)

According to the results of [17], we may easily show that (see [17], p.688)

$$p(x;\mu ,\sigma ,k)>0,{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p(x;\mu ,\sigma ,k)\mathrm{d}t=1,$$

(4.4)

$$\mathrm{E}X=\mu ,$$

(4.5)

$$\mathrm{E}|X-\mathrm{E}X{|}^k={\sigma }^k,$$

(4.6)

and

$$\mathrm{E}{(X-\mathrm{E}X)}^2=\frac{k^{2k^{-1}}\mathrm{\Gamma }(3k^{-1})}{\mathrm{\Gamma }(k^{-1})}{\sigma }^2\{\begin{array}{cc}>{\sigma }^2,\hfill & 1<k<2,\hfill \\ ={\sigma }^2,\hfill & k=2,\hfill \\ <{\sigma }^2,\hfill & k>2.\hfill \end{array}$$

(4.7)

Here μ, ${\sigma }^k$ and σ are the mathematical expectation, k-order absolute central moment and k-order mean absolute central moment of the random variable X, respectively.

We remark here if

$$p_0(x)=exp[-\frac{{(x-\mu )}^k}{k{\sigma }^k}],x\in (\mu ,\mathrm{\infty }),$$

then

$$w(x)\triangleq -p_0^{\prime }(x)=\frac{{(x-\mu )}^{k-1}}{{\sigma }^k}exp[-\frac{{(x-\mu )}^k}{k{\sigma }^k}]>0,$$

and

$${\int }_{\mu }^{\mathrm{\infty }}w(x)\mathrm{d}x=1,$$

where $w(x)$ is the probability density function of a Weibull distribution. Therefore, there are close relationships between the k-normal distribution and the Weibull distribution.

Next, we study the quasi-log concavity of the probability density function of k-normal distribution.

Theorem 4.1 The probability density function $p(x;\mu ,\sigma ,k)$ of the k-normal distribution is quasi-log concave on $(-\mathrm{\infty },\mathrm{\infty })$ for all $\mu \in (-\mathrm{\infty },\mathrm{\infty })$, $\sigma \in (0,\mathrm{\infty })$ and $k\in (1,\mathrm{\infty })$.

Proof In view of (4.2), we may assume that

$$(\mu ,\sigma )=(0,1).$$

Let for convenience that

$$p(x)\triangleq p(x;0,1,k)=cexp[-\phi (x)],$$

where

$$c=\frac{k^{1-k^{-1}}}{2\mathrm{\Gamma }(k^{-1})}>0,\phi (x)=\frac{|x{|}^k}{k}.$$

Then

$$\begin{array}{r}{G}_p[a,a]=0=G_p[b,b],\\ G_p[a,b]=G_p[b,a]\text{and}{G}_p[a,b]=G_p[-b,-a],\end{array}$$

(4.8)

where the last equality holds because p is even.

Now we show that

$$G_p[a,b]⩽0,\mathrm{\forall }a,b\in (-\mathrm{\infty },\mathrm{\infty })$$

(4.9)

in two steps (A) and (B).

• (A) We first consider the case where $k⩾2$.

By (4.8) and continuity, without loss of generality, we may assume that either

$$\text{(i):}0<a<b,\text{or}\text{(ii):}a<0<b.$$

We first consider the case (i): $0<a<b$.

By (4.4), we have

$${\int }_0^{\mathrm{\infty }}p=\frac{1}{2}<\mathrm{\infty }.$$

Since

$$\underset{x\to \mathrm{\infty }}{lim}\phi (x)=\underset{x\to \mathrm{\infty }}{lim}{x}^{k-1}=\mathrm{\infty },\underset{x\to \mathrm{\infty }}{lim}\frac{{\phi }^{\prime }(x)}{e^{\phi (x)}}=\underset{x\to \mathrm{\infty }}{lim}\frac{x^{k-1}}{exp(\frac{x^k}{k})}=0,$$

and

$$\underset{x\to \mathrm{\infty }}{lim}\frac{{[{\phi }^{\prime }(x)]}^2}{{\phi }^{″}(x)e^{\phi (x)}}=\underset{x\to \mathrm{\infty }}{lim}\frac{x^{2k-2}}{(k-1)x^{k-2}exp(\frac{x^k}{k})}=0,$$

equations in (2.48) hold. Since

$${\phi }^{″}(x)=(k-1)x^{k-2}>0,\mathrm{\forall }x\in (0,\mathrm{\infty }),$$

and

$$\begin{array}{r}2{[{\phi }^{″}(x)]}^3-{\phi }^{(4)}(x){\phi }^{″}(x)+{[{\phi }^{‴}(x)]}^2\\ =2{(k-1)}^2{x}^{3k-6}-{(k-1)}^2(k-2)(k-3)x^{2k-6}+{(k-1)}^2{(k-2)}^2{x}^{2k-6}\\ ={(k-1)}^2{x}^{3k-6}+{(k-1)}^2(k-2)x^{2k-6}\\ >0,\mathrm{\forall }x\in (0,\mathrm{\infty }),\end{array}$$

inequalities in (2.27) hold. By Theorem 2.5, inequality (4.9) holds.

Next, we consider the case (ii): $a<0<b$.

Since

$$p^{\prime }(b)<0<p^{\prime }(a),$$

we have

$$G_p[a,b]=\left({\int }_a^{b}p\right)[p^{\prime }(b)-p^{\prime }(a)]-{\left({\int }_a^b{p}^{\prime }\right)}^2⩽\left({\int }_a^{b}p\right)[p^{\prime }(b)-p^{\prime }(a)]<0,$$

that is, inequality (4.9) still holds.

• (B) Next we assume that $1<k<2$.

Since

$${\phi }^{″}(x)=(k-1)x^{k-2}>0,\mathrm{\forall }x\in (0,\mathrm{\infty }),$$

and

$$2{\phi }^{\prime }(x){\phi }^{″}(x)-{\phi }^{‴}(x)=2(k-1)x^{2k-3}+(k-1)(2-k)x^{k-3}⩾0,\mathrm{\forall }x\in (0,\mathrm{\infty }),$$

inequalities in (2.16) hold. By Theorem 2.3, inequality (4.9) holds.

Based on the above analysis, inequality (4.9) is proved.

The proof of Theorem 4.1 is completed. □

In the next section, we demonstrate the applications of Theorem 4.1 in the generalized hierarchical teaching model and the generalized traditional teaching model.

5 Applications in statistics

5.1 Hierarchical teaching model and truncated random variable

We first introduce the hierarchical teaching model as follows.

The usual teaching model assumes that the math scores of each student in a class are treated as a continuous random variable, written as ${\xi }_I$, which takes on some value in the real interval $I=[a_0,a_m]$, and its probability density function $p_I:I\to (0,\mathrm{\infty })$ is continuous. Suppose we now divide the students into m classes, written as

$$Class[a_0,a_1],Class[a_1,a_2],\dots ,Class[a_{m-1},a_m],$$

where

$$0⩽a_0⩽a_1⩽\cdots ⩽a_m,m⩾2,$$

and

$$a_i,a_{i+1},i=0,1,\dots ,m-1,$$

are the lowest and the highest allowable scores of the students of $Class[a_i,a_{i+1}]$, respectively. We introduce a set

$$HTM\{a_0,\dots ,a_m,p_I\}\triangleq \{Class[a_0,a_1],Class[a_1,a_2],\dots ,Class[a_{m-1},a_m],p_I\}$$

called a hierarchical teaching model (see [19–22]) such that the traditional teaching model, denoted by $HTM\{a_0,a_m,p_I\}$, is just a special $HTM\{a_0,\dots ,a_m,p_I\}$, where $m=1$.

If $a_0=-\mathrm{\infty }$ and $a_m=\mathrm{\infty }$, then $HTM\{-\mathrm{\infty },\dots ,\mathrm{\infty },p_I\}$ and $HTM\{-\mathrm{\infty },\mathrm{\infty },p_I\}$ are called generalized hierarchical teaching model and generalized traditional teaching model, respectively.

In order to study the hierarchical teaching model and the traditional teaching model from the angle of the analysis of variance, we need to recall the definition of truncated random variable.

Definition 5.1 Let ${\xi }_I\in I$ be a continuous random variable with continuous probability density function $p_I:I\to (0,\mathrm{\infty })$. If ${\xi }_J\in J\subseteq I$ is also a continuous random variable and its probability density function is

$$p_J:J\to (0,\mathrm{\infty }),p_J(t)\triangleq \frac{p_I(t)}{{\int }_J{p}_I},$$

then we call the random variable ${\xi }_J$ a truncated random variable of the random variable ${\xi }_I$, written as ${\xi }_J\subseteq {\xi }_I$. If ${\xi }_J\subseteq {\xi }_I$ and $J\subset I$, then we call the random variable ${\xi }_J$ a proper truncated random variable of the random variable ${\xi }_I$, written as ${\xi }_J\subset {\xi }_I$. Here I and J are high dimensional intervals.

We point out that a basic property of the truncated random variable is as follows: Let ${\xi }_I\in I$ be a continuous random variable with continuous probability density function $p_I:I\to (0,\mathrm{\infty })$. If

$${\xi }_{I_{\ast }}\subseteq {\xi }_I,{\xi }_{I^{\ast }}\subseteq {\xi }_I\text{and}{I}_{\ast }\subseteq I^{\ast },$$

then ${\xi }_{I_{\ast }}\subseteq {\xi }_{I^{\ast }}$. If

$${\xi }_{I_{\ast }}\subseteq {\xi }_I,{\xi }_{I^{\ast }}\subseteq {\xi }_I\text{and}{I}_{\ast }\subset I^{\ast },$$

then ${\xi }_{I_{\ast }}\subset {\xi }_{I^{\ast }}$.

Indeed, by Definition 5.1, the probability density functions of the truncated random variables ${\xi }_{I_{\ast }}$, ${\xi }_{I^{\ast }}$ are

$$\begin{array}{r}{p}_{I_{\ast }}:I_{\ast }\to (0,\mathrm{\infty }),p_{I_{\ast }}(t)=\frac{p_I(t)}{{\int }_{I_{\ast }}{p}_I},\\ p_{I^{\ast }}:I^{\ast }\to (0,\mathrm{\infty }),p_{I^{\ast }}(t)=\frac{p_I(t)}{{\int }_{I^{\ast }}{p}_I},\end{array}$$

respectively. Thus, the probability density function of ${\xi }_{I_{\ast }}$ can be rewritten as

$$p_{I_{\ast }}:I_{\ast }\to (0,\mathrm{\infty }),p_{I_{\ast }}(t)=\frac{p_I(t)/{\int }_{I^{\ast }}{p}_I}{{\int }_{I_{\ast }}(p_I/{\int }_{I^{\ast }}{p}_I)}=\frac{p_{I^{\ast }}(t)}{{\int }_{I_{\ast }}{p}_{I^{\ast }}}.$$

Hence

$$I_{\ast }\subseteq I^{\ast }\Rightarrow {\xi }_{I_{\ast }}\subseteq {\xi }_{I^{\ast }}\text{and}{I}_{\ast }\subset I^{\ast }\Rightarrow {\xi }_{I_{\ast }}\subset {\xi }_{I^{\ast }}.$$

According to the definitions of the mathematical expectation $\mathrm{E}\phi ({\xi }_J)$ and the variance $Var\phi ({\xi }_J)$ with Definition 5.1, we easily get

$$\mathrm{E}\phi ({\xi }_J)\triangleq {\int }_J{p}_J\phi =\frac{{\int }_J{p}_I\phi }{{\int }_J{p}_I},$$

(5.1)

and

$$Var\phi ({\xi }_J)\triangleq \mathrm{E}{[\phi ({\xi }_J)-\mathrm{E}\phi ({\xi }_J)]}^2=\frac{{\int }_J{p}_I{\phi }^2}{{\int }_J{p}_I}-{\left(\frac{{\int }_J{p}_I\phi }{{\int }_J{p}_I}\right)}^2,$$

(5.2)

where ${\xi }_J\subseteq {\xi }_I$, and the function $\phi :J\to (-\mathrm{\infty },\mathrm{\infty })$ of the random variable ${\xi }_J$ is continuous.

In the generalized hierarchical teaching model $HTM\{-\mathrm{\infty },\dots ,\mathrm{\infty },p_I\}$, the math scores of each student in $Class[a_i,a_{i+1}]$ is also a random variable, written as ${\xi }_{[a_i,a_{i+1}]}$. Since

$$[a_i,a_{i+1}]\subseteq I,i=0,1,\dots ,m-1,$$

so ${\xi }_{[a_i,a_{i+1}]}$ is a truncated random variable of the random variable ${\xi }_I$. Assume that the $j-i$ classes, i.e.,

$$Class[a_i,a_{i+1}],Class[a_{i+1},a_{i+2}],\dots ,Class[a_{j-1},a_j]$$

are merged into one, written as $Class[a_i,a_j]$. Since $[a_i,a_j]\subseteq I$, we know that ${\xi }_{[a_i,a_j]}$ is a truncated random variable of the random variable ${\xi }_I$, where $0⩽i<j⩽m$. In general, we have

$${\xi }_{[a_i,a_j]}\subseteq {\xi }_{[a_{i^{\prime }},a_{j^{\prime }}]}\subseteq {\xi }_I,\mathrm{\forall }{i}^{\prime },i,j,j^{\prime }:0⩽i^{\prime }⩽i<j⩽j^{\prime }⩽m.$$

(5.3)

In the generalized hierarchical teaching model $HTM\{-\mathrm{\infty },\dots ,\mathrm{\infty },p_I\}$, we are concerned with the relationship between the variance $Var{\xi }_{[a_i,a_j]}$ and the variance $Var{\xi }_I$, where $0⩽i<j⩽m$, so as to decide the superiority and inferiority of the hierarchical and the traditional teaching models.

If

$$Var{\xi }_{[a_i,a_j]}⩽Var{\xi }_I,\mathrm{\forall }i,j:0⩽i<j⩽m,$$

(5.4)

then in view of the usual meaning of the variance, we tend to think that this generalized hierarchical teaching model is better than the generalized traditional teaching model. Otherwise, this generalized hierarchical teaching model is probably not worth promoting, where $I=(-\mathrm{\infty },\mathrm{\infty })$.

In this section, one of our purposes is to study the generalized hierarchical teaching model and the generalized traditional teaching model from the angle of the analysis of variance so as to decide the superiority and inferiority of the generalized hierarchical and the generalized traditional teaching models. In particular, we will study the conditions such that inequality (5.4) holds (see Theorem 5.2).

In the generalized hierarchical teaching model $HTM\{-\mathrm{\infty },\dots ,\mathrm{\infty },p_I\}$, we can choose the parameters $a_1,a_2,\dots ,a_{m-1}\in (-\mathrm{\infty },\mathrm{\infty })$ such that the ‘variance’

$$\begin{array}{r}Var(Var{\xi }_{[a_0,a_1]},\dots ,Var{\xi }_{[a_{m-1},a_m]})\\ \triangleq \frac{1}{m}\sum _{j=0}^{m-1}{(Var{\xi }_{[a_j,a_{j+1}]}-\frac{1}{m}\sum _{i=0}^{m-1}Var{\xi }_{[a_i,a_{i+1}]})}^2\end{array}$$

(5.5)

of

$$Var{\xi }_{[a_0,a_1]},Var{\xi }_{[a_1,a_2]},\dots ,Var{\xi }_{[a_{m-1},a_m]}$$

is the minimal by means of mathematical software, its purpose is to make the scores of the classes

$$Class[a_0,a_1],Class[a_1,a_2],\dots ,Class[a_{m-1},a_m]$$

stable, where $a_0=-\mathrm{\infty }$ and $a_m=\mathrm{\infty }$.

Remark 5.1 We remark here if ${\xi }_I\in I$ is a continuous random variable with continuous probability density function $p_I:I\to (0,\mathrm{\infty })$, then the integration ${\int }_I{p}_I$ converges (see [23]), and it satisfies the following conditions:

$${\int }_I{p}_I=1,P_I(x)\triangleq P({\xi }_I<x)={\int }_{(-\mathrm{\infty },x)\cap I}{p}_I,\mathrm{\forall }x\in I.$$

(5.6)

We call the function $P_I:I\to [0,1]$ a probability distribution function of the random variable ${\xi }_I$, where $P_I(x)$ is the probability of the random event ‘${\xi }_I<x$’, and I is an interval.

5.2 Applications in the analysis of variance

The analysis of variance is one of the central topics in statistics. Recently, the authors [24] have expanded the connotation of analysis of variance and obtained some interesting results.

In this section, we point out the significance of quasi-log concavity in the analysis of variance as follows.

Theorem 5.1 Let ${\xi }_I$ be a continuous random variable and its probability density function $p_I:I\to (0,\mathrm{\infty })$ be twice continuously differentiable. Then the function $p_I:I\to (0,\mathrm{\infty })$ is quasi-log concave if and only if

$$0⩽Var[{(log{p}_I)}^{\prime }({\xi }_{[a,b]})]⩽-\mathrm{E}[{(log{p}_I)}^{″}({\xi }_{[a,b]})],\mathrm{\forall }a,b\in I,a<b,$$

(5.7)

where ${\xi }_{[a,b]}\in [a,b]$ is a truncated random variable of the random variable ${\xi }_I$.

Proof By identities (2.6) and (5.1) with (5.2), we get

$$\begin{array}{r}Var[{(log{p}_I)}^{\prime }({\xi }_{[a,b]})]+\mathrm{E}[{(log{p}_I)}^{″}({\xi }_{[a,b]})]\\ =Var\left(\frac{p_I^{\prime }}{p_I}\right)+\mathrm{E}\left[\frac{p_I{p}_I^{\prime \prime }-{(p_I^{\prime })}^2}{p_I^2}\right]\\ =\frac{{\int }_a^b{(\frac{p_I^{\prime }}{p_I})}^2{p}_I}{{\int }_a^b{p}_I}-{\left(\frac{{\int }_a^b\frac{p_I^{\prime }}{p_I}{p}_I}{{\int }_a^b{p}_I}\right)}^2+\frac{{\int }_a^b\frac{p_I{p}_I^{\prime \prime }-{(p_I^{\prime })}^2}{p_I^2}{p}_I}{{\int }_a^b{p}_I}\\ =\frac{{\int }_a^b{p}_I^{\prime \prime }}{{\int }_a^b{p}_I}-{\left(\frac{{\int }_a^b{p_I}^{\prime }}{{\int }_a^b{p}_I}\right)}^2\\ =\frac{{\int }_a^b{p}_I{\int }_a^b{p}_I^{\prime \prime }-{({\int }_a^b{p}_I^{\prime })}^2}{{({\int }_a^b{p}_I)}^2},\end{array}$$

i.e.,

$$Var[{(log{p}_I)}^{\prime }({\xi }_{[a,b]})]+\mathrm{E}[{(log{p}_I)}^{″}({\xi }_{[a,b]})]=\frac{{\int }_a^b{p}_I{\int }_a^b{p}_I^{\prime \prime }-{({\int }_a^b{p}_I^{\prime })}^2}{{({\int }_a^b{p}_I)}^2}.$$

(5.8)

According to identity (5.8), we know that inequality (1.6) can be rewritten as (5.7).

This completes the proof of Theorem 5.1. □

Remark 5.2 According to Theorem 5.1, quasi-log concavity is of great significance in the analysis of variance.

5.3 Applications in the generalized hierarchical teaching model

Now we demonstrate the application of Theorem 4.1 in the generalized hierarchical teaching model.

In the generalized hierarchical teaching model $HTM\{-\mathrm{\infty },\dots ,\mathrm{\infty },p_I\}$, the math scores of each student are treated as a random variable ${\xi }_I$, where ${\xi }_I\in I=(-\mathrm{\infty },\mathrm{\infty })$. By using the central limit theorem (see [25]), we may think that the random variable ${\xi }_I$ follows a normal distribution, that is, ${\xi }_I\sim N_2(\mu ,\sigma )$, where μ is the average score of the students and σ is the mean square deviation of the score. Hence

$$p_I(x)=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{{(x-\mu )}^2}{2{\sigma }^2}],\mathrm{\forall }x\in I.$$

(5.9)

We remark here that if the math scores ${\xi }_I$ of each student satisfies

$${\xi }_I\in [0,1]\text{and}\mu \in [0,1],$$

then, by (5.9), we have

$$P({\xi }_I<0)\approx 0,P({\xi }_I>1)\approx 0.$$

Hence we can use the generalized hierarchical teaching model instead of the hierarchical teaching model, approximately.

Based on the above analysis and Theorem 4.1, we have the following theorem.

Theorem 5.2 In the generalized hierarchical teaching model $HTM\{-\mathrm{\infty },\dots ,\mathrm{\infty },p_I\}$, assume that ${\xi }_I\sim N_2(\mu ,\sigma )$. Then we have the following inequality:

$$Var{\xi }_{[a_i,a_j]}⩽Var{\xi }_I={\sigma }^2,\mathrm{\forall }i,j:0⩽i<j⩽m.$$

(5.10)

Proof Note that

$$p_I(t)=p(t;\mu ,\sigma ,2)$$

is quasi-log concave by Theorem 4.1, hence inequality (5.7) holds by Theorem 5.1, so we obtain that

$$Var[{(log{p}_I)}^{\prime }({\xi }_{[a_i,a_j]})]⩽-\mathrm{E}[{(log{p}_I)}^{″}({\xi }_{[a_i,a_j]})].$$

(5.11)

Note that

$$\begin{array}{c}Var(\phi +C)\equiv Var(\phi ),Var(C\phi )\equiv C^{2}Var(\phi ),\mathrm{E}(C\phi )\equiv C\mathrm{E}(\phi ),\hfill \\ {(log{p}_I)}^{\prime }({\xi }_{[a_i,a_j]})=-\frac{{\xi }_{[a_i,a_j]}-\mu }{{\sigma }^2},{(log{p}_I)}^{″}({\xi }_{[a_i,a_j]})=-\frac{1}{{\sigma }^2},\mathrm{E}(1)=1,\hfill \end{array}$$

where C is a constant. By (5.11), we have

$$\begin{array}{r}Var(-\frac{{\xi }_{[a_i,a_j]}-\mu }{{\sigma }^2})⩽-\mathrm{E}(-\frac{1}{{\sigma }^2})\\ \iff \frac{1}{{\sigma }^4}Var{\xi }_{[a_i,a_j]}⩽\frac{1}{{\sigma }^2}\mathrm{E}(1)\iff Var{\xi }_{[a_i,a_j]}⩽Var{\xi }_I={\sigma }^2,\end{array}$$

that is to say, inequality (5.10) holds.

This completes the proof of Theorem 5.2. □

Remark 5.3 According to Theorem 5.2, we may conclude that the generalized hierarchical teaching model is normally better than the generalized traditional teaching model.

5.4 Applications in the generalized traditional teaching model

Next, we demonstrate the applications of Theorem 4.1 in the generalized traditional teaching model as follows.

In the generalized traditional teaching model $HTM\{-\mathrm{\infty },\mathrm{\infty },p_I\}$, the math scores of each student are treated as a random variable ${\xi }_I$, where ${\xi }_I\in I=(-\mathrm{\infty },\mathrm{\infty })$. By using the central limit theorem (see [25]), we may think that the random variable ξ follows a normal distribution, that is, ${\xi }_I\sim N_2(\mu ,\sigma )$, where μ is the average score of the students and σ is the mean square deviation of the score. If the top and bottom students are insignificant, that is to say, the variance $Var{\xi }_I$ of the random variable ${\xi }_I$ is close to 0, according to Figure 1 and Figure 2 with formula (4.7), we may think that there is a real number $k\in (2,\mathrm{\infty })$ such that ${\xi }_I\sim N_k(\mu ,\sigma )$. Otherwise, we may think that there is a real number $k\in (1,2)$ such that ${\xi }_I\sim N_k(\mu ,\sigma )$. We can estimate the number k by means of a sampling procedure.

In the generalized traditional teaching model $HTM\{-\mathrm{\infty },\mathrm{\infty },p_I\}$, we may assume that

$${\xi }_J\subset {\xi }_I,{\xi }_I\sim N_k(\mu ,\sigma ),k>1,$$

where $J=(\mu ,\mathrm{\infty })$, and $\mu \in (0,\mathrm{\infty })$ is the average math score of the students and σ is the k-order mean absolute central moment of the score. Then the probability density function of ${\xi }_J$ is that

$$p_J(t)=\frac{p(x;\mu ,\sigma ,k)}{{\int }_{J}p(x;\mu ,\sigma ,k)},\mathrm{\forall }x\in J.$$

In the generalized traditional teaching model $HTM\{-\mathrm{\infty },\mathrm{\infty },p_I\}$, suppose that the math score of the student is ${\xi }_J$. In order to stimulate the learning enthusiasm of students, we may want to give each student a bonus payment $\mathcal{A}({\xi }_J)$. The function

$$\mathcal{A}:J\to (0,\mathrm{\infty })$$

may be regarded as an allowance function.

In the generalized traditional teaching model $HTM\{-\mathrm{\infty },\mathrm{\infty },p_I\}$, we define the allowance function as follows:

$$\mathcal{A}:J\to (0,\mathrm{\infty }),\mathcal{A}(x)\triangleq c{(x-\mu )}^{k-1},c>0,k>1.$$

(5.12)

For the above allowance function (5.12), we have the following theorem.

Theorem 5.3 In the generalized traditional teaching model $HTM\{-\mathrm{\infty },\mathrm{\infty },p_I\}$, assume that

$${\xi }_J\subset {\xi }_I,{\xi }_I\sim N_k(\mu ,\sigma ),k>1.$$

Then we have the following inequalities:

$$0⩽Var[\mathcal{A}({\xi }_{[a,b]})]⩽c{\sigma }^k\mathrm{E}[{\mathcal{A}}^{\prime }({\xi }_{[a,b]})],\mathrm{\forall }a,b\in J,a<b.$$

(5.13)

Here the allowance function $\mathbb{A}$ is defined by (5.12).

Proof By Theorem 4.1, the function $p\triangleq p_J(t)$ is quasi-log concave on J. Hence inequalities (5.7) hold by Theorem 5.1. Note that

$$\begin{array}{c}Var(C\mathcal{A})\equiv C^{2}Var(\mathcal{A}),\mathrm{E}(C\mathcal{A})\equiv C\mathrm{E}(\mathcal{A}),\hfill \\ {(log{p}_I)}^{\prime }({\xi }_{[a,b]})=-\frac{{({\xi }_{[a,b]}-\mu )}^{k-1}}{{\sigma }^k}=-\frac{1}{c{\sigma }^k}\mathcal{A}({\xi }_{[a,b]}),\hfill \end{array}$$

and

$${(log{p}_I)}^{″}({\xi }_{[a,b]})=-\frac{1}{c{\sigma }^k}{\mathcal{A}}^{\prime }({\xi }_{[a,b]}),$$

where C is a constant. By inequalities (5.7), we get

$$\begin{array}{c}Var[{(log{p}_I)}^{\prime }({\xi }_{[a,b]})]⩽-\mathrm{E}[{(log{p}_I)}^{″}({\xi }_{[a,b]})],\hfill \\ Var[-\frac{1}{c{\sigma }^k}\mathcal{A}({\xi }_{[a,b]})]⩽-\mathrm{E}[-\frac{1}{c{\sigma }^k}{\mathcal{A}}^{\prime }({\xi }_{[a,b]})],\hfill \end{array}$$

and

$$\frac{1}{{(c{\sigma }^k)}^2}Var[\mathcal{A}({\xi }_{[a,b]})]⩽\frac{1}{c{\sigma }^k}\mathrm{E}[{\mathcal{A}}^{\prime }({\xi }_{[a,b]})].$$

That is to say, inequalities (5.13) hold.

This completes the proof of Theorem 5.3. □

Remark 5.4 A large number of inequality analysis and statistical theories are used in this paper. Some theories in the proofs of our results are used in the references [5, 23, 24, 26–34].