Retracted Article: Jacobi spectral solution for integral algebraic equations of index 1

Abstract

This paper is concerned with obtaining the approximate solution of a class of semi-explicit integral algebraic equations (IAEs) of index 1. A Jacobi collocation method is proposed for the IAEs of index 1. A rigorous analysis of the error bound in weighted $L^2$-norm is also provided, which theoretically justifies the spectral rate of convergence while the kernels and the source functions are sufficiently smooth. The results of several numerical experiments are presented which support the theoretical results.

MSC:65R20, 45F15.

1 Introduction

Consider the following system of integral equations:

$$\{\begin{array}{l}y(t)=f_1(t)+{\int }_0^t{K}_{11}(t,s)y(s)ds+{\int }_0^t{K}_{12}(t,s)z(s)ds,\\ 0=f_2(t)+{\int }_0^t{K}_{21}(t,s)y(s)ds+{\int }_0^t{K}_{22}(t,s)z(s)ds,t\in I=[0,T],\end{array}$$

(1.1)

where $K_{ij}(\cdot ,\cdot )$, $i,j=1,2$ are $d_i\times d_j$ matrices, $f_1$, $f_2$ are given $d_1$, $d_2$ dimensional vector functions, and $(y(t),z(t))$ is a solution to be determined. Here, we assume that the data functions $f_i$, $K_{ij}$ ($i,j=1,2$) are sufficiently smooth such that $f_2(0)=0$ and $|det(K_{22}(t,t))|\ge k_0>0$ for all $t\in I$. The existence and uniqueness results for the solution of the system (1.1) have been discussed in [1].

The system (1.1) is a particular case of the general form of the integral algebraic equations (IAEs)

$$A(t)X(t)=G(t)+{\int }_0^{t}K(t,s,X(s))ds$$

which has been introduced in [1], where $det(A(t))=0$, $Rank(A)\ge 1$. An initial investigation of these equations indicates that they have properties very similar to differential algebraic equations (DAEs). In analogy with the theory of DAEs (see, e.g., [2]), Kauthen [3] in 2000 has called the system (1.1) the semi-explicit IAEs of index 1.

Coupled systems of integral algebraic equations (IAEs) consisting of the first and second kind Volterra integral equations (VIEs) arise in many mathematical modeling processes, e.g., the controlled heat equation which represents a boundary reaction in diffusion of chemicals [4], the two dimensional biharmonic equation in a semi-infinite strip [5, 6], dynamic processes in chemical reactors [7], and the deformed Pohlmeyer equation [8]. Also a good source of information (including numerous additional references) on applications of IAEs system is the monograph by Brunner [1].

As far as we know, there have been a few works available in the literature which has considered the theory of IAEs system. The existence and uniqueness results of continuous solution to linear IAEs system have been investigated by Chistyakov [9]. Gear in [10] defined the index notion of IAEs system by considering the effect of perturbation of the equations on the solutions. He has also introduced the index reduction procedure for IAEs system in [10]. Bulatov and Chistyakov [11] gave the existence and uniqueness conditions of the solution for IAEs systems with convolution kernels and defined the index notion in analogy to Gear’s approach. Further details of their investigation may be found in [12, 13]. Kauthen in [3] analyzed the spline collocation method and its convergence properties for the semi-explicit IAEs system (1.1). Brunner [1] defined the index-1 tractability for the IAEs system (1.1) and he also investigated the existence of a unique solution for this type of systems. Recently, the authors in [4] have defined the index-2 tractability for a class of IAEs and presented the Jacobi collocation method including the matrix-vector multiplication representation of the equation and its convergence analysis. The authors in [14] proposed the Legendre collocation method for IAEs of index 1 and obtained the posteriori error estimation.

It is well known that the classical Jacobi polynomials have been used extensively in mathematical analysis and practical applications, and play an important role in the analysis and implementation of the spectral methods. The main purpose of this work is to use the Jacobi collocation method to numerically solve the IAEs (1.1). We will provide a posteriori error estimate in the weighted $L^2$-norm which theoretically justifies the spectral rate of convergence. To do so, we use some well-known results of the approximation theory from [15–17] including the Jacobi polynomials, the Gronwall inequality and the Lebesgue constant for the Lagrange interpolation polynomials.

This paper is organized as follows. In Section 2, we carry out the Jacobi collocation approach for the IAEs system (1.1). A posteriori error estimation of the method in the weighted $L^2$-norm as a main result of the paper is given in Section 3. Some numerical experiments are reported in Section 4 to verify the theoretical results obtained in Section 3. The final section contains conclusions and remarks.

2 The Jacobi collocation method

This section is devoted to applying the Jacobi collocation method to numerically solve the IAEs system (1.1). We first use some variable transformations to change the equation into a new system of integral equations defined on the standard interval $[-1,1]$, so that the Jacobi orthogonal polynomial theory can be applied conveniently. For simplicity, we will consider the IAEs system (1.1) with $d_1=d_2=1$.

Let ${\omega }^{\alpha ,\beta }(x)={(1-x)}^{\alpha }{(1+x)}^{\beta }$ ($\alpha ,\beta >-1$) be a weight function in the usual sense. As defined in [15, 18, 19], the set of Jacobi polynomials ${\{J_n^{\alpha ,\beta }(x)\}}_{n=0}^{\mathrm{\infty }}$ forms a complete $L_{{\omega }^{\alpha ,\beta }}^2(-1,1)$ orthogonal system, where $L_{{\omega }^{\alpha ,\beta }}^2(-1,1)$ is the space of functions $f:[-1,1]\to \mathbb{R}$ with ${\parallel f\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2(-1,1)}^2<\mathrm{\infty }$, and

$${\parallel f\parallel }_{L_{{\omega }^{\alpha ,\beta }}^2(-1,1)}^2={〈f,f〉}_{L_{{\omega }^{\alpha ,\beta }}^2(-1,1)}={\int }_{-1}^1|f(x){|}^2{\omega }^{\alpha ,\beta }(x)dx.$$

For the sake of applying the theory of orthogonal polynomials, we use the change of variables:

$$\eta =\frac{2}{T}s-1,-1\le \eta \le \tau ,\tau =\frac{2}{T}t-1,-1\le \tau \le 1,$$

(2.1)

to rewrite the IAEs system (1.1) as

$$\{\begin{array}{l}\hat{y}(\tau )={\hat{f}}_1(\tau )+{\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )\hat{y}(\eta )d\eta +{\int }_{-1}^{\tau }{\hat{K}}_{12}(\tau ,\eta )\hat{z}(\eta )d\eta ,\\ 0={\hat{f}}_2(\tau )+{\int }_{-1}^{\tau }{\hat{K}}_{21}(\tau ,\eta )\hat{y}(\eta )d\eta +{\int }_{-1}^{\tau }{\hat{K}}_{22}(\tau ,\eta )\hat{z}(\eta )d\eta ,\end{array}$$

(2.2)

where

$$\begin{array}{c}{\hat{f}}_i(\tau )=f_i(\frac{T}{2}(\tau +1)),{\hat{K}}_{ij}(\tau ,\eta )=\frac{T}{2}{K}_{ij}(\frac{T}{2}(\tau +1),\frac{T}{2}(\eta +1)),i,j=1,2,\hfill \\ \hat{y}(\tau )=y(\frac{T}{2}(\tau +1)),\hat{z}(\tau )=z(\frac{T}{2}(\tau +1)).\hfill \end{array}$$

We consider the discrete expansion of ${\hat{K}}_{ij}(\tau ,\eta )$ as follows:

$$I_N({\hat{K}}_{ij}({\tau }_n,\eta ))=\sum _{k=0}^N{({\hat{K}}_{ij})}_k{J}_k^{\alpha ,\beta }(\eta )(i,j=1,2),$$

(2.3)

where $I_N$ is a projection to the finite dimensional space $B_N=span{\{J_n^{\alpha ,\beta }(x)\}}_{n=0}^N$ and $J_n^{\alpha ,\beta }(x)$ is the Jacobi polynomial such that

$${({\hat{K}}_{ij})}_k=\frac{1}{{\gamma }_k}\sum _{l=0}^N{\omega }_l{\hat{K}}_{ij}({\tau }_n,{\tau }_l)J_k^{\alpha ,\beta }({\tau }_l),$$

(2.4)

where the quadrature points ${\tau }_l$ are the Jacobi Gauss quadrature points, i.e., the zeros of $J_{N+1}^{\alpha ,\beta }(x)$, the normalization constant ${\gamma }_k$ and the weights ${\omega }_l$ are given in [[18], p.231].

In the Jacobi collocation method, we seek a solution of the form

$$I_N(\hat{y}(\eta ))={\hat{y}}_N(\eta )=\sum _{k=0}^N{\hat{y}}_k{J}_k^{\alpha ,\beta }(\eta ),I_N(\hat{z}(\eta ))={\hat{z}}_N(\eta )=\sum _{k=0}^N{\hat{z}}_k{J}_k^{\alpha ,\beta }(\eta ).$$

(2.5)

Inserting the discrete expansions (2.3) and (2.5) into (2.2), we obtain

$$\{\begin{array}{l}{\hat{y}}_N(\tau )={\hat{f}}_1(\tau )+{\sum }_{k=0}^N{\sum }_{l=k}^N(c_{kl}+c_{kl}^{\prime })V_{kl}(\tau ),\\ 0={\hat{f}}_2(\tau )+{\sum }_{k=0}^N{\sum }_{l=k}^N(q_{kl}+q_{kl}^{\prime })V_{kl}(\tau ),\end{array}$$

(2.6)

where $V_{kl}(\tau )={\int }_{-1}^{\tau }{J}_k^{\alpha ,\beta }(\eta )J_l^{\alpha ,\beta }(\eta )d\eta$, and

$$\begin{array}{c}{c}_{kl}=\{\begin{array}{ll}{\hat{y}}_k{({\hat{K}}_{11})}_k,& k=l,\\ {\hat{y}}_k{({\hat{K}}_{11})}_l+{\hat{y}}_l{({\hat{K}}_{11})}_k,& k\ne l,\end{array}{c}_{kl}^{\prime }=\{\begin{array}{ll}{\hat{z}}_k{({\hat{K}}_{12})}_k,& k=l,\\ {\hat{z}}_k{({\hat{K}}_{12})}_l+{\hat{z}}_l{({\hat{K}}_{12})}_k,& k\ne l,\end{array}\hfill \\ q_{kl}=\{\begin{array}{ll}{\hat{y}}_k{({\hat{K}}_{21})}_k,& k=l,\\ {\hat{y}}_k{({\hat{K}}_{21})}_l+{\hat{y}}_l{({\hat{K}}_{21})}_k,& k\ne l,\end{array}{q}_{kl}^{\prime }=\{\begin{array}{ll}{\hat{z}}_k{({\hat{K}}_{22})}_k,& k=l,\\ {\hat{z}}_k{({\hat{K}}_{22})}_l+{\hat{z}}_l{({\hat{K}}_{22})}_k,& k\ne l.\end{array}\hfill \end{array}$$

By substituting the collocation points ${\tau }_n$ in the system (2.6) and employing the discrete representation (2.5), we obtain

$$\{\begin{array}{l}{\hat{y}}_N({\tau }_n)={\hat{f}}_1({\tau }_n)+{\sum }_{k=0}^N{\sum }_{l=k}^N(c_{kl}+c_{kl}^{\prime })V_{kl}({\tau }_n),\\ 0={\hat{f}}_2({\tau }_n)+{\sum }_{k=0}^N{\sum }_{l=k}^N(q_{kl}+q_{kl}^{\prime })V_{kl}({\tau }_n)\end{array}(n=0,1,\dots ,N)$$

(2.7)

and we let

$$\begin{array}{c}J=(J_i^{\alpha ,\beta }({\tau }_j))(i,j=0,1,\dots ,N),Y={({\hat{y}}_0,{\hat{y}}_1,\dots ,{\hat{y}}_N)}^T,Z={({\hat{z}}_0,{\hat{z}}_1,\dots ,{\hat{z}}_N)}^T,\hfill \\ F_1={({\hat{f}}_1({\tau }_0),{\hat{f}}_1({\tau }_1),\dots ,{\hat{f}}_1({\tau }_N))}^T,F_2={({\hat{f}}_2({\tau }_0),{\hat{f}}_2({\tau }_1),\dots ,{\hat{f}}_2({\tau }_N))}^T,\hfill \\ A=(a_{ln}),a_{ln}=\sum _{k=0}^N{({\hat{K}}_{11})}_k{V}_{kl}({\tau }_n),\hfill \\ B=(b_{ln}),b_{ln}=\sum _{k=0}^N{({\hat{K}}_{12})}_k{V}_{kl}({\tau }_n)(l,n=0,1,\dots ,N),\hfill \\ C=(c_{ln}),c_{ln}=\sum _{k=0}^N{({\hat{K}}_{21})}_k{V}_{kl}({\tau }_n),\hfill \\ D=(d_{ln}),d_{ln}=\sum _{k=0}^N{({\hat{K}}_{22})}_k{V}_{kl}({\tau }_n)(l,n=0,1,\dots ,N),\hfill \end{array}$$

then system (2.7) can be rewritten as

$$\left(\begin{array}{cc}A-J& B\\ C& D\end{array}\right)\left(\begin{array}{c}Y\\ Z\end{array}\right)=\left(\begin{array}{c}-F_1\\ -F_2\end{array}\right).$$

(2.8)

Now, the unknown coefficients ${\hat{y}}_k$ and ${\hat{z}}_k$, $k=0,1,\dots ,N$ are obtained by solving the linear system (2.8) and finally the approximate solutions ${\hat{y}}_N(\eta )$ and ${\hat{z}}_N(\eta )$ will be computed by substituting these coefficients into (2.5). Because the matrix of the coefficients of the linear system (2.8) is non-symmetric, when N is large, we can use some basic iterative methods to solve it, such as the generalized minimal residual (GMRES) method (see [[19], pp.48-60]), which is popular for solving non-symmetric linear systems.

3 Error estimation

In this section, we present a posteriori error estimate for the proposed scheme in the weighted $L^2$-norm. Firstly, we recall some preliminaries and useful lemmas from [15].

Let ${\mathrm{P}}_N$ be the space of all polynomials of degree not exceeding N, and $\mathrm{\Lambda }=(-1,1)$. From [15], the inverse inequality concerning differentiability of the algebraic polynomials on the interval can be expressed in terms of $L^p$-norm.

Lemma 3.1 (see [15])

Let $\phi \in {\mathrm{P}}_N$, then for any integer $r\ge 1$, $2\le p\le \mathrm{\infty }$, there exists a positive constant C independent of N such that

$${\parallel {\phi }^{(r)}\parallel }_{L_{{\omega }^{\alpha ,\beta }}^p(\mathrm{\Lambda })}\le C{N}^{2r}{\parallel \phi \parallel }_{L_{{\omega }^{\alpha ,\beta }}^p(\mathrm{\Lambda })}.$$

(3.1)

From now on, to simplify the notation, we denote ${\parallel \cdot \parallel }_{L_{{\omega }^{\alpha ,\beta }}^2(\mathrm{\Lambda })}$ by $\parallel \cdot \parallel$ and $J_k^{\alpha ,\beta }(x)$ by $J_k(x)$. We also give some error bounds for the Jacobi system in terms of the Sobolev norms. The Sobolev norm and semi-norm of order $m\ge 0$, considered in this section, are given by

$${\parallel u(x)\parallel }_{H^m(\mathrm{\Lambda })}={\left(\sum _{k=0}^m\parallel u^{(m)}(x)\parallel \right)}^{\frac{1}{2}},$$

(3.2)

$$|u(x){|}_{H^{m,N}(\mathrm{\Lambda })}={\left(\sum _{j=min\{m,N+1\}}^m\parallel u^{(j)}(x)\parallel \right)}^{\frac{1}{2}}.$$

(3.3)

Lemma 3.2 (see [15])

Let $u\in H^m(\mathrm{\Lambda })$, $I_{N}u={\sum }_{k=0}^N{\hat{u}}_k{J}_k$ is the truncated orthogonal Jacobi series of u. The truncation error $u-I_{N}u$ can be estimated as follows:

$$\parallel u-I_{N}u\parallel \le C{N}^{-m}|u{|}_{H^{m,N}(\mathrm{\Lambda })},\mathrm{\forall }u\in H^m(\mathrm{\Lambda }),$$

(3.4)

$${\parallel u-I_{N}u\parallel }_{H^l(\mathrm{\Lambda })}\le C{N}^{2l-\frac{1}{2}-m}|u{|}_{H^{m,N}(\mathrm{\Lambda })},\mathrm{\forall }u\in H^m(\mathrm{\Lambda }),1\le l\le m.$$

(3.5)

The following main theorem reveals the convergence results of the presented scheme in the weighted $L^2$-norm.

Theorem 3.1 Consider the system of integral algebraic equation (2.2) where $\hat{y},\hat{z}\in H^m(\mathrm{\Lambda })$ and the data functions ${\hat{f}}_i$, ${\hat{K}}_{ij}$, $i,j=1,2$, are sufficiently smooth and $|{\hat{K}}_{22}(\tau ,\tau )|\ge k_0>0$ for all $\tau \in \mathrm{\Lambda }$. Let $({\hat{y}}_N,{\hat{z}}_N)$ be the Jacobi collocation approximation of $(\hat{y},\hat{z})$ which is defined by (2.5). Then the following estimates hold:

$$\begin{array}{c}\parallel {\hat{y}}_N-\hat{y}\parallel \le C{N}^{-m}(|f_1{|}_{H^{m,N}(\mathrm{\Lambda })}+N^{-1}(|\hat{y}{|}_{H^{m,N}(\mathrm{\Lambda })}+|\hat{z}{|}_{H^{m,N}(\mathrm{\Lambda })}))+C{N}^{-1}(\parallel \hat{y}\parallel +\parallel \hat{z}\parallel )\hfill \\ \phantom{\parallel {\hat{y}}_N-\hat{y}\parallel \le }+\{\begin{array}{l}C{N}^{-2m}logN({\mathrm{\Omega }}_{11}|\hat{y}|+{\mathrm{\Omega }}_{12}|\hat{z}|)\\ +C{N}^{-m}logN({\mathrm{\Omega }}_{11}\parallel \hat{y}\parallel +{\mathrm{\Omega }}_{12}\parallel \hat{z}\parallel ),& -1<\alpha ,\beta \le -\frac{1}{2},\\ C{N}^{\frac{1}{2}+\gamma -2m}({\mathrm{\Omega }}_{11}|\hat{y}|+{\mathrm{\Omega }}_{12}|\hat{z}|)\\ +C{N}^{\frac{1}{2}+\gamma -m}({\mathrm{\Omega }}_{11}\parallel \hat{y}\parallel +{\mathrm{\Omega }}_{12}\parallel \hat{z}\parallel ),& \mathit{\text{otherwise}},\end{array}\hfill \end{array}$$

(3.6)

$$\begin{array}{c}\parallel {\hat{z}}_N-\hat{z}\parallel \le C{N}^{-m}(|f_1{|}_{H^{m,N}(\mathrm{\Lambda })}+(N^{-1}+N^{\frac{1}{2}})(|\hat{y}{|}_{H^{m,N}(\mathrm{\Lambda })}+|\hat{z}{|}_{H^{m,N}(\mathrm{\Lambda })}))\hfill \\ \phantom{\parallel {\hat{z}}_N-\hat{z}\parallel \le }+C{N}^{-1}(\parallel \hat{y}\parallel +\parallel \hat{z}\parallel )\hfill \\ \phantom{\parallel {\hat{z}}_N-\hat{z}\parallel \le }+\{\begin{array}{l}C{N}^{2-2m}logN(({\mathrm{\Omega }}_{11}+{\mathrm{\Omega }}_{21})|\hat{y}|+({\mathrm{\Omega }}_{12}+{\mathrm{\Omega }}_{22})|\hat{z}|)\\ +C{N}^{2-m}logN(({\mathrm{\Omega }}_{11}+{\mathrm{\Omega }}_{21})\parallel \hat{y}\parallel \\ +({\mathrm{\Omega }}_{12}+{\mathrm{\Omega }}_{22})\parallel \hat{z}\parallel ),& -1<\alpha ,\beta \le -\frac{1}{2},\\ C{N}^{\frac{5}{2}+\gamma -2m}(({\mathrm{\Omega }}_{11}+{\mathrm{\Omega }}_{21})|\hat{y}|+({\mathrm{\Omega }}_{12}+{\mathrm{\Omega }}_{22})|\hat{z}|)\\ +C{N}^{\frac{5}{2}+\gamma -m}(({\mathrm{\Omega }}_{11}+{\mathrm{\Omega }}_{21})\parallel \hat{y}\parallel \\ +({\mathrm{\Omega }}_{12}+{\mathrm{\Omega }}_{22})\parallel \hat{z}\parallel ),& \mathit{\text{otherwise}}\end{array}\hfill \end{array}$$

(3.7)

if N is sufficiently large, where ${\mathrm{\Omega }}_{ij}={max}_{0\le n\le N}|K_{ij}({\tau }_n,\eta ){|}_{H^{m,N}(\mathrm{\Lambda })}$ ($i,j=1,2$), $\gamma =max(\alpha ,\beta )$.

Proof Similar to the idea in [14], we let

$$\begin{array}{c}e(\tau )={\hat{y}}_N(\tau )-\hat{y}(\tau ),\epsilon (\tau )={\hat{z}}_N(\tau )-\hat{z}(\tau ),\hfill \\ S_1({\tau }_n)=\sum _{k=0}^N\sum _{l=k}^N{c}_{kl}{V}_{kl}({\tau }_n)-{\int }_{-1}^{{\tau }_n}{\hat{K}}_{11}({\tau }_n,\eta ){\hat{y}}_N(\eta )d\eta ,\hfill \\ S_2({\tau }_n)=\sum _{k=0}^N\sum _{l=k}^N{c}_{kl}^{\prime }{V}_{kl}({\tau }_n)-{\int }_{-1}^{{\tau }_n}{\hat{K}}_{12}({\tau }_n,\eta ){\hat{z}}_N(\eta )d\eta ,\hfill \\ S_3({\tau }_n)=\sum _{k=0}^N\sum _{l=k}^N{q}_{kl}{V}_{kl}({\tau }_n)-{\int }_{-1}^{{\tau }_n}{\hat{K}}_{21}({\tau }_n,\eta ){\hat{y}}_N(\eta )d\eta ,\hfill \\ S_4({\tau }_n)=\sum _{k=0}^N\sum _{l=k}^N{q}_{kl}^{\prime }{V}_{kl}({\tau }_n)-{\int }_{-1}^{{\tau }_n}{\hat{K}}_{22}({\tau }_n,\eta ){\hat{z}}_N(\eta )d\eta ,\hfill \\ F_1=I_N({\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )e(\eta )d\eta )-{\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )e(\eta )d\eta ,\hfill \\ F_2=I_N({\int }_{-1}^{\tau }{\hat{K}}_{12}(\tau ,\eta )\epsilon (\eta )d\eta )-{\int }_{-1}^{\tau }{\hat{K}}_{12}(\tau ,\eta )\epsilon (\eta )d\eta ,\hfill \\ F_3=I_N({\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )\hat{y}(\eta )d\eta )-{\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )\hat{y}(\eta )d\eta ,\hfill \\ F_4=I_N({\int }_{-1}^{\tau }{\hat{K}}_{12}(\tau ,\eta )\hat{z}(\eta )d\eta )-{\int }_{-1}^{\tau }{\hat{K}}_{12}(\tau ,\eta )\hat{z}(\eta )d\eta ,\hfill \\ F_5=I_N({\int }_{-1}^{\tau }{\hat{K}}_{21}(\tau ,\eta )e(\eta )d\eta )-{\int }_{-1}^{\tau }{\hat{K}}_{21}(\tau ,\eta )e(\eta )d\eta ,\hfill \\ F_6=I_N({\int }_{-1}^{\tau }{\hat{K}}_{22}(\tau ,\eta )\epsilon (\eta )d\eta )-{\int }_{-1}^{\tau }{\hat{K}}_{22}(\tau ,\eta )\epsilon (\eta )d\eta .\hfill \end{array}$$

From systems (2.2) and (2.7), we obtain

$$\begin{array}{c}e(\tau )={\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )e(\eta )d\eta +{\int }_{-1}^{\tau }{\hat{K}}_{12}(\tau ,\eta )\epsilon (\eta )d\eta +(I_N({\hat{f}}_1(\tau ))-{\hat{f}}_1(\tau ))\hfill \\ \phantom{e(\tau )=}+I_N(S_1(\tau ))+I_N(S_2(\tau ))+F_1+F_2+F_3+F_4,\hfill \end{array}$$

(3.8)

$$\begin{array}{c}-{\hat{K}}_{21}(\tau ,\tau )e(\tau )-{\hat{K}}_{22}(\tau ,\tau )\epsilon (\tau )={\int }_{-1}^{\tau }\frac{\partial {\hat{K}}_{21}(\tau ,\eta )}{\partial \tau }e(\eta )d\eta +{\int }_{-1}^{\tau }\frac{\partial {\hat{K}}_{22}(\tau ,\eta )}{\partial \tau }\epsilon (\eta )d\eta \hfill \\ \phantom{-{\hat{K}}_{21}(\tau ,\tau )e(\tau )-{\hat{K}}_{22}(\tau ,\tau )\epsilon (\tau )=}+I_N^{\prime }(S_3(\tau ))+I_N^{\prime }(S_4(\tau ))+F_5^{\prime }+F_6^{\prime }.\hfill \end{array}$$

(3.9)

Equations (3.8) and (3.9) can be written in the compact matrix representation:

$$A(\tau )E(\tau )={\int }_{-1}^{\tau }K(\tau ,\eta )E(\eta )d\eta +B$$

(3.10)

with

$$\begin{array}{c}A(\tau )=\left[\begin{array}{cc}1& 0\\ -{\hat{K}}_{21}(\tau ,\tau )& -{\hat{K}}_{22}(\tau ,\tau )\end{array}\right],\hfill \\ K(\tau ,\eta )=\left[\begin{array}{cc}{\hat{K}}_{11}(\tau ,\eta )& {\hat{K}}_{12}(\tau ,\eta )\\ \frac{\partial {\hat{K}}_{21}(\tau ,\eta )}{\partial \tau }& \frac{\partial {\hat{K}}_{21}(\tau ,\eta )}{\partial \tau }\end{array}\right],E(\tau )=\left(\begin{array}{c}e(\tau )\\ \epsilon (\tau )\end{array}\right)\hfill \end{array}$$

and

$$B=\left(\begin{array}{c}(I_N({\hat{f}}_1(\tau ))-{\hat{f}}_1(\tau ))+I_N(S_1(\tau ))+I_N(S_2(\tau ))+F_1+F_2+F_3+F_4\\ I_N^{\prime }(S_3(\tau ))+I_N^{\prime }(S_4(\tau ))+F_5^{\prime }+F_6^{\prime }\end{array}\right).$$

Since $|k_{22}(\tau ,\tau )|\ge k_0>0$, the inverse of the matrix $A(\tau )$ exists and

$$A^{-1}(\tau )=\left[\begin{array}{cc}1& 0\\ \frac{-{\hat{K}}_{21}(\tau ,\tau )}{{\hat{K}}_{22}(\tau ,\tau )}& -\frac{1}{{\hat{K}}_{22}(\tau ,\tau )}\end{array}\right].$$

Using the Gronwall inequality (see, e.g., [[20], Lemma 3.4]) on (3.10), we have

$$\parallel E\parallel \le C\parallel F\parallel .$$

(3.11)

Here $F=A^{-1}B$.

It follows from (3.4) that

$$\begin{array}{c}\parallel (I_N({\hat{f}}_1(\tau ))-{\hat{f}}_1(\tau ))\parallel \le C{N}^{-m}|{\hat{f}}_1{|}_{H^{m,N}(\mathrm{\Lambda })},\hfill \\ \parallel e(\tau )\parallel \le C{N}^{-m}|\hat{y}{|}_{H^{m,N}(\mathrm{\Lambda })},\hfill \\ \parallel \epsilon (\tau )\parallel \le C{N}^{-m}|\hat{z}{|}_{H^{m,N}(\mathrm{\Lambda })}.\hfill \end{array}$$

(3.12)

Using (3.4), (3.3) for $m=1$ and the Hardy inequality [[21], Lemma 3.8], we obtain

$$\begin{array}{rcl}\parallel F_1\parallel & \le & C{N}^{-1}\parallel {({\int }_{-1}^{\tau }{\hat{K}}_{11}(\tau ,\eta )e(\eta )d\eta )}_{\tau }^{\prime }\parallel \\ \le & C{N}^{-1}\parallel -{\hat{K}}_{11}(\tau ,\tau )e(\tau )+{\int }_{-1}^{\tau }\frac{\partial {\hat{K}}_{11}(\tau ,\eta )}{\partial \tau }e(\eta )d\eta \parallel \\ \le & C{N}^{-1}\parallel {\hat{K}}_{11}(\tau ,\tau )+C\parallel \parallel e(\tau )\parallel \\ \le & C{N}^{-1-m}|\hat{y}{|}_{H^{m,N}(\mathrm{\Lambda })},\end{array}$$

(3.13)

and consequently

$$\parallel F_2\parallel \le C{N}^{-1-m}|\hat{z}{|}_{H^{m,N}(\mathrm{\Lambda })},$$

(3.14)

$$\parallel F_3\parallel \le C{N}^{-1}\parallel \hat{y}\parallel ,$$

(3.15)

$$\parallel F_4\parallel \le C{N}^{-1}\parallel \hat{z}\parallel .$$

(3.16)

Also,

$$I_N(S_1(\tau ))=\sum _{n=0}^N{S}_1({\tau }_n)L_n(\tau ),$$

(3.17)

where $L_n(\tau )$ is the Lagrange interpolation polynomial based on the Gauss quadrature nodes (see [19]). Therefore, we have

$$\parallel I_N(S_1(\tau ))\parallel \le \underset{0\le n\le N}{max}|S_1({\tau }_n)|\underset{-1\le \tau \le 1}{max}\sum _{n=0}^N{L}_n(\tau ).$$

Moreover, using the Cauchy-Schwarz inequality [15], we have

$$\begin{array}{rl}|S_1({\tau }_n)|& \le |{\int }_{-1}^{{\tau }_n}(I_N({\hat{K}}_{11}({\tau }_n,\eta ))-{\hat{K}}_{11}({\tau }_n,\eta )){\hat{y}}_N(\eta )d\eta |\\ \le \parallel I_N({\hat{K}}_{11}({\tau }_n,\eta ))-{\hat{K}}_{11}({\tau }_n,\eta )\parallel \parallel {\hat{y}}_N\parallel .\end{array}$$

By (3.4), we have

$$|S_1({\tau }_n)|\le C{N}^{-m}|{\hat{K}}_{11}({\tau }_n,\eta ){|}_{H^{m,N}(\mathrm{\Lambda })}(\parallel e\parallel +\parallel \hat{y}\parallel ).$$

(3.18)

Now, we will make use of the result of Chen and Tang [[21], Lemma 3.4], which gives the Lebesgue constant for the Lagrange interpolating polynomials with the nodes of the Jacobi polynomials. Actually, the following relation holds:

$$\underset{-1\le \tau \le 1}{max}\sum _{n=0}^N{L}_n(\tau )=\{\begin{array}{ll}\mathrm{O}(logN),& -1<\alpha ,\beta \le -\frac{1}{2},\\ \mathrm{O}(N^{\gamma +\frac{1}{2}}),& \gamma =max(\alpha ,\beta ),\text{otherwise}.\end{array}$$

(3.19)

So we obtain

$$\parallel I_N(S_1(\tau ))\parallel \le \{\begin{array}{ll}C{N}^{-m}logN{\mathrm{\Omega }}_{11}(\parallel e\parallel +\parallel \hat{y}\parallel ),& -1<\alpha ,\beta \le -\frac{1}{2},\\ C{N}^{\frac{1}{2}+\gamma -m}{\mathrm{\Omega }}_{11}(\parallel e\parallel +\parallel \hat{y}\parallel ),& \text{otherwise}.\end{array}$$

(3.20)

Similarly,

$$\parallel I_N(S_2(\tau ))\parallel \le \{\begin{array}{ll}C{N}^{-m}logN{\mathrm{\Omega }}_{12}(\parallel \epsilon \parallel +\parallel \hat{z}\parallel ),& -1<\alpha ,\beta \le -\frac{1}{2},\\ C{N}^{\frac{1}{2}+\gamma -m}{\mathrm{\Omega }}_{12}(\parallel \epsilon \parallel +\parallel \hat{z}\parallel ),& \text{otherwise}.\end{array}$$

(3.21)

It then follows from (3.1), (3.20), and (3.21) that

$$\begin{array}{rcl}\parallel I_N^{\prime }(S_3(\tau ))\parallel & \le & C{N}^2\parallel I_N(S_3(\tau ))\parallel \\ \le & \{\begin{array}{ll}C{N}^{-m}logN{\mathrm{\Omega }}_{21}(\parallel e\parallel +\parallel \hat{y}\parallel ),& -1<\alpha ,\beta \le -\frac{1}{2},\\ C{N}^{\frac{1}{2}+\gamma -m}{\mathrm{\Omega }}_{21}(\parallel e\parallel +\parallel \hat{y}\parallel ),& \text{otherwise}.\end{array}\end{array}$$

(3.22)

Similarly,

$$\begin{array}{rcl}\parallel I_N^{\prime }(S_4(\tau ))\parallel & \le & C{N}^2\parallel I_N(S_4(\tau ))\parallel \\ \le & \{\begin{array}{ll}C{N}^{-m}logN{\mathrm{\Omega }}_{22}(\parallel \epsilon \parallel +\parallel \hat{z}\parallel ),& -1<\alpha ,\beta \le -\frac{1}{2},\\ C{N}^{\frac{1}{2}+\gamma -m}{\mathrm{\Omega }}_{22}(\parallel \epsilon \parallel +\parallel \hat{z}\parallel ),& \text{otherwise}.\end{array}\end{array}$$

(3.23)

Using (3.2) and letting $l=1$ in (3.5), we have

$$\parallel F_5^{\prime }\parallel \le {\parallel F_5\parallel }_{H^l(\mathrm{\Lambda })}\le C{N}^{\frac{3}{2}-m}|{\int }_{-1}^{\tau }{\hat{K}}_{21}(\tau ,\eta )e(\eta )d\eta {|}_{H^{m,N}(\mathrm{\Lambda })}.$$

Applying (3.3) for $m=1$, we have

$$\parallel F_5^{\prime }\parallel \le C{N}^{\frac{1}{2}}\parallel {\hat{K}}_{21}(\tau ,\tau )e(\tau )+{\int }_{-1}^{\tau }\frac{\partial {\hat{K}}_{21}(\tau ,\eta )}{\partial \tau }e(\eta )d\eta \parallel \le C{N}^{\frac{1}{2}-m}|\hat{y}{|}_{H^{m,N}(\mathrm{\Lambda })}.$$

(3.24)

Similarly,

$$\parallel F_6^{\prime }\parallel \le C{N}^{\frac{1}{2}-m}|\hat{z}{|}_{H^{m,N}(\mathrm{\Lambda })}.$$

(3.25)

Finally, combining the above estimates and (3.11), the desired error estimates (3.6) and (3.7) are obtained. □

4 Numerical experiments

In this section, we consider some numerical examples in order to illustrate the validity of the proposed Jacobi collocation method. These problems are solved using the Jacobi collocation method for $\alpha =1/2$, $\beta =1/3$. All the computations were performed using software Matlab®. To examine the accuracy of the results, $L_{{\omega }^{\alpha ,\beta }}^2(-1,1)$ errors are employed to verify the efficiency of the method. To find the numerical convergence order in the numerical examples, we assume that $E_N=C{(\frac{1}{N})}^p$, where $E_N$ denotes the $L_{{\omega }^{\alpha ,\beta }}^2(-1,1)$ errors between the numerical and exact solution of the system and C denotes some positive constant. Thus, the convergence order p can be computed by $p=\frac{{log}_2(E_{N/2})}{{log}_2(E_N)}$.

Example 4.1 Consider the following linear system of IAEs of index 1:

$$A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)ds,t\in [0,1],$$

where

$$A(t)=\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right),X(t)=\left(\begin{array}{c}y(t)\\ z(t)\end{array}\right),K(t,s)=\left(\begin{array}{cc}{t}^3+s+1& cos(3s)+1\\ t+s+2& sin(3s)+2\end{array}\right),$$

and $g(t)={(f_1(t),f_2(t))}^T$ are chosen so that the exact solutions of this system are

$$y(t)=cost,z(t)=sin3t.$$

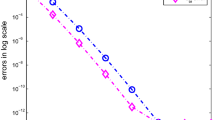
Let $({\hat{y}}_N,{\hat{z}}_N)$ and $(\hat{y},\hat{z})$ be the approximate and the exact solution of the system, respectively. The $L_{{\omega }^{\alpha ,\beta }}^2(-1,1)$-norm of the errors and orders of convergence are given in Tables 1 and 2.

Table 1 ${\mathit{L}}_{{\mathit{\omega }}^{\mathit{\alpha }\mathbf{,}\mathit{\beta }}}^{\mathbf{2}}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{1}\mathbf{)}$ errors for Example 4.1

Table 2 Convergence orders for Example 4.1

Example 4.2 Consider the following linear system of IAEs of index 1:

$$A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)ds,t\in [0,1],$$

where

$$A(t)=\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right),X(t)=\left(\begin{array}{c}y(t)\\ z(t)\end{array}\right),K(t,s)=\left(\begin{array}{cc}{t}^2+s^2+2& s+t+1\\ e^{2t+s}& s+t^2+2\end{array}\right),$$

and $g(t)={(f_1(t),f_2(t))}^T$ are chosen so that the exact solutions of this system are

$$y(t)=e^{2t},z(t)=\frac{1}{1+t^2}.$$

The computational results have been reported in Tables 3 and 4.

Table 3 ${\mathit{L}}_{{\mathit{\omega }}^{\mathit{\alpha }\mathbf{,}\mathit{\beta }}}^{\mathbf{2}}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{1}\mathbf{)}$ errors for Example 4.2

Table 4 Convergence orders for Example 4.2

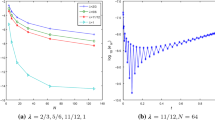
It can be seen from Tables 1 and 3 that the errors decay exponentially and the rates of convergence for $\hat{y}$ are larger than those for $\hat{z}$. Tables 2 and 4 also shows that the orders of convergence for $\hat{y}$ are higher than those for $\hat{z}$. In fact, it is noted that the differences of the convergence orders for $\hat{y}$ and $\hat{z}$ are about 2 from Tables 2 and 4. Although the exact solutions of Examples 4.1 and 4.2 are infinitely differentiable functions, it can be implied, from Theorem 3.1, that a conservative estimate of the numerical convergence order for system (1.1) is only 1. However, from numerical experiments, the numerical convergence order is much higher than 1.

Example 4.3 Consider the following linear system of IAEs:

$$A(t)X(t)=g(t)+{\int }_0^{t}K(t,s)X(s)ds,t\in [0,1],$$

where

$$A(t)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right),X(t)=\left(\begin{array}{c}{x}_1(t)\\ x_2(t)\\ x_3(t)\end{array}\right),K(t,s)=\left(\begin{array}{ccc}\frac{3-2s}{2-s}& \frac{3-s}{2-s}& 2(2-s)\\ \frac{-1}{s-2}& -1& 1\\ s+2& s^2-4& 2-s\end{array}\right),$$

and $g(t)={(f_1(t),f_2(t),f_3(t))}^T$ are chosen so that the exact solutions of this system are

$$x_1(t)=x_2(t)=e^t,x_3(t)=\frac{e^t}{t-2}.$$

Let u, v, w be the approximations of the exact solutions $x_1$, $x_2$, $x_3$, respectively. The errors and orders of convergence for the proposed method with several values of N are reported in Tables 5 and 6. The results show that the methods are convergent with a good accuracy.

Table 5 ${\mathit{L}}_{{\mathit{\omega }}^{\mathit{\alpha }\mathbf{,}\mathit{\beta }}}^{\mathbf{2}}\mathbf{(}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{1}\mathbf{)}$ errors for Example 4.3

Table 6 Convergence orders for Example 4.3

5 Conclusions

This paper studies the Jacobi collocation method for the semi-explicit IAEs system of index 1. The scheme consists of finding an explicit expression for the integral terms of the equations associated with the Jacobi collocation method. A posteriori error estimation of the method in the weighted $L^2$-norm was obtained. With the availability of this methodology, it will now be possible to investigate the approximate solution of other classes of IAEs systems. Although our convergence theory does not cover the nonlinear case, it contains some complications and restrictions for establishing a convergent result similar to Theorem 3.1 which will be the subject of our future work.