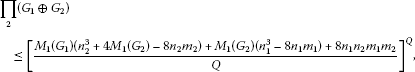Abstract
Recently, Todeschini et al. (Novel Molecular Structure Descriptors - Theory and Applications I, pp. 73-100, 2010), Todeschini and Consonni (MATCH Commun. Math. Comput. Chem. 64:359-372, 2010) have proposed the multiplicative variants of ordinary Zagreb indices, which are defined as follows:
These two graph invariants are called multiplicative Zagreb indices by Gutman (Bull. Soc. Math. Banja Luka 18:17-23, 2011). In this paper the upper bounds on the multiplicative Zagreb indices of the join, Cartesian product, corona product, composition and disjunction of graphs are derived and the indices are evaluated for some well-known graphs.
MSC:05C05, 05C90, 05C07.
Similar content being viewed by others
1 Introduction
Throughout this paper, we consider simple graphs which are finite, indirected graphs without loops and multiple edges. Suppose G is a graph with a vertex set and an edge set . For a graph G, the degree of a vertex v is the number of edges incident to v and is denoted by . A topological index of a graph G is a number with the property that for every graph H isomorphic to G, . Recently, Todeschini et al. [1, 2] have proposed the multiplicative variants of ordinary Zagreb indices, which are defined as follows:
Mathematical properties and applications of multiplicative Zagreb indices are reported in [1–6]. Mathematical properties and applications of multiplicative sum Zagreb indices are reported in [7]. For other undefined notations and terminology from graph theory, the readers are referred to [8].
In [9, 10], Khalifeh et al. computed some exact formulae for the hyper-Wiener index and Zagreb indices of the join, Cartesian product, composition, disjunction and symmetric difference of graphs. Some more properties and applications of graph products can be seen in the classical book [11].
In this paper, we give some upper bounds for the multiplicative Zagreb index of various graph operations such as join, corona product, Cartesian product, composition, disjunction, etc. Moreover, computations are done for some well-known graphs.
2 Multiplicative Zagreb index of graph operations
We begin this section with two standard inequalities as follows.
Lemma 1 (AM-GM inequality)
Let be nonnegative numbers. Then
holds with equality if and only if all the ’s are equal.
Lemma 2 (Weighted AM-GM inequality)
Let be nonnegative numbers and also let be nonnegative weights. Set . If , then the inequality
holds with equality if and only if all the with are equal.
Let and be two graphs with and vertices and and edges, respectively. The join of graphs and with disjoint vertex sets and and edge sets and is the graph union together with all the edges joining and . Thus, for example, , the complete bipartite graph. We have and .
Theorem 1 Let and be two graphs. Then
and
where and are the numbers of vertices of and , and , are the numbers of edges of and , respectively. Moreover, the equality holds in (3) if and only if both and are regular graphs, that is, is a regular graph and the equality holds in (4) if and only if both and are regular graphs, that is, is a regular graph.
Proof
Now,
and by (1) this above equality is actually less than or equal to

Moreover, the above equality holds if and only if
and
(by Lemma 1), that is, for and ,
and
That is, for and , we get and . Hence the equality holds in (3) if and only if both and are regular graphs, that is, is a regular graph.
Now, since
we then obtain

and by (1)

However, from the last inequality, we get

Furthermore, for both connected graphs and , the equality holds in (5) iff
for any ; and
for any as well as

for any , ; and

for any , by Lemma 1. Thus one can easily see that the equality holds in (5) if and only if for and ,
Hence the equality holds in (4) if and only if both and are regular graphs, that is, is a regular graph. □
Example 1 Consider two cycle graphs and . We thus have
The Cartesian product of graphs and has the vertex set and is an edge of if

Theorem 2 Let and be two connected graphs. Then
-
(i)
(6)
The equality holds in (6) if and only if is a regular graph.
-
(ii)
(7)
Moreover, the equality holds in (7) if and only if is a regular graph.
Proof
By the definition of the first multiplicative Zagreb index, we have
On the other hand, by (1)
But as and , the last statement in (8) is less than or equal to
which equals to
Moreover, the equality holds in (8) if and only if for any by Lemma 1. Since both and are connected graphs, one can easily see that the equality holds in (8) if and only if , and , . Hence the equality holds in (6) if and only if both and are regular graphs, that is, is a regular graph. This completes the first part of the proof.
By the definition of the second multiplicative Zagreb index, we have
This actually can be written as
or, equivalently,
After that, by (2) we get
Moreover, since

By (1) the final statement in (9) becomes

Hence the second part of the proof is over.
The equality holds in (9) and (10) if and only if for any and for any by Lemmas 1 and 2. Hence the equality holds in (7) if and only if both and are regular graphs, that is, is a regular graph. This completes the proof. □
Example 2 Consider a cycle graph and a complete graph . We thus have
The corona product of two graphs and is defined to be the graph Γ obtained by taking one copy of (which has vertices) and copies of , and then joining the i th vertex of to every vertex in the i th copy of , .
Let and be two graphs such that , and , . Then it follows from the definition of the corona product that has vertices and edges, where and . It is clear that if is connected, then is connected, and in general is not isomorphic to .
Theorem 3 The first and second multiplicative Zagreb indices of the corona product are computed as follows:
-
(i)
(11)
-
(ii)
(12)
where and are the first and second Zagreb indices of , where , respectively. Moreover, both equalities in (11) and (12) hold if and only if is a regular graph.
Proof
By the definition of the first multiplicative Zagreb index, we have
The equality holds in (13) if and only if , and , , that is, both and are regular graphs, that is, is a regular graph.
By the definition of the second multiplicative Zagreb index, we have
The above equality holds if and only if for any and for any , that is, both and are regular graphs, which implies that is a regular graph. This completes the proof. □
Example 3 and .
The composition (also called lexicographic product [12]) of graphs and with disjoint vertex sets and and edge sets and is the graph with a vertex set and is adjacent to whenever

Theorem 4 The first and second multiplicative Zagreb indices of the composition of graphs and are bounded above as follows:
-
(i)
(14)
-
(ii)
(15)
where and are the first and second Zagreb indices of , where . Moreover, the equalities in (14) and (15) hold if and only if is a regular graph.
Proof
By the definition of the first multiplicative Zagreb index, we have

The equality holds in (16) if and only if , and , (by Lemma 1), that is, both and are regular graphs, that is, is a regular graph.
By the definition of the second multiplicative Zagreb index, we have


which gives the required result in (15).
The equality holds in (17) and (18) if and only if , and , (by Lemma 1), that is, both and are regular graphs, that is, is a regular graph. □
Example 4 and .
The disjunction of graphs and is the graph with a vertex set and is adjacent to whenever or .
Theorem 5 The first and second multiplicative Zagreb indices of the disjunction are computed as follows:
-
(i)
(19)
-
(ii)
 (20)
(20)
where and is the first Zagreb index of , . Moreover, the equalities in (19) and (20) hold if and only if is a regular graph.
Proof We have . By the definition of the first multiplicative Zagreb index, we have

The equality holds in (21) if and only if , and , (by Lemma 1), that is, both and are regular graphs, that is, is a regular graph.
By the definition of the second multiplicative Zagreb index, we have
where
Using the weighted arithmetic-geometric mean inequality in (2), is less than or equal to

where
Hence the first part of the proof is over.
The equality holds in (22) if and only if , where and , where (by Lemma 1), that is, both and are regular graphs, and so the graph is regular. □
Example 5 and .
The symmetric difference of two graphs and is the graph with a vertex set in which is adjacent to whenever is adjacent to in or is adjacent to in , but not both. The degree of a vertex of is given by
while the number of edges in is .
Theorem 6 The first and second multiplicative Zagreb indices of the symmetric difference of two graphs and are bounded above as follows:
-
(i)
(23)
-
(ii)
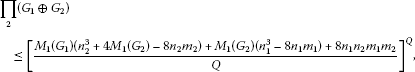 (24)
(24)
where and is the first Zagreb index of , for . Moreover, the equalities in (23) and (24) hold if and only if is a regular graph.
Proof
We have
By the definition of the first multiplicative Zagreb index, we have

The equality holds in (25) if and only if , and , (by Lemma 1), that is, both and are regular graphs, which implies that is a regular graph.
By the definition of the second multiplicative Zagreb index, we have
where .
Using the weighted arithmetic-geometric mean inequality in (2), we get

where . First part of the proof is over.
The equality holds in (26) if and only if , and , (by Lemma 1), that is, both and are regular graphs, which implies that is a regular graph. □
Example 6 and .
References
Todeschini R, Ballabio D, Consonni V: Novel molecular descriptors based on functions of new vertex degrees. In Novel Molecular Structure Descriptors - Theory and Applications I. Edited by: Gutman I, Furtula B. Univ. Kragujevac, Kragujevac; 2010:73–100.
Todeschini R, Consonni V: New local vertex invariants and molecular descriptors based on functions of the vertex degrees. MATCH Commun. Math. Comput. Chem. 2010, 64: 359–372.
Eliasi M, Iranmanesh A, Gutman I: Multiplicative versions of first Zagreb index. MATCH Commun. Math. Comput. Chem. 2012, 68: 217–230.
Gutman I: Multiplicative Zagreb indices of trees. Bull. Soc. Math. Banja Luka 2011, 18: 17–23.
Liu J, Zhang Q: Sharp upper bounds on multiplicative Zagreb indices. MATCH Commun. Math. Comput. Chem. 2012, 68: 231–240.
Xu K, Hua H: A unified approach to extremal multiplicative Zagreb indices for trees, unicyclic and bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2012, 68: 241–256.
Xu K, Das KC: Trees, unicyclic and bicyclic graphs extremal with respect to multiplicative sum Zagreb index. MATCH Commun. Math. Comput. Chem. 2012, 68(1):257–272.
Bondy JA, Murty USR: Graph Theory with Applications. Macmillan Co., New York; 1976.
Khalifeh MH, Azari HY, Ashrafi AR: The hyper-Wiener index of graph operations. Comput. Math. Appl. 2008, 56: 1402–1407. 10.1016/j.camwa.2008.03.003
Khalifeh MH, Azari HY, Ashrafi AR: The first and second Zagreb indices on of some graph operations. Discrete Appl. Math. 2009, 157: 804–811. 10.1016/j.dam.2008.06.015
Imrich W, Klavžar S: Product Graphs: Structure and Recognition. Wiley, New York; 2000.
Harary F: Graph Theory. Addison-Wesley, Reading; 1994:22.
Acknowledgements
Dedicated to Professor Hari M Srivastava.
All authors except the first one are partially supported by Research Project Offices of Uludağ (2012-15 and 2012-19) and Selçuk Universities. K.C. Das thanks for support the Sungkyunkwan University BK21 Project, BK21 Math Modeling HRD Div. Sungkyunkwan University, Suwon, Republic of Korea.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors completed the paper together. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Das, K.C., Yurttas, A., Togan, M. et al. The multiplicative Zagreb indices of graph operations. J Inequal Appl 2013, 90 (2013). https://doi.org/10.1186/1029-242X-2013-90
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-90