On containment measure and the mixed isoperimetric inequality

Abstract

We first investigate whether for given convex domains $K_0$, $K_1$ in the Euclidean plane, for any rotation α, there is a translation x so that $x+\alpha K_1\subset K_0$ or $x+\alpha K_1\supset K_0$. Then, we estimate the mixed isoperimetric deficit ${\mathrm{\Delta }}_2(K_0,K_1)$ of domains $K_0$ and $K_1$ via the known kinematic formulas of Poincaré and Blaschke in integral geometry. We obtain the sufficient condition for domain $K_0$ to contain, or to be contained in, convex domain $x+\alpha K_1$. Finally, we obtain the mixed isoperimetric inequality and some Bonnesen-style mixed inequalities. Those Bonnesen-style mixed inequalities obtained are the known Bonnesen-style inequalities if one of the domains is a disc. As a direct consequence, we obtain the strengthened Bonnesen isoperimetric inequality.

MSC:52A10, 52A22.

1 Introductions and preliminaries

A set of points K in the Euclidean space $R^n$ is convex if for all $x,y\in K$ and $0\le \lambda \le 1$, $\lambda x+(1-\lambda )y\in K$. The convex hull $K^{\ast }$ of K is the intersection of all convex sets that contain K. The Minkowski sum of convex sets K and L is defined by

$$K+L=\{x+y:x\in K,y\in L\},$$

and the scalar product of convex set K for $\lambda \ge 0$ is defined by

$$\lambda K=\{\lambda x:x\in K\}.$$

A homothety of a convex set K is of the form $x+\lambda K$ for $x\in R^n$, $\lambda >0$. A convex body is a compact convex set with nonempty interior. A domain is a set with nonempty interior.

One may be interested in the following strong containment problem: Whether for given convex domains $K_0$ and $K_1$, there exists a translation x so that $x+\alpha K_0\subset K_1$ or $x+\alpha K_1\subset K_0$ for any rotation α. It should be noted that this containment problem is much stronger than Hadwiger’s one. Therefore, the strong containment problem could lead to general and fundamental geometric inequalities (cf. [1–9]).

The well-known classical isoperimetric problem says that the disc encloses the maximum area among all domains of fixed perimeters in the Euclidean plane $R^2$.

Proposition 1 Let Γ be a simple closed curve of length P in the Euclidean plane $R^2$, then the area A of the domain K enclosed by Γ satisfies

$$P^2-4\pi A\ge 0.$$

(1)

The equality sign holds if and only if Γ is a circle.

Its analytic proofs root back to centuries ago. One can find some simplified and beautiful proofs that lead to generalizations of the discrete case, higher dimensions, the surface of constant curvature and applications to other branches of mathematics (cf. [1, 3–5, 10–53]).

The isoperimetric deficit

$${\mathrm{\Delta }}_2(K)=P^2-4\pi A$$

(2)

measures the difference between domain K of area A and perimeter P, and a disc of radius $P/2\pi$.

During the 1920s, Bonnesen proved a series of inequalities of the form

$${\mathrm{\Delta }}_2(K)=P^2-4\pi A\ge B_K,$$

(3)

where the quantity $B_K$ is an invariant of geometric significance having the following basic properties:

• 1. $B_K$ is nonnegative;

• 2. $B_K$ is vanish only when K is a disc.

Many $B_K$s are found during the past. The main interest is still focusing on those unknown invariants of geometric significance. See references [3–5, 12, 17, 23, 31, 32, 36] for more details. The following Bonnesen’s isoperimetric inequality is well known.

Proposition 2 Let K be a domain of area A, bounded by a simple closed curve of perimeter P in the Euclidean plane $R^2$. Let r and R be, respectively, the maximum inscribed radius and minimum circumscribed radius of K. Then we have the following Bonnesen’s isoperimetric inequality:

$$P^2-4\pi A\ge {\pi }^2{(R-r)}^2,$$

(4)

where the equality holds if and only if K is a disc.

Since for any domain K in $R^2$, its convex hull $K^{\ast }$ increases the area $A^{\ast }$ and decreases the perimeter $P^{\ast }$, that is, $A^{\ast }\ge A$ and $P^{\ast }\le P$, then we have $P^2-4\pi A\ge {P^{\ast }}^2-4\pi A^{\ast }$, that is, ${\mathrm{\Delta }}_2(K)\ge {\mathrm{\Delta }}_2(K^{\ast })$. Therefore, the isoperimetric inequality and the Bonnesen-style inequality are valid for all domains in $R^2$ if these inequalities are valid for convex domains.

In this paper, we first investigate the stronger containment problem: Whether for given convex bodies $K_0$, $K_1$ in the Euclidean plane $R^2$, there is a translation x so that $x+\alpha K_0\subset K_1$ or $x+\alpha K_1\subset K_0$ for any rotation α. Then we investigate the mixed isoperimetric deficit ${\mathrm{\Delta }}_2(K_0,K_1)$ of domains $K_0$ and $K_1$.

Definition 1 Let $K_0$ and $K_1$ be two domains of areas $A_0$ and $A_1$, and of perimeters $P_0$ and $P_1$, respectively. Then the mixed isoperimetric deficit of $K_0$ and $K_1$ is defined as

$${\mathrm{\Delta }}_2(K_0,K_1)=P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1.$$

(5)

Since the convex hull $K^{\ast }$ of a set K in the Euclidean plane $R^2$ decreases the circum perimeter and increases the area, we have

$${\mathrm{\Delta }}_2(K_0,K_1)=P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {P_0^{\ast }}^2{P_1^{\ast }}^2-16{\pi }^2{A}_0^{\ast }{A}_1^{\ast }={\mathrm{\Delta }}_2(K_0^{\ast },K_1^{\ast }).$$

Therefore, we can only consider the convex domains when we estimate the mixed isoperimetric deficit low bound.

Via the kinematic formulas of Poincaré and Blaschke in integral geometry, we obtain sufficient conditions for convex domain $K_1$ to contain, or to be contained in, another convex domain $K_0$ for a translation x and any rotation α (Theorem 1 and Theorem 2). We obtain the mixed isoperimetric inequality and some Bonnesen-style mixed inequalities (Theorem 3, Theorem 4, Corollary 2, Corollary 3, Corollary 4, Theorem 5 and Theorem 6). One immediate consequence of our results is the strengthening Bonnesen isoperimetric inequality (Corollary 3). These new Bonnesen-style mixed inequalities obtained are fundamental and generalize some known Bonnesen-style inequalities (Corollary 5).

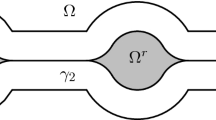
2 The containment measure

Let $K_k$ ($k=0,1$) be two domains of areas $A_k$ with simple boundaries of perimeters $P_k$ in the Euclidean plane $R^2$. Let dg denote the kinematic density of the group $G_2$ of rigid motions, that is, translations and rotations, in $R^2$. Let $K_1$ be convex, and let $t{K}_1$ ($t\in (0,+\mathrm{\infty })$) be a homothetic copy of $K_1$, then we have the known kinematic formula of Poincaré (cf. [3, 36])

$${\int }_{\{g\in G_2:\partial K_0\cap t\partial (g{K}_1)\ne \mathrm{\varnothing }\}}n\{\partial K_0\cap t\partial (g{K}_1)\}dg=4t{P}_0{P}_1,$$

(6)

where $n\{\partial K_0\cap t\partial (g{K}_1)\}$ denotes the number of points of intersection $\partial K_0\cap t\partial (g{K}_1)$.

Let $m_n$ be the kinematic measure of the set of positions g, for which $t\partial (g{K}_1)$ has exactly n intersection points with $\partial K_0$, i.e., $m_n=m\{g\in G_2:n\{\partial (K_0)\cap t\partial (g{K}_1)\}=n\}$. Notice that the measure $m_n=0$ for the odd n, then the formula of Poincaré can be rewritten as

$$\sum _{n=1}^{\mathrm{\infty }}(2n)m_{2n}=4t{P}_0{P}_1,$$

that is,

$$\sum _{n=1}^{\mathrm{\infty }}n{m}_{2n}=2t{P}_0{P}_1.$$

(7)

We consider the homothetic copy $t{K}_1$ ($t\in (0,+\mathrm{\infty })$) of $K_1$.

Let $\chi (K_0\cap t(g{K}_1))$ be the Euler-Poincaré characteristics of the intersection $K_0\cap t(g{K}_1)$. From the Blaschke’s kinematic formula (cf. [3, 36]):

$${\int }_{\{g\in G_2:K_0\cap t(g{K}_1)\ne \mathrm{\varnothing }\}}\chi (K_0\cap t(g{K}_1))dg=2\pi (t^2{A}_1+A_0)+t{P}_0{P}_1,$$

(8)

we have

$$\sum _{n=1}^{\mathrm{\infty }}{m}_{2n}=2\pi (t^2{A}_1+A_0)+t{P}_0{P}_1.$$

(9)

The formula of Poincaré (7) and the formula of Blaschke (9) give

$$\sum _{n=2}^{\mathrm{\infty }}{m}_{2n}(n-1)=t{P}_0{P}_1-2\pi (t^2{A}_1+A_0).$$

Since all $m_k$ are non-negative, we have

$$t{P}_0{P}_1-2\pi (t^2{A}_1+A_0)\ge 0;t\in (0,+\mathrm{\infty }).$$

(10)

On the other hand, since domains $K_k$ ($k=0,1$) are assumed to be simply connected and bounded by simple curves, we have $\chi (K_0\cap t(g{K}_1))=n(g)=$ the number of connected components of the intersection $K_0\cap g(t{K}_1)$. The fundamental kinematic formula of Blaschke (8) can be rewritten as

$${\int }_{\{g\in G_2:K_0\cap t(g{K}_1)\ne \mathrm{\varnothing }\}}n(g)dg=2\pi (t^2{A}_1+A_0)+t{P}_0{P}_1.$$

(11)

If μ denotes set of all positions of $K_1$, in which either $t(g{K}_1)\subset K_0$ or $t(g{K}_1)\supset K_0$, then the above formula of Blaschke can be rewritten as

$${\int }_{\mu }dg+{\int }_{\{g\in G_2:\partial K_0\cap t\partial (g{K}_1)\ne \mathrm{\varnothing }\}}n(g)dg=2\pi (t^2{A}_1+A_0)+t{P}_0{P}_1.$$

(12)

When $\partial K_0\cap t\partial (g{K}_1)\ne \mathrm{\varnothing }$, each component of $K_0\cap t(g{K}_1)$ is bounded by at least an arc of $\partial K_0$ and an arc of $t\partial (g{K}_1)$. Therefore, $n(g)\le n\{\partial K_0\cap t\partial (g{K}_1)\}/2$. Then by formulas of Poincaré and Blaschke, we obtain

$${\int }_{\mu }dg\ge 2\pi (t^2{A}_1+A_0)-t{P}_0{P}_1.$$

(13)

Therefore, this inequality immediately gives the following answer for the strong containment problem (cf. [1–9, 17, 36, 50, 54–60]).

Theorem 1 Let $K_k$ ($k=0,1$) be two domains of areas $A_k$ with simple boundaries of perimeters $P_k$ in $R^2$. Let $K_1$ be convex. A sufficient condition for $t{K}_1$ to contain, or to be contained in, another domain $K_0$ for a translation and any rotation, is

$$2\pi A_1{t}^2-P_0{P}_{1}t+2\pi A_0>0.$$

(14)

Moreover, if $t^2{A}_1\ge A_0$, then $t{K}_1$ contains $K_0$.

As a direct consequence of Theorem 1, we have the following analog of Ren’s theorem (cf. [36, 50, 58–60]).

Theorem 2 Let $K_k$ ($k=0,1$) be two convex domains with areas $A_k$ and perimeters $P_k$. Denote by ${\mathrm{\Delta }}_2(K_k)=P_k^2-4\pi A_k$ the isoperimetric deficit of $K_k$. Then a sufficient condition for $t{K}_1$, a homothetic copy of the convex domain $K_1$, to contain domain $K_0$ for a translation and any rotation, is

$$t{P}_1-P_0>\sqrt{t^2{\mathrm{\Delta }}_2(K_1)+{\mathrm{\Delta }}_2(K_0)}.$$

(15)

Proof Condition (15) means that $t{P}_1>P_0$ and

$$2\pi A_1{t}^2-P_0{P}_{1}t+2\pi A_0>0.$$

(16)

By Theorem 1, we conclude that $t{K}_1$ either contains $K_0$ or is contained in $K_0$. This inequality also leads to

$$2\pi (t^2{A}_1-A_0)>t{P}_0{P}_1-4\pi A_0>P_0^2-4\pi A_0={\mathrm{\Delta }}_2(K_0).$$

The isoperimetric inequality guarantees that $t^2{A}_1>A_0$. We complete the proof of the theorem. □

3 Bonnesen-style mixed inequalities

Let $r_{01}=max\{t:t(g{K}_1)\subseteq K_0,g\in G_2\}$, the maximum inscribed radius of $K_0$ with respect to $K_1$, and $R_{01}=min\{t:t(g{K}_1)\supseteq K_0,g\in G_2\}$, the minimum circum scribed radius of $K_0$ with respect to $K_1$. Note that $r_{01}$, $R_{01}$ are, respectively, the maximum inscribed radius, the minimum circum radius of $K_0$ when $K_1$ is the unit disc. It is obvious that $r_{01}\le R_{01}$. Therefore, for $t\in [r_{01},R_{01}]$ neither $t{K}_1$ contains $K_0$ nor it is contained in $K_0$. Then by Theorem 1, we have the following.

Theorem 3 Let $K_k$ ($k=0,1$) be two convex domains with areas $A_k$ and perimeters $P_k$. Then

$$2\pi A_1{t}^2-P_0{P}_{1}t+2\pi A_0\le 0;r_{01}\le t\le R_{01}.$$

(17)

When $K_1$ is the unit disc, this reduces to the following known Bonnesen inequality (cf. [3, 9, 31, 36, 61]).

Corollary 1 Let K be a convex domain with a simple boundary ∂K of length P and area A. Denote by R and r, respectively, the radius of the minimum circumscribed disc and radius of the maximum inscribed disc of K. Then

$$\pi t^2-Pt+A\le 0;r\le t\le R.$$

(18)

By the two special cases of inequality (17):

$$2\pi A_1{r}_{01}^2-P_0{P}_1{r}_{01}+2\pi A_0\le 0;2\pi A_1{R}_{01}^2-P_0{P}_1{R}_{01}+2\pi A_0\le 0,$$

we obtain the following.

Theorem 4 Let $K_k$ ($k=0,1$) be two convex domains in the Euclidean plane $R^2$ with areas $A_k$ and perimeters $P_k$. If $K_1$ is convex, then

$$P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{A}_1^2{(R_{01}-r_{01})}^2+{[2\pi A_1(R_{01}+r_{01})-P_0{P}_1]}^2,$$

where the equality holds if and only if $r_{01}=R_{01}$, that is, $K_0$ and $K_1$ are discs.

Proof By inequalities (19), we have

$$\begin{array}{c}-8{\pi }^2{A}_0{A}_1\ge 8{\pi }^2{A}_1^2{r}_{01}^2-4\pi A_1{r}_{01}{P}_0{P}_1,-8{\pi }^2{A}_0{A}_1\ge 8{\pi }^2{A}_1^2{R}_{01}^2-4\pi A_1{R}_{01}{P}_0{P}_1,\hfill \\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge P_0^2{P}_1^2+8{\pi }^2{A}_1^2{r}_{01}^2+8{\pi }^2{A}_1^2{R}_{01}^2-4\pi A_1{r}_{01}{P}_0{P}_1-4\pi A_1{R}_{01}{P}_0{P}_1.\hfill \end{array}$$

Since

$$\begin{array}{r}{P}_0^2{P}_1^2+8{\pi }^2{A}_1^2{r}_{01}^2+8{\pi }^2{A}_1^2{R}_{01}^2-4\pi A_1{r}_{01}{P}_0{P}_1-4\pi A_1{R}_{01}{P}_0{P}_1\\ =4{\pi }^2{A}_1^2{r}_{01}^2+4{\pi }^2{A}_1^2{R}_{01}^2-8{\pi }^2{A}_1^2{r}_{01}{R}_{01}\\ +P_0^2{P}_1^2+4{\pi }^2{A}_1^2{r}_{01}^2+4{\pi }^2{A}_1^2{R}_{01}^2+8{\pi }^2{A}_1^2{r}_{01}{R}_{01}-4\pi A_1{r}_{01}{P}_0{P}_1-4\pi A_1{R}_{01}{P}_i{P}_j\\ =4{\pi }^2{A}_1^2{(R_{01}-r_{01})}^2+{(2\pi A_1{r}_{01}+2\pi A_1{R}_{01}-P_0{P}_1)}^2,\end{array}$$

therefore,

$$P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{A}_1^2{(R_{01}-r_{01})}^2+{[2\pi A_1(r_{01}+R_{01})-P_0{P}_1]}^2.$$

We complete the proof of Theorem 4. □

The following Kotlyar’s inequality (cf. [3, 24]) is an immediate consequence of Theorem 4.

Corollary 2 (Kotlyar)

Let $K_k$ ($k=0,1$) be two domains in $R^2$ with areas $A_k$ and perimeters $P_k$. If $K_1$ is convex, then

$$P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{A}_1^2{(R_{01}-r_{01})}^2,$$

(19)

where the equality holds if and only if both $K_0$ and $K_1$ are discs.

Let $K_1$ be the unit disc, then Theorem 4 immediately leads to the following inequality that strengthens the Bonnesen isoperimetric inequality (4).

Corollary 3 Let K be a domain of area A, bounded by a simple closed curve of length P in the Euclidean plane $R^2$. Let r and R be, respectively, the inscribed radius and circumscribed radius of K, then

$$P^2-4\pi A\ge {\pi }^2{(R-r)}^2+{[\pi (R+r)-P]}^2,$$

(20)

where the equality holds if and only if K is a disc.

One immediate consequence of Theorem 4 is the following mixed isoperimetric inequality:

$$P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 0,$$

where the equality holds if and only if $K_0$ and $K_1$ are discs.

One may wish to consider the following Bonnesen-style mixed inequality:

$$P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge B_{K_0,K_1},$$

where $B_{K_0,K_1}$ is an invariant of $K_0$ and $K_1$. $B_{K_0,K_1}$ is, of course, assumed to be nonnegative and vanishes only when both $K_0$ and $K_1$ are discs.

The inequality (17) can be rewritten as the following several inequalities:

$$\begin{array}{r}{P}_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(P_0{P}_1-4\pi A_{1}t)}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(P_0{P}_1-\frac{4\pi A_0}{t})}^2;r_{01}\le t\le R_{01},\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{(\frac{A_0}{t}-A_{1}t)}^2,\end{array}$$

(21)

Therefore, we obtain the following Bonnesen-style mixed inequalities.

Corollary 4 Let $K_k$ ($k=0,1$) be two convex domains in the Euclidean plane $R^2$ with areas $A_k$ and perimeters $P_k$. Then for $r_{01}\le t\le R_{01}$, we have

$$\begin{array}{r}{P}_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{A}_1^2{(R_{01}-t)}^2+{[2\pi A_1(t+R_{01})-P_0{P}_1]}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{A}_1^2{(t-r_{01})}^2+{[2\pi A_1(r_{01}+t)-P_0{P}_1]}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(P_0{P}_1-4\pi A_1{r}_{01})}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(\frac{4\pi A_0}{r_{01}}-P_0{P}_1)}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{(\frac{A_0}{r_{01}}-A_1{r}_{01})}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(P_0{P}_1-4\pi A_{1}t)}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(P_0{P}_1-\frac{4\pi A_0}{t})}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{(\frac{A_0}{t}-A_{1}t)}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(4\pi A_1{R}_{01}-P_0{P}_1)}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge {(P_0{P}_1-\frac{4\pi A_0}{R_{01}})}^2;\\ P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 4{\pi }^2{(A_1{R}_{01}-\frac{A_0}{R_{01}})}^2.\end{array}$$

(22)

Each inequality holds as an equality if and only if both $K_0$ and $K_1$ are discs.

On the other hand, let us consider the following Bonnesen quadratic polynomial

$$B_{K_0,K_1}(t)=2\pi A_1{t}^2-P_0{P}_{1}t+2\pi A_0.$$

It is clear that $B_{K_0,K_1}(0)>0$ and $B_{K_0,K_1}(+\mathrm{\infty })>0$. If $K_1$ is convex, then the mixed isoperimetric inequality guarantees that two roots $\frac{P_0{P}_1\pm \sqrt{{\mathrm{\Delta }}_2(K_0,K_1)}}{4\pi A_1}$ of $B_{K_0,K_1}(t)=0$ exist and satisfy

$$0<\frac{P_0{P}_1-\sqrt{{\mathrm{\Delta }}_2(K_0,K_1)}}{4\pi A_1}\le r_{01}\le R_{01}\le \frac{P_0{P}_1+\sqrt{{\mathrm{\Delta }}_2(K_0,K_1)}}{4\pi A_1}<+\mathrm{\infty }.$$

(23)

The condition for existence of root(s) of the Bonnesen quadratic equation $B_{K_0,K_1}(t)=0$ is the following symmetric mixed isoperimetric inequality:

$${\mathrm{\Delta }}_2(K_0,K_1)=P_0^2{P}_1^2-16{\pi }^2{A}_0{A}_1\ge 0.$$

(24)

The Bonnesen function $B_{K_0,K_1}(t)=2\pi A_1{t}^2-P_0{P}_{1}t+2\pi A_0$ attains minimum value $-\frac{{\mathrm{\Delta }}_2(K_0,K_1)}{8\pi A_1}$ at $t=\frac{P_0{P}_1}{4\pi A_1}$. The Bonnesen quadratic trinomial has only one root when ${\mathrm{\Delta }}_2(K_0,K_1)=0$. This means that both $K_0$ and $K_1$ are discs. This immediately leads to the following results.

Theorem 5 Let $K_k$ ($k=0,1$) be two convex domains of areas $A_k$ and perimeters $P_k$ in $R^2$. Then

$$2\pi A_1{t}^2-P_0{P}_{1}t+2\pi A_0\ge -\frac{{\mathrm{\Delta }}_2(K_0,K_1)}{8\pi A_1}.$$

(25)

Theorem 6 Let $K_k$ ($k=0,1$) be two convex domains of areas $A_k$ and perimeters $P_k$ in the Euclidean plane $R^2$. Then we have

$$\frac{P_0{P}_1-\sqrt{{\mathrm{\Delta }}_2(K_0,K_1)}}{4\pi A_1}\le r_{01}\le \frac{P_0{P}_1}{4\pi A_1}\le R_{01}\le \frac{P_0{P}_1+\sqrt{{\mathrm{\Delta }}_2(K_0,K_1)}}{4\pi A_1}.$$

(26)

Each equality holds if and only if $K_0$ and $K_1$ are discs.

The following known Bonnesen-style inequalities are immediate consequences of Corollary 4, Theorem 5 and Theorem 6 when letting $K_1$ be the unit disc (cf. [3, 9, 12, 23, 31, 32, 36, 58, 62]).

Corollary 5 Let K be a plane domain of area A, bounded by a simple closed curve of length P. Let r and R be, respectively, the in-radius and out-radius of K. Then for any disc of radius t, $r\le t\le R$, we have the following Bonnesen-style inequalities:

$$\begin{array}{r}{P}^2-4\pi A\ge {(P-2\pi t)}^2;\\ P^2-4\pi A\ge {\pi }^2{(t-r)}^2+{[\pi (t+r)-P]}^2;\\ P^2-4\pi A\ge {\pi }^2{(R-t)}^2+{[\pi (R+t)-P]}^2;\\ P^2-4\pi A\ge {(P-\frac{2A}{t})}^2;P^2-4\pi A\ge {(\frac{A}{t}-\pi t)}^2;\\ P^2-4\pi A\ge A^2{(\frac{1}{r}-\frac{1}{R})}^2;P^2-4\pi A\ge P^2{\left(\frac{R-r}{R+r}\right)}^2;\\ P^2-4\pi A\ge A^2{(\frac{1}{r}-\frac{1}{t})}^2;P^2-4\pi A\ge P^2{\left(\frac{t-r}{t+r}\right)}^2;\\ P^2-4\pi A\ge A^2{(\frac{1}{t}-\frac{1}{R})}^2;P^2-4\pi A\ge P^2{\left(\frac{R-t}{R+t}\right)}^2;\\ \frac{P-\sqrt{P^2-4\pi A}}{2\pi }\le r\le t\le R\le \frac{P+\sqrt{P^2-4\pi A}}{2\pi }.\end{array}$$

(27)

Each equality holds if and only if K is a disc.

It should be noted that the first inequality in (27) is due to Bonnesen, and he only derived some inequalities for 2-dimensional case and never had any progress for higher dimensions or 2-dimensional surface of constant curvature. One would be interested in the situations in higher dimensional space $R^n$ and in the surface of constant curvature. Related development in those areas can be found in [26, 35, 37, 63–66] and [58]. More details for the isoperimetric inequality and Bonnesen style inequalities can be found in [67–80].