Abstract
Let be the skew-adjacency matrix of an oriented graph with n vertices, and let be all eigenvalues of . The skew-spectral radius of is defined as . A connected graph, in which the number of edges equals the number of vertices, is called a unicyclic graph. In this paper, the structure of oriented unicyclic graphs whose skew-spectral radius does not exceed 2 is investigated. We order all the oriented unicyclic graphs with n vertices whose skew-spectral radius is bounded by 2.
MSC:05C50, 15A18.
Similar content being viewed by others
1 Introduction
Let G be a simple graph with n vertices. The adjacency matrix is the symmetric matrix , where if is an edge of G, otherwise, . We call the characteristic polynomial of G, denoted by (or abbreviated to ). Since A is symmetric, its eigenvalues are real, and we assume that . We call the adjacency spectral radius of G.
The class of all graphs G whose largest (adjacency) spectral radius is bounded by 2 has been completely determined by Smith; see, for example, [1, 2]. Later, Hoffman [3], Cvetković et al. [4] gave a nearly complete description of all graphs G with (≈2.0582). Their description was completed by Brouwer and Neumaier [5]. Then Woo and Neumaier [6] investigated the structure of graphs G with (≈2.1312), Wang et al. [7] investigated the structure of graphs whose largest eigenvalue is close to .
Another interesting problem that arises in the context of graph eigenvalues is to order graphs in some class with respect to the spectral radius or least eigenvalue. In 2003, Guo [8] gave the first six unicyclic graphs of order n with larger spectral radius. Belardo et al. [9] ordered graphs with spectral radius in the interval . In the paper [10], the first five unicyclic graphs on order n in terms of their smaller least eigenvalues were determined.
The graph obtained from a simple undirected graph by assigning an orientation to each of its edges is referred as the oriented graph. Let be an oriented graph with vertex set and edge set . The skew-adjacency matrix related to is defined as

where  (note that the definition is slightly different from the one of the normal skew-adjacency matrix given by Adiga et al. [11]). Since is an Hermitian matrix, the eigenvalues of are all real numbers and, thus, can be arranged non-increase as
(note that the definition is slightly different from the one of the normal skew-adjacency matrix given by Adiga et al. [11]). Since is an Hermitian matrix, the eigenvalues of are all real numbers and, thus, can be arranged non-increase as
The skew-spectral radius and the skew-characteristic polynomial of are defined respectively as
and
Recently, much attention has been devoted to the skew-adjacency matrix of an oriented graph. In 2009, Shader and So [12] investigated the spectra of the skew-adjacency matrix of an oriented graph. In 2010, Adiga et al. [11] discussed the properties of the skew-energy of an oriented graph. In papers [13, 14], all the coefficients of the skew-characteristic polynomial of in terms of G were interpreted. Cavers et al. [15] discussed the graphs whose skew-adjacency matrices are all cospectral, and the relations between the matchings polynomial of a graph and the characteristic polynomials of its adjacency and skew-adjacency matrices. In [16], the author established a relation between and . Also, the author gave some results on the skew-spectral radii of and its oriented subgraphs.
A connected graph in which the number of edges equals the number of vertices is called a unicyclic graph. In this paper, we will investigate the skew-spectral radius of an oriented unicyclic graph. The rest of this paper is organized as follows: In Section 2, we introduce some notations and preliminary results. In Section 3, all the oriented unicyclic graphs whose skew-spectral radius does not exceed 2 are determined. The result tells us that there is a big difference between the (adjacency) spectral radius of an undirected graph and the skew-spectral radius of its corresponding oriented graph. Furthermore, we order all the oriented unicyclic graphs with n vertices whose skew-spectral radius is bounded by 2 in Section 4.
2 Preliminaries
Let be a simple graph with vertex set and . Denote by the graph obtained from G by deleting the edge e and by the graph obtained from G by removing the vertex v together with all edges incident to it. For a nonempty subset W of , the subgraph with vertex set W and edge set consisting of those pairs of vertices that are edges in G is called an induced subgraph of G. Denote by , and the cycle, the star and the path on n vertices, respectively. Certainly, each subgraph of an oriented graph is also referred as an oriented graph and preserves the orientation of each edge.
Recall that the skew-adjacency matrix of any oriented graph is Hermitian, then the well-known interlacing theorem for Hermitian matrices applies equally well to oriented graphs; see, for example, Theorem 4.3.8 of [17].
Lemma 2.1 Let be an arbitrary oriented graph on n vertices and . Suppose that . Then
Let be an oriented graph, and let () be a cycle of G, where adjacent to for and adjacent to . Let also be the skew-adjacency matrix of whose first k rows and columns correspond to the vertices . The sign of the cycle , denoted by , is defined by
Let be the cycle by inverting the order of the vertices along the cycle C. Then one can verify that
Moreover, is either 1 or −1 if the length of C is even; and is either  or
or  if the length of C is odd. For an even cycle, we simply refer it as a positive cycle or a negative cycle according to its sign. A positive even cycle is also named as oriented uniformly by Hou et al. [14].
if the length of C is odd. For an even cycle, we simply refer it as a positive cycle or a negative cycle according to its sign. A positive even cycle is also named as oriented uniformly by Hou et al. [14].
On the skew-spectral radius of an oriented graph, we have obtained the following results. They will be useful in the proofs of the main results of this paper.
Lemma 2.2 ([[16], Theorem 2.1])
Let be an arbitrary connected oriented graph. Denote by the (adjacency) spectral radius of G. Then
with equality if and only if G is bipartite and each cycle of G is a positive even cycle.
Lemma 2.3 ([[16], Theorem 3.2])
Let be a connected oriented graph. Suppose that each even cycle of G is positive. Then
-
(a)
for any ;
-
(b)
for any .
Lemma 2.4 ([[14], Theorem 2.4], [[16], Theorem 3.1])
Let be an oriented graph, and let be its skew-characteristic polynomial. Then
where the first summation is over all the vertices in , and the second summation is over all even cycles of G containing the vertex u,
where and the summation is over all even cycles of G containing the edge e, and denotes the sign of the even cycle C.
Lemma 2.5 ([[13], A part of Theorem 2.5])
Let be an oriented graph, and let be its skew-characteristic polynomial. Then
where denotes the derivative of .
Finally, we introduce a class of undirected graphs that will be often mentioned in this manuscript.
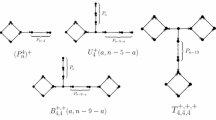
Denote by a pathlike graph, which is defined as follows: we first draw k (≥2) paths of orders respectively along a line and put two isolated vertices between each pair of those paths, then add edges between the two isolated vertices and the nearest end vertices of such a pair of paths such that the four newly added edges form a cycle , where and for . Then contains vertices. Notice that if (), the two end vertices of the path are referred as overlap; if (), the left (right) of the graph has only two pendent vertices. Obviously, , the star of order 3, and . In general, , , are all unicyclic graphs containing , where .
3 The oriented unicyclic graphs whose skew-spectral radius does not exceed 2
In this section, we determine all the oriented unicyclic graphs whose skew-spectral radius does not exceed 2.
First, we introduce more notations. Denote by the starlike tree with exactly one vertex v of degree 3, and , where is the path of order ().
Due to Smith, all undirected graphs whose (adjacency) spectral radius is bounded by 2 are completely determined as follows.
Lemma 3.1 ([2] or [[1], Chapter 2.7.12])
All undirected graphs whose spectral radius does not exceed 2 are , , , , and their subgraphs, where and .
By Lemma 2.4, to study the skew-spectrum properties of an oriented graph, we need only consider the sign of those even cycles. Moreover, Shader and So showed that has the same spectrum as that of its underlying tree for any oriented tree ; see Theorem 2.5 of [12]. Consequently, combining with Lemma 2.2, the skew-spectral radius of each oriented graph whose underlying graph is as described in Lemma 3.1, regardless of the orientation of the oriented cycle , does not exceed 2.
For convenience, we write:
.
.
.
.
Moreover, let be a cycle on m vertices, and let be m paths with lengths (perhaps some of them are empty), respectively. Denote by the unicyclic undirected graph obtained from by joining to a pendent vertex of for . Suppose, without loss of generality, that , , and write instead of the standard if .
By Lemmas 2.2 and 2.4 or papers [11, 12], for a given unicyclic graph , we know that the skew-spectral radius of is independent of its orientation if m is odd. Therefore, we will briefly write instead of the normal notation if each cycle of G is odd. If m is even, then essentially, there exist two orientations (the sign of the even cycle is positive) and (the sign of the even cycle is negative) such that and . Henceforth, we will briefly write (or ) instead of if the sign of each even cycle is negative (or positive). In particular, G will also denote the oriented graph if G is a tree since in this case.
3.1 The -free oriented unicyclic graphs whose skew-spectral radius does not exceed 2
Let be an oriented graph with the property
The property (3.1) is hereditary, because, as a direct consequence of Lemma 2.1, for any induced subgraph , also satisfies (3.1). The inheritance (hereditary) of property (3.1) implies that there are minimal connected graphs that do not obey (3.1); such graphs are called forbidden subgraphs. It is easy to verify the following.
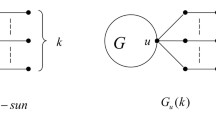
Lemma 3.2 Let with . Then , , , , , are forbidden, where (or ) denotes the oriented graph obtained by adding two pendent vertices to a vertex (or the pendent vertex) of (or ).
Combining with Lemma 3.2 and the fact that if the oriented tree T contains an arbitrary tree described as Lemma 3.1 as a proper subgraph, we have the following result.
Theorem 3.1 Let and . Let also . Then is one of , , , and their induced oriented unicyclic subgraphs.
Proof Denote by the girth of G. Let and be the cycle of G with vertex set such that adjacent to for and adjacent to . (We should point out once again that in (), we always refer adjacent to one pendent vertex of , a path with length , for .) We divide our proof into the following four claims.
Claim 1 If , then .
The result follows from Lemma 3.2 that , and , are forbidden.
Claim 2 If , then . Moreover, each induced even cycle of is negative.
Let . Notice that G is -free, then if , and, thus, G contains the induced subgraph as . From Lemma 3.2, both and are forbidden, thus, . Moreover, the graph obtained from by deleting the vertex is the tree for . Thus, there is an induced subgraph if , which is a contradiction to Lemma 3.1. Hence, the former follows.
Assume to the contrary that there exists a positive even cycle , then by Lemma 2.3, , a contradiction. Thus, the latter follows.
Claim 3 If , then is one of , or their induced subgraphs.
By Claim 2, we always suppose that each cycle is negative.
We first claim that G is of , that is, each pendent tree adjacent to of is a path for . Otherwise, assume that the pendent tree adjacent to is not a path, then the resultant graph by deleting vertex of G is a tree and contains the tree as a proper induced subgraph, and, thus, combining with Lemmas 2.3 and 3.2, a contradiction. Moreover, we have . Otherwise, contains as an induced subgraph. Notice that both and are trees and contain as a proper induced subgraph, then G may be and . By calculation, we have and . Thus, the result follows.
Claim 4 If , then is one of or its induced subgraphs.
By Claim 2, the cycle of is negative. Notice that , , , , each of them has skew-spectral radius greater than 2. Then may be . By calculation, we have . Thus, the result follows. □
3.2 The oriented unicyclic graphs in whose skew-spectral radius does not exceed 2
Now, we consider the oriented unicyclic graphs in . First, we have the following.
Lemma 3.3 Let . Then
-
(a)
;
-
(b)
.
Proof (a) Let . We first show by induction on n that
Let . Then there is exactly one pathlike graph if , namely, . By calculation, we have
Suppose now that , and the result is true for the order no more than . Applying Lemma 2.4 to the left pendent vertex of , we have
Then by induction hypothesis, and, thus, the result follows.
Let now v be a vertex with degree 2 in of . Then , a path of order . Let and be all eigenvalues of and , respectively. By Lemma 2.1 and the fact that , we have . On the other hand, we have
Consequently, , and, thus, by Eq. (3.2). Thus, the result (a) holds.
-
(b)
We first show that 2 is an eigenvalue of .
By the proof of the result (a), we know that
It tells us that
Note that . We know that .
Now, we show that 2 is also an eigenvalue of . Applying Lemma 2.5, we have
It is easy to see that 2 is an eigenvalue of each oriented graph . Thus, 2 is an eigenvalue of with multiplicity 2. □
By calculation, we have the following.
Lemma 3.4 Let with . Then () are forbidden, where , , , , , and , which denotes the graph obtained by adding a pendent vertex to a vertex of .
Combining with Lemma 3.4 and the fact that if the oriented tree T contains an arbitrary tree described as Lemma 3.1 as a proper subgraph, we have the following result.
Theorem 3.2 Let and . Then is one of , , , and or their induced oriented unicyclic subgraphs.
Proof Note that the induced cycle of must be negative. By Lemma 3.3, we can assume that .
Case 1. .
Then G contains an induced tree T such that T has a proper induced subgraph . It means that , a contradiction.
Case 2. .
Then, by Lemma 3.4, we know that and . Thus, it is not difficult to see that the possible oriented graphs are , , , or their induced oriented unicyclic subgraphs by Lemma 3.4. Moreover, taking some computations, we know the skew-spectral radius of each above oriented graph does not exceed 2.
Combining with Lemma 3.3, the result follows. □
3.3 The oriented unicyclic graphs whose skew-spectral radius does not exceed 2
Putting Lemma 3.1 together with Theorem 3.1 and Theorem 3.2, we have the following.
Theorem 3.3 Let and . Then is one of , , , , , , , , and or their induced oriented unicyclic subgraphs, where the orientation of is arbitrary.
Moreover, by calculation, we have the following two corollaries from Theorem 3.3.
Corollary 3.1 Let and . Then is one of the following oriented graphs.
-
(a)
, where m is even;
-
(b)
, , where ;
-
(c)
, , , , , , , , , , and .
Corollary 3.2 Let and . Then is one of the following oriented graphs or their induced oriented unicyclic subgraphs.
-
(a)
, where m is odd, or m is even, and the sign of is negative;
-
(b)
, where ;
-
(c)
, , , , , .
4 Ordering the oriented unicyclic graphs whose skew-spectral radius is bounded by 2
In this section, we discuss the skew-spectral radii of oriented unicyclic graphs in . Let and . By Corollary 3.2, we know that is (where n is odd, or n is even, and the sign is negative) or (where ) if . This makes it possible to order the oriented unicyclic graphs whose skew-spectral radius is bounded by 2.
Lemma 4.1 Let . Then .
Proof By Lemma 2.4, we have
Thus,
Moreover, we have
where . It is easy to know that
and
Similarly, we have
Hence,
Let . Then for , we have
Obviously, the above equality also holds for . It means that , since . Thus, . □
By Lemma 4.1, we know that
Now, we need only to compare the skew-spectral radii of and . In fact, we have the following.
Lemma 4.2 Let . Then we have
-
(a)
if n is odd;
-
(b)
if n is even.
Proof Note that by paper [11]
Moreover, we have . Thus, if n is odd.
On the other hand, we have
Thus,
It means that . Then the result (a) follows.
If n is even, then let . We have
Thus,
Then the result (b) holds. □
By Lemmas 4.1 and 4.2, we obtain the following interesting result.
Theorem 4.1 Let be an oriented unicyclic graph on order n (). , , where and if n is even. Then
-
(a)
if n is odd;
-
(b)
if n is even.
Combining with Corollary 3.1, we have ordered all the oriented unicyclic graphs with n vertices whose skew-spectral radius is bounded by 2.
References
Cvetković D, Doob M, Sachs H: Spectra of Graphs. Academic Press, New York; 1980.
Smith JH: Some properties of the spectrum of a graph. In Combinatorial Structures and Their Applications. Edited by: Guy R. Gordon & Breach, New York; 1970:403–406.
Hoffman A: On limit points of spectral radii of non-negative symmetrical integral matrices. Lecture Notes in Math. 303. Graph Theory and Applications 1972, 165–172.
Cvetković D, Doob M, Gutman I:On graphs whose spectral radius does not exceed . Ars Comb. 1982, 14: 225–239.
Brouwer AE, Neumaier A:The graphs with largest eigenvalue between 2 and . Linear Algebra Appl. 1989, 114/115: 273–276.
Woo R, Neumaier A:On graphs whose spectral radius is bounded by . Graphs Comb. 2007, 23: 713–726. 10.1007/s00373-007-0745-9
Wang JF, Huang QX, An XH, Belardo F:Some notes on graphs whose spectral radius is close to . Linear Algebra Appl. 2008, 429: 1606–1618. 10.1016/j.laa.2008.04.034
Guo SG: The first six unicyclic graphs of order n with larger spectral radius. Appl. Math. J. Chin. Univ. Ser. A 2003, 18(4):480–486. (in Chinese)
Belardo F, Li Marzi EM, Simić SK:Ordering graphs with index in the interval . Discrete Appl. Math. 2008, 156: 1670–1682. 10.1016/j.dam.2007.08.027
Xu GH: Ordering unicyclic graphs in terms of their smaller least eigenvalues. J. Inequal. Appl. 2010., 2010: Article ID 591758
Adiga C, Balakrishnan R, So WS: The skew energy of a graph. Linear Algebra Appl. 2010, 432: 1825–1835. 10.1016/j.laa.2009.11.034
Shader B, So WS: Skew spectra of oriented graphs. Electron. J. Comb. 2009., 16: Article ID N32
Gong SC, Xu GH: The characteristic polynomial and the matchings polynomial of a weighted oriented graph. Linear Algebra Appl. 2012, 436: 465–471. 10.1016/j.laa.2011.03.067
Hou YP, Lei TG: Characteristic polynomials of skew-adjacency matrices of oriented graphs. Electron. J. Comb. 2011., 18: Article ID P156
Cavers M, Cioabǎ SM, Fallat S, Gregory DA, Haemerse WH, Kirkland SJ, McDonald JJ, Tsatsomeros M: Skew-adjacency matrices of graphs. Linear Algebra Appl. 2012, 436: 4512–4529. 10.1016/j.laa.2012.01.019
Xu GH: Some inequalities on the skew-spectral radii of oriented graphs. J. Inequal. Appl. 2012., 2012: Article ID 211
Horn R, Johnson C: Matrix Analysis. Cambridge University Press, Cambridge; 1989.
Acknowledgements
The authors are grateful to the referees for their valuable comments and suggestions, which led to a great improvement of the original manuscript. This work was supported by the National Natural Science Foundation of China (No. 11171373), the Zhejiang Provincial Natural Science Foundation of China (LY12A01016).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
PC carried out the studies of the skew-spectral radii and drafted the manuscript. GX conceived of the study and finished the final manuscript. LZ participated in the design of the study and some calculation. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chen, PF., Xu, GH. & Zhang, LP. Ordering the oriented unicyclic graphs whose skew-spectral radius is bounded by 2. J Inequal Appl 2013, 495 (2013). https://doi.org/10.1186/1029-242X-2013-495
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-495