A certain class of analytic functions and the growth rate of Hankel determinant

Abstract

The growth rate of coefficients and Hankel determinant for any class of analytic functions is well known. In this present investigation, we define a class of analytic functions related to strongly close-to-convex functions. We investigate different interesting properties for this class including arc length, the growth rate of coefficients and the growth rate of Hankel determinant by using the method of Noonan and Thomas. Several well-known results appear as special cases from our results.

MSC:30C45, 30C50.

1 Introduction

We denote by A the class of functions f which are analytic in the open unit disc $E=\{z:|z|<1\}$ and of the form

$$f(z)=z+\sum _{n=2}^{\mathrm{\infty }}{a}_n{z}^n.$$

(1.1)

Also let us denote by $P_k(\rho )$ the class of functions h with $h(0)=1$, which are analytic in E and satisfying

$${\int }_0^{2\pi }|Re\left\{\frac{h(z)-\rho }{1-\rho }\right\}|d\theta \le k\pi ,$$

where $z=r{e}^{i\theta }$, $k\ge 2$ and $0\le \rho <1$. This class has been investigated by Padmanabhan and Parvatham [1]. For $\rho =0$, we obtain the class $P_k$, introduced by Pinchuk [2] and for $\rho =0$, $k=2$, we obtain the class P of functions with a positive real part.

The class $T_k$ was first introduced and investigated by the second author [3] as a generalization of close-to-convexity. She studied its geometrical interpretation and various other interesting properties including the growth rate of coefficient differences and a radius of convexity problem. Recently, she [4] studied the class of analytic functions corresponding to strongly close-to-convex functions. She employed a modification to a method of Pommerenke [5] to investigate the growth rate of Hankel determinant problems regarding this class.

In this paper, we define a class of analytic functions related to strongly close-to-convex functions. We investigate different interesting properties including inclusion relations, arc length, the growth rate of coefficients and the growth rate of Hankel determinant by using a different method from that given in [4].

We now define the following classes of analytic functions.

Definition 1.1 Let $f\in A$ be locally univalent in E. Then, for $\eta \ne 0$ (complex), $0\le \rho <1$, $f\in V_k(\eta ,\rho )$ if and only if

$$(1+\frac{1}{\eta }\frac{z{f}^{\mathrm{\prime }\mathrm{\prime }}(z)}{f^{\mathrm{\prime }}(z)})\in P_k(\rho ),z\in E.$$

We note that for $\eta =1$, we have the class $V_k(\rho )$ of bounded boundary rotations of order ρ introduced by Padmanabhan and Parvatham [1]. Also, $V_k(0)=V_k$, the class of functions of bounded boundary rotations and $V_2(\eta ,0)=C(\eta )$ denotes the class of convex functions of complex order.

Definition 1.2 Let $f\in A$. Then $f\in {\tilde{N}}_k(\eta ,\rho ,\beta )$ if and only if, for $k\ge 2$, $\beta \ge 0$, there exists a function $g\in V_k(\eta ,\rho )$ such that

$$|arg\frac{f^{\mathrm{\prime }}(z)}{g^{\mathrm{\prime }}(z)}|\le \frac{\beta \pi }{2},z\in E.$$

For $\eta =1$, we have the class ${\tilde{T}}_k(\rho ,\beta )$ which was recently introduced and studied by Noor [4]. For $k=2$, $\eta =1$, $\rho =0$, ${\tilde{N}}_2(1,0,\beta )$ is the class of strongly close-to-convex functions. Also, ${\tilde{N}}_2(1,\rho ,0)=C(\rho )$ is the class of convex functions of order ρ. For $\eta =1$, $\rho =0$, $\beta =1$, the class of ${\tilde{N}}_k(\eta ,\rho ,\beta )$ reduces to the class $T_k$ introduced by Noor [3].

We need the following results in our investigation.

Lemma 1.1 A function $f\in V_k(\eta ,\rho )$ if and only if

• (i) $f^{\mathrm{\prime }}(z)={[f_1^{\mathrm{\prime }}(z)]}^{(1-\rho )\eta }$, $f_1(z)\in V_k$,

• (ii) $f^{\mathrm{\prime }}(z)={[f_2^{\mathrm{\prime }}(z)]}^{\eta }$, $f_1(z)\in V_k(\rho )$,

• (iii) there exist two normalized starlike functions $s_1(z)$ and $s_2(z)$ such that

  

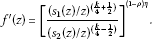  (1.2)

The above lemma is a special case of the result discussed in [6].

Lemma 1.2 [7]

Let $h\in P$ with $z=r{e}^{i\theta }$. Then

$$\frac{1}{2\pi }{\int }_0^{2\pi }|h(z){|}^{2}d\theta \le \frac{1+3r^2}{1-r^2}.$$

Lemma 1.3 [8]

Let f be univalent and $0\le r<1$. Then there exists a number $z_1$ with $|z_1|=r$, such that for all z, $|z|=r$, we have

$$|z-z_1||f(z)|\le \frac{2r^2}{1-r^2}.$$

2 Some properties of the class ${\tilde{N}}_k(\eta ,\rho ,\beta )$

Following essentially the same method as given in [4], we can easily obtain the following result.

Theorem 2.1 The function $f\in {\tilde{N}}_k(\eta ,\rho ,\beta )$ if and only if

$$f^{\mathrm{\prime }}(z)=\frac{{(f_1(z))}^{(\frac{k}{4}+\frac{1}{2})(1-\rho )\eta }}{{(f_2(z))}^{(\frac{k}{4}-\frac{1}{2})(1-\rho )\eta }},$$

where $f_1$ and $f_2$ are strongly close-to-convex functions of order β.

Theorem 2.2 Let $f\in {\tilde{N}}_k(\eta ,\rho ,\beta )$ in E. Then $f\in C_{\eta }$ for $|z|<r_0$, where

$$r_0=\frac{2|\eta |}{[(1-\rho )|\eta |k+2\beta ]+\sqrt{{[(1-\rho )|\eta |k+2\beta ]}^2-4(1-2\rho )|\eta {|}^2}}.$$

(2.1)

This result is sharp.

Proof We can write

$$f^{\mathrm{\prime }}(z)=g^{\mathrm{\prime }}(z)h^{\beta }(z),g(z)\in V_k(\eta ,\rho ),h(z)\in P.$$

Using Lemma 1.1, we have

(2.2)

where $s_1$ and $s_2$ are starlike functions. Logarithmic differentiation of (2.2) gives us

$$\frac{z{f}^{\mathrm{\prime }\mathrm{\prime }}(z)}{f^{\mathrm{\prime }}(z)}=(1-\rho )\eta [-1+(\frac{k}{4}+\frac{1}{2})\frac{z{s}_1^{\mathrm{\prime }}(z)}{s_1(z)}-(\frac{k}{4}-\frac{1}{2})\frac{z{s}_2^{\mathrm{\prime }}(z)}{s_2(z)}]+\beta \frac{z{h}^{\mathrm{\prime }}(z)}{h(z)},$$

which implies that

$$1+\frac{1}{\eta }\frac{z{f}^{\mathrm{\prime }\mathrm{\prime }}(z)}{f^{\mathrm{\prime }}(z)}=\rho +(1-\rho )[(\frac{k}{4}+\frac{1}{2})\frac{z{s}_1^{\mathrm{\prime }}(z)}{s_1(z)}-(\frac{k}{4}-\frac{1}{2})\frac{z{s}_2^{\mathrm{\prime }}(z)}{s_2(z)}]+\frac{\beta }{\eta }\frac{z{h}^{\mathrm{\prime }}(z)}{h(z)}.$$

Now using distortion results for the class P, we have

$$\begin{array}{rcl}Re(1+\frac{1}{\eta }\frac{z{f}^{\mathrm{\prime }\mathrm{\prime }}(z)}{f^{\mathrm{\prime }}(z)})& \ge & \rho +(1-\rho )[(\frac{k}{4}+\frac{1}{2})\frac{1-r}{1+r}-(\frac{k}{4}-\frac{1}{2})\frac{1+r}{1-r}]-\frac{\beta }{|\eta |}\frac{2r}{1-r^2}\\ =& \frac{\rho |\eta |(1-r^2)+(1-\rho )|\eta |[1-kr+r^2]-2\beta r}{|\eta |(1-r^2)}.\end{array}$$

(2.3)

The right-hand side of (2.3) is positive for $|z|<r_0$, where $r_0$ is given by (2.1). The sharpness can be viewed from the function $f_0\in {\tilde{N}}_k(\eta ,\rho ,\beta )$, given by

$$f_0^{\mathrm{\prime }}(z)=\frac{{(1+z)}^{(\frac{k}{2}-1)(1-\rho )\eta +\beta }}{{(1-z)}^{(\frac{k}{2}+1)(1-\rho )\eta +\beta }},z\in E.$$

(2.4)

We note the following.

• (i) For $\eta =1$, we have the radius of convexity for the class $\widetilde{T_k}(\rho ,\beta )$ studied by Noor [4].

• (ii) For $\eta =1$, $\rho =0$, $\beta =1$, we have the radius of convexity for the class $T_k$, proved by Noor [3].

• (iii) For $\eta =1$, $\rho =0$, $\beta =1$, $k=2$, we have the radius of convexity for close-to-convex functions which is well known.

 □

We now discuss the arc length problem and the growth rate of coefficients for the class $\widetilde{N_k}(\eta ,\rho ,\beta )$.

Theorem 2.3 Let $f\in \widetilde{N_k}(\eta ,\rho ,\beta )$, for $Re\eta >0$, $\beta \ge 0$, $0\le \rho <1$ and $\frac{(k+2)(1-\rho )Re\eta }{2-\beta }>1$. Then

$$L_r(f)\le c(k,\eta ,\rho ,\beta ){\left(\frac{1}{1-r}\right)}^{(\frac{k}{2}+1)(1-\rho )Re\eta +\beta -1},$$

where $c(k,\eta ,\rho ,\beta )$ is a constant depending only on k, η, ρ, β. The exponent $[(\frac{k}{2}+1)(1-\rho )Re\eta +\beta -1]$ is sharp.

Proof We have

$$L_r(f)={\int }_0^{2\pi }|z{f}^{\mathrm{\prime }}(z)|d\theta ,z=r{e}^{i\theta }.$$

Using Definition 1.1, Lemma 1.1(iii) and the distortion theorem for starlike functions, we have

$$\begin{array}{rcl}{L}_r(f)& =& {\int }_0^{2\pi }|z{g}^{\mathrm{\prime }}(z)h^{\beta }(z)|d\theta ,g(z)\in V_k(\eta ,\rho ),h(z)\in P\\ =& {\int }_0^{2\pi }\left|z\frac{{(s_1(z)/z)}^{(\frac{k}{4}+\frac{1}{2})(1-\rho )\eta }}{{(s_2(z)/z)}^{(\frac{k}{4}-\frac{1}{2})(1-\rho )\eta }}\right||h^{\beta }(z)|d\theta \\ =& {\int }_0^{2\pi }\left|z^{1-\eta (1-\rho )}\frac{{(s_1(z))}^{(\frac{k}{4}+\frac{1}{2})(1-\rho )\eta }}{{(s_2(z))}^{(\frac{k}{4}-\frac{1}{2})(1-\rho )\eta }}\right||h^{\beta }(z)|d\theta \\ \le & \frac{2^{(\frac{k}{2}-1)(1-\rho )Re\eta }}{r^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -1}}{\int }_0^{2\pi }|s_1(z){|}^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta }|h(z){|}^{\beta }d\theta \\ \le & \frac{2^{(\frac{k}{2}-1)(1-\rho )Re\eta }}{r^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -1}}{\int }_0^{2\pi }{\left(\right|s_1(z){|}^{\frac{(\frac{k}{2}+1)(1-\rho )Re\eta }{2-\beta }})}^{\frac{2-\beta }{2}}{\left(\right|h(z){|}^2)}^{\frac{\beta }{2}}d\theta .\end{array}$$

Using Holder’s inequality with $p=\frac{2}{2-\beta }$, $q=\frac{2}{\beta }$ such that $\frac{1}{p}+\frac{1}{q}=1$, we obtain

$$\begin{array}{rcl}{L}_r(f)& \le & \frac{2^{(\frac{k}{2}-1)(1-\rho )Re\eta }}{r^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -1}}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }\right|s_1(z){|}^{\frac{(\frac{k}{2}+1)(1-\rho )Re\eta }{2-\beta }}d\theta )}^{\frac{2-\beta }{2}}\\ \times {\left(\frac{1}{2\pi }{\int }_0^{2\pi }\right|h(z){|}^{2}d\theta )}^{\frac{\beta }{2}}.\end{array}$$

Since $\frac{(k+2)(1-\rho )Re\eta }{2-\beta }>1$, therefore using subordination for starlike functions and Lemma 1.2, we have

$$\begin{array}{rcl}{L}_r(f)& \le & \frac{2^{(\frac{k}{2}-1)(1-\rho )Re\eta }}{r^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -1}}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }\right|s_1(z){|}^{\frac{(\frac{k}{2}+1)(1-\rho )Re\eta }{2-\beta }}d\theta )}^{\frac{2-\beta }{2}}{\left(\frac{1+3r^2}{1-r^2}\right)}^{\frac{\beta }{2}}\\ \le & \frac{2^{(\frac{k}{2}-1)(1-\rho )Re\eta +\frac{\beta }{2}}}{r^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -1}}{\left(\frac{1}{1-r}\right)}^{\frac{\beta }{2}}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }\frac{r^{\frac{(\frac{k}{2}+1)(1-\rho )Re\eta }{2-\beta }}}{|1+r{e}^{i\theta }{|}^{\frac{(k+2)(1-\rho )Re\eta }{2-\beta }}}d\theta \right)}^{\frac{2-\beta }{2}}\\ \le & \frac{2^{(\frac{k}{2}-1)(1-\rho )Re\eta +\frac{\beta }{2}}}{r^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -1-\frac{(\frac{k}{2}+1)(1-\rho )Re\eta }{2-\beta }}}{\left(\frac{1}{1-r}\right)}^{\frac{\beta }{2}}{\left(\frac{1}{2\pi }{\int }_0^{2\pi }\frac{1}{|1+r{e}^{i\theta }{|}^{\frac{(k+2)(1-\rho )Re\eta }{2-\beta }}}d\theta \right)}^{\frac{2-\beta }{2}}\\ \le & c(k,\eta ,\rho ,\beta ){\left(\frac{1}{1-r}\right)}^{\frac{\beta }{2}}{\left(\frac{1}{1-r}\right)}^{(\frac{k}{2}+1)(1-\rho )Re\eta +\beta -1}.\end{array}$$

The function $F_0\in \widetilde{N_k}(\eta ,\rho ,\beta )$ defined by

$$F_0^{\mathrm{\prime }}(z)=G_0^{\mathrm{\prime }}(z)h_0^{\beta }(z),$$

(2.5)

where

$$G_0^{\mathrm{\prime }}(z)=\frac{{(1+z)}^{(\frac{k}{2}-1)(1-\rho )\eta }}{{(1-z)}^{(\frac{k}{2}+1)(1-\rho )\eta }}\text{and}{h}_0(z)=\frac{1+z}{1-z},$$

shows that the exponent is sharp. □

By assigning different values to the parameters involved in the above theorem, we have the following interesting results.

Corollary 2.1 Let $f\in \widetilde{T_k}(\rho ,\beta )$. Then

$$L_r(f)\le c(k,\rho ,\beta ){\left(\frac{1}{1-r}\right)}^{(\frac{k}{2}+1)(1-\rho )+\beta -1}.$$

Corollary 2.2 Let $f\in T_k$. Then

$$L_r(f)\le c(k,\rho ,\beta ){\left(\frac{1}{1-r}\right)}^{\frac{k}{2}+1}.$$

Coefficient growth problems The problem of growth rate and asymptotic behavior of coefficients is well known. In the upcoming results, we investigate these problems for a different set of classes by varying different parameters.

Theorem 2.4 Let $f\in \widetilde{N_k}(\eta ,\rho ,\beta )$ and be of the form (1.1). Then, for $n>3$, $k\ge 2$, $Re\eta >0$, $0\le \rho <1$, $\beta \ge 0$, we have

$$|a_n|\le c(k,\eta ,\rho ,\beta )n^{(\frac{k}{2}+1)(1-\rho )Re\eta +\beta -2},$$

where $c(k,\eta ,\rho ,\beta )$ is a constant depending only on k, η, ρ, β. The exponent $[(\frac{k}{2}+1)(1-\rho )Re\eta +\beta -2]$ is sharp.

Proof With $z=r{e}^{i\theta }$, Cauchy’s theorem gives us

$$n{a}_n=\frac{1}{2\pi r^n}{\int }_0^{2\pi }|z{f}^{\mathrm{\prime }}(z)|d\theta =\frac{1}{2\pi r^n}{L}_r(f),z=r{e}^{i\theta }.$$

Using Theorem 2.3 and putting $r=1-\frac{1}{n}$, we obtain the required result. The sharpness follows from the function $F_0$ defined by the relation (2.5). □

Corollary 2.3 Let $f\in {\tilde{T}}_k(\rho ,\beta )$ and be of the form (1.1). Then, for $n>3$, $k\ge 2$, we have

$$|a_n|=\mathrm{O}(1)n^{(\frac{k}{2}+1)(1-\rho )+\beta -2}.$$

For $\rho =0$, $\beta =1$ in the above corollary, we have the growth rate of coefficients problem for functions in this class $T_k$ and for $k=2$, $\rho =0$, $\beta =1$ gives us the growth rate of coefficient estimates for close-to-convex functions, which is well known.

3 Hankel determinant problem

The Hankel determinant of a function f of the form (1.1) is defined by

$$H_q(n)=\left|\begin{array}{cccc}{a}_n& a_{n+1}& \dots & a_{n+q-1}\\ a_{n+1}& a_{n+2}& \dots & a_{n+q}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n+q-1}& a_{n+q}& \dots & a_{n+2q-2}\end{array}\right|.$$

(3.1)

The growth rate of Hankel determinant $H_q(n)$ as $n\to \mathrm{\infty }$, when f is a member of any class of analytic functions, is well known. Pommerenke [9] proved that when f is an areally mean p-valent function, then for $p\ge 1$,

$$H_q(n)=\mathrm{O}(1)n^{s\sqrt{q}-\frac{q}{2}}\text{as }n\to \mathrm{\infty }$$

and $s=16p^{3/2}$ and where $\mathrm{O}(1)$ depends on p, q, and the function f. In particular, this shows that $H_q(n)\to 0$ as $n\to \mathrm{\infty }$ for large q relative to p. In fact, for $p=1$, $q=2$

$$H_2(n)=\mathrm{O}(1)n^{\frac{1}{2}}\text{as }n\to \mathrm{\infty }.$$

The exponent $\frac{1}{2}$ is exact.

Noonan and Thomas [10] gave the exact growth rate of $H_q(n)$ for large p relative to q, and they proved that

$$H_q(n)=\mathrm{O}(1)\{\begin{array}{cc}{n}^{2p-1},\hfill & q=1,p>\frac{1}{4},\hfill \\ n^{2pq-q^2},\hfill & q\ge 2,p\ge 2(q-1),\hfill \end{array}$$

where $\mathrm{O}(1)$ depends upon p, q only and the exponent $2pq-q^2$ is best possible. Also, for univalent functions, Pommerenke [5] has proved that for $q\ge 2$,

$$H_q(n)<c(q)n^{-(\frac{1}{2}+\beta )q+\frac{3}{2}}(n\to \mathrm{\infty }),$$

where $\beta >\frac{1}{4000}$, which in particular shows that

$$H_2(n)<c{n}^{\frac{1}{2}-2\beta }.$$

Pommerenke [9] has shown that if f is starlike, then for $q\ge 1$,

$$H_q(n)=\mathrm{O}(1)n^{2-q}(n\to \mathrm{\infty }),$$

where $\mathrm{O}(1)$ depends upon q only and the exponent $2-q$ is best possible. Noor [11] generalized this result for close-to-convex functions. We also refer to [4, 12–14].

Also, for $f\in V_k$, it is shown [15] that for $q\ge 1$, $n\to \mathrm{\infty }$,

$$H_q(n)=\mathrm{O}(1)\{\begin{array}{cc}{n}^{\frac{k}{2}-1},\hfill & q=1,\hfill \\ n^{\frac{kq}{2}-q^2},\hfill & q\ge 2,k\ge 8q-10,\hfill \end{array}$$

where $\mathrm{O}(1)$ depends upon p, q and f only. The exponent $\frac{kq}{2}-q^2$ is best possible.

Following the notation of Noonan and Thomas [10], we define the following.

Definition 3.1 Let $z_1$ be a non-zero complex number. Then for $f(z)$, given by (1.1), we define

$${\mathrm{\Delta }}_j(n,z_1,f(z))={\mathrm{\Delta }}_{j-1}(n,z_1,f(z))-z_1{\mathrm{\Delta }}_{j-1}(n+1,z_1,f(z)),j\ge 1$$

with ${\mathrm{\Delta }}_1(n,z_1,f(z))=a_n$.

The following two lemmas are due to Noonan and Thomas [10] which are essential in our investigations.

Lemma 3.1 Let $f\in A$ and let the Hankel determinant of f be defined by (3.1). Then, writing ${\mathrm{\Delta }}_j={\mathrm{\Delta }}_j(n,z_1,f)$, we have

$$H_q(n)=\left|\begin{array}{cccc}{\mathrm{\Delta }}_{2q-2}(n)& {\mathrm{\Delta }}_{2q-3}(n+1)& \cdots & {\mathrm{\Delta }}_{q-1}(n+q-1)\\ {\mathrm{\Delta }}_{2q-3}(n+1)& {\mathrm{\Delta }}_{2q-4}(n+2)& \cdots & {\mathrm{\Delta }}_{q-2}(n+q)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathrm{\Delta }}_{q-1}(n+q-1)& {\mathrm{\Delta }}_{q-2}(n+q)& \cdots & {\mathrm{\Delta }}_0(n+2q-2)\end{array}\right|.$$

(3.2)

Lemma 3.2 With $z_1=\frac{n}{n+1}y$ and $v\ge 0$ any integer,

$${\mathrm{\Delta }}_j(n+v,z_1,z{f}^{\mathrm{\prime }})=\sum _{l=0}^j\left(\genfrac{}{}{0ex}{}{j}{l}\right)\frac{y^l(v-(l-1)n)}{{(n+1)}^l}{\mathrm{\Delta }}_{j-l}(n+v+l,y,f).$$

We also need the following remark given in [10].

Remark 3.1 Consider any determinant of the form

$$D=\left|\begin{array}{cccc}{y}_{2q-2}& y_{2q-3}& \cdots & y_{q-1}\\ y_{2q-3}& y_{2q-4}& \cdots & y_{q-2}\\ ⋮& ⋮& ⋮& ⋮\\ y_{q-1}& y_{q-2}& \cdots & y_0\end{array}\right|,$$

with $1\le i$, $j\le q$ and ${\alpha }_{i,j}=y_{2q-(i+j)}$, $D=det({\alpha }_{i,j})$. Thus,

$$D=\sum _{v_1\in S_q}(sgn{v}_1)\prod _{j=1}^q{y}_{2q-(v_1(j)+j)},$$

where $S_q$ is the symmetric group on q elements, and $sgn{v}_1$ is either +1 or −1. Thus, in the expansion of D, each summand has q factors, and the sum of the subscripts of the factors of each summand is $q^2-q$.

Now, let n be given and $H_q(n)$ be as in Lemma 3.1, then each summand in the expansion of $H_q(n)$ is of the form

$$\prod _{i=1}^q{\mathrm{\Delta }}_{v_1(i)}(n+2q-2-v_1(i)),$$

where $v_1\in S_q$ and

$$\sum _{i=1}^q{v}_1(i)=q^2-q;0\le v_1(i)\le 2q-2.$$

We now prove the following.

Theorem 3.1 Let $f\in {\tilde{N}}_k(\eta ,\rho ,\beta )$ and let the Hankel determinant of f, for $q\ge 2$, $n\ge 1$, be defined by (3.1). Then, for $q\ge 2$ and $k>4\frac{(q-1)}{(1-\rho )Re\eta }-2$, we have

$$H_q(n)=\mathrm{O}(1)n^{[(\frac{k}{2}+1)(1-\rho )Re\eta ]q-q^2-(n+1)q},$$

where $\mathrm{O}(1)$ depends only on k, η, ρ, β and q.

Proof Since $f\in {\tilde{N}}_k(\eta ,\rho ,\beta )$, there exists $g\in V_k(\eta ,\rho )$ such that

$$f^{\mathrm{\prime }}(z)=g(z)h^{\beta }(z)\in P,z\in E.$$

Now, for $j\ge 1$, $z_1$ any non-zero complex number and $z=r{e}^{i\theta }$, we consider for $F(z)=z{f}^{\mathrm{\prime }}(z)$,

where we have used Lemma 1.1(iii). Using Lemma 1.3, we have

$$|{\mathrm{\Delta }}_j(n,z_1,F)|\le \frac{1}{2\pi r^{n+j}}{\left(\frac{2r^2}{1-r^2}\right)}^j{\int }_0^{2\pi }\frac{|s_1(z){|}^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -j}}{|s_2(z){|}^{(\frac{k}{4}-\frac{1}{2})(1-\rho )Re\eta }}|h(z){|}^{\beta }d\theta .$$

(3.3)

By employing distortion results for starlike functions and simplifying, we obtain, from (3.3),

$$|{\mathrm{\Delta }}_j(n,z_1,F)|\le \frac{1}{2\pi }\frac{{(2)}^{(\frac{k}{2}-1)(1-\rho )Re\eta }}{r^{(\frac{k}{4}-\frac{1}{2})(1-\rho )Re\eta +n-j-1}}{\left(\frac{1}{1-r}\right)}^j{\int }_0^{2\pi }|s_1(z){|}^{(\frac{k}{4}+\frac{1}{2})(1-\rho )Re\eta -j}|h(z){|}^{\beta }d\theta .$$

Using Holder’s inequality, with $p=\frac{2}{2-\beta }$, $q=\frac{2}{\beta }$, such that $\frac{1}{p}+\frac{1}{q}=1$, we can write

$$\begin{array}{rcl}|{\mathrm{\Delta }}_j(n,z_1,F)|& \le & \frac{{(2)}^{(\frac{k}{2}-1)(1-\rho )Re\eta }}{r^{(\frac{k}{4}-\frac{1}{2})(1-\rho )Re\eta +n-j-1}}{\left(\frac{1}{1-r}\right)}^j{\left(\frac{1}{2\pi }{\int }_0^{2\pi }\right|s_1(z){|}^{\frac{(\frac{k}{2}+1)(1-\rho )Re\eta -2j}{2-\beta }})}^{\frac{2-\beta }{2}}\\ \times {\left(\frac{1}{2\pi }{\int }_0^{2\pi }\right|h(z){|}^{2}d\theta )}^{\frac{\beta }{2}}.\end{array}$$

Proceeding in a similar way as in Theorem 2.3, we have

$$\begin{array}{rcl}|{\mathrm{\Delta }}_j(n,z_1,F)|& \le & \frac{{(2)}^{(\frac{k}{2}-1)(1-\rho )Re\eta +\frac{\beta }{2}}}{r^{n-1}}{\left(\frac{1}{1-r}\right)}^{\frac{\beta }{2}+j}\\ \times {\left(\frac{1}{2\pi }{\int }_0^{2\pi }\frac{1}{|1-r{e}^{i\theta }{|}^{\frac{(k+2)(1-\rho )Re\eta -4j}{2-\beta }}}d\theta \right)}^{\frac{2-\beta }{2}}.\end{array}$$

Subordination for starlike functions further yields

$$|{\mathrm{\Delta }}_j(n,z_1,F)|=\mathrm{O}(1){\left(\frac{1}{1-r}\right)}^{(\frac{k}{2}+1)(1-\rho )Re\eta -j+\beta -1},$$

where $\mathrm{O}(1)$ depends only on k, η, β and j.

Now, applying Lemma 3.2 and putting $z_1=\frac{n}{n+1}{e}^{i{\theta }_m}$ ($n\to \mathrm{\infty }$), we have for $k\ge (\frac{4j}{(1-\rho )Re\eta }-2)$, $j\ge 1$,

$${\mathrm{\Delta }}_j(n,e^{i{\theta }_n},f(z))=\mathrm{O}(1)n^{(\frac{k}{2}+1)(1-\rho )Re\eta -j+\beta -1}.$$

We now estimate the growth rate of $H_q(n)$. For $q=1$, $H_q(n)=a_n={\mathrm{\Delta }}_0(n)$ and from Theorem 2.4, it follows that

$$H_1(n)=\mathrm{O}(1)n^{(\frac{k}{2}+1)(1-\rho )Re\eta +\beta -2}.$$

For $q\ge 2$, we use Remark 3.1 together with Lemma 3.1, to have

$$H_q(n)=\mathrm{O}(1)n^{q[(\frac{k}{2}+1)(1-\rho )Re\eta +\beta ]-q^2},k>(\frac{4(q-1)}{(1-\rho )Re\eta }-2),$$

where $\mathrm{O}(1)$ depends only on k, η, ρ, β and q. □

By giving special values to the parameters involved in the above theorem, we obtain the following interesting results.

Corollary 3.1 Let $f\in {\tilde{T}}_k(\rho ,\beta )$ and be defined as in (1.1). Then, for $q\ge 2$, $k>(\frac{4(q-1)}{1-\rho }-2)$,

$$H_q(n)=\mathrm{O}(1)n^{q[(\frac{k}{2}+1)(1-\rho )+\beta ]-q^2}(n\to \mathrm{\infty }),$$

where $\mathrm{O}(1)$ depends only on k, ρ, β and q.

Noor [4] studied the above corollary with a different method.

Corollary 3.2 Let $f\in T_k$ and be defined as in (1.1). Then, for $q\ge 2$, $k>(4q-6)$,

$$H_q(n)=\mathrm{O}(1)n^{q[(\frac{k}{2}+2]-q^2}(n\to \mathrm{\infty }),$$

where $\mathrm{O}(1)$ depends only on k and q.