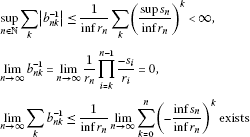Abstract
Let λ denote any one of the classical spaces , c, and of bounded, convergent, null and absolutely p-summable sequences, respectively, and also be the domain of the double sequential band matrix in the sequence space λ, where and are given convergent sequences of positive real numbers and . The present paper is devoted to studying the sequence space . Furthermore, the β- and γ-duals of the space are determined, the Schauder bases for the spaces , and are given, and some topological properties of the spaces , and are examined. Finally, the classes and of infinite matrices are characterized, where and .
MSC:46A45, 40C05.
Similar content being viewed by others
1 Preliminaries, background and notation
By a sequence space, we understand a linear subspace of the space of all complex sequences which contains ϕ, the set of all finitely non-zero sequences, where ℂ denotes the complex field and . We write , c, and for the classical sequence spaces of all bounded, convergent, null and absolutely p-summable sequences, respectively, where . Also, by bs and cs, we denote the spaces of all bounded and convergent series, respectively. bv is the space consisting of all sequences such that in and is the intersection of the spaces bv and . We assume throughout, unless stated otherwise, that with and use the convention that any term with a negative subscript is equal to naught.
Let be an infinite matrix of complex numbers , where , and write
where denotes the subspace of ω consisting of for which the sum exists as a finite sum. For simplicity in notation, here and in what follows, the summation without limits runs from 0 to ∞. More generally if μ is a normed sequence space, we can write for , for which the sum in (1.1) converges in the norm of μ. We write
for the space of those matrices which send the whole of the sequence space λ into the sequence space μ in this sense.
A matrix is called a triangle if for and for all . It is trivial that holds for the triangle matrices A, B and a sequence x. Further, a triangle matrix U uniquely has an inverse which is also a triangle matrix. Then holds for all .
Let us give the definition of some triangle limitation matrices which are needed in the text. Let be a sequence of positive reals and write
Then the Cesáro mean of order one, Riesz mean with respect to the sequence and Euler mean of order r are respectively defined by the matrices , and , where
and
for all . We write for the set of all sequences such that for all . For , let . Let and define the summation matrix , the difference matrix , the generalized weighted mean or factorable matrix , , and by

for all , where depends only on n and only on k.
Let and define the generalized difference matrix by
for all . We should record here that the matrix can be reduced to the difference matrix in case , . So, the results related to the matrix domain of the matrix are more general and more comprehensive than the corresponding consequences of the matrix domain of and include them.
The domain of an infinite matrix A in a sequence space λ is defined by
which is a sequence space. If A is triangle, then one can easily observe that the sequence spaces and λ are linearly isomorphic, i.e., . If λ is a sequence space, then the continuous dual of the space is defined by
Although in most cases the new sequence space generated by the limitation matrix A from a sequence space λ is the expansion or the contraction of the original space λ, it may be observed in some cases that those spaces overlap. Indeed, one can easily see that the inclusion strictly holds for . Similarly, one can deduce that the inclusion also strictly holds for . However, if we define with , i.e., if and only if for some and some , and consider the matrix A with the rows defined by for all , we have but which lead us to the consequences that and , where and is a sequence whose only non-zero term is a 1 in n th place for each . That is to say, the sequence spaces and λ overlap but neither contains the other. The approach of constructing a new sequence space by means of the matrix domain of a particular limitation method has recently been employed by Wang [1], Ng and Lee [2], Malkowsky [4], Altay and Başar [10, 20, 36, 37, 41, 46], Malkowsky and Savaş [8], Başarır [47], Aydın and Başar [12, 13, 16, 30, 39], Başar et al. [38], Şengönül and Başar [9], Altay [23], Polat and Başar [25] and Malkowsky et al. [43]. In Table 1, Δ, and are the transpose of the matrices , and , respectively, and and are the spaces consisting of the sequences such that in the spaces and for , respectively, and studied by Başarır [47]. Finally, the new technique for deducing certain topological properties, for example AB-, KB-, AD-properties, solidity and monotonicity etc., and determining the β- and γ-duals of the domain of a triangle matrix in a sequence space is given by Altay and Başar [46].
Let and be given convergent sequences of positive real numbers. Define the sequential generalized difference matrix by
for all , the set of natural numbers. We should record here that the matrix can be reduced to the generalized difference matrix in the case and for all . So, the results related to the matrix domain of the matrix are more general and more comprehensive than the corresponding consequences of the matrix domain of and include them. For the literature concerning the domain of the infinite matrix A in the sequence space λ, Table 1 may be useful.
The main purpose of the present paper is to introduce the sequence space and to determine the β- and γ-duals of the space, where λ denotes any one of the spaces , c, or . Furthermore, the Schauder bases for the spaces , and are given and some topological properties of the spaces , and are examined. Finally, some classes of matrix mappings on the space are characterized.
The paper is organized as follows. In Section 2, we summarize the studies on the difference sequence spaces. In Section 3, we introduce the domain of the generalized difference matrix in the sequence space λ with and determine the β- and γ-duals of . After proving the fact, under which conditions for the inclusion and the equality hold, we give the Schauder basis of the spaces , and . Finally, we investigate some topological properties of the spaces , and with . In Section 4, we state and prove a general theorem characterizing the matrix transformations from the domain of a triangle matrix to any sequence space. As an application of this basic theorem, we make a table which gives the necessary and sufficient conditions of the matrix transformations from to μ, where and . In the final section of the paper, we note the significance of the present results in the literature about difference sequences and record some further suggestions.
2 Difference sequence spaces
In this section, we give some knowledge about the literature concerning the spaces of difference sequences.
Let λ denote any one of the classical sequence spaces , c or . Then consisting of the sequences such that is called the difference sequence spaces which were introduced by Kızmaz [5]. Kızmaz [5] proved that is a Banach space with the norm
and the inclusion relation strictly holds. He also determined the α-, β- and γ-duals of the difference spaces and characterized the classes and of infinite matrices, where . Following Kızmaz [5], Sarıgöl [48] extended the difference spaces to the spaces defined by
and computed the α-, β-, γ-duals of the space , where . It is easily seen that , if and , if .
In the same year, Ahmad and Mursaleen [33] extended these spaces to and studied related problems. Malkowsky [49] determined the Köthe-Toeplitz duals of the sets and and gave new proofs of the characterization of the matrix transformations considered in [33]. In 1993, Choudhary and Mishra [50] studied some properties of the sequence space for . In the same year, Mishra [51] gave a characterization of BK-spaces which contain a subspace isomorphic to in terms of matrix maps and a sufficient condition for a matrix map from into a BK-space to be a compact operator. He showed that any matrix from into a BK-space which does not contain any subspace isomorphic to is compact, where
In 1996, Mursaleen et al. [52] defined and studied the sequence space
Gnanaseelan and Srivastava [53] defined and studied the spaces for a sequence of non-complex numbers such that
-
(i)
for each .
-
(ii)
.
-
(iii)
is a sequence of positive numbers increasing monotonically to infinity.
In the same year, Malkowsky [54] defined the spaces for an arbitrary fixed sequence without any restrictions on u. He proved that the sequence spaces are BK-spaces with the norm defined by
Later, Gaur and Mursaleen [55] extended the space to the space , where
and characterized the matrix classes and . Malkowsky et al. [56] and, independently, Asma and Çolak [34] extended the space to the space and gave Köthe-Toeplitz duals of this spaces for , c or . Recently, Malkowsky and Mursaleen [57] characterized the matrix classes and for , , and , , .
Recently, the difference spaces consisting of the sequences such that have been studied in the case by Altay and Başar [20], and in the case by Başar and Altay [18] and Çolak et al. [19].
3 Some new sequence spaces derived by the domain of the matrix
In this section, we define the sequence spaces , , and , and determine the β- and γ-duals of the spaces.
We introduce the sequence spaces , , and as the set of all sequences whose -transforms are in the spaces , c, and , respectively, that is,

With the notation of (1.2), we can redefine the spaces , , and by
Define the sequence by the -transform of a sequence , i.e.,
Since the spaces λ and are linearly isomorphic, one can easily observe that if and only if , where the sequences and are connected with the relation (3.1).
Prior to quoting the lemmas which are needed for deriving some consequences given in Corollary 3.4 below, we give an inclusion theorem related to these new spaces.
Theorem 3.1 Let and . Then
-
(i)
, if .
-
(ii)
is strict, if .
Proof Let and . Since the matrix B satisfies the conditions

and
. For any sequence , hence . This shows that .
-
(i)
Let . Since the inverse matrix of the matrix B also satisfies the conditions
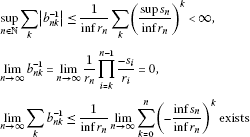
and
. Therefore, if , then and . Thus, the opposite inclusion is just proved. This completes the proof of Part (i).
-
(ii)
Let us consider the sequences , and .
If , then . Hence, .
Suppose that .
-
(a)
Let . If , then .
-
(b)
Let . If , then , . Hence, and .
This step completes the proof. □
The set defined by
is called the multiplier space of the spaces λ and μ. One can easily observe for a sequence space ν with that the inclusions
hold. With the notation of (3.2), the α-, β- and γ-duals of a sequence space λ, which are respectively denoted by , and , are defined by
Lemma 3.2 [[58], p.52, Exercise 2.5(i)]
Let λ, μ be the sequence spaces and . If , then .
We read the following useful results from Stieglitz and Tietz [59]:





Lemma 3.3 The necessary and sufficient conditions for when and can be read from Table 2.
Basic Lemma [[46], Theorem 3.1]
Let be defined via the sequence and the inverse matrix of the triangle matrix by
for all . Then
and
Combining Lemma 3.3 with Basic Lemma, we have
Corollary 3.4 Define the sets , , , and by

and
Then
-
(i)
with .
-
(ii)
.
-
(iii)
.
-
(iv)
.
-
(v)
with .
-
(vi)
with .
-
(vii)
.
-
(viii)
.
A sequence space λ with a linear topology is called a K-space provided each of the maps defined by is continuous for all . A K-space λ is called an FK-space provided λ is a complete linear metric space. An FK-space whose topology is normable is called a BK-space. If a normed sequence space λ contains a sequence with the property that for every , there is a unique sequence of scalars such that
then is called a Schauder basis (or briefly basis) for λ. The series which has the sum x is then called the expansion of x with respect to and written as .
Since it is known that the matrix domain of a normed sequence space λ has a basis if and only if λ has a basis whenever is a triangle (cf. [[60], Remark 2.4]), we have
Corollary 3.5 Define the sequences and for every fixed by
Then
-
(a)
the sequence is a basis for the spaces and , and any x in or in has a unique representation of the form
where for all .
-
(b)
the set is a basis for the space , and any x in has a unique representation of the form
where .
By λμ, we mean the set
for the sequence spaces λ and μ.
Given a BK-space , we denote the n th section of a sequence by , and we say that x has the property
AK if (abschnittskonvergenz),
AB if (abschnittsbeschränktheit),
AD if (closure of ) (abschnittsdichte),
KB if the set is bounded in λ (koordinatenweise beschränkt).
If one of these properties holds for every , then we say that the space λ has that property (cf. [61]). It is trivial that AK implies AD and AK iff AB and AD. For example, and are AK-spaces and c and are not AD-spaces.
The sequence space λ is said to be solid if and only if
For a sequence J of ℕ and a sequence space λ, we define by
and call the J-stepspace or a J-sectional subspace of λ. If , then the canonical preimage of is the sequence which agrees with on the indices in J and is zero elsewhere. Then λ is called monotone provided λ contains the canonical preimages of all its stepspaces.
Lemma 3.6 [[46], Theorem 2.1 and Lemma 4.1]
Let λ, μ be the BK-spaces and be defined via the sequence and the triangle matrix by
for all . Then the domain of the matrix U in the sequence space λ has the property
-
(i)
KB if and only if ,
-
(ii)
AB if and only if ,
-
(iii)
monotone if and only if ,
-
(iv)
solid if and only if .
From Lemma 3.6, we have
Corollary 3.7 If for all , then has the KB- and AB-properties.
Lemma 3.8 [[46], Theorem 2.2]
Let λ be a BK-space which has the AK-property, U be a triangle matrix and . Then the sequence space has the AD-property if and only if the fact for implies the fact .
Since and have the AK-property, we can employ Lemma 3.8 for the matrix . Then we have
Corollary 3.9 and () have the AD-property if and only if for all .
4 Some matrix transformations related to the sequence spaces , , and
In the present section, we characterize some classes of infinite matrices related to new sequence spaces.
Theorem 4.1 Let λ be an FK-space, U be a triangle, V be its inverse and μ be an arbitrary subset of ω. Then we have if and only if
and
where
Proof Let and take . Then we obtain the equality
for all . Since Ax exists, must belong to the class . Letting in equality (4.3) we have . Since , then , i.e., .
Conversely, let (4.1), (4.2) hold and take . Then we have , which together with (4.1) gives that for all . Hence, Ax exists. Therefore, we obtain from equality (4.3) as that and this shows that . □
Now, we list the following conditions:














where ℱ denotes the collection of all finite subsets of ℕ.
We have from Theorem 4.1
Corollary 4.2 The necessary and sufficient conditions for when and can be read from Table 3.
Now, we may present our final lemma given by Başar and Altay [[18], Lemma 5.3] which is useful for obtaining the characterization of some new matrix classes from Corollary 4.2.
Lemma 4.3 Let λ, μ be any two sequence spaces, A be an infinite matrix and U be a triangle matrix. Then if and only if .
We should finally note that if is replaced by for all in Corollary 4.2, then one can derive the characterization of the class from Lemma 4.3 with .
5 Conclusion
Quite recently, Kirişçi and Başar [44] studied the domain of the generalized difference matrix in the classical sequence spaces , c, and . Later, Sönmez [45] generalized these results by using the triple band matrix . Since the generalized difference matrix is obtained in the special case and for all from the double sequential band matrix , our results are much more general than the corresponding results given by Kirişçi and Başar [44].
Finally, we should note that our next paper will be devoted to the investigation of the domain of the double sequential band matrix in the space f of almost convergent sequences introduced by Lorentz in [62] which generalizes the corresponding results of Başar and Kirişçi [63].
References
Wang C-S: On Nörlund sequence spaces. Tamkang J. Math. 1978, 9: 269–274.
Ng P-N, Lee P-Y: Cesàro sequence spaces of non-absolute type. Ann. Soc. Math. Pol., 1 Comment. Math. 1978, 20(2):429–433.
Et M: On some generalized Cesàro difference sequence spaces. Istanb. Üniv. Fen Fak. Mat. Derg. 1996–1997, 55–56: 221–229.
Malkowsky E: Recent results in the theory of matrix transformations in the sequence spaces. Mat. Vesn. 1997, 49: 187–196.
Kızmaz H: On certain sequence spaces. Can. Math. Bull. 1981, 24(2):169–176. 10.4153/CMB-1981-027-5
Et M: On some difference sequence spaces. Turk. J. Math. 1993, 17: 18–24.
Mursaleen M: Generalized spaces of difference sequences. J. Math. Anal. Appl. 1996, 203(3):738–745. 10.1006/jmaa.1996.0409
Malkowsky E, Savaş E: Matrix transformations between sequence spaces of generalized weighted means. Appl. Math. Comput. 2004, 147: 333–345. 10.1016/S0096-3003(02)00670-7
Şengönül M, Başar F: Some new Cesàro sequence spaces of non-absolute type which include the spaces and c . Soochow J. Math. 2005, 31(1):107–119.
Altay B, Başar F: Some Euler sequence spaces of non-absolute type. Ukr. Math. J. 2005, 57(1):1–17. 10.1007/s11253-005-0168-9
Rhoades BE: Some sequence spaces which include and c . Hokkaido Math. J. 2006, 35: 587–599.
Aydın C, Başar F: On the new sequence spaces which include the spaces and c . Hokkaido Math. J. 2004, 33(2):383–398.
Aydın C, Başar F:Some new sequence spaces which include the spaces and . Demonstr. Math. 2005, 38(3):641–656.
Altay B, Başar F, Mursaleen M:On the Euler sequence spaces which include the spaces and I. Inf. Sci. 2006, 176(10):1450–1462. 10.1016/j.ins.2005.05.008
Mursaleen M, Başar F, Altay B:On the Euler sequence spaces which include the spaces and II. Nonlinear Anal. TMA 2006, 65(3):707–717. 10.1016/j.na.2005.09.038
Aydın C, Başar F: Some new difference sequence spaces. Appl. Math. Comput. 2004, 157(3):677–693. 10.1016/j.amc.2003.08.055
Khan FM, Rahman MF: Matrix transformations on Cesà ro sequence spaces of nonabsolute type. J. Anal. 1996, 4: 97–101.
Başar F, Altay B: On the space of sequences of p-bounded variation and related matrix mappings. Ukr. Math. J. 2003, 55(1):136–147. 10.1023/A:1025080820961
Çolak R, Et M, Malkowsky E Lecture Notes in Mathematics. In Some Topics of Sequence Spaces. Fırat Univ. Press, Elazığ; 2004. ISBN:975–394–0386–6
Altay B, Başar F:The matrix domain and the fine spectrum of the difference operator Δ on the sequence space , (). Commun. Math. Anal. 2007, 2(2):1–11.
Et M, Çolak R: On some generalized difference sequence spaces. Soochow J. Math. 1995, 21(4):377–386.
Çolak R, Et M: On some generalized sequence spaces and related matrix transformations. Hokkaido Math. J. 1997, 26(3):483–492.
Altay B: On the space of p -summable difference sequences of order m , ( ). Studia Sci. Math. Hung. 2006, 43(4):387–402.
Malkowsky E, Parashar SD: Matrix transformations in space of bounded and convergent difference sequence of order m . Analysis 1997, 17: 87–97.
Polat H, Başar F: Some Euler spaces of difference sequences of order m . Acta Math. Sci. 2007, 27(2):254–266.
Altay B, Başar F, Malkowsky E: Matrix transformations on some sequence spaces related to strong Cesàro summability and boundedness. Appl. Math. Comput. 2009, 211: 255–264. 10.1016/j.amc.2009.01.062
Başar F, Malkowsky E, Altay B:Matrix transformations on the matrix domains of triangles in the spaces of strongly -summable and bounded sequences. Publ. Math. 2008, 73(1–2):193–213.
Başar F: Infinite matrices and almost boundedness. Boll. Unione Mat. Ital., A 1992, 6(3):395–402.
Başar F, Altay B: Matrix mappings on the space and its α -, β - and γ -duals. Aligarh Bull. Math. 2001, 21(1):79–91.
Aydın C, Başar F:Some generalizations of the sequence space . Iran. J. Sci. Technol., Trans. A, Sci. 2006, 30(A2):175–190.
Aydın, C, Başar, F: Some topological and geometric properties of the domain of the generalized difference matrix in the sequence spaces . Serbia, June 2009, Book of Abstracts p.p. 1
Choudhary B, Mishra SK: On Köthe-Toeplitz duals of certain sequence spaces and their matrix transformations. Indian J. Pure Appl. Math. 1993, 24(5):291–301.
Ahmad ZU, Mursaleen M: Köthe-Toeplitz duals of some new sequence spaces and their matrix maps. Publ. Inst. Math. (Belgr.) 1987, 42: 57–61.
Asma Ç, Çolak R: On the Köthe-Toeplitz duals of some generalized sets of difference sequences. Demonstr. Math. 2000, 33: 797–803.
Bektaş ÇA: On some new generalized sequence spaces. J. Math. Anal. Appl. 2003, 277: 681–688. 10.1016/S0022-247X(02)00619-4
Altay B, Başar F: Some paranormed sequence spaces of non-absolute type derived by weighted mean. J. Math. Anal. Appl. 2006, 319(2):494–508. 10.1016/j.jmaa.2005.06.055
Altay B, Başar F:Generalization of the sequence space derived by weighted mean. J. Math. Anal. Appl. 2007, 330(1):174–185. 10.1016/j.jmaa.2006.07.050
Başar F, Altay B, Mursaleen M:Some generalizations of the space of p-bounded variation sequences. Nonlinear Anal. 2008, 68(2):273–287. 10.1016/j.na.2006.10.047
Aydın C, Başar F: Some new paranormed sequence spaces. Inf. Sci. 2004, 160(1–4):27–40. 10.1016/j.ins.2003.07.009
Altay B, Başar F: On the paranormed Riesz sequence spaces of non-absolute type. Southeast Asian Bull. Math. 2002, 26(5):701–715.
Altay B, Başar F: Some paranormed Riezs sequence spaces of non-absolute type. Southeast Asian Bull. Math. 2006, 30(5):591–608.
Et M, Başarır M: On some new generalized difference sequence spaces. Period. Math.-Phys 1987, 10: 63–71.
Malkowsky E, Mursaleen M, Suantai S: The dual spaces of sets of difference sequences of order m and matrix transformations. Acta Math. Sin. Engl. Ser. 2007, 23(3):521–532. 10.1007/s10114-005-0719-x
Kirişçi M, Başar F: Some new sequence spaces derived by the domain of generalized difference matrix. Comput. Math. Appl. 2010, 60(5):1299–1309. 10.1016/j.camwa.2010.06.010
Sönmez A: Some new sequence spaces derived by the domain of the triple band matrix. Comput. Math. Appl. 2011, 62(2):641–650. 10.1016/j.camwa.2011.05.045
Altay B, Başar F: Certain topological properties and duals of the matrix domain of a triangle matrix in a sequence space. J. Math. Anal. Appl. 2007, 336(1):632–645. 10.1016/j.jmaa.2007.03.007
Başarır M: On some new sequence spaces and related matrix transformations. Indian J. Pure Appl. Math. 1995, 26(10):1003–1010.
Sarıgöl MA: On difference sequence spaces. J. Karadeniz Tech. Univ. Fac. Arts Sci. Ser. Math.-Phys. 1987, 10: 63–71.
Malkowsky E: Absolute and ordinary Köthe-Toeplitz duals of some sets of sequences and matrix transformations. Publ. Inst. Math. (Beograd) (N.S.) 1989, 46(60):97–103.
Choudhary B, Mishra SK: A note on certain sequence spaces. J. Anal. 1993, 1: 139–148.
Mishra SK: Matrix maps involving certain sequence spaces. Indian J. Pure Appl. Math. 1993, 24(2):125–132.
Mursaleen M, Gaur AK, Saifi AH: Some new sequence spaces and their duals and matrix transformations. Bull. Calcutta Math. Soc. 1996, 88(3):207–212.
Gnanaseelan C, Srivastava PD: The α -, β - and γ -duals of some generalised difference sequence spaces. Indian J. Math. 1996, 38(2):111–120.
Malkowsky E: A note on the Köthe-Toeplitz duals of generalized sets of bounded and convergent difference sequences. J. Anal. 1996, 4: 81–91.
Gaur AK, Mursaleen M: Difference sequence spaces. Int. J. Math. Math. Sci. 1998, 21(4):701–706. 10.1155/S0161171298000970
Malkowsky E, Mursaleen M, Qamaruddin Q: Generalized sets of difference sequences, their duals and matrix transformations. In Sequence Spaces and Applications. Narosa, New Delhi; 1999:68–83.
Malkowsky E, Mursaleen M:Some matrix transformations between the difference sequence spaces , and . Filomat 2001, 15: 353–363.
Kamthan PK, Gupta M: Sequence Spaces and Series. Dekker, New York; 1981.
Stieglitz M, Tietz H: Matrix transformationen von folgenräumen eine ergebnisübersicht. Math. Z. 1997, 154: 1–16.
Jarrah AM, Malkowsky E: BK spaces, bases and linear operators. Rend. Circ. Mat. Palermo (2) 1990, 52: 177–191.
Grosse-Erdmann K-G:On -invariant sequence spaces. J. Math. Anal. Appl. 2001, 262: 112–132. 10.1006/jmaa.2001.7546
Lorentz GG: A contribution to the theory of divergent sequences. Acta Math. 1948, 80: 167–190. 10.1007/BF02393648
Başar F, Kirişçi M: Almost convergence and generalized difference matrix. Comput. Math. Appl. 2011, 61(3):602–611. 10.1016/j.camwa.2010.12.006
Acknowledgements
The author would like to express their gratitude to professor Bilal Altay, Department of Mathematical Education, İnönü University, 44280 Malatya-Turkey, for making some constructive comments on the main results of the earlier version of the manuscript which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Candan, M. Domain of the double sequential band matrix in the classical sequence spaces. J Inequal Appl 2012, 281 (2012). https://doi.org/10.1186/1029-242X-2012-281
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-281